До этого мы рассматривали только одномерные распределения вероятностей на числовой прямой. Однако ничто не мешает в качестве носителя выбрать пространство более высокой размерности. И снова все представляющие практический интерес распределения делятся на два класса: дискретные и непрерывные.
Дискретные многомерные распределения
Пусть, например, эксперимент состоит из двух фаз: сначала подбрасывается монетка, а затем кубик. Тогда вероятностная масса сосредоточена в точках , , . Вероятность каждого исхода можно записать в виде таблицы
|
«Неудача» |
«Успех» |
|
|
|
|
|

|
|
|

|
|
|

|
|
|

|
|
|
|
|
|
|
Результат подбрасывания монеты моделирует бернуллиевская случайная величина , а результат броска кубика — равномерно распределённая на множестве случайная величина . Содержимое таблицы вероятностей каждого исхода можно также представить матрицей
которая задаёт совместное распределение случайных величин и : . Пару случайных величин в таком контексте называют также случайным вектором.
Элементы матрицы не обязаны совпадать; например, монета может быть несимметричной с вероятностью «успеха» , и тогда таблица вероятностей примет вид
|
«Неудача» |
«Успех» |
|
|
|
|
|

|
|
|

|
|
|

|
|
|

|
|
|
|
|
|
|
Контрольный вопрос. Какая таблица вероятностей соответствует эксперименту, в котором результат подбрасывания монеты «портит» кубик следующим образом: на нём могут равновероятно выпасть только значения или в случае «неудачи» и , или в случае «успеха»?
Ответ
|
«Неудача» |
«Успех» |
|
|
|
|
|

|
|
|

|
|
|

|
|
|

|
|
|
|
|
|
|
В общем случае дискретное -мерное распределение задаётся многомерным тензором из неотрицательных чисел , суммирующихся в единицу. Такие тензоры используются для задания совместного распределения вероятностей случайного вектора из дискретных случайных величин:
Непрерывные многомерные распределения
Непрерывное распределение на плоскости задаётся плотностью ; при этом вероятность события равна
при условии, что этот интеграл имеет смысл. Простейший пример — равномерное распределение на единичном квадрате : его плотность равна , и
Именно так на единичном квадрате формально определяется геометрическая вероятность.
Плотность непрерывного распределения в является неотрицательной функцией вида со свойством
Говорят, что случайный вектор имеет совместную плотность , если
для всех достаточно «хороших» (измеримых по Лебегу) множеств .
Маргинальные распределения
Из совместного распределения можно получить распределение в пространстве меньшей размерности путём суммирования или интегрирования по части переменных. Например, если матрица задаёт совместное распределение случайных величин и , , то каждый из наборов чисел
неотрицателен и суммируется в единицу:
Таким образом, числа и задают некоторые распределения вероятностей, называемые маргинальными.
Упражнение. Найдите маргинальные распределения, если совместное распределение задано матрицей
Ответ
Суммируя столбцы этих матриц, получаем вероятности в случае а) и в случае б). Если же суммировать строки, то получаются наборы
Заметим, что в п. а) после маргинализации получились в точности распределения вероятностей компонент случайного вектора из приведённого выше примера. Это следствие независимости случайных величин и .
В непрерывном случае ситуация похожая: если случайный вектор имеет совместную плотность , то функции
являются плотностями маргинальных распределений.
Для -мерных распределений можно находить маргинальные распределения, суммируя или интегрируя по любым наборам переменных с индексами ; в результате получится маргинальное распределение по оставшимся переменным.
Независимость случайных величин
Случайные величины и называются независимыми, если совместное распределение случайного вектора распадается на произведение одномерных. Точнее говоря,
- дискретные случайные величины и независимы, если для всех возможных и ;
- непрерывные случайные величины и независимы, если их совместная плотность
.
Если случайные величины и независимы, то распределение каждой из них является маргинальным распределением их совместного распределения, поскольку
и
Случайные величины независимы в совокупности, если их совместное распределение (совместная плотность) распадается в произведение одномерных распределений (плотностей).
Пример. Рассмотрим гауссовских случайных величин с плотностями
Совместную плотность случайного вектора определим как произведение плотностей его компонент:
Случайный вектор с такой плотностью имеет многомерное нормальное (гауссовское) распределение c независимыми в совокупности компонентами. Любое маргинальное распределение случайного вектора обладает плотностью того же вида, и поэтому также является гауссовским.
Характеристики случайных векторов
Математическое ожидание случайного вектора является вектором той же размерности и вычисляется покомпонентно:
Каждая компонента случайного вектора — это обычная случайная величина, и её среднее можно вычислить стандартными методами:
- в дискретном случае;
- в непрерывном случае.
Математическое ожидание перестановочно с линейным преобразованием случайного вектора: , где — фиксированная матрица.
Вместо дисперсии у случайного вектора есть матрица ковариаций:
Матрица ковариаций симметрична и состоит из попарных ковариаций компонент случайного вектора :
Упражнение. Докажите, что ковариационная матрица любого случайного вектора неотрицательно определена.
Решение (не открывайте сразу, сначала попробуйте решить самостоятельно)
Пользуясь линейностью математического ожидания, получаем
Если случайные величины независимы в совокупности, то , и ковариационая матрица случайного вектора диагональна:
Например, матрица ковариации гауссовского случайного вектора с плотностью
равна , поскольку компоненты вектора независимы в совокупности и имеют нормальное распределение .
Аналогом ковариации в многомерном случае служит матрица ковариаций между случайными векторами и :
Матрицу ковариаций можно также вычислить по формуле
Упражнение. Пусть случайный вектор получен из случайного вектора линейным преобразованием: . Как связаны между собой их ковариационные матрицы?
Решение (не открывайте сразу, сначала попробуйте решить самостоятельно)
Распишем по определению:
Преобразования плотностей случайных векторов
Нередко приходится иметь дело не с самими случайными векторами, а с функциями от них. Но как найти плотность случайного вектора , зная плотность ?
Предположим, что — гладкая обратимая функция. Тогда для измеримого имеем
Чтобы перейти к интегралу по , сделаем замену переменной . По формуле замены координат в кратном интеграле получаем
где – якобиан преобразования , т.е. определитель матрицы Якоби .
Таким образом,
Упражнение. Пусть – случайный вектор с плотностью . Какова плотность случайного вектора , где – постоянный вектор, а – постоянная обратимая матрица?
Решение (не открывайте сразу, сначала попробуйте решить самостоятельно)
В данном случае , . Матрица Якоби преобразования равна . Следовательно,
Распределение суммы независимых случайных величин
В дискретном случае найти распределение суммы двух независимых случайных величин несложно. В самом деле,
В силу независимости случайных величин и последняя сумма равна
Полученная формула называется формулой свёртки.
Пусть теперь и – независимые непрерывные случайные величины с плотностями и соответственно. Сам собой напрашивается аналог формулы свёртки с плотностями вместо вероятностей, но чтобы достаточно строго вывести его и не запутаться, мы немного схитрим. А именно, мы рассмотрим случайный вектор и его (обратимое!) преобразование
Обратное к нему будет иметь вид
Тогда по правилу преобразования плотности
где в последнем равенстве мы воспользовались независимостью и . Распределение случайной величины – это маргинальное распределение, которое вычисляется следующим образом:
Эта формула также называется формулой свёртки.
Примеры многомерных распределений
Рассмотрим несколько популярных распределений случайных векторов.
Мультиномиальное распределение
Биномиальное распределение моделирует -кратное подбрасывание монеты с вероятностями «успеха» и «неудачи» . Мультиномиальное распределение обобщает этот эксперимент: теперь подбрасывается кубик с гранями, и вероятность выпадения -й грани равна , . Обозначим через количество выпадений -й грани в серии из бросков. Тогда случайный вектор имеет мультиномиальное распределение, при котором
При мультиномиальное распределение превращается в категориальное, известное также под названием multinoulli. Категориальное распределение моделирует случайный выбор одного из классов с заданными вероятностями .
Многомерное нормальное распределение
Многомерное нормальное (гауссовское) распределение задаётся функцией плотности
где , — невырожденная симметричная матрица размера . Такое распределение обозначается .
Если случайный вектор , то , ; таким образом, параметры гауссовского распределения — это его среднее и матрица ковариаций.
Упражнение. Пусть и . Докажите, что .
Решение (не открывайте сразу, сначала попробуйте решить самостоятельно)
Если бы нам стало известно, что вектор гауссовский, то мы нашли бы его параметры по стандартным формулам:
Решим задачу честно в предположении, что матрица квадратная и невырожденная. Для этого воспользуемся формулой плотности линейного преобразования случайного вектора:
В полученном выражении нетрудно узнать плотность гауссовского распределения .
Заметим, что утверждение сохраняет силу и для случая прямоугольной матрицы размера , где — размерность случайного вектора .
Важный частный случай случайного гауссовского вектора с независимыми компонентами был рассмотрен в примере из секции про независимость случайных величин. Такое распределение получается, если матрица диагональна, . Тогда , , и поэтому
Отсюда снова получаем формулу совместной плотности
которую можно переписать в виде
откуда следует независимость в совокупности компонент вектора .
Если ковариационная матрица не является диагональной, то отдельные компоненты случайного вектора зависимы. Тем не менее, всегда найдётся линейное (и даже ортогональное) преобразование, которое превратит вектор в гауссовский вектор с независимыми компонентами. Для этого достаточно найти ортогональную матрицу со свойством
и далее воспользоваться формулой плотности линейного преобразования гауссовского вектора.
По тем же соображениям облако точек, сгенерированных из распределения , будет напоминать эллипсоид с полуосями, пропорциональными вектору . Линии уровня плотности задаются уравнениями вида , а такое равенство эквивалентно квадратичной форме
где и – некоторые константы. С помощью описанной выше ортогональной замены эта квадратичная форма может быть приведена к главным осям:
в координатах это выглядит как
Мы получили практически каноническое уравнение -мерного эллипсоида. В это будут эллипсы, сплюснутые тем сильнее, чем дальше от единицы отношение собственных значений матрицы .
Нормальным будет и всякое маргинальное распределение многомерного гауссовского вектора.
Упражнение. Пусть случайный вектор имеет гауссовское распределение с параметрами
где , , , , .
Докажите, что случайный вектор , полученный маргинализацией по компонентам вектора , является гауссовским с параметрами и .
Решение (не открывайте сразу, сначала попробуйте решить самостоятельно)
Существует прямое и довольно утомительное решение с многочисленными матричными манипуляциями. Мы поступим хитрее: рассмотрим маргинализацию как линейное преобразование
и воспользуемся результатом предыдущего упражнения. Имеем , , и поэтому
.
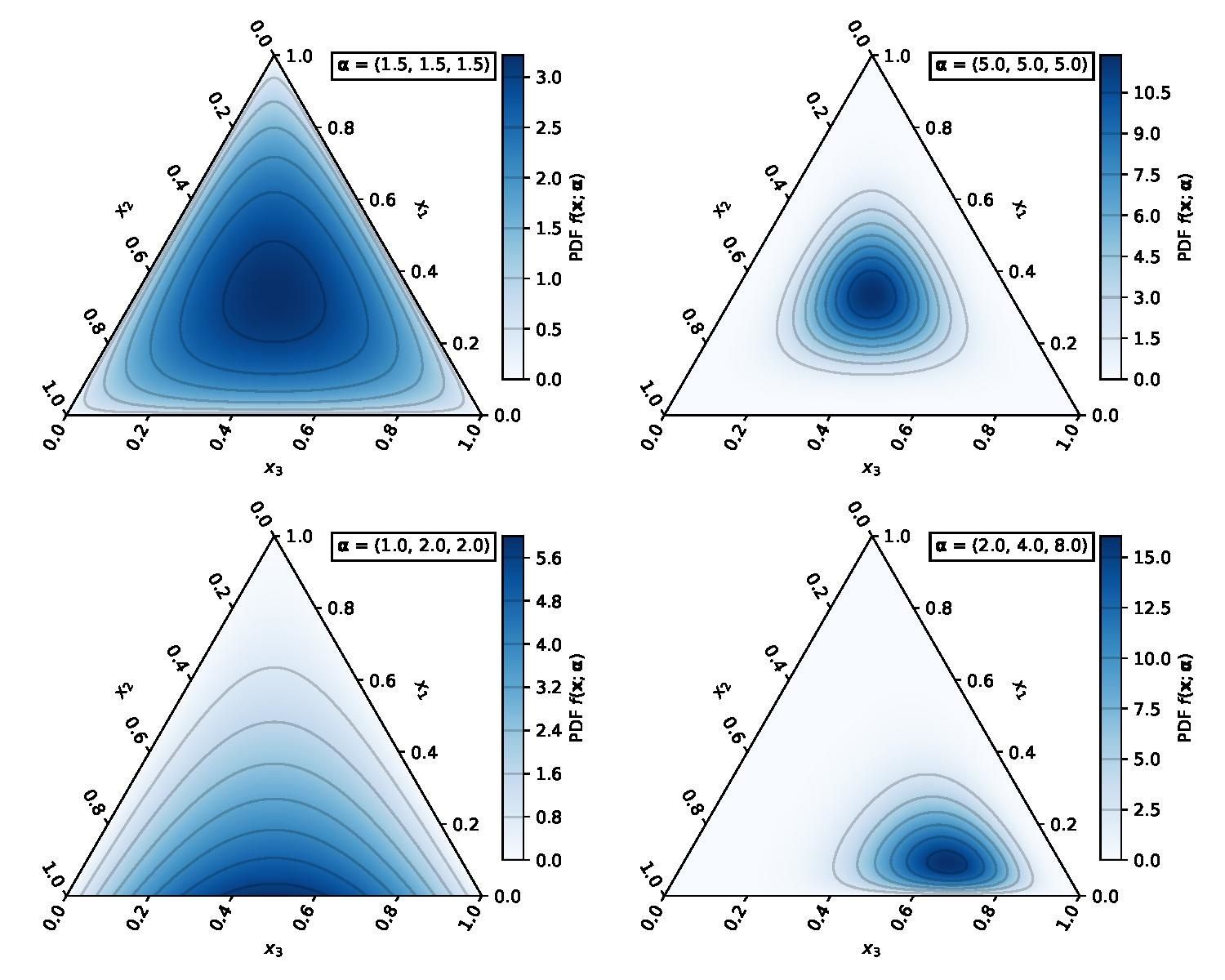
Распределение Дирихле
Распределение Дирихле сосредоточено на -мерном симплексе
Плотность распределения Дирихле равна
где – вектор положительных параметров, а – многомерная бета-функция. Если ,
то
Иллюстрация распределения Дирихле с помощью схемы Пойя
Пусть у нас есть категорий и на них задано вероятностное распределение
где . Это корректное распределение вероятностей, так как его компоненты неотрицательны и в сумме дают . Будем производить следующий процесс:
- В первый момент генерируем одну из категорий с помощью распределения ; допустим, выпала -я. Обновляем вероятностное распределение на категориях, прибавив единицу к -й компоненте вектора ; получаем вектор .
- На -м шаге генерируем одну из категорий с помощью распределения . Допустим, выпала -я. Обновляем вероятностное распределение на категориях, прибавив единицу к -й компоненте вектора ; получаем вектор .
Можно доказать, что вектор подчиняется распределению Дирихле .
Чтобы стало чуть понятнее, проследим, что будет при различных .
- Если , то прибавление единицы будет не так сильно смещать вероятности, и дальше мы будем продолжать генерировать категорию из распределения, близкого к равномерному. Скорее всего, в пределе мы будем получать что-то, близкое к .
- Если , то почти наверняка мы будем генерить третью категорию, причём со всё большей вероятностью (ведь при этом мы будем увеличивать ), то есть в пределе будет (почти , почти , почти ).
- Если , то та категория, которую мы сгенерировали на первом шаге, сразу вырвется вперёд и скорее всего будет доминировать в дальнейшем. Таким образом, нам следует ожидать в пределе векторов, в которых одна из компонент почти , а остальные почти . Важным отличием от предыдущего варианта является то, что здесь почти может быть в любой компоненте.
- Если , то соответствующее распределение Дирихле будет равномерным.
Также вам может оказаться полезна визуализация плотности этого распределения при разных :