В данном параграфе мы изучим инструмент, который позволяет анализировать ошибку алгоритма в зависимости от некоторого набора факторов, влияющих на итоговое качество его работы. Этот инструмент в литературе называется bias-variance decomposition — разложение ошибки на смещение и разброс. В разложении, на самом деле, есть и третья компонента — случайный шум в данных, но ему не посчастливилось оказаться в названии. Данное разложение оказывается полезным в некоторых теоретических исследованиях работы моделей машинного обучения, в частности, при анализе свойств ансамблевых моделей.
Некоторые картинки в тексте кликабельны. Это означает, что они были заимствованы из какого-то источника и при клике вы сможете перейти к этому источнику.
Вывод разложения bias-variance для MSE
Рассмотрим задачу регрессии с квадратичной функцией потерь. Представим также для простоты, что целевая переменная — одномерная и выражается через переменную как:
где — некоторая детерминированная функция, а — случайный шум со следующими свойствами:
В зависимости от природы данных, которые описывает эта зависимость, её представление в виде точной и случайной может быть продиктовано тем, что:
-
данные на самом деле имеют случайный характер;
-
измерительный прибор не может зафиксировать целевую переменную абсолютно точно;
-
имеющихся признаков недостаточно, чтобы исчерпывающим образом описать объект, пользователя или событие.
Функция потерь на одном объекте равна
Однако знание значения MSE только на одном объекте не может дать нам общего понимания того, насколько хорошо работает наш алгоритм. Какие факторы мы бы хотели учесть при оценке качества алгоритма? Например, то, что выход алгоритма на объекте зависит не только от самого этого объекта, но и от выборки , на которой алгоритм обучался:
Кроме того, значение на объекте зависит не только от , но и от реализации шума в этой точке:
Наконец, измерять качество мы бы хотели на тестовых объектах — тех, которые не встречались в обучающей выборке, а тестовых объектов у нас в большинстве случаев более одного. При включении всех вышеперечисленных источников случайности в рассмотрение логичной оценкой качества алгоритма кажется следующая величина:
Внутреннее матожидание позволяет оценить качество работы алгоритма в одной тестовой точке в зависимости от всевозможных реализаций и , а внешнее матожидание усредняет это качество по всем тестовым точкам.
Замечание. Запись в общем случае обозначает взятие матожидания по совместному распределению и . Однако, поскольку и независимы, она равносильна последовательному взятию матожиданий по каждой из переменных: , но последний вариант выглядит несколько более громоздко.
Попробуем представить выражение для в более удобном для анализа виде. Начнём с внутреннего матожидания:
Из общего выражения для выделилась шумовая компонента . Продолжим преобразования:
Таким образом, итоговое выражение для примет вид
где
— смещение предсказания алгоритма в точке , усреднённого по всем возможным обучающим выборкам, относительно истинной зависимости ;
— дисперсия (разброс) предсказаний алгоритма в зависимости от обучающей выборки ;
— неустранимый шум в данных.
Смещение показывает, насколько хорошо с помощью данного алгоритма можно приблизить истинную зависимость , а разброс характеризует чувствительность алгоритма к изменениям в обучающей выборке. Например, деревья маленькой глубины будут в большинстве случаев иметь высокое смещение и низкий разброс предсказаний, так как они не могут слишком хорошо запомнить обучающую выборку. А глубокие деревья, наоборот, могут безошибочно выучить обучающую выборку и потому будут иметь высокий разброс в зависимости от выборки, однако их предсказания в среднем будут точнее. На рисунке ниже приведены возможные случаи сочетания смещения и разброса для разных моделей:
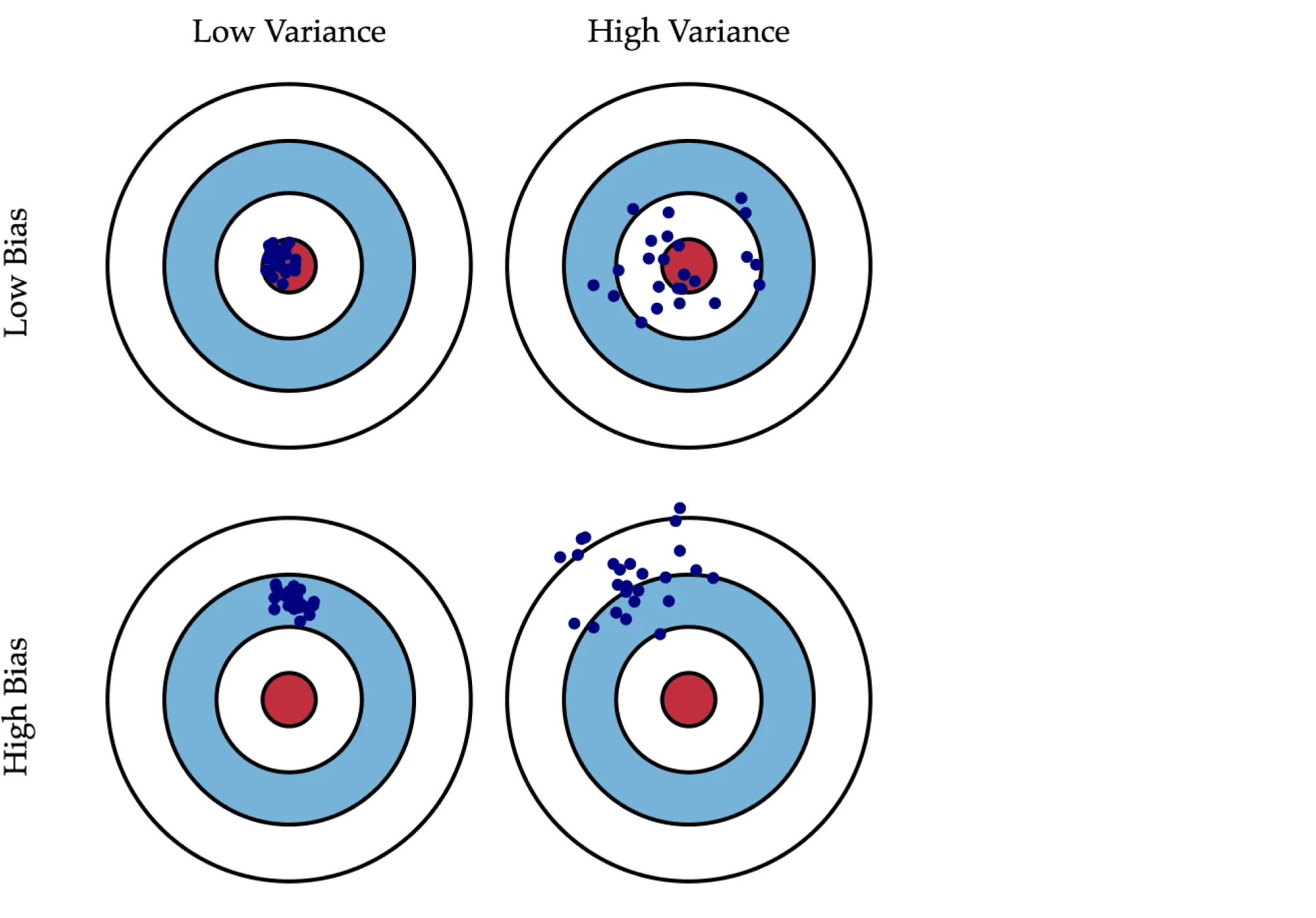
Синяя точка соответствует модели, обученной на некоторой обучающей выборке, а всего синих точек столько, сколько было обучающих выборок. Красный круг в центре области представляет ближайшую окрестность целевого значения. Большое смещение соответствует тому, что модели в среднем не попадают в цель, а при большом разбросе модели могут как делать точные предсказания, так и довольно сильно ошибаться.
Полученное нами разложение ошибки на три компоненты верно только для квадратичной функции потерь. Для других функций потерь существуют более общие формы этого разложения (Domigos, 2000, James, 2003) с похожими по смыслу компонентами. Это позволяет предполагать, что для большинства основных функций потерь имеется некоторое представление в виде смещения, разброса и шума (хоть и, возможно, не в столь простой аддитивной форме).
Пример расчёта оценок bias и variance
Попробуем вычислить разложение на смещение и разброс на каком-нибудь практическом примере. Наши обучающие и тестовые примеры будут состоять из зашумлённых значений целевой функции , где определяется как
В качестве шума добавляется нормальный шум с нулевым средним и дисперсией , равной во всех дальнейших примерах 9. Такое большое значение шума задано для того, чтобы задача была достаточно сложной для классификатора, который будет на этих данных учиться и тестироваться. Пример семпла из таких данных:
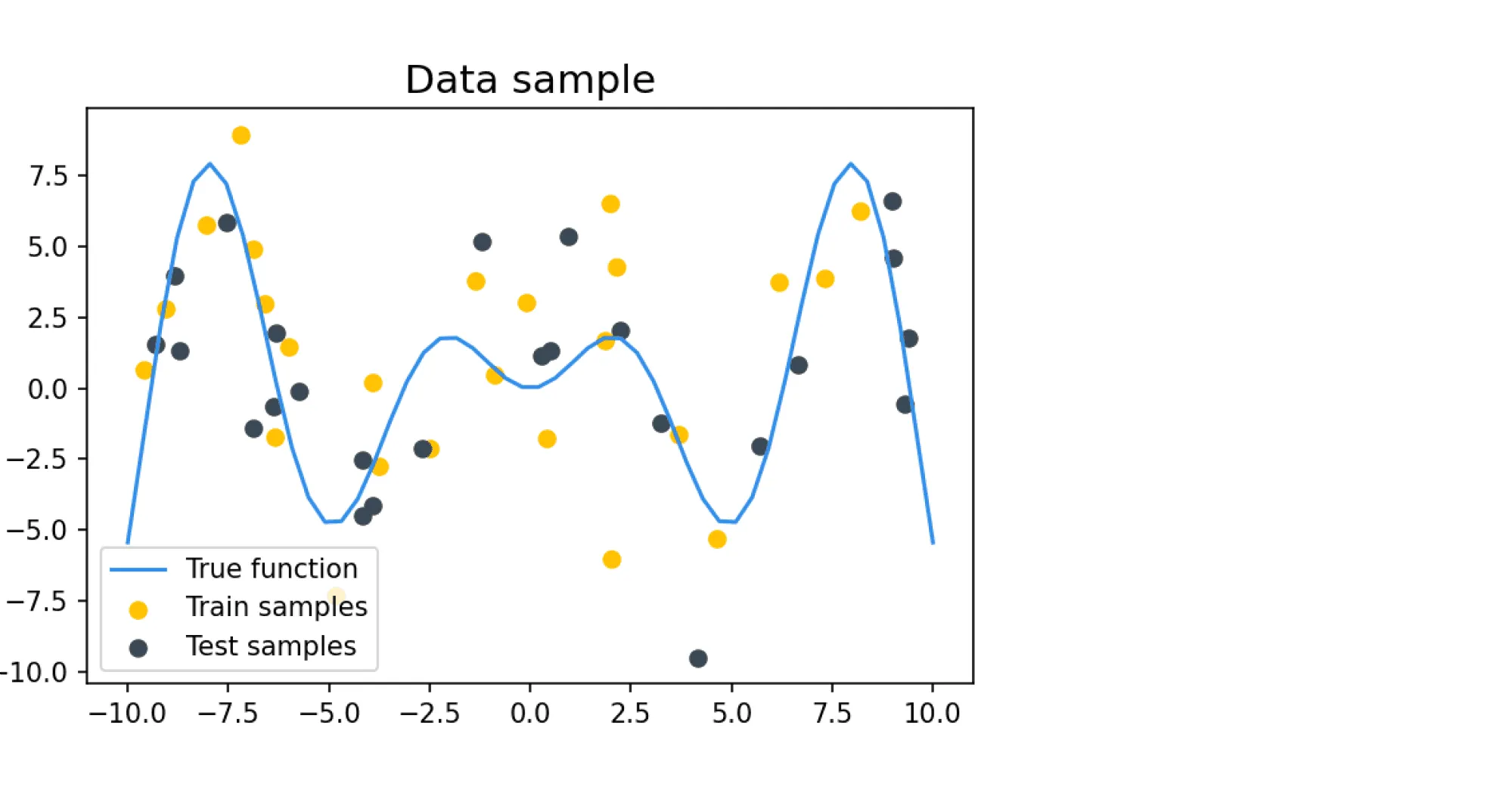
Посмотрим на то, как предсказания деревьев зависят от обучающих подмножеств и максимальной глубины дерева. На рисунке ниже изображены предсказания деревьев разной глубины, обученных на трёх независимых подвыборках размера 20 (каждая колонка соответствует одному подмножеству):
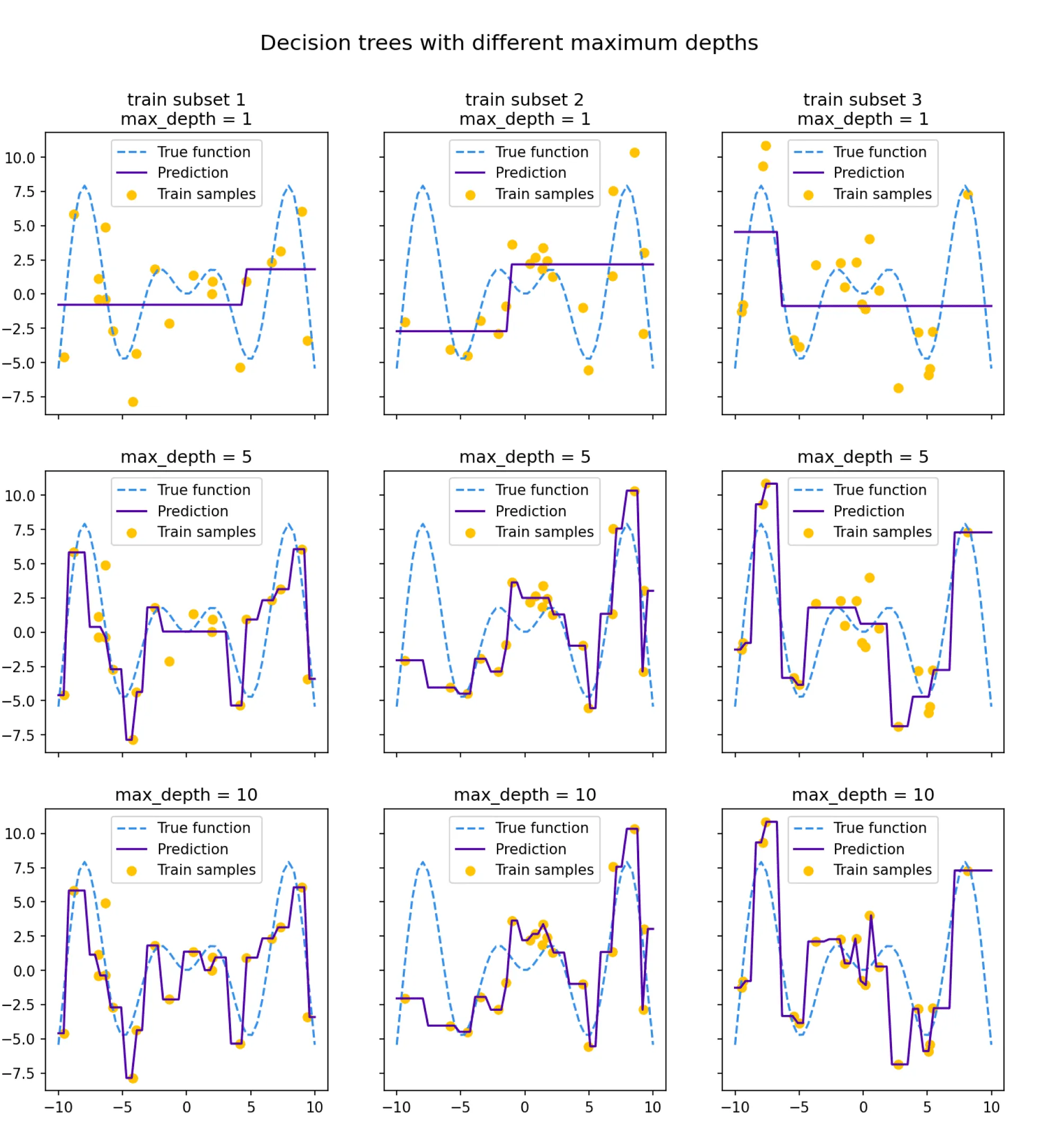
Глядя на эти рисунки, можно выдвинуть гипотезу о том, что с увеличением глубины дерева смещение алгоритма падает, а разброс в зависимости от выборки растёт. Проверим, так ли это, вычислив компоненты разложения для деревьев со значениями глубины от 1 до 15.
Для обучения деревьев насемплируем 1000 случайных подмножеств размера 500, а для тестирования зафиксируем случайное тестовое подмножество точек также размера 500. Чтобы вычислить матожидание по , нам нужно несколько экземпляров шума для тестовых лейблов:
Положим количество семплов случайного шума равным 300. Для фиксированных и квадратичная ошибка вычисляется как
Взяв среднее от по , и , мы получим оценку для , а оценки для компонент ошибки мы можем вычислить по ранее выведенным формулам.
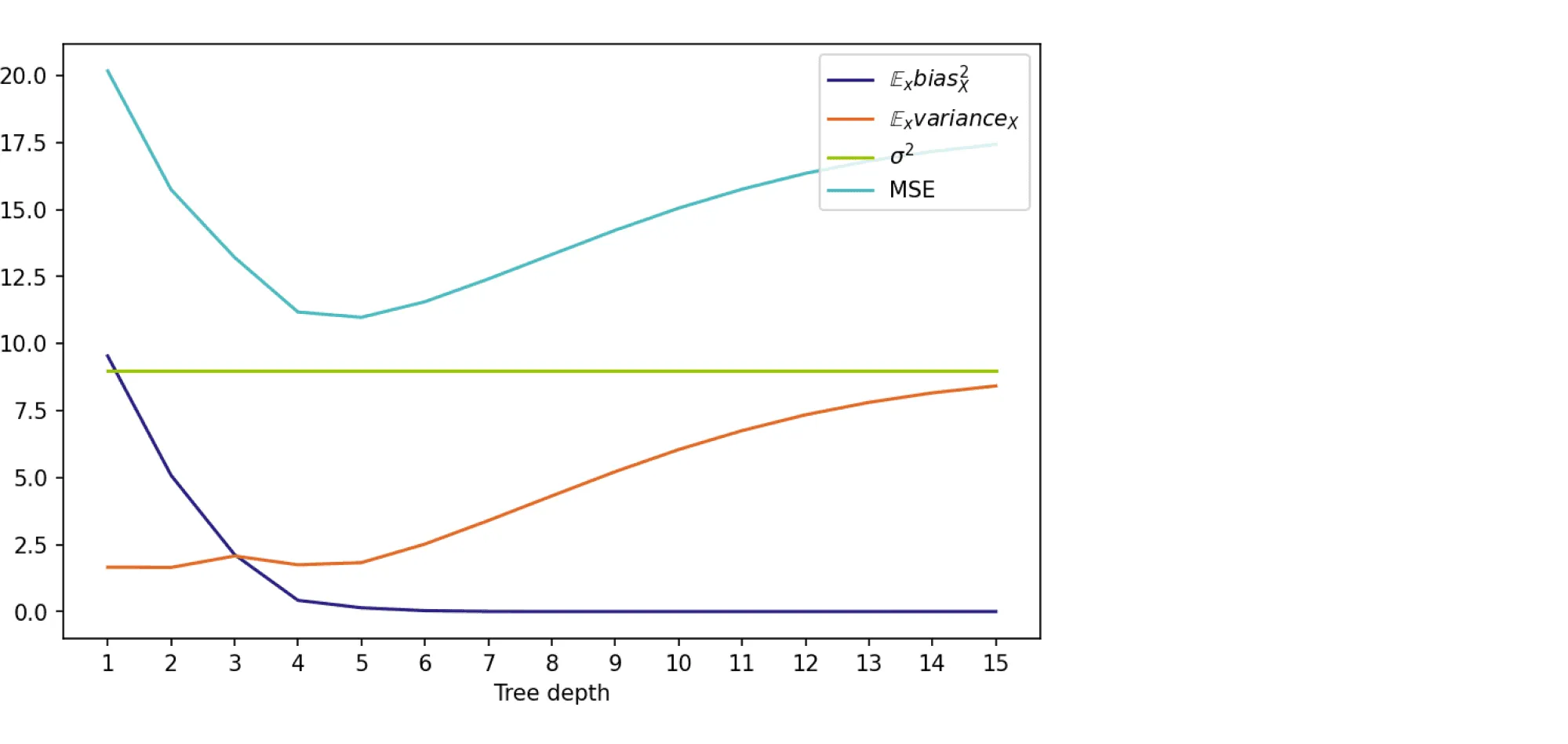
На графике ниже изображены компоненты ошибки и она сама в зависимости от глубины дерева:
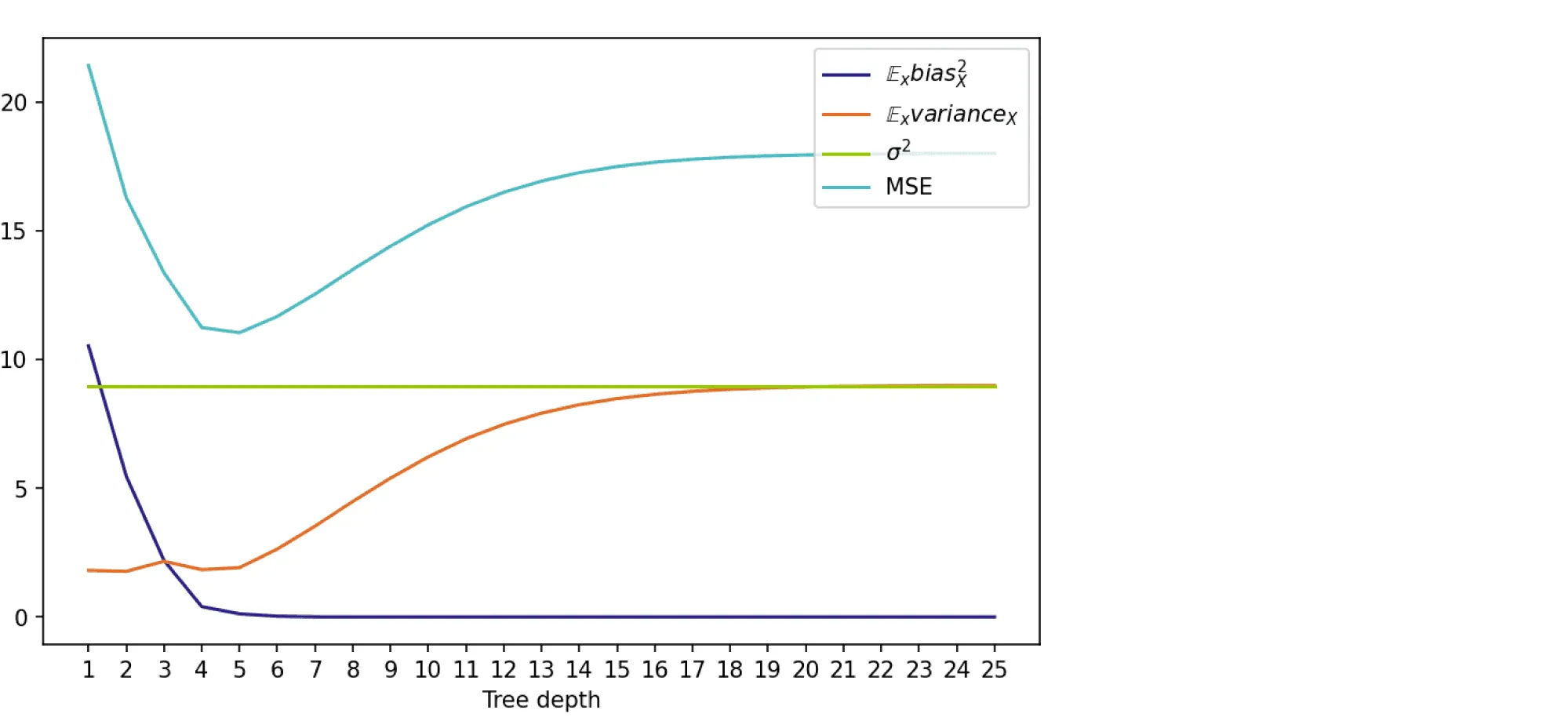
По графику видно, что гипотеза о падении смещения и росте разброса при увеличении глубины подтверждается для рассматриваемого отрезка возможных значений глубины дерева. Правда, если нарисовать график до глубины 25, можно увидеть, что разброс становится равен дисперсии случайного шума. То есть деревья слишком большой глубины начинают идеально подстраиваться под зашумлённую обучающую выборку и теряют способность к обобщению:
Код для подсчёта разложения на смещение и разброс, а также код отрисовки картинок можно найти в данном ноутбуке.
Bias-variance trade-off: в каких ситуациях он применим
В книжках и различных интернет-ресурсах часто можно увидеть следующую картинку:
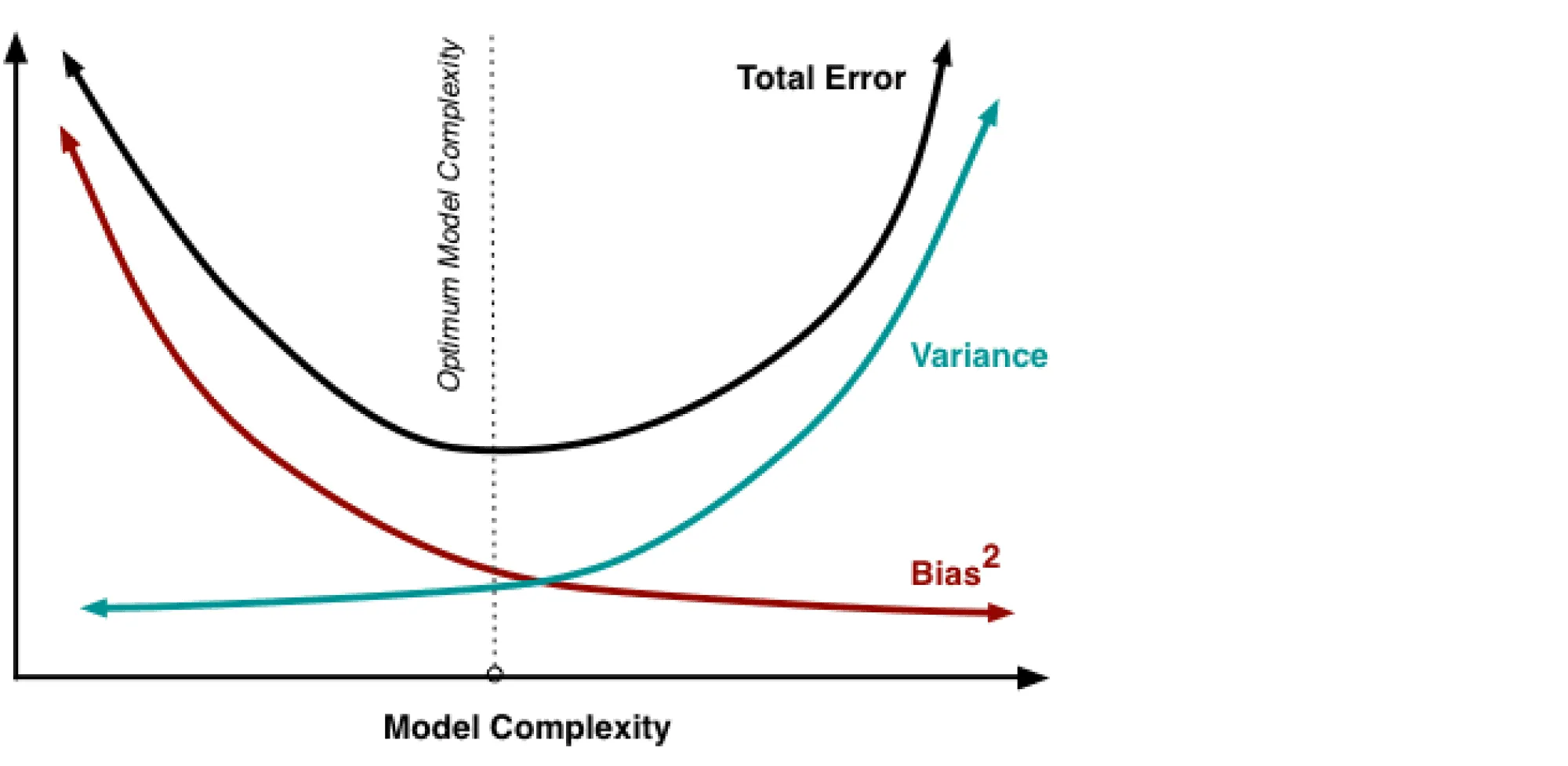
Она иллюстрирует утверждение, которое в литературе называется bias-variance trade-off: чем выше сложность обучаемой модели, тем меньше её смещение и тем больше разброс, и поэтому общая ошибка на тестовой выборке имеет вид -образной кривой. С падением смещения модель всё лучше запоминает обучающую выборку, поэтому слишком сложная модель будет иметь нулевую ошибку на тренировочных данных и большую ошибку на тесте. Этот график призван показать, что существует оптимальная сложность модели, при которой соблюдается баланс между переобучением и недообучением и ошибка при этом минимальна.
Существует достаточное количество подтверждений bias-variance trade-off для непараметрических моделей. Например, его можно наблюдать для метода ближайших соседей при росте и для ядерной регрессии при увеличении ширины окна (Geman et al., 1992):
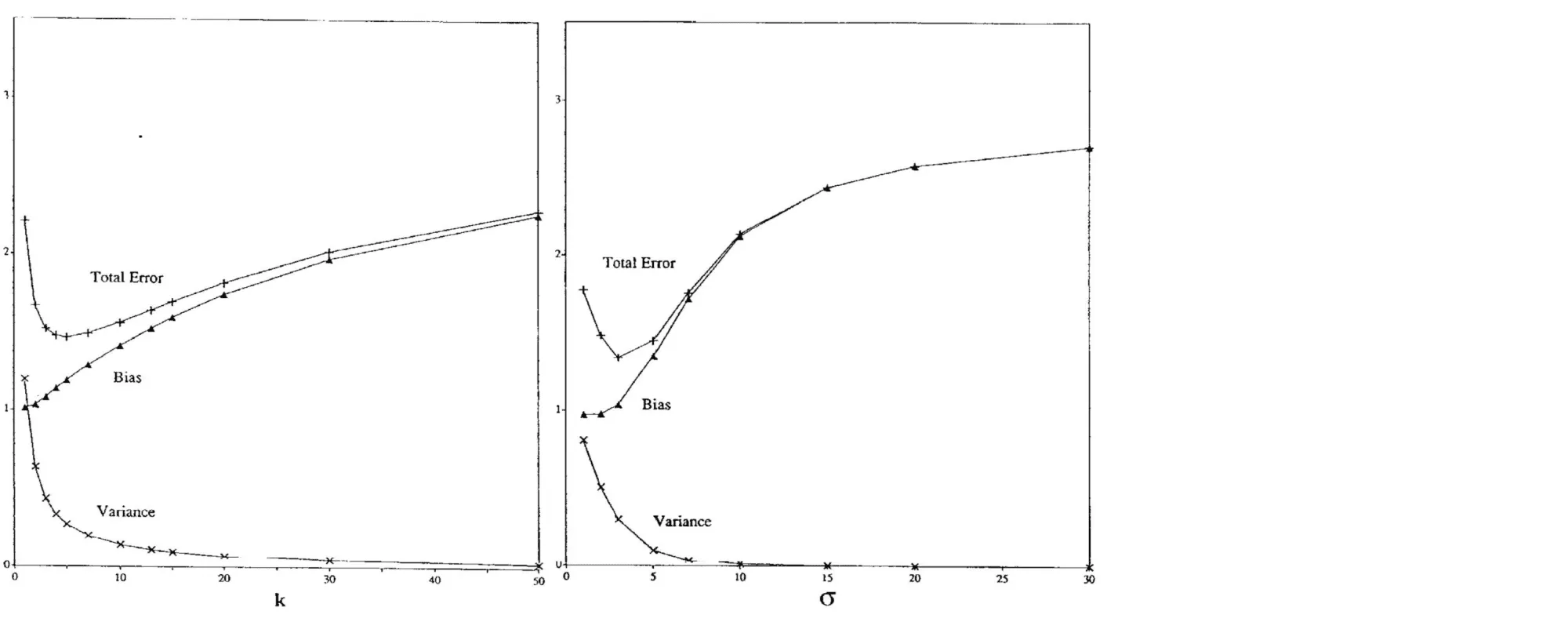
Чем больше соседей учитывает -NN, тем менее изменчивым становится его предсказание, и аналогично для ядерной регрессии, из-за чего сложность этих моделей в некотором смысле убывает с ростом и . Поэтому традиционный график bias-variance trade-off здесь симметрично отражён по оси .
Однако, как показывают последние исследования, непременное возрастание разброса при убывании смещения не является абсолютно истинным предположением. Например, для нейронных сетей с ростом их сложности может происходить снижение и разброса, и смещения. Одна из наиболее известных статей на эту тему — статья Белкина и др. (Belkin et al., 2019), в которой, в частности, была предложена следующая иллюстрация:
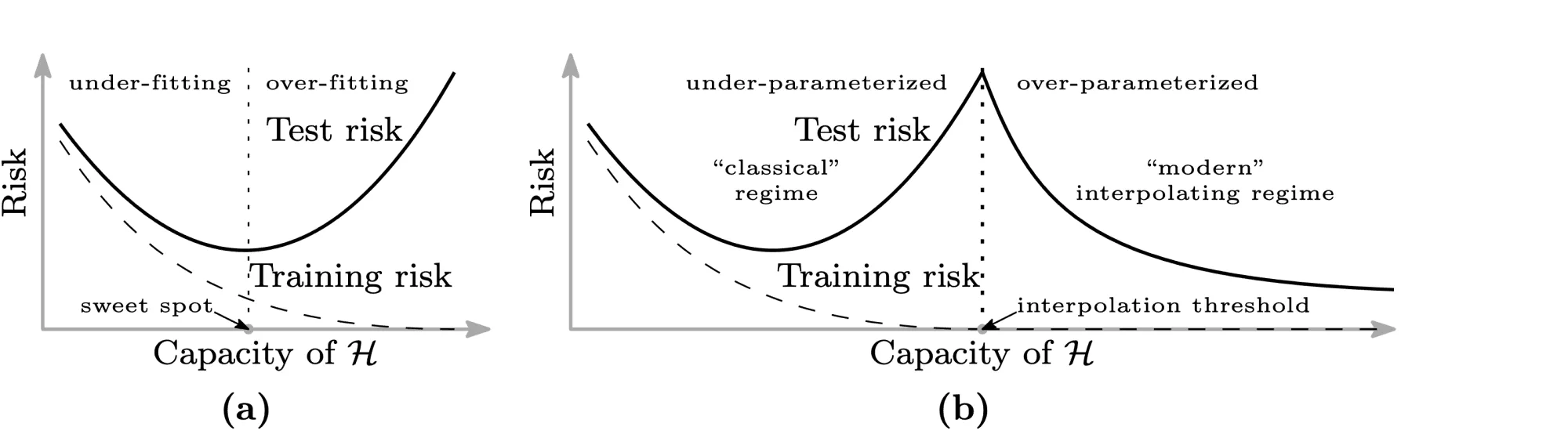
Слева — классический bias-variance trade-off: убывающая часть кривой соответствует недообученной модели, а возрастающая — переобученной. А на правой картинке — график, называемый в статье double descent risk curve. На нём изображена эмпирически наблюдаемая авторами зависимость тестовой ошибки нейросетей от мощности множества входящих в них параметров (). Этот график разделён на две части пунктирной линией, которую авторы называют interpolation threshold. Эта линия соответствует точке, в которой в нейросети стало достаточно параметров, чтобы без особых усилий почти идеально запомнить всю обучающую выборку. Часть до достижения interpolation threshold соответствует «классическому» режиму обучения моделей: когда у модели недостаточно параметров, чтобы сохранить обобщающую способность при почти полном запоминании обучающей выборки. А часть после достижения interpolation threshold соответствует «современным» возможностям обучения моделей с огромным числом параметров. На этой части графика ошибка монотонно убывает с ростом количества параметров у нейросети. Авторы также наблюдают похожее поведение и для «древесных» моделей: Random Forest и бустинга над решающими деревьями. Для них эффект проявляется при одновременном росте глубины и числа входящих в ансамбль деревьев.
В качестве вывода к этому разделу хочется сформулировать два основных тезиса:
- Bias-variance trade-off нельзя считать непреложной истиной, выполняющейся для всех моделей и обучающих данных.
- Разложение на смещение и разброс не влечёт немедленного выполнения bias-variance trade-off и остаётся верным и для случая, когда все компоненты ошибки (кроме неустранимого шума) убывают одновременно. Этот факт может оказаться незамеченным из-за того, что в учебных пособиях часто разговор о разложении дополняется иллюстрацией с -образной кривой, благодаря чему в сознании эти два факта могут слиться в один.
Список литературы
- Блог-пост про bias-variance от
Йоргоса Папахристудиса - Блог-пост про bias-variance от Скотта Фортмана-Роу
- Статьи от Домингоса (2000) и Джеймса (2003) про обобщённые формы bias-variance decomposition
- Блог-пост от Брейди Нила про необходимость пересмотра традиционного взгляда на bias-variance trade-off
- Статья Гемана и др. (1992), в которой была впервые предложена концепция bias-variance trade-off
- Статья Белкина и др. (2019), в которой был предложен double-descent curve



