Энтропия
Информативность наблюдений
Представим, что вы пронаблюдали значение некоторой случайной величины . Как измерить количество информации , которое вы при этом получили? Следующие соображения кажутся в этом плане вполне естественными:
- чем выше вероятность , тем более ожидаемо появление значения и, соответственно, менее информативно;
- и наоборот, наблюдение маловероятного значения обычно даёт обильную пищу для размышлений и повышает ;
- при наблюдении двух независимых реализаций и случайной величины логично складывать полученную информацию: .
Указанные соображения наводят на мысль, что информацию следует считать убывающей функцией от вероятности: . Кроме того, функция должна превращать произведение в сумму, поскольку для независимых случайных величин и
равенство влечёт
На самом деле выбор тут небогат. Единственная непрерывная функция, обладающая такими свойствами, — это логарифм: . Основание логарифма может быть любым числом больше единицы. Поскольку информацию измеряют в битах и байтах, в теории информации обычно предпочитают двоичные логарифмы. Однако для вычислений удобнее использовать натуральный логарифм, и по умолчанию мы будем подразумевать именно его (кстати, соответствующую единицу информации называют «нат»).
Энтропия Шеннона
Среднее количество информации, которое несёт в себе значение дискретной случайной с распределением вероятностей , вычисляется по формуле
Это так называемая энтропия (Шэннона).
Небольшое математическое замечание
При вычислении энтропии регулярно можно встретить выражение с не вполне очевидным значением. Поскольку , по определению полагаем
Пример. Рассмотрим схему Бернулли с вероятностью «успеха» . Энтропия её результата равна
Давайте посмотрим на график этой функции:

Минимальное значение (нулевое) энтропия принимает при или . Исход такого вырожденного эксперимента заранее известен, и чтобы сообщить кому-то о его результате, достаточно бит информации. Иначе говоря, можно вообще ничего не передавать, и так всё предельно ясно.
Максимальное значение энтропии достигается в точке , что вполне соответствует тому, что при предсказать исход эксперимента сложнее всего.
Упражнение. Найдите энтропию геометрического распределения с вероятностью «успеха» : ,
Решение (не открывайте сразу, попробуйте сначала решить самостоятельно)
По определению энтропии имеем
Дифференцированием геометрической прогрессии находим
подставляя сюда , окончательно получаем, что
Вспомним, что случайная величина равна количеству независимых испытаний с вероятностью «успеха» до появления первого «успеха». При энтропия минимальна и равна нулю, ведь в этом случае геометрическое распределение становится вырожденным: «успех» наступает сразу же с вероятностью . А вот при серия неудачных испытаний может быть сколь угодно длинной; распределение становится всё более неопределённым и «размазанным» по своему носителю, и его энтропия
стремится к . График энтропии как функции от выглядит так:

Следующие свойства энтропии дискретной случайной величины вытекают прямо из определения:
- неотрицательность: ;
- при некотором (нулевую энтропию имеют вырожденные распределения и только они);
- , если случайная величина имеет конечный носитель мощности .
Последнее свойство выводится из неравенства Йенсена. Применяя его к выпуклой вверх логарифмической функции, с учётом нормировки условия получаем
Вопрос на подумать. Итак, всякое распределение с носителем имеет энтропию не больше . А у какого распределения она в точности равна ?
Ответ (не открывайте сразу, сначала подумайте самостоятельно)
Такое произойдёт, если все вероятности , , т.е. распределение равномерное.
Дифференциальная энтропия
Чтобы вычислить энтропию непрерывной случайной величины , надо, как водится, сумму заменить на интеграл, и получится формула дифференциальной энтропии:
Замечание. В дальнейшем мы будем использовать одинаковый термин энтропия как для дискретных, так и для непрерывных случайных величин, для краткости опуская слово дифференциальная в последнем случае. Кроме того, энтропию распределения , заданного через pmf или pdf, будем обозначать . Такое обозначение позволяет избежать привязки к случайной величине там, где это излишне. Если , то обозначения и эквивалентны. Также отметим, что энтропию можно записать в виде математического ожидания:
Пример. Найдём энтропию нормального распределения . Его плотность равна , следовательно,
Делая в последнем интеграле замену , получаем, что
По свойству гамма-функции . Таким образом,
Как видно, энтропия гауссовского распределения не ограничена ни сверху, ни снизу:
И да, в отличие от энтропии дискретного распределения дифференциальная энтропия может быть отрицательной. Это связано с тем, что плотность может принимать значения больше единицы, и поэтому математическое ожидание её логарифма с обратным знаком может оказаться меньше нуля. В частности, с нормальным распределением так происходит, если .
Упражнение. Найдите энтропию показательного распределения .
Решение (не открывайте сразу, попробуйте сначала решить самостоятельно)
Плотность случайной величины равна , . Таким образом,
С помощью замены находим, что
KL-дивергенция
В задачах машинного обучения истинное распределение , из которого приходят наблюдения, обычно неизвестно, и его пытаются приблизить распределением из некоторого класса модельных распределений. Дивергенция Кульбака-Лейблера (KL-дивергенция, относительная энтропия) позволяет оценить расстояние между распределениями и :
в дискретном случае и
в непрерывном. KL-дивергенцию можно представить в виде разности:
Здесь вычитаемое – это уже знакомая нам энтропия распределения , которая показывает, сколько в среднем бит требуется, чтобы закодировать значение случайной величины . Уменьшаемое носит название кросс-энтропии распределений и .
Кросс-энтропию можно интерпретировать как среднее число бит для кодирования значения случайной величины алгоритмом, оптимизированным для кодирования случайной величины . Иными словами, дивергенция Кульбака-Лейблера говорит о том, насколько увеличится средняя длина кодов для значений , если при настройке алгоритма кодирования вместо использовать . Подробнее об этом вы можете почитать, например, в данном посте.
Дивергенция Кульбака-Лейблера в некотором роде играет роль расстояния между распределениями. В частности, , причём дивергенция равна нулю, только если распределения совпадают почти всюду (для дискретных и непрерывных распределений это означает, что они просто тождественны). Но при этом она не является симметричной: вообще говоря, .
Упражнение. Пользуясь неравенством , , докажите неотрицательность KL-дивергенции.
Попробуйте доказать самостоятельно, прежде чем смотреть решение
Указанное неравенство можно переписать в виде , , поэтому
Пример. С помощью KL-дивергенции измерим расстояние между двумя гауссианами и .
Подставляя явные выражения для плотностей
находим
Из свойств нормального распределения вытекает, что
Таким образом,
Как и должно быть, полученное выражение равно нулю, если гауссианы совпадают. При равных дисперсиях получаем, что . Это выражение остаётся прежним, если поменять местами и , поэтому в этом случае . Если же , то выражение для явно отличается от , что лишний раз показывает несимметричность KL-дивергенции.
Упражнение. Найдите дивергенцию Кульбака-Лейблера двух показательных распределений и .
Попробуйте решить самостоятельно, прежде чем смотреть решение
Имеем , , , откуда
Следовательно,
И здесь KL-дивергенция равна нулю при .
Кросс-энтропия
При определении KL-дивергенции мы уже встречались с кросс-энтропией
В зависимости от типа распределений кросс-энтропия вычисляется по формуле
Поскольку
задача минимизации KL-дивергенции между неизвестным распределением данных и модельным распределением эквивалентна задаче минимизации кросс-энтропии. Разница между ними равна энтропии распределения , которая, очевидно, не зависит от .
В машинном обучении кросс-энтропию часто используют в качестве функции потерь в задаче классификации на классов. Истинное распределение на каждом обучающем объекте задаётся с помощью one hot encoding и является вырожденным:
Классификатор обычно выдаёт вероятности принадлежности каждому из классов,
Функция потерь на одном объекте полагается равной кросс-энтропии между истинным и предсказанным распределениями:
И это вполне логично: чем ближе модельное распределение к истинному, тем меньше наши потери. В идеале , если .
Чтобы вычислить функцию потерь по обучающей выборке из объектов с метками , обычно берут усреднённную кросс-энтропию
Принцип максимальной энтропии
В параграфе про оценки параметров были описаны различные свойства параметрических оценок и методы их получения, например, метод моментов или метод максимального правдоподобия. В принципе, если мы уже выбрали для наших данных некоторое параметрическое семейство , моделирующее их распределение, восстановить его параметры чаще всего можно по выборочному среднему и/или выборочной дисперсии .
А теперь представим, что мы посчитали эти (или какие-то другие) статистики, а семейство распределений пока не выбрали. Как же совершить этот судьбоносный выбор? Давайте посмотрим на следующие три семейства и подумаем, в каком из них мы бы стали искать распределение, зная его истинные матожидание и дисперсию?
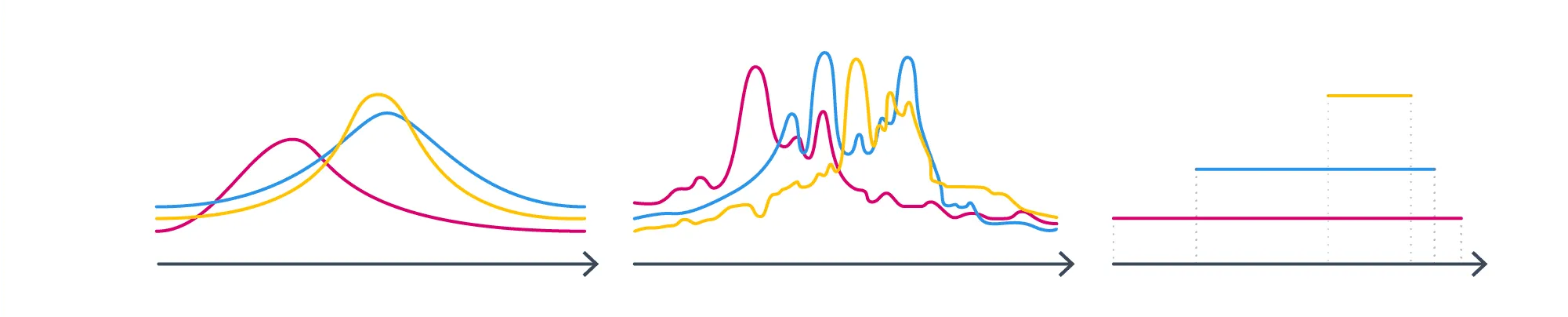
Почему-то хочется сказать, что в первом. Почему? Второе не симметрично – но что нас может заставить подозревать, что интересующее нас распределение не симметрично? С третьим проблема в том, что, выбирая его, мы добавляем дополнительную информацию как минимум о том, что у распределения конечный носитель. А с чего бы? У нас такой инфомации вроде бы нет.
Общая идея такова: мы будем искать распределение, которое удовлетворяет только явно заданным нами ограничениям и не отражает никакого дополнительного знания о нём. Таким образом, искомое распределение должно обладать максимальной неопределённостью при заданных ограничениях, или, говоря более научно, иметь максимально возможную энтропию. В самом деле, энтропия выражает нашу меру незнания о том, как ведёт себя распределение, и чем она больше – тем более «произвольное» распределение, по крайней мере, в теории. В этом и заключается принцип максимальной энтропии для выбора модели машинного обучения.
Как мы уже видели выше, среди распределений с конечным носителем максимальную энтропию имеет равномерное распределение. Примеры геометрического и нормального распределения показывают, что энтропия распределений с бесконечным носителем (счётным или континуальным) может быть сколь угодно большой, и среди них нет какого-то одного распределения с максимальной энтропией. Однако в более узком классе распределений с фиксированным средним и/или дисперсией найти распределение с максимальной энтропией, как правило, можно.
Пример. Покажем, что среди распределений на множестве натуральных чисел и математическим ожиданием максимальную энтропию имеет геометрическое распределение.
Для минимизации энтропии с учётом ограничений
воспользуемся методом множителей Лагранжа, согласно которому требуется минимизировать функцию Лагранжа
Приравняем к нулю частные производные по :
Отсюда следует, что , так что распределение действительно получается геометрическое. Параметры и найдём из уравнений
Деля первое уравнение на второе, получаем , или . Далее из первого уравнения находим . Итак,
а это и есть геометрическое распределение с параметром .
У непрерывных распределений возможны более интересные комбинации из ограничений на носитель и параметры. И конечно же, первую скрипку среди распределений с максимальной энтропией играет гауссовское распределение.
Пример. Докажем, что среди распределений на c математическим ожиданием и дисперсией наибольшую энтропию имеет нормальное распределение .
Пусть – некоторое распределение со средним и дисперсией , . Как было показано выше, . Запишем дивергенцию Кульбака-Лейблера:
Так как KL-дивергенция всегда неотрицательна, получаем, что при любом распределении , удовлетворяющем заданным ограничениям.
Можно показать, что максимальную энтропию среди многомерных распределений с вектором средних и матрицей ковариаций имеет также гауссовское распределение .
Упражнение. Докажите, что среди распределений на отрезке максимальную энтропию имеет равномерное распределение .
Попробуйте доказать самостоятельно, прежде чем смотреть решение.
Пусть , тогда для произвольного распределения на отрезке имеем
В частности, отсюда следует, что . Расписывая теперь KL-дивергенцию, получаем
что и требовалось доказать.
Упражнение. Докажите, что среди распределений на промежутке с математическим ожиданием максимальную энтропию имеет показательное распределение .
Попробуйте доказать самостоятельно, прежде чем смотреть решение.
Согласно результату одного из предыдущих упражнений , если , т.е. , . Далее, для произвольного распределения на со средним имеем
Как выяснилось, многие классические распределения имеют максимальную энтропию при весьма естественных ограничениях. Но как быть, если даны не эти конкретные, а какие-то другие ограничения? Есть ли какой-нибудь надёжный алгоритм вывода распределения с максимальной энтропией, позволяющий избежать случайных озарений и гаданий на кофейной гуще? Оказывается, что при некоторых не очень обременительных ограничениях ответ можно записать с помощью распределений экспоненциального класса.
Экспоненциальное семейство распределений
Говорят, что параметрическое семейство распределений относится к экспоненциальному классу, если его pdf (или pmf) может быть представлена в виде
где
- – вектор натуральных параметров распределения;
- — неотрицательная функция (base measure), часто равная единице;
- — нормализатор (partition), обеспечивающий суммируемость pmf или интегрируемость pdf в единицу:
- — log-partition;
- — вектор достаточных статистик распределения.
Пример. Покажем, что нормальное распределение принадлежит экспоненциальному классу. Оно имеет два параметра, поэтому такую же размерность имеют и вектор-функция .
Распишем плотность:
Положим , ,
Остаётся выразить функцию через и .
Упражнение. Выразите partition и log-partition через и запишите плотность нормального распределения в экспоненциальном виде.
Ответ
Пример. Покажем, что распределение Бернулли принадлежит экспоненциальному классу. Его pmf можно записать как
Параметр здесь один, поэтому натуральный параметр тоже один: . Такая функция от называется функцией логитов и активно участвует в построении модели логистической регрессии. Остальные функции положим равными , , . Остаётся выразить partition через :
Итак, , и экспоненциальный вид распределения Бернулли записывается как
Вопрос на подумать. Принадлежит ли к экспоненциальному классу семейство равномерных распределений на отрезках ? Казалось бы, да, ведь
В чём может быть подвох?
Попробуйте определить сами, прежде чем смотреть ответ.
Нет, не принадлежит. Давайте вспомним, как звучало определение экспоненциального семейства. Возможно, вас удивило, что там было написано не «распределение относится», а «семейство распределений относится». Это важно: ведь семейство определяется именно различными значениями , и если нас интересует семейство равномерных распределений на отрезках, определяемое параметрами и , то они не могут быть в функции , они должны быть под экспонентой, а экспонента ни от чего не может быть равна индикатору.
При этом странное и не очень полезное семейство с нулём параметров, состоящее из одинокого распределения можно считать относящимся к экспоненциальному классу: ведь для него формула
будет работать.
К экспоненциальным семействам относятся многие непрерывные и дискретные распределения из часто встречающихся в теории и на практике, в том числе
- нормальное ;
- распределение Пуассона ;
- экспоненциальное ;
- биномиальное ;
- геометрическое ;
- бета-распределение;
- гамма-распределение;
- распределение Дирихле.
Как выглядят натуральные параметры, достаточные статистики и нормализаторы этих и других распределений из экспоненциального класса, можно посмотреть на википедии.
К экспоненциальным семействам не относятся, например, равномерное распределение , -распределение Стьюдента, распределение Коши, смесь нормальных распределений.
Дифференцирование log-partition
Если распределение принадлежит экспоненциальному классу,
то моменты его достаточных статистик могут быть получены дифференцированием функции .
Утверждение. .
Доказательство.
По правилу дифференцирования сложной функции имеем
Нормализатор записывается в виде интеграла
который мы продифференцируем внесением градиента внутрь под знак интеграла:
Таким образом,
Замечание о дифференцировании под знаком интегралом
Использованный в доказательстве приём внесения градиента под знак интеграла называют также правилом Лейбница. Этот же метод используется для почленного дифференцирования ряда, что может быть полезно в случае дискретного распределения . В математическом анализе имеется ряд теорем, обеспечивающих применимость правила Лейбница, однако, мы не будем на них останавливаться. Будем считать, что все рассматриваемые экспоненциальные семейства таковы, что применение правила Лейбница законно.
Если , то в соответствии с только что доказанным частная производная даёт -й момент распределения .
Упражнение. Вычислите производные по натуральным параметрам от log-partition для распределения Бернулли и нормального распределения и проверьте, что они совпадают со значениями соответствующих моментов.
Решение
Для имеем
поэтому
Для гауссовской случайной величины получаем
и, значит,
Кстати, можно продифференцировать ещё раз и доказать, что
Доказательство
В предыдущий раз мы доказали, что
Теперь возьмём ещё раз градиент по от этого выражения:
В последней выкладке для краткости обозначено .
MLE для семейства из экспоненциального класса
Возможно, вас удивил странный и на первый взгляд не очень естественный вид . Но всё не просто так: оказывается, что оценка максимального правдоподобия параметров распределений из экспоненциального класса устроена очень интригующе.
Запишем функцию правдоподобия i.i.d. выборки :
Её логарифм равен
Дифференцируя по , получаем
Приравнивая к нулю и пользуясь равенством , находим
Таким образом, теоретические матожидания всех компонент должны совпадать с их эмпирическими оценками, а метод максимального правдоподобия совпадает с методом моментов для в качестве моментов. И в следующем пункте выяснится, что распределения из экспоненциальных семейств обладают максимальной энтропией среди тех, что имеют заданные моменты .
Теорема Купмана—Питмана—Дармуа
Теперь мы наконец готовы сформулировать одно из самых любопытных свойств семейств экспоненциального класса.
В следующей теореме мы опустим некоторые не очень обременительные условия регулярности. Просто считайте, что для хороших дискретных и абсолютно непрерывных распределений, с которыми вы в основном и будете сталкиваться, это так.
Теорема. Пусть параметр распределения выбран так, что
для некоторого фиксированного . Тогда распределение обладает наибольшей энтропией среди распределений с тем же носителем, для которых .
Идея обоснования через оптимизацию.
Мы приведём рассуждение для дискретного случая; в абсолютно непрерывном рассуждения будут по сути теми же, только там придётся дифференцировать не по переменных, а по функциям, и мы решили не ввергать читателя в мир вариационного исчисления.
В дискретном случае у нас есть счётное семейство точек , и распределение определяется счётным набором вероятностей принимать значение . Мы будем решать задачу
Для решения этой оптимизационной задачи нам понадобится обобщение метода множителей Лагранжа, известное также как теорема Каруша—Куна—Таккера. В данном случае задача сводится к минимизации лагранжиана
при имеющихся ограничениях и условиях дополняющей нежёсткости .
Приравняем частные производные по к нулю:
Отсюда получаем, что
Числитель уже ровно такой, как и должен быть у распределения из экспоненциального класса; разберёмся со знаменателем. Поскольку (ведь тут сплошные экспоненты), при всех . Параметр находится из условия , а точнее, выражается через остальные , что позволяет записать знаменатель в виде .
Идея доказательства «в лоб».
Как и следовало ожидать, оно ничем не отличается от того, как мы доказывали максимальность энтропии у равномерного или нормального распределения. Пусть – ещё одно распределение, для которого
для всех . Тогда
Таким образом, , что и требовалось доказать.
Выше мы уже находили обладающее максимальной энтропией распределение на множестве натуральных чисел с заданным математическим ожиданием . Таковым оказалось геометрическое распределение .
Теорема Купмана—Питмана—Дармуа позволяет сделать это гораздо быстрее.
В данном случае у нас лишь одна функция , которая соответствует фиксации математического ожидания . Искомое дискретное распределение имеет вид
Это уже похоже на геометрическое распределение с параметром . Его математическое ожидание равно , что по условию должно равняться . Итак, наше распределение с максимальной этропией выглядит так:
Пример. Среди распределений на всей вещественной прямой с заданным математическим ожиданием найдём распределение с максимальной энтропией.
А сможете ли вы его найти? Решение под катом.
Теория говорит нам, что его плотность должна иметь вид
но интеграла экспоненты не существует, то есть применение «в лоб» теоремы провалилось. И неспроста: если даже рассмотреть все нормально распределённые случайные величины со средним , их энтропии, равные , не ограничены сверху, то есть величины с наибольшей энтропией не существует.


