2.2. Метрические методы

Смысл метрических методов очень хорошо раскрывает фраза «Скажи мне, кто твой друг, и я скажу, кто ты». Алгоритмы этого класса почти не имеют фазы обучения. Вместо этого они просто запоминают всю обучающую выборку, а на этапе предсказания просто ищут объекты, похожие на целевой.

Такой процесс называют lazy learning, потому что никакого обучения, по сути, не происходит. Также метрические модели являются непараметрическими, потому что они не делают явных допущений о глобальных законах, которым подчиняются данные. Так, линейная регрессия основывается на предположении о том, что изучаемая закономерность линейная (с неизвестными коэффициентами, которые восстанавливаются по выборке), а линейная бинарная классификация — что существует гиперплоскость, неплохо разделяющая классы. Метрические методы же локальны: они исходят из допущения, что свойства объекта можно узнать, имея представление о его соседях.

Указанные выше свойства могут быть полезными, особенно в случае сложно устроенных данных, для которых мы не можем придумать глобальную модель. Однако с другой стороны, из-за lazy learning алгоритм становится абсолютно неприменимым при большом количестве данных. Несмотря на то, что эти алгоритмы очень просты для понимания, они довольно точны и хорошо интерпретируемы — и часто используются как минимум в качестве бейзлайнов в разных задачах.

В первой части параграфа мы расскажем об одном из самых известных метрических алгоритмов — методе k-ближайших соседей (k-nearest neighbors, KNN). Этот подход в основном чисто инженерный из-за отсутствия фазы обучения — в настоящее время уже почти нигде не применяется. Однако многие техники, на которых основан алгоритм, используются и в других методах.

Например, у алгоритмов поиска ближайших соседей, — неотъемлемой часть метода, — намного более широкая область применения. Плюс ко всему KNN — очень простой и легко интерпретируемый алгоритм, поэтому изучить его всё равно полезно. Мы обсудим подробнее его преимущества, недостатки, область его применения, а также возможные обобщения.

Для метрических методов очень важно уметь эффективно находить ближайшие объекты, поэтому задача их поиска неизбежно возникает при применении любого такого алгоритма. Поэтому во второй части параграфа мы рассмотрим возможные подходы к быстрому поиску ближайших соседей.

Метод k-ближайших соседей (KNN)

Представим, что мы проводим классификацию объектов на два класса — красный или жёлтый. Нам дана некоторая обучающая выборка и целевой объект (серый):

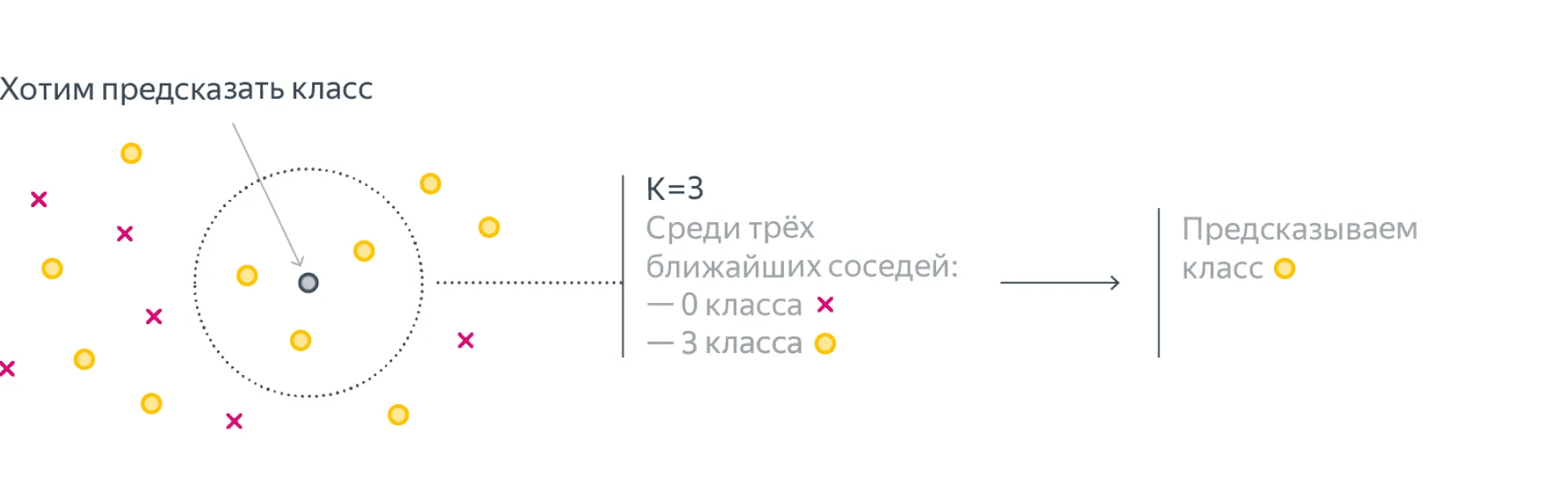
Мы хотим определить, к какому классу относится серый объект. Интуитивно очевидно, что он должен быть жёлтым, потому что все его соседи жёлтые. Эта интуиция и отражает суть метода KNN — классифицировать целевой объект, исходя из того, какие классы у объектов, которые максимально похожи на него.

Перейдём теперь к более формальному описанию алгоритма. Рассмотрим сначала задачу многоклассовой классификации, а регрессией займёмся позже.

Пусть дана обучающая выборка , где . Пусть также задана некоторая симметричная по своим аргументам функция расстояния . Предположим, что требуется классифицировать новый объект . Для этого найдём наиболее близких к в смысле расстояния объектов обучающей выборки :

Метку класса объекта будем обозначать . Класс нового объекта тогда естественным образом определим как наиболее часто встречающийся класс среди объектов из :

Формула может показаться страшной, но на самом деле всё довольно просто: для каждой метки класса количество соседей с такой меткой можно посчитать, просто просуммировав по всем соседям индикаторы событий, соответствующих тому, что метка соседа равна .

Легко заметить, что этот алгоритм позволяет также оценивать вероятности классов. Для этого достаточно просто посчитать частоты классов соседей:

Стоит, однако, понимать, что, хоть такая функция и удовлетворяет свойствам вероятности (она неотрицательна, аддитивна и ограничена единицей), это не более чем эвристика.

Несмотря на то что формально фаза обучения отсутствует, алгоритм может легко переобучиться. Вы можете убедиться в этом сами, использовав маленькое количество соседей (например, одного или двух), — границы классов оказываются довольно сложными. Происходит это из-за того, что параметрами алгоритма можно считать всю обучающую выборку, довольно большую по размеру. Из-за этого алгоритму легко подстроиться под конкретные данные.

По ссылке вы можете увидеть интерактивный пример работы алгоритма. Автор примера - Анастасия Чирикова.

Выбор метрики

Может возникнуть закономерный вопрос, как же правильно выбрать функцию расстояния . В подавляющем большинстве случаев обычное евклидово расстояние будет хорошим выбором. Однако в некоторых случаях другие функции будут подходить лучше, поэтому давайте разберём ещё несколько функций, наиболее используемых на практике.

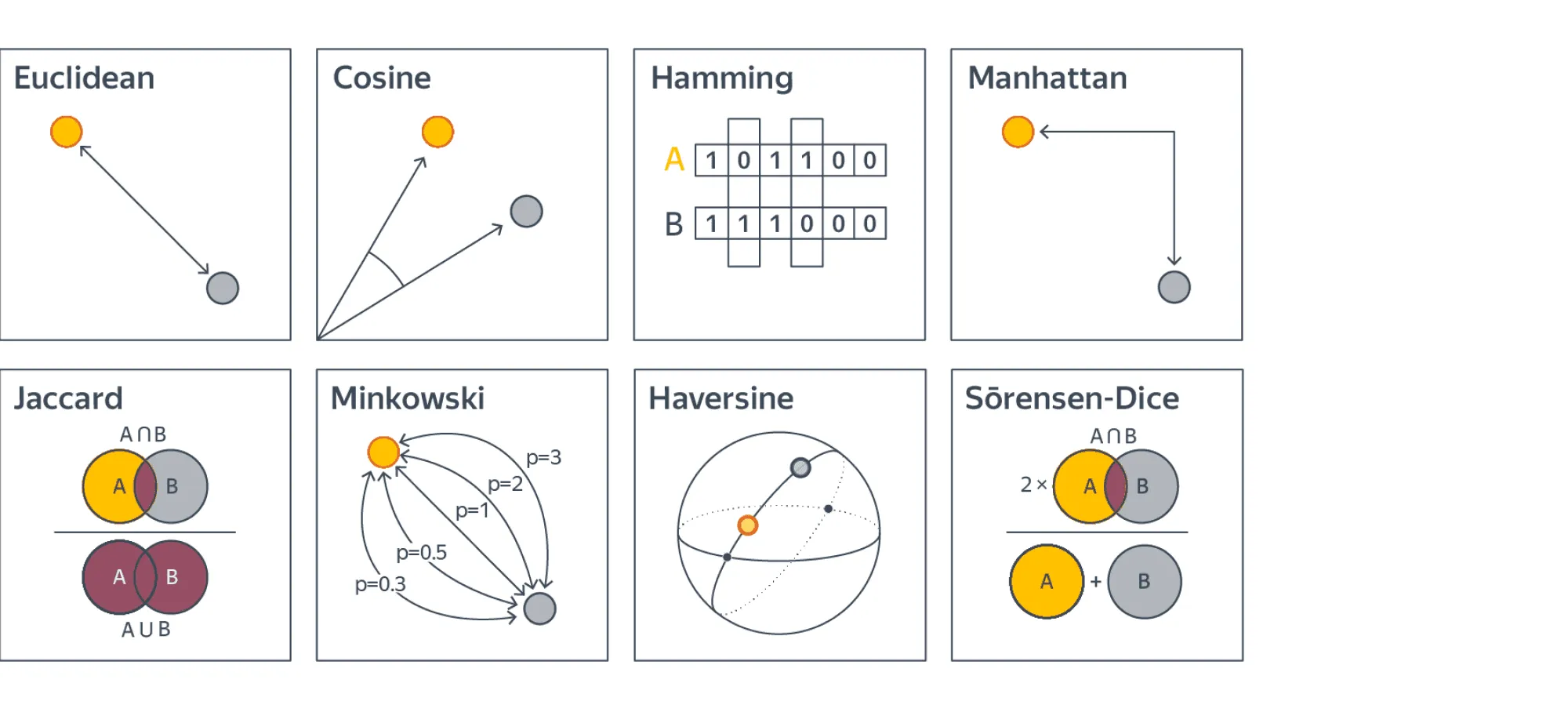
Манхэттенская метрика

Часто используется в высокоразмерных пространствах из-за лучшей устойчивости к выбросам. Представим, что два объекта в 1000-размерном пространстве почти идентичны, но сильно отличаются по одному из признаков. Это почти наверняка свидетельствует о выбросе в этом признаке, и объекты, скорее всего, очень близки. Однако евклидово расстояние усилит различие в единственном признаке и сделает их более далёкими друг от друга. Этого недостатка лишена манхэттенская метрика — в ней вместо квадрата используется модуль.

Метрика Минковского

Является обобщением евклидовой () и манхэттенской () метрик.

Косинусное расстояние

Эта метрика хороша тем, что не зависит от норм векторов. Такое поведение бывает полезно в некоторых задачах, например при поиске похожих документов. В качестве признаков там часто используются количества слов. При этом интуитивно кажется, что если в тексте использовать каждое слово в два раза больше, то тема этого текста поменяться не должна. Поэтому как раз в этом случае нам не важна норма вектор-признака, и в задачах, связанных с текстами, часто применяется именно косинусное расстояние.

Расстояние Жаккара

Его стоит использовать, если исследуемые объекты — это некоторые множества. Это полезно тем, что нет нужды придумывать векторные представления для этих множеств, чтобы использовать традиционные метрики.

Вообще говоря, несмотря на некоторые эвристические соображения по выбору метрики, её можно считать гиперпараметром и подбирать соответствующими способами. Часто качество модели сильно зависит от выбора метрики, а иногда выбрать правильную метрику очень тяжело. Например, в случае когда данные имеют сильно разный масштаб, выбрать подходящую метрику почти невозможно, и нужно сперва проводить нормализацию.

Замечание. Упомянутые в этом параграфе функции мы называем «метриками», но, конечно же, они не обязаны быть метриками в строгом математическом смысле. Они неотрицательны и симметричны, но могут не удовлетворять неравенству треугольника.

Обобщения алгоритма

Взвешенный KNN

У оригинального алгоритма есть один большой недостаток: он никак не учитывает расстояния до соседних объектов, хотя эта информация может быть полезной.

Давайте попробуем придумать, как исправить этот недостаток. Нам нужно каким-то образом увеличивать вклад близких объектов и уменьшать вклад далёких. Можно заметить, что все индикаторы в формуле учитываются в сумме с одинаковыми коэффициентами. Возникает идея — назначить этим индикаторам веса, которые тем больше, чем ближе объект к целевому. Таким образом, получаем следующую формулу:

Такой алгоритм называется взвешенным KNN (weighted KNN).

Есть множество вариантов выбора весов для объектов, которые можно поделить на две большие группы. В первой группе веса зависят лишь от порядкового номера объекта в отсортированном по близости к массиве . Чаще всего затухающие веса берутся линейно или экспоненциально .

Однако здесь мы также не используем всю информацию, которая нам доступна. Зачем использовать порядок соседей, порождаемый расстояниями, если можно использовать сами расстояния?

Во второй группе методов вес — это некоторая функция от расстояния. Давайте подумаем, какие должны быть свойства у этой функции.

• Очевидно, она должна быть положительной на своей области определения, иначе модель будет поощрять несовпадение с некоторыми ближайшими соседями.
• Также необходимо, чтобы функция монотонно не возрастала, чтобы вес близких соседей был больше, чем далёких.

Таким образом вводится так называемая ядерная функция (kernel function) , обладающая перечисленными выше свойствами, с помощью которой и высчитывается вес каждого соседа:

где — некое положительное число, которое называется шириной окна.

От выбора ядра зависит гладкость аппроксимации, но на её качество этот выбор почти не влияет. Примеры ядерных функций в порядке увеличения их гладкости:

• — прямоугольное ядро;
• — треугольное ядро (непрерывное);
• — ядро Епанечникова (гладкое везде, кроме –1 и 1);
• — биквадратное ядро (гладкое везде);
• — гауссовское ядро (бесконечно гладкое везде).

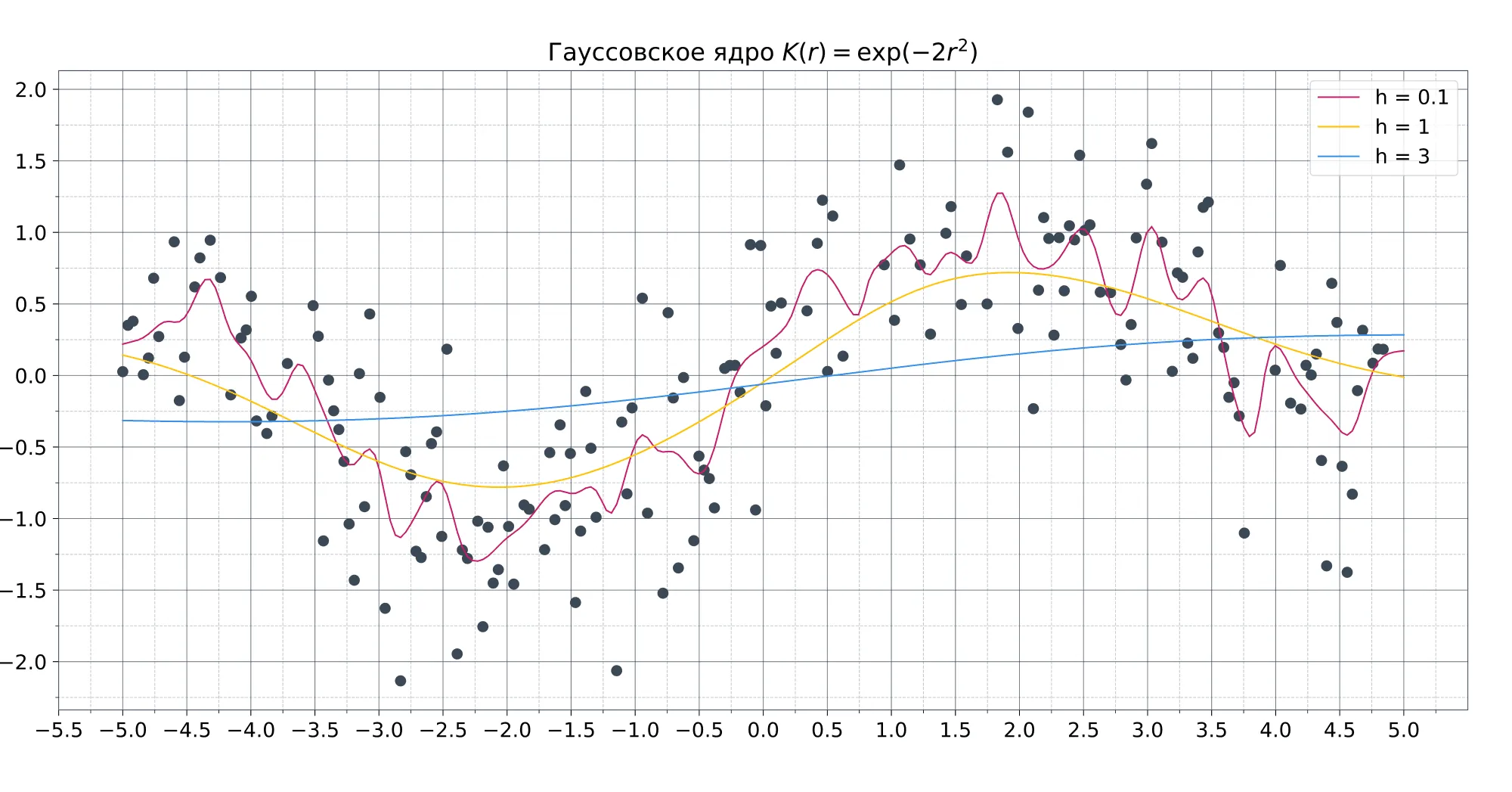
На практике чаще всего используют либо прямоугольное для простоты, либо гауссовское, в случае когда важна гладкость модели (немного забегая вперёд — это особенно важно в регрессии).

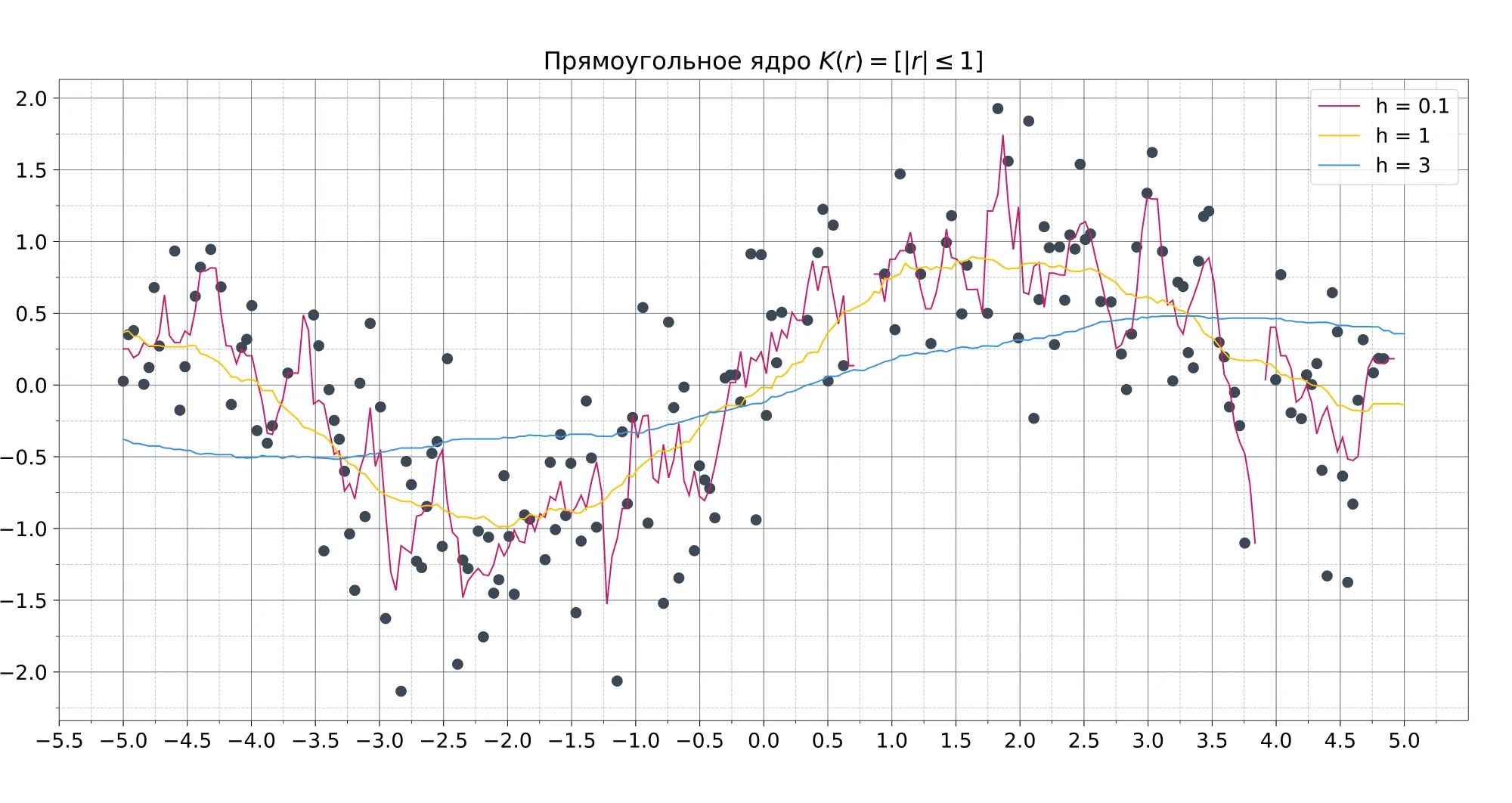
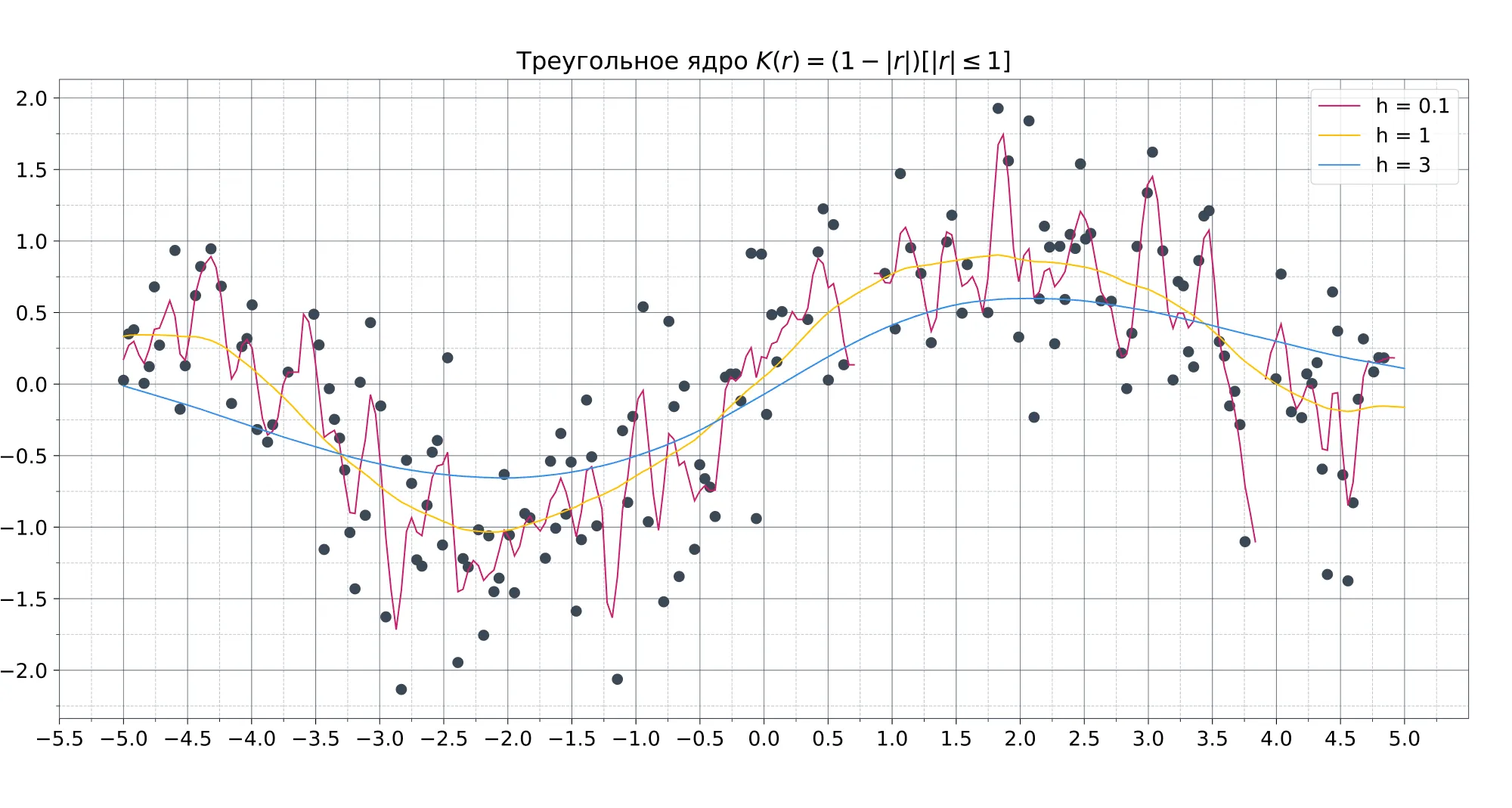
Ширина окна, в свою очередь, сильно влияет как раз на качество модели. При слишком маленькой ширине модель сильно подстраивается под обучающую выборку и теряет свою обобщающую способность. При слишком большой ширине, напротив, модель становится слишком простой. Универсальной ширины окна не существует, поэтому для каждой задачи её приходится подбирать отдельно.

Kernel regression

Алгоритм KNN можно довольно легко обобщить и на задачу регрессии. Самые очевидные способы — брать для некоторого ядра либо обычное среднее:

либо взвешенный вариант:

Последняя формула называется формулой Надарая — Ватсона. Она — один из непараметрических методов восстановления регрессии, объединённых названием ядерная регрессия (kernel regression).

Выписать ответ, конечно, просто, но возникает интересный вопрос: можно ли использовать оптимизационные формулы из задачи классификации? Сначала давайте подумаем, что выдаст алгоритм, если формулу применить без изменений.

В задаче регрессии почти наверняка все значения будут различными. Поэтому для любого сумма в формуле будет состоять из не более чем одного слагаемого, а значит, максимум будет достигаться на соседе с наибольшим весом, то есть на ближайшем соседе. Это означает, что метод всегда вырождается в 1-NN. Это не совсем то, чего мы добиваемся, поэтому давайте немного модифицируем алгоритм.

Давайте сперва подумаем, а для чего вообще в формуле используется индикатор. В задаче классификации индикатор — естественная мера близости двух объектов: если объекты совпадают, то значение , если различаются, то . Проблема в том, что в задаче регрессии объекты являются действительными числами, и для них функция, которая выдаёт отличное от нуля значение лишь в одной точке , — плохая мера близости.

В случае непрерывных значений естественно использовать более гладкие функции для выражения близости. Таким образом, для обобщения формулы на задачу регрессии нам необходимо всего лишь заменить индикатор на некоторую более гладкую функцию. При этом для действительных чисел чаще всего рассматривают не близость, а расстояние между ними, то есть некоторую метрику. Например, в качестве такой метрики можно взять квадрат евклидова расстояния . Отметим, что максимизация близости эквивалентна минимизации расстояния, и получим следующую формулу:

Выбор именно этой функции хорош тем, что у этой оптимизационной задачи есть точное решение, и оно записывается как раз формулой .

Для ядерной регрессии справедливы те же рассуждения про выбор ядра и ширины окна, которые были приведены в прошлом разделе про классификацию.

Влияние ширины окна и вида ядра на вид функции:

Преимущества и недостатки

Сперва поговорим о преимуществах алгоритма.

• Непараметрический, то есть не делает явных предположений о распределении данных.
• Очень простой в объяснении и интерпретации.
• Достаточно точный, хоть и чаще всего уступает градиентному бустингу и случайному лесу в accuracy.
• Может быть использован как для классификации, так и для регрессии.

Несмотря на большие преимущества, алгоритм не лишён и минусов.

• Неэффективный по памяти, поскольку нужно хранить всю обучающую выборку.
• Вычислительно дорогой по той же причине.
• Чувствителен к масштабу данных, а также к неинформативным признакам.
• Для применения алгоритма необходимо, чтобы метрическая близость объектов совпадала с их семантической близостью, чего не всегда просто добиться. Представим, например, что мы решаем задачу нахождения похожих изображений. Мы хотим, чтобы картинки с лесом находились близко друг к другу, однако, если взять любую попиксельную метрику, такие картинки могут быть очень далеки друг от друга. Зачастую для решения этой проблемы вначале обучают представления.

Применение

Из-за своих недостатков алгоритм очень неэффективен в задачах с большим количеством данных. Однако у него всё равно есть много применений в реальном мире. Приведём лишь некоторые из них:

• Рекомендательные системы. Если посмотреть на саму формулировку задачи «предложить пользователю что-то похожее на то, что он любит», то KNN прямо напрашивается в качестве решения. Несмотря на то что сейчас часто используются более совершенные алгоритмы, метод ближайших соседей всё равно применяется в качестве хорошего бейзлайна.
• Поиск семантически похожих документов. Если векторные представления близки друг к другу, то темы документов схожи.
• Поиск аномалий и выбросов. Из-за того что алгоритм запоминает обучающую выборку полностью, ему легко посмотреть, насколько целевой объект похож на все данные, которые он видел.
• Задача кредитного скоринга. Рейтинги двух людей, у которых примерно одинаковая зарплата, схожие должности и кредитные истории, не должны сильно отличаться, поэтому KNN отлично подходит для решения такой задачи.

Вопрос сложности алгоритма неочевиден и требует детального анализа, который будет частично проведён в следующем разделе.

Поиск ближайших соседей

Для того чтобы применять метод ближайших соседей, нужно уметь как-то находить этих самых соседей. С первого взгляда может показаться, что никакой проблемы нет: действительно, можно ведь просто перебрать все объекты из обучающей выборки , посчитать для каждого из них расстояние до тестового объекта и затем найти минимум.

Однако несмотря на то что сложность такого поиска линейная по , она также зависит и от размерности пространства признаков. Если , то сложность такого алгоритма поиска . Если вспомнить, что в типичной задаче машинного обучения количество признаков может быть порядка , а размер выборки и вовсе может исчисляться десятками и сотнями тысяч объектов, то становится ясно, что такая сложность никуда не годится. Проблема осложняется ещё и тем, что данный поиск необходимо выполнять на этапе применения модели, который должен быть быстрым. Всё это означает, что возникает необходимость в более быстрых методах поиска ближайших соседей, чем простой перебор.

Все такие методы можно поделить на две основные группы: точные и приближённые. Последние, как следует из их названия, находят соседей лишь приближённо, то есть найденные объекты хоть и будут действительно близки, но не обязательно будут самыми близкими. В этом разделе мы подробнее рассмотрим методы из каждой группы.

Перед началом обзора стоит сказать, что хоть мы и рассматриваем алгоритмы поиска соседей именно в контексте их использования в KNN, область их применения значительно шире, и она не ограничивается исключительно машинным обучением. Например, на их основе работает любая информационно-поисковая система, от поиска в «Гугле» или «Яндексе» до всем известных алгоритмов «Ютьюба».

Поиск ближайших соседей: точные методы

Точных методов существует довольно мало. Можно сказать, что их, по сути, два.

• Первый — полный перебор с различными эвристиками. Например, можно выбрать подмножество признаков и считать расстояние только по ним. Оно будет оценкой снизу на реальное расстояние, поэтому если оно уже больше, чем до текущего ближайшего объекта, то можно сразу отбросить этот объект и переходить к следующему. Такие эвристики хоть и могут давать некоторый выигрыш по времени, но не улучшат асимптотическую сложность.
• Второй — k-d-деревья, о которых стоит поговорить подробнее.

K-d-деревья

Представим на секунду, что у нас есть всего лишь один признак, то есть объекты выражаются вещественными числами, а не векторами. В этом случае для поиска ближайшего соседа напрашивается всем вам известное бинарное дерево поиска, которое позволяет находить элементы за логарифмическое время. Оказывается, существует аналог данной структуры в многомерном пространстве, который называется k-d-дерево (k-d tree, сокращение от k-dimensional tree).

Как и в обычном дереве поиска, в k-d-дереве каждый узел является объектом обучающей выборки, который особым образом делит пространство на два полупространства. Таким образом, всё пространство оказывается поделено на множество малых областей, и такое деление оказывается очень полезным при поиске ближайших соседей.

Рассмотрим подробнее, как строится такое дерево. Трудность в применении обычного дерева поиска состоит в том, что мы не можем напрямую сравнить два вектора так же, как два вещественных числа. Чтобы эту проблему преодолеть, узлы дерева будут делить пространство лишь по одной оси. При движении вниз по дереву оси, по которым точки делят пространство, циклически сменяют друг друга. Например, в двумерном пространстве корень будет отвечать за деление по x-координате, его сыновья — за деление по y-координате, а внуки — снова за x-координату, и т. д. Посмотрим, как это работает на примере:

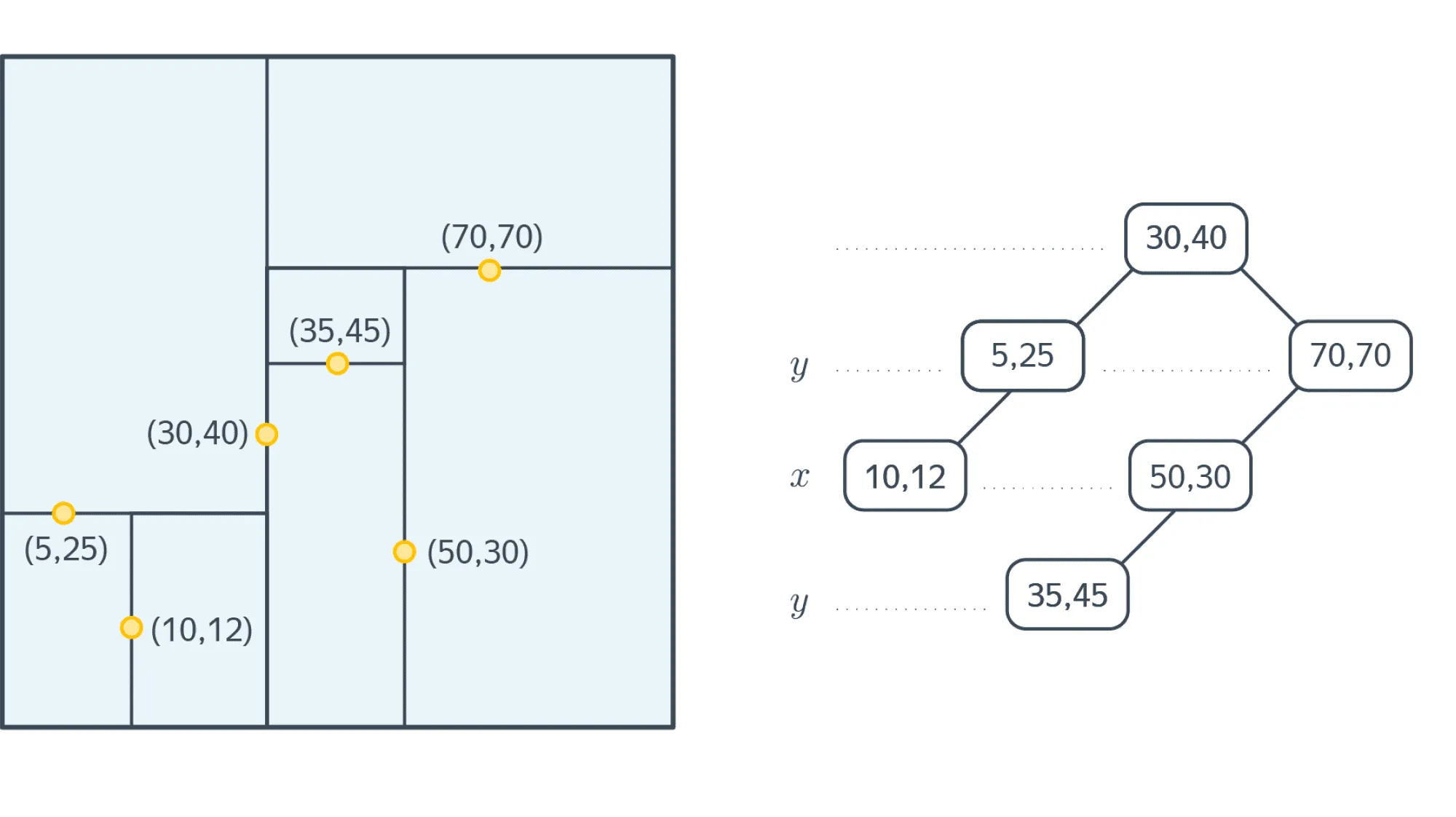
На картинке выше корень делит все точки по оси х: слева оказываются точки, у которых , а справа — те, у которых . Аналогично левый сын корня делит своё поддерево по оси y: слева оказываются точки, у которых , а справа — те, у которых .

Остаётся вопрос — как выбирать точки, которые будут делить пространство пополам? Чтобы дерево было сбалансированным, нужно находить точку с медианой, соответствующей уровню поддерева координаты. На практике часто ограничиваются выбором случайной точки или любой эвристикой по приближённому поиску медианы (например, медиана некоторого подмножества точек). Это позволяет ускорить построение дерева, но убирает все гарантии на его сбалансированность.

Добавлять новые точки можно так же, как и в одномерном дереве поиска. Спускаясь по дереву, можно однозначно определить лист, к которому нужно подвесить новую точку, чтобы не нарушить все свойства дерева. При добавлении большого количества точек, однако, дерево может перестать быть сбалансированным, и нужно проводить ребалансировку. Также существуют варианты k-d-деревьев, которые сохраняют сбалансированность при добавлении / удалении точек.

Поговорим теперь про то, как же находить ближайших соседей с помощью такого дерева. Будем производить обход дерева в глубину с двумя модификациями.

• Во-первых, будем запоминать наиболее близкую точку. Это позволит не заходить в поддеревья, задающие области, которые заведомо дальше, чем текущая наиболее близкая точка, поэтому не имеет смысла искать в них ближайших соседей.
• Во-вторых, будем прежде всего обходить те поддеревья, которые задают наиболее близкие области, а значит, с большей вероятностью содержат ближайшего соседа.

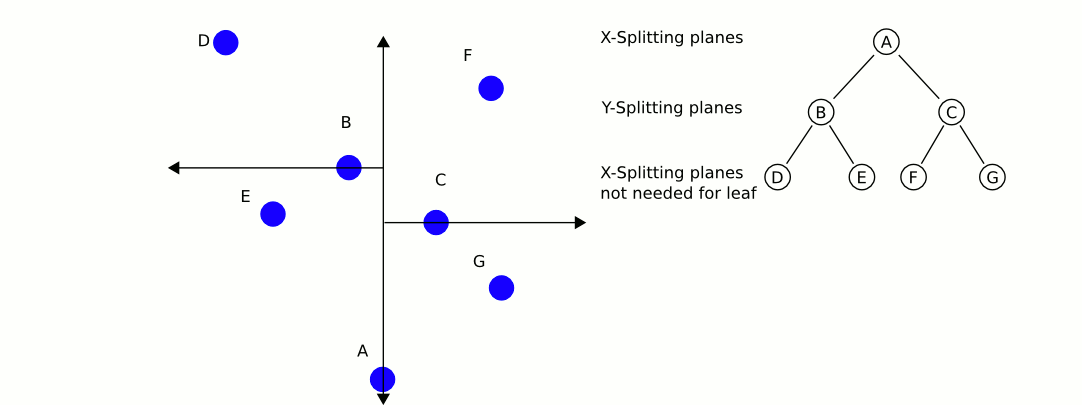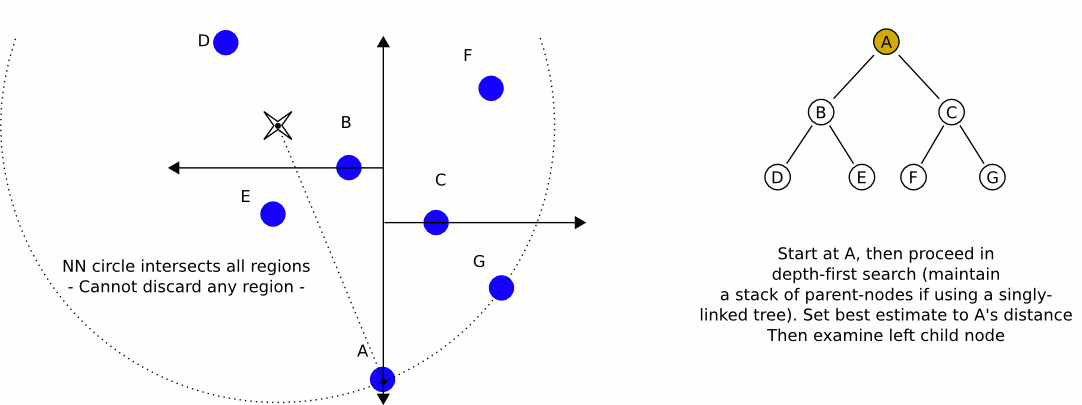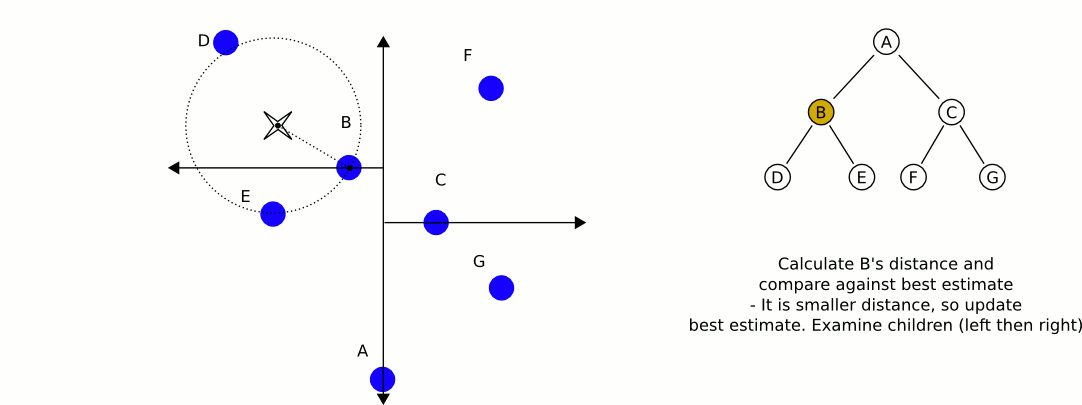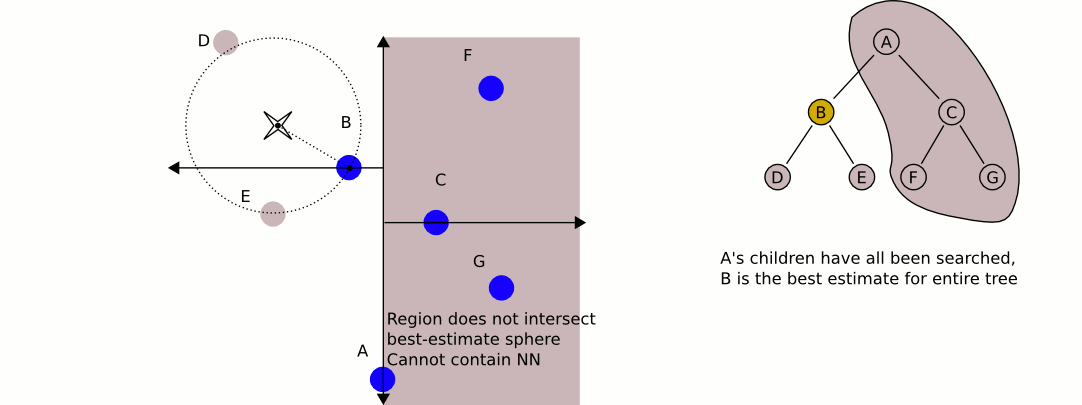
Сложность метода по размеру обучающей выборки в среднем равна при равномерном распределении точек. При большой размерности пространства, однако, алгоритму приходится посещать больше ветвей дерева, чтобы найти ближайших соседей. Например, если , то сложность становится примерно такой же, как и в случае полного перебора. В общем случае считается, что для того чтобы асимптотика действительно была логарифмической, нужно, чтобы . Поэтому уже при количестве признаков порядка сотни алгоритм не даёт существенных преимуществ перед полным перебором.

Почитать по теме:

• Хорошая презентация, объясняющая структуру и поиск соседей.
• Балансировка деревьев.

Поиск ближайших соседей: приближённые методы

Почти всегда находить именно самых близких соседей необязательно. Например, в задаче подбора рекомендаций фильмов пользователю чаще всего не нужны наиболее похожие картины, достаточно, к примеру, 10 из 15 наиболее близких. Поэтому, чтобы ускорить процесс поиска соседей, используют приближённые методы. Разберём основные идеи, которые применяются в таких методах.

Random projection trees

Алгоритмы, основанные на деревьях, очень часто применяются в задачах поиска соседей. Идея всех таких методов заключается в итеративном разделении пространства случайными гиперплоскостями и построении на базе этого разделения дерева, в листах которого содержится малое число объектов.

Одним из наиболее ярких представителей этого семейства является Annoy — алгоритм, который используется Spotify для рекомендаций музыки. Задача подобных рекомендательных систем довольно простая — нужно посоветовать пользователю композиции, которые он ещё не слушал, но которые при этом с высокой вероятностью ему понравятся. Простая и рабочая идея — предлагать композиции, похожие на те, которые он уже слушает. Здесь на помощь как раз и приходят методы поиска ближайших соседей.

Annoy в какой-то степени похож на k-d-деревья. Сначала выбираются два случайных объекта обучающей выборки и проводится гиперплоскость, симметрично их разделяющая. Затем для каждого полученного полупространства итеративно запускается такая же процедура, которая продолжается до тех пор, пока в каждой области будет не более объектов ( — гиперпараметр).

Таким образом задаётся бинарное дерево с глубиной порядка в среднем.

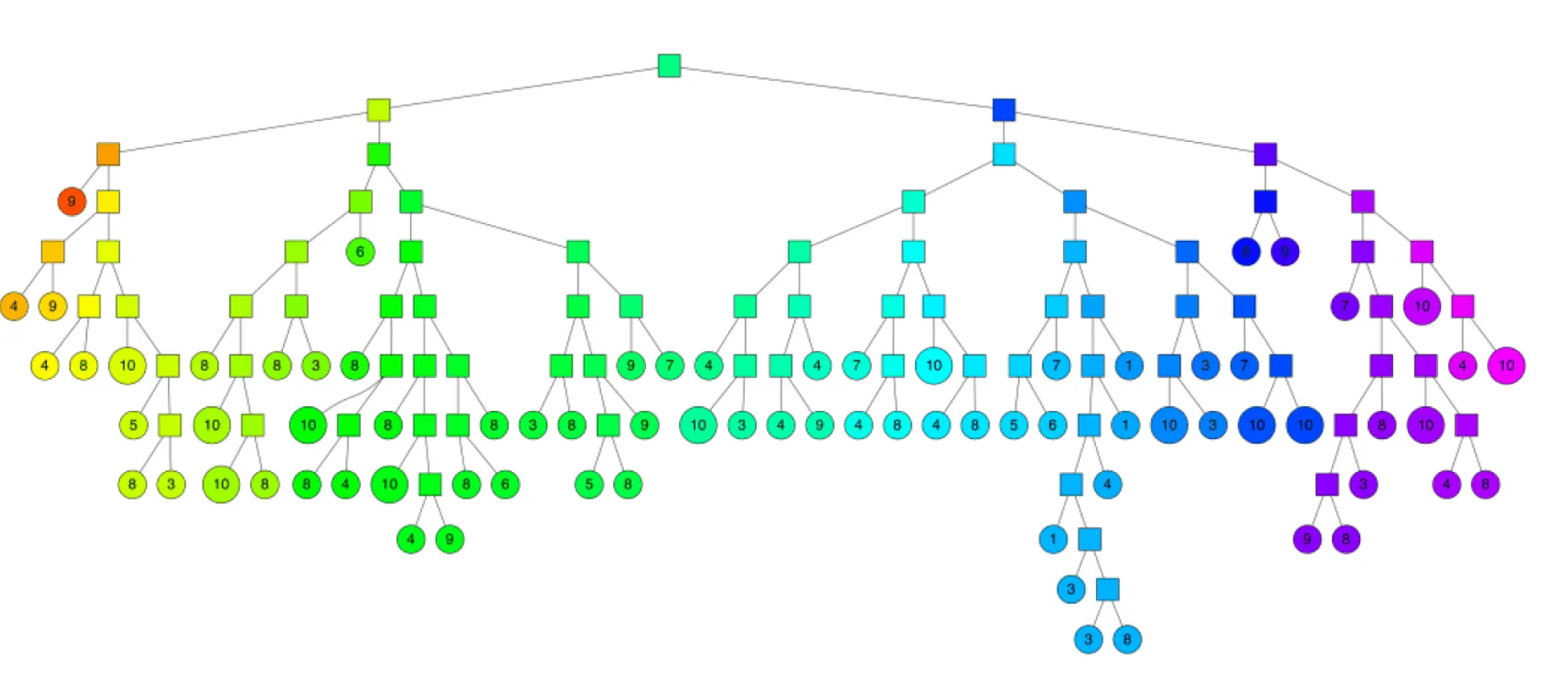
Спускаясь по этому дереву, можно найти область, в которой лежит целевой объект и некоторое количество близких к нему элементов обучающей выборки. Проблема в том, что это не обязательно будут самые близкие объекты, поэтому для увеличения точности составляется лес из таких деревьев и берётся объединение соответствующих целевому объекту областей.

Чем больше таких деревьев берётся, тем более точным будет результат, но придётся тратить большее время на его поиск.

Преимущество алгоритма — простота нахождения компромисса между скоростью работы и точностью с помощью тюнинга гиперпараметров. К минусам можно отнести то, что алгоритм плохо параллелится и переносится на GPU, не работает эффективно с батчами, а также то, что для добавления новой точки в обучающую выборку придётся перезапускать процедуру с самого начала.

Почитать по теме:

• Отличная статья с иллюстрациями и подробным описанием алгоритма.

Locality-sensitive hashing (LSH)

Предположим, что мы можем построить такую хеш-функцию, которая переводит близкие объекты в один бакет. Тогда близких соседей целевого объекта можно найти, посчитав его хеш и посмотрев на коллизии. Оказывается, такие хеш-функции существуют, и на этой идее основано несколько алгоритмов, которые объединяются названием Locality-sensitive hashing (LSH). К этому классу алгоритмов относится, например, FAISS, используемый Facebook.

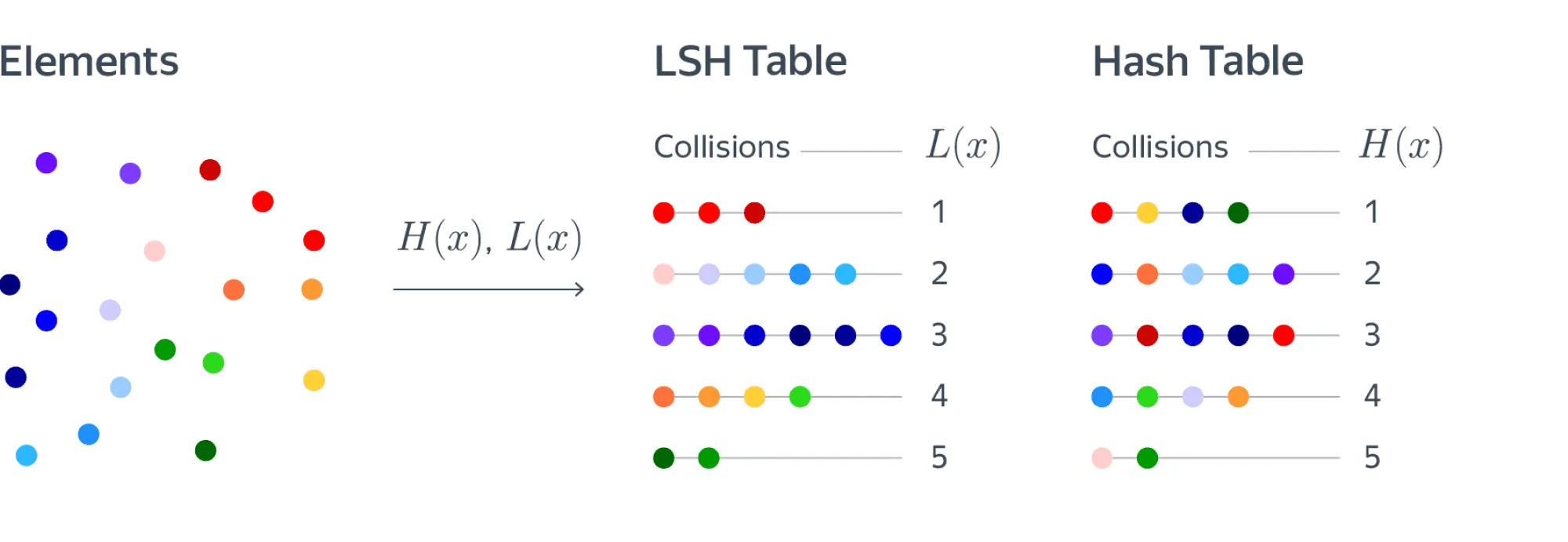
Определим формально семейство хеш-функций, которое мы хотим использовать. Нам нужно, чтобы вероятность коллизии на близких объектах была высокая, а на далёких — низкая. Назовём семейство хеш-функций -чувствительным, если для любой :

• для вероятность коллизии ;
• для вероятность коллизии .

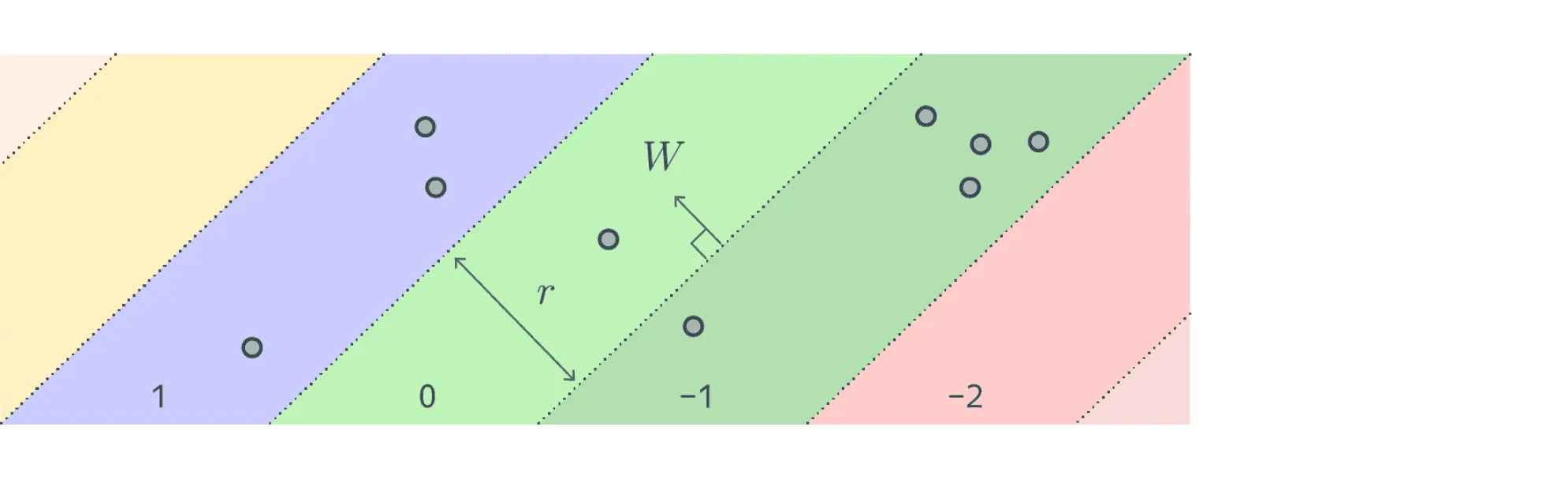
Формулы могут выглядеть сложными, но это всего лишь формализация нашей интуиции. Картинка ниже поясняет определение: для близких красных объектов в шаре радиусом вероятность коллизии больше , для далёких синих объектов на расстоянии больше вероятность коллизии меньше , а про серые объекты в слое между и мы ничего не знаем.

Для каждой функции расстояния, используемой в задаче, существует своё подходящее семейство хеш-функций. Например, для евклидовой и манхэттенской метрик используются случайные проекции, где хеш-функция имеет следующий вид:

где и — случайные параметры, а выбирается пользователем. выбирается равномерно из отрезка , а генерируется либо из нормального распределения, что соответствует евклидовой метрике, либо из распределения Коши — для манхэттенской метрики.

По сути, такая функция разбивает всё пространство на слои в направлении вектора . Параметр при этом задаёт ширину слоя.

На практике при использовании лишь одной хеш-функции разница между и оказывается очень маленькой, поэтому применяют различные методы для её увеличения.

• Первый способ — уменьшать размер бакетов в хеш-таблице путём использования композиции разных хеш-функций из одного семейства . Преимущество этого способа как раз хорошо видно на примере случайных проекций. При использовании лишь одной хеш-функции бакетами являются слои бесконечного объёма. Однако при использовании композиции размером, как минимум равным количеству признаков , из-за случайности выбора вектора бакеты почти наверное станут замкнутыми фигурами с конечным объёмом.
• Второй способ повышения эффективности алгоритма — использовать несколько хеш-таблиц и искать соседей среди коллизий в каждой из них. На практике используют оба метода сразу, подбирая и — количество хеш-таблиц как гиперпараметры.

К плюсам алгоритма можно отнести хорошие теоретические гарантии на сублинейное время и, как и в Annoy, простой поиск компромисса между точностью и скоростью работы. Минусами можно назвать высокую потребность в памяти, плохую адаптируемость под GPU, а также тот факт, что, несмотря на теоретические гарантии в среднем, на практике алгоритм может работать даже чуть дольше полного перебора из-за того, что, помимо самого поиска, требуется искать хеши объектов.

Почитать по теме:

• Отличная статья с объяснением в иллюстрациях и примерами хеш-функций для других метрик.
• Ещё одна статья, в которой шаг за шагом выводится алгоритм на примере расстояния Жаккара.

Proximity graphs & Hierarchical navigable small world (HNSW)

Следующий класс алгоритмов основан на построении специального графа близости (proximity graph) на объектах выборки и дальнейшем жадном поиске по этому графу. Алгоритмы этого семейства сейчас считаются state-of-the-art (SotA) для многих задач.

Рассмотрим подробнее этот класс алгоритмов на примере одного из наиболее популярных из них под названием Navigable small world (NSW). Идея его в следующем: на данных строится граф (он также называется NSW), который удовлетворяет двум следующим свойствам:

1. Между любыми двумя точками существует короткий путь, или, более формально, матожидание числа кратчайшего пути между двумя случайно выбранными вершинами растёт как .
2. Средняя степень вершины мала.

На первый взгляд может показаться, что тяжело выполнить одновременно оба свойства, но на самом деле большая часть графов в реальном мире являются NSW-графами. Самый простой пример — это известное правило шести рукопожатий: любые два случайных человека соединены короткой последовательностью личных контактов длиной не более шести, несмотря на то, что количество знакомых у среднего человека (–) мало по сравнению с населением Земли.

В таких графах существует очень простой метод поиска соседей. Нужно выбрать случайную точку, среди её соседей выбрать того, который ближе всего к целевому объекту, и повторить процедуру уже для него. Показано, что такой жадный поиск имеет полилогарифмическую асимптотику.

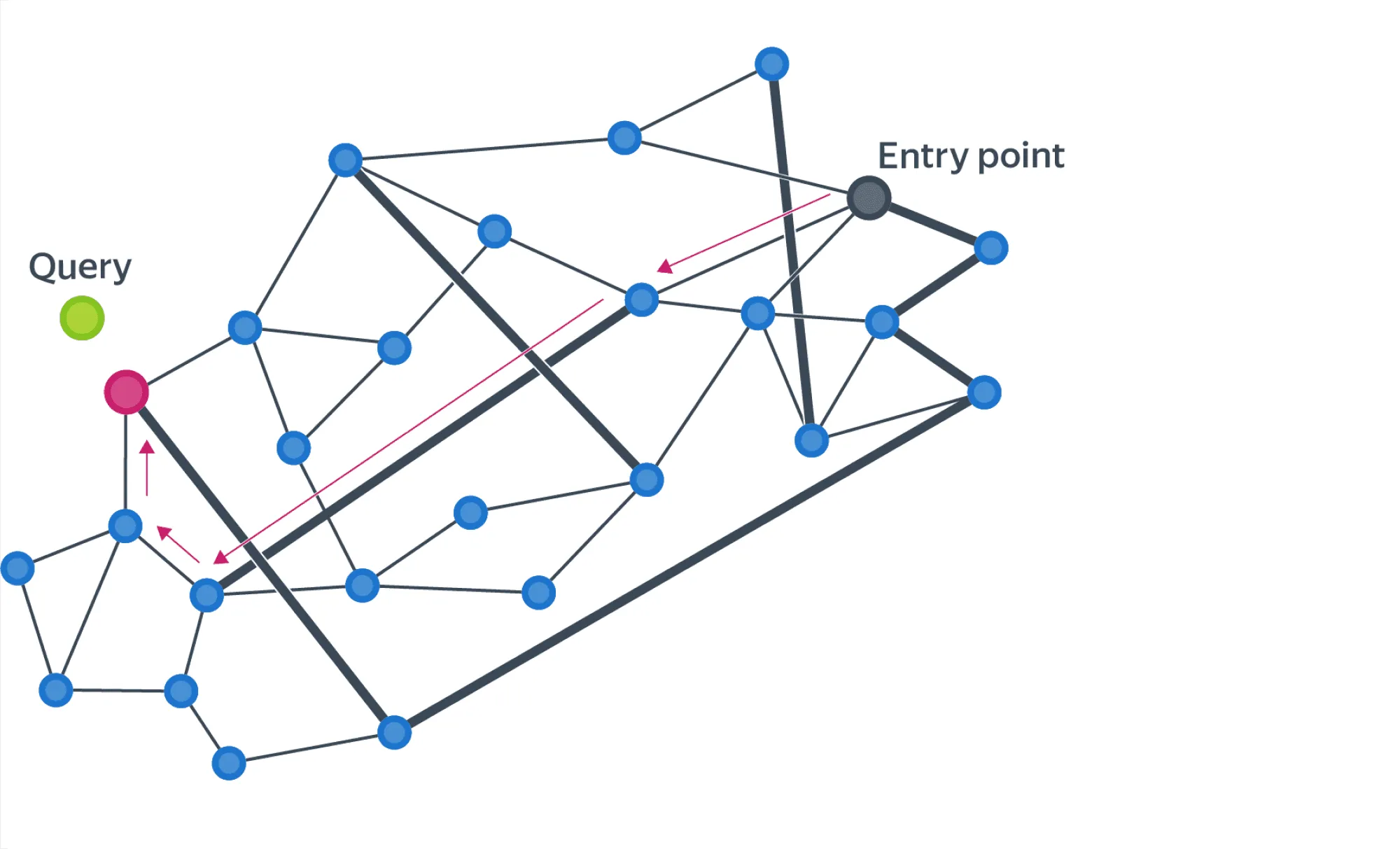
Проблема такого подхода в том, что можно попасть в плотный кластер и очень долго оттуда выбираться. Для решения этой проблемы используется иерархия NSW, или Hierarchical navigable small world (HNSW). Исходный граф является нулевым слоем. Каждый следующий слой строится в два шага:

1. Каждая вершина текущего слоя попадает в следующий с некоторой вероятностью .
2. На всех вершинах, попавших в новый слой, строится NSW.

По построению количество слоёв будет .

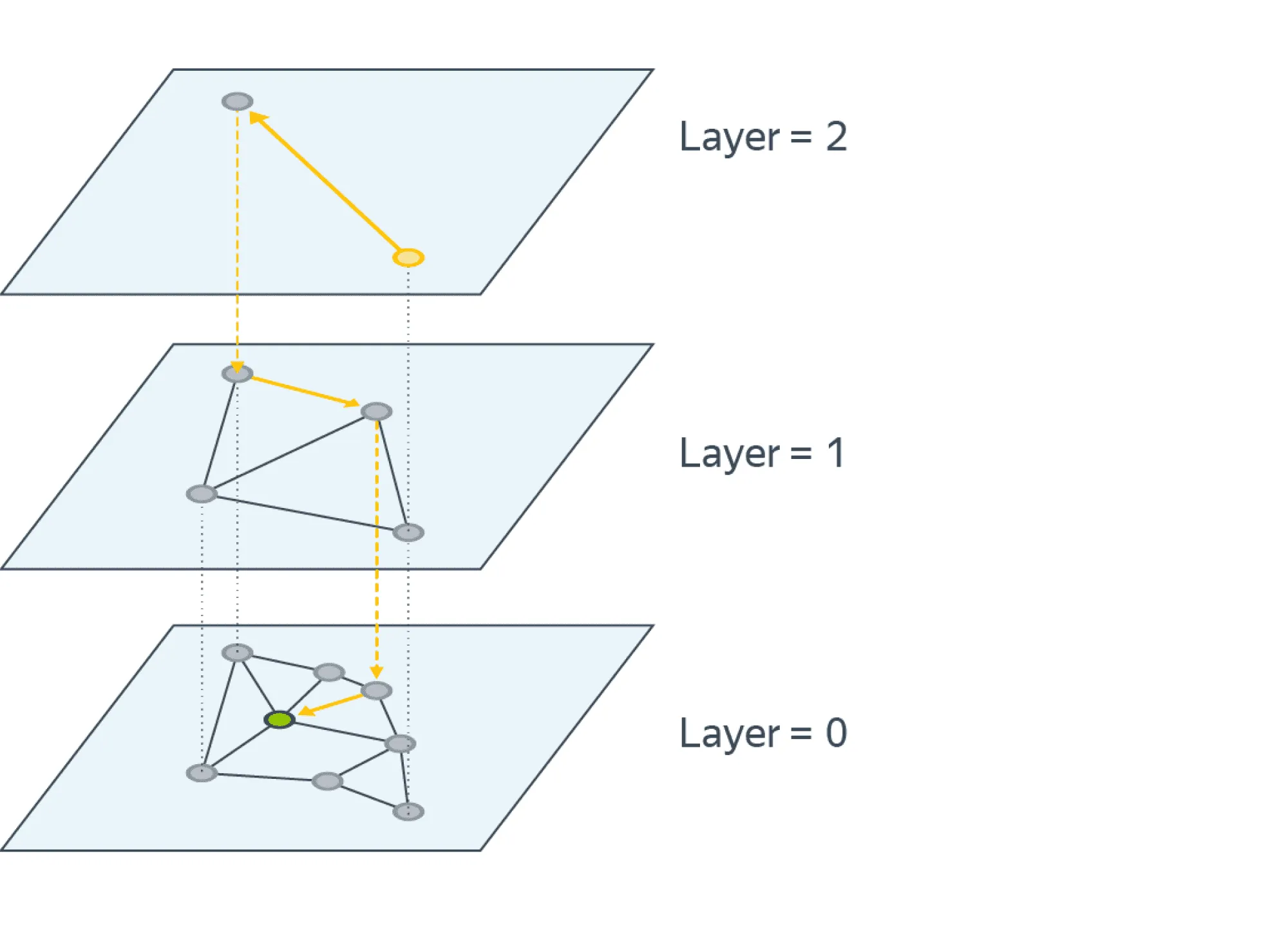
Поиск начинается в самом верхнем слое. После нахождения ближайшей к целевому объекту вершины спускаемся на слой ниже и начинаем поиск из этой вершины. Повторяем процедуру, пока не спустимся до нулевого слоя. Таким образом, на каждом слое мы всё больше уточняем наш ответ. Стоит отметить, что для ускорения работы иногда поиск останавливают не при нахождении ближайшей вершины, а раньше, используя критерии остановки.

Интуитивно легко понять, почему такая иерархическая структура решает проблему плотных кластеров: в верхних слоях вершин мало, а расстояния между ними в среднем большие, а значит, таких кластеров там почти нет. Поэтому, попадая в нижний слой, мы чаще всего оказываемся уже в нужном кластере и просто уточняем результат работы алгоритма.

HNSW, так же как и рассмотренные ранее приближённые методы, позволяет искать трейд-офф между точностью и скоростью работы. Плюс ко всему на реальных данных он часто работает лучше других методов и сейчас считается SotA. Однако этот способ поиска не лишён и недостатков. Главный заключается в том, что нельзя добавлять точки в обучающую выборку без перестройки структуры. Помимо этого, он довольно требователен по памяти из-за того, что для каждого слоя приходится хранить как вершины, которые в него входят, так и связи между этими вершинами.

Подробнее — в оригинальной статье.

В завершение стоит сказать, что не существует универсального метода поиска соседей — каждый из описанных методов может быть лучше других в определённой задаче. К тому же, несмотря на то что приближённые методы имеют лучшую асимптотику, многие из них плохо переносятся на GPU. Из-за этого на практике полный перебор бывает быстрее любого из таких приближённых методов.