6.4. Графовые нейронные сети

Введение

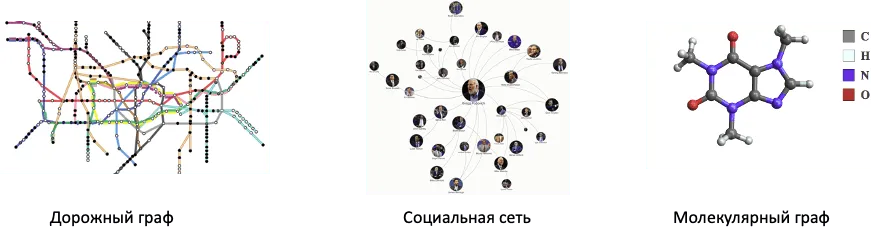
Наряду с обработкой табличных, текстовых, аудио данных и изображений, в глубинном обучении довольно часто приходится решать задачи на данных, имеющих графовую структуру. К таким данным относятся, к примеру, описания дорожных и компьютерных сетей, социальных графов и графов цитирований, молекулярных графов, а также графов знаний, описывающих взаимосвязи между сущностями, событиями и абстрактными категориями.

В этом параграфе мы с вами познакомимся с основными задачами, которые возникают при обработке графов, а также поговорим о графовых свертках и графовых нейронных сетях — специальном классе обучаемых преобразований, способных принимать в качестве входа графы и решать задачи на них.

Описание графовых данных

Граф принято представлять двумя множествами: множеством , содержащим вершины и их признаковые описания, а также множеством , содержащим связи между вершинами (то есть рёбра) и признаковые описания этих связей. Для простоты математических выкладок и изложения дальнейшего материала давайте считать, что мы всегда работаем с ориентированными графами. Если граф содержит ненаправленное ребро, мы его заменяем на пару направленных ребер. Кроме того, давайте обозначать окрестность вершины как .

Графовые данные довольно разнообразны. Они могут отличаться между собой в следующих моментах:

• По размеру, т.е. количеству вершин и/или ребер.
• По наличию признаковых описаний вершин и рёбер. В зависимости от решаемой задачи, графы могут содержать информацию только в вершинах, только в ребрах, либо же и там и там.
• Кроме того, графы могут быть гомо- и гетерогенными — в зависимости от того, имеют ли вершины и ребра графа одну природу либо же нет.

Например, социальные графы содержат огромное количество вершин и ребер, часто измеряющееся в тысячах, содержат информацию в вершинах и очень редко в ребрах, а также являются гомогенными, так как все вершины имеют один тип. В то же время, молекулярные графы — это пример графов с, как правило, средним количеством вершин и ребер; вершины и связи в молекулярных графах имеют признаковое описание (типы атомов и ковалентных связей, а также информацию о зарядах и т.п.), но при этом также являются гомогенными графами. К классу гетерогенных графов относятся, например, графы знаний, описывающие некоторую систему, различные сущности в ней и взаимодействия между этими сущностями. Вершины (сущности) и связи (ребра) такого графа могут иметь различную природу: скажем, вершинами могут быть сотрудники и подразделения компании, а рёбра могут отвечать отношениям «Х работает в подразделении Y», «X и Z коллеги» и так далее.

Задачи на графах

Разнообразие графовых данных закономерно породило множество разнообразных задач, которые решаются на этих данных.

Среди них можно встретить классические постановки классификации, регрессии и кластеризации, но есть и специфичные задачи, не встречающиеся в других областях — например, задача восстановления пропущенных связей внутри графа или генерации графов с нужными свойствами. Однако даже классические задачи могут решаться на различных уровнях: классифицировать можно весь граф (graph-level), а можно отдельные его вершины (node-level) или связи (edge-level).

Так, в качестве примера graph-level задач можно привести классификацию и регрессию на молекулярных графах. Имея датасет с размеченными молекулами, можно предсказывать их принадлежность к лекарственной категории и различные химико-биологические свойства.

На node-level, как правило, классифицируют вершины одного огромного графа, например, социального. Имея частичную разметку, хочется восстановить метки неразмеченных вершин. Например, предсказать интересы нового пользователя по интересам его друзей.

Часто бывает такое, что граф приходит полностью неразмеченным и хочется без учителя разделить на компоненты. Например, имея граф цитирований, выделить в нем подгруппы соавторов или выделить области исследования. В таком случае принято говорить о node-level кластеризации графа.

Наконец, довольно интересна задача предсказания пропущенных связей в графе. В больших графах часто некоторые связи отсутствуют. Например, в социальном графе пользователь может добавить не всех знакомых в друзья. А в графе знаний могут быть проставлены только простые взаимосвязи, а высокоуровневые могут быть пропущены.

В конце, хотелось бы отметить очень важные особенности всех задач, связанных с графами. Алгоритмы решения этих задач должны обладать двумя свойствами.

• Во-первых, графы в датасетах, как правило, могут отличаться по размерам: как по количеству вершин, так и по количеству связей. Алгоритмы решения задач на графах должны уметь принимать графы различных размеров.
• Во-вторых, алгоритмы должны быть инварианты к перестановкам порядка вершин. То есть если взять тот же граф и перенумеровать его вершины, то алгоритмы должны выдавать те же предсказания с учетом этой перестановки.

Графовые нейронные сети

Развитие глубинного обучения повлияло на подходы к решению задач на графовых данных. Был предложен концепт графовых нейронных сетей, которые в последнее время либо полностью заменили классические алгоритмы обработки графов, либо породили мощные синергии с этими алгоритмами.

Графовые нейронные сети по принципу работы и построения идейно очень похожи на сверточные нейронные сети. Более того, забегая немного вперед, графовые нейроные сети являются обобщением сверточных нейронных сетей.

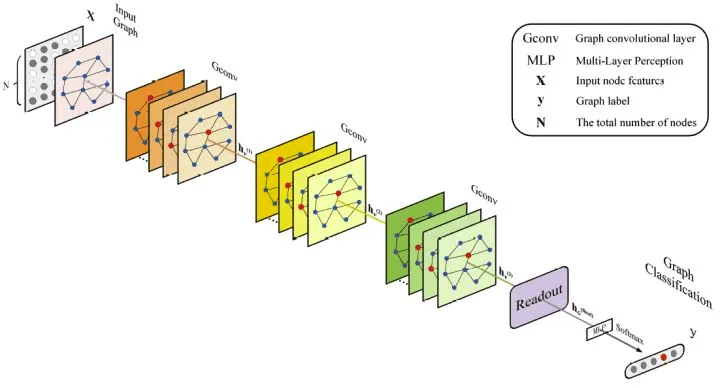
На вход графовой нейронной сети подается граф. В отличие от сверточных нейронных сетей, которые требуют, чтобы все картинки в батче были одинакового размера, графовые нейронные сети допускают разные размеры у объектов батча. Кроме того, в отличие от картинок, у которых информация довольно однородна (это, как правило, несколько цветовых каналов) и хранится в пикселях, у графов информация может также храниться в вершинах и/или ребрах. Причем в одних задачах информация может быть только в вершинах, в других только в ребрах, а в третьих и там, и там. Сама информация может быть довольно разнородной: это могут быть и вещественные значения, и дискретные значения, в зависимости от природы графа и от типа решаемой задачи. Поэтому, довольно часто первым слоем в графовых нейронных сетях идут Embedding слои, которые переводят дискретные токены в вещественные векторы.

Однако, сама суть работы у графовых и сверточных сетей совпадает. В графовой нейронной сети по очереди применяются слои, которые собирают информацию с соседей и обновляют информацию в вершине. То же самое делают и обычные свертки. Поэтому такие слои и называются графовыми свертками. Графовая свертка принимает на вход граф со скрытыми состояниями у вершин и ребер и выдает тот же граф, но уже с обновленными более информативными скрытыми состояниями.

В отличие от сверточных нейронных сетей, при обработке графа pooling слои вставляют редко, в основном в graph-level задачах, при этом придумать разумную концепцию графового пулинга оказалось нелегко. Если вам станет интересно, вы можете познакомиться с несколькими вариантами графовых пулингов в следующих статьях:

• Learning Spectral Clustering
• Kernel k-means, Spectral Clustering and Normalized Cuts
• Weighted Graph Cuts without Eigenvectors

В большинстве же архитектур пулинги не используются, и структура графа на входе и выходе графовой нейронной сети совпадает.

Полученная после череды сверток информация с вершин и ребер в конце обрабатывается с помощью полносвязных сетей для получения ответа на задачу. Для node-level классификации и регрессии полносвязная сеть применяется к скрытым состояниям вершин , а для edge-level, соответственно, к скрытым состояниям ребер . Для получения ответа на graph-level уровне информация с вершин и ребер сначала агрегируется с помощью readout операции. На месте readout операции могут располагаться любые инвариантные к перестановкам операции: подсчет максимума, среднего или даже обучаемый self-attention слой.

Как говорилось ранее, графовые нейронные сети являются обобщением сверточных. Если представить пиксели изображения вершинами графа, соединить соседние по свертке пиксели ребрами и предоставить относительную позицию пикселей в информации о ребре, то графовая свертка на таком графе будет работать так же, как и свертка над изображением.

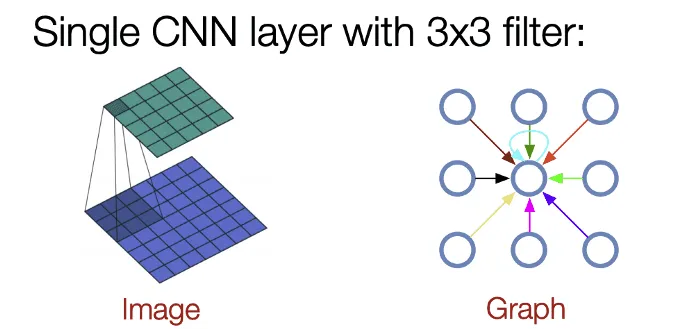
К графовым нейронным сетям, как и к сверточным, применим термин receptive field. Это та область графа, которая будет влиять на скрытое состояние вершины после N сверток. Для графов receptive field после N графовых сверток — это все вершины и ребра графа, до которых можно дойти от фиксированной вершины не более чем за N переходов. Знание receptive field полезно при проектировании нейронной сети - имея представление о том, с какой окрестности вершины надо собрать информацию для решения задачи, можно подбирать нужное количество графовых сверток.

Многие техники стабилизации обучения и повышения обобщаемости, такие как Dropout, BatchNorm и Residual Connections, применимы и к графовым нейронным сетям. Однако стоит помнить про их особенности. Эти операции могут независимо применяться (или не применяться) к вершинам и ребрам. Так, если вы применяете Dropout, то вы вправе поставить для вершин и для рёбер различные значения dropout rate. Аналогично и для Residual Connections - они могут применяться только для вершин, только для ребер или же и там и там.

Кроме того, стоит иметь ввиду, что графы различных размеров будут неравноценно влиять на среднее и дисперсию в BatchNorm слое. Более стабильной альтернативой BatchNorm в обработке графов, например, являются LayerNorm и GraphNorm, которые производят нормировку активаций по каждому графу независимо.

LayerNorm, по сути, применяет BatchNorm для каждого графа:

A вот GraphNorm содержит несколько обучаемых параметров и является более гибким вариантом нормализации:

Парадигмы построения графовых сверток

Важно отметить, что в отличие от свертки, применяемой для изображений, являющейся четко определенной операцией, графовая свертка представляет собой именно концепт, абстрактную операцию, обновляющую скрытые представления объектов графа, используя доступную информацию с соседей и ребер. На практике, конкретный механизм графовой свертки разрабатывается для конкретной задачи, и различные реализации графовых сверток могут очень сильно отличаться между собой. И если зайти на сайты популярных фреймворков глубинного обучения на графах (например, PyG), то можно обнаружить десятки различных реализаций графовых сверток.

Во-первых, графовые свертки отличаются между собой по тому набору информации, которые они могут использовать. Есть свертки, которые используют только скрытые представления вершин, игнорируя информацию на ребрах. Существуют свертки, которые по разному обрабатывают информацию от ребер различного типа. А есть свертки, которые используют информацию с ребер и вершин, обновляя одновременно и те и другие.

Во-вторых, и что более важно, графовые свертки можно разделить на два семейства, которые отличаются математической парадигмой, в которой они работают. Есть spatial (пространственный) и spectral (спектральный) подходы. Пространственные свертки основываются на message-passing парадигме, в то время как спектральные работают с графовым лапласианом и его собственными векторами.

На практике, спектральные свертки чаще применяются и показывают лучшие результаты в задачах связанных с обработкой одного большого графа, где важно понимать относительное месторасположение вершины в этом большом графе. Например, графа соцсетей или графа цитирований. Пространственные свертки показывают хорошие результаты в остальных задачах, где для решения задачи важно находить локальные подструктуры внутри графа.

Несмотря на принципиальную противоположность этих двух подходов, активно предпринимаются попытки их совмещения в одну парадигму, например, в этой работе.

Давайте разберемся с этими двумя парадигмами.

Пространственная парадигма

Пространственная (spatial) парадигма основывает на алгоритме передачи сообщений (message passing) между вершинами графа.

Концепт этого подхода заключается в следующем - каждая вершина графа имеет внутреннее состояние. Каждую итерацию это внутреннее состояние пересчитывается, основываясь на внутренних состояниях соседей по графу. Каждый сосед влияет на состояние вершины, так же как и вершина влияет на состояния соседей.

Итерация работы Message passing подхода для одной вершины можно описать следующим абстрактным алгоритмом. Для каждой вершины собираются все тройки состоящие из скрытых представлений текущей вершин и ее соседа , а также из типа ребра ,соединяющего текущую вершину и её соседа. Ко всем этим тройкам применяется обучаемое преобразование (от слова message), которая считает сообщение — информацию, которая идет от соседа к вершине. Посчитанные сообщения агрегируются в одно, обозначаемое . Сообщения могут быть сагрегированы любой ассоциативной операцией, например взятием поэлементного минимума, максимума или среднего. Далее, агрегированное сообщение и текущее внутреннее состояние вершины подаются на вход обучаемой операции (от слова update), которая обновляет внутреннее состояние вершины.

Конкретные имплементации операций непосредственно зависят от алгоритма и той задачи, которую он решает.

Одним из самых известных классических алгоритмов, построенных на пространственной парадигме, является PageRank. Алгоритм PageRank проходит по графу веб страниц и выставляет каждой веб-странице значение ее "важности" , которое впоследствии можно использовать для ранжирования поисковой выдачи. Формула подсчета PageRank выражается через коэффициент затухания , а также значения PageRank соседей вершины и количество исходящий ссылок из этих соседей следующим образом:

В такой постановке операции подсчета сообщений и операции обновления имеют следующий вид:

Графовые свертки, работающие на парадигме передачи сообщений, как правило делают и обучаемыми преобразованиями.

Рассмотрим несколько конкретных примеров архитектур.

GraphSAGE

Свертка GraphSAGE работает по следующему принципу. Для каждой вершины вычисляется набор скрытых представлений соседних вершин , из которых идут связи в текущую. Далее, собранная информация агрегируется с помощью некоторой коммутативной операции в вектор фиксированного размера. В качестве операции агрегации авторы предлагают использовать операции взятия средних или максимальных значений скрытых представлений объектов из набора. Далее агрегированный вектор объединяется со скрытым представлением вершины , они домножаются на обучаемую матрицу и к результату умножения поэлементно применяется сигмоида. Обучаемые параметры данного слоя, как и в случае GCN, содержат только одну матрицу.

Данная свертка использует только скрытые представления вершин, однако уделяет больше внимания локальному окружению вершины, нежели её глобальному положению во всем графе. Авторы показали высокое качество данной архитектуры в задачах, связанных с выучиванием представлений вершин, однако использование данной свертки можно встретить и в других задачах, связанных с обработкой графов, не содержащих дополнительной информации о рёбрах.

GAT

Свертка GAT (Graph ATtention) является развитием идеи GraphSAGE. В качестве механизма агрегации эта архитектура предлагает использовать механизм внимания, у которого матрицы преобразования для ключей, значений и запросов совпадают и обозначены в формуле буквой . Как и в GraphSAGE, агрегированное сообщение проходит через сигмоиду, но не домножается перед этим на обучаемую матрицу.

Здесь act — некоторая функция активации. Как и в случае механизма внимания для последовательностей, в момент обновления представления для вершины attention «смотрит» на все остальные вершины и генерирует веса , которые указывают, информация из каких вершин «важнее» для нас.

Благодаря мощности и гибкости механизм внимания, эта свертка показала отличные результаты на множестве задач и является одной из самых популярных сверток. По умолчанию, эта свертка, как и GraphSAGE, использует только признаки вершин, однако, в некоторых проектах можно встретить модификации свертки, в которых механизм внимания учитывает ещё и для информацию ребер.

RGCN

Наконец, есть специально разработанные свертки для обработки графов, ребра которых могут быть нескольких типов. Одна из них называется RGCN (Relational Graph Convolutional Networks). Она суммирует скрытые представления соседей, однако каждое представление соседа домножается на матрицу, зависящую от типа ребра, которое соединяет соседа с текущей вершиной. Если в графе присутствует ребра типов, то данная свертка будет учить матриц - по одной для каждого типа связи.

Спектральная парадигма

Противоположностью пространственной парадигме является спектральная (spectral) парадигма. В своей постановке спектральная парадигма опирается на анализ процесса диффузии сигнала внутри графа и анализирует матрицы, описывающих граф — матрицу смежности и матрицу, которая называется Лапласианом графа.

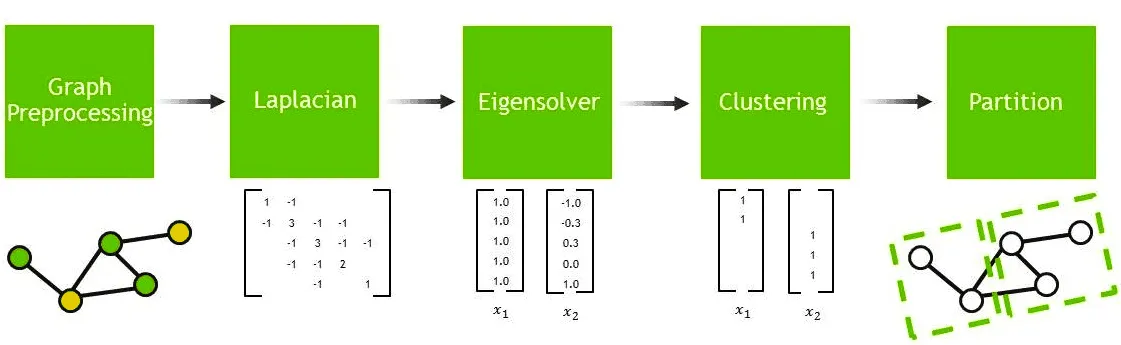
Лапласиан графа — это матрица , где — диагональная матрица, хранящая в -й диагональной ячейке количество исходящих из -й вершины рёбер, а — матрица смежности графа, -й элемент которой равен числу рёбер, соединяющих -ю и -ю вершину.

Лапласиан графа имеет неотрицательные собственные значения. Количество нулевых собственных значений всегда совпадает с количеством компонент связности. Потрясающим свойством Лапласиана является то, что его собственные векторы, соответствующие положительным собственным значениям, в порядке возрастания собственных значений, описывают разрезы графа — его разделения пополам таким образом, чтобы между разделенным половинами было как можно меньше ребер.

Так, собственный вектор, соответствующий наименьшему положительному собственному значению, будет описывать кластеризацию графа на два подграфа. Все индексы, соответствующие положительным элементам вектора задают вершины, которые должны оказаться в первом кластере, а отрицательные элементы будут соответствовать вершинам, которые должны оказаться во втором кластере.

Этим свойством Лапласиана графа пользуются для того, чтобы проводить кластеризацию графа без учителя. Для этого надо:

1. Посчитать Лапласиан матрицы
2. Посчитать собственных векторов, соответствующих наименьшим собственным значениям
3. Сформировать из них матрицу размера , каждая строка которой описывает вершину признаками
4. Кластеризовать объекты, описываемые этой матрицей (например, c помощью K-Means)

Таким образом, спектральный подход отлично подходит для того, чтобы находить в графе компоненты, вершины которых связаны друг с другом и имеют похожие свойства.

GCN

Свертка GCN, основанная на спектральной парадигме, использует только скрытые состояния вершин и матрицу смежности — она учитывает лишь наличие или отсутствие ребра в графе, но не признаки ребер.

С математической точки зрения, GCN очень проста и представляет собой один шаг итеративного процесса поиска собственных значений Лапласиана графа: мы берем скрытые представления вершин и домножаем их на нормированную матрицу смежности — матрицу , домноженную слева и справа на матричный корень матрицы . Этот шаг применяется ко всем каналам скрытого представления вершины. После этого шага, обновленные скрытые представления ещё домножаются на обучаемую матрицу :

Здесь — это матрица размера (число вершин)(длина вектора представления), то есть к каждому «каналу» представлений свёртка применяется отдельно. Если же мы хотим работать с несколькими каналами, то есть вместо у нас матрица размера (число вершин)(число каналов), и ещё добавить нелинейность , формула переписывается следующим образом:

Авторы данной свертки показали отличное качество работы в задачах классификации вершин графов цитирования и графа знаний. Однако, различные модификации данной свертки применяются и в других задачах, например, для выучивания векторных представлений вершин и для кластеризации вершин графа.

Математическая интуиция за формулами

Попробуем пояснить подробнее, откуда берётся такая формула для обновления .

Пусть — некоторый скалярный «сигнал» на графе, который мы запишем в виде вектора (длина которого равна числу вершин графа).

Мы будем работать не с обычным Лапласианом, а с нормализованным, равным . Нормализованный лапласиан — симметричная матрица, так что у него есть ортонормированный базис из собственных векторов. Запишем базис в (ортогональную) матрицу . Тогда произведение — это вектор, состоящий из координат сигнала в базисе . Казалось бы, мы делаем тривиальные вещи из линейной алгебры, но на самом деле мы занимается анализом Фурье, а именно:

• — гармоники;
• — коэффициенты Фурье;
• умножение на — преобразование Фурье;
• умножение на — обратное преобразование Фурье.

Действительно, преобразование Фурье — это, грубо говоря, всего лишь разложение по какому-то удобному ортонормированному базису. В данном случае — по базису .

В мире функций, функциональных свёрток и обычного преобразования Фурье свёртка удовлетворяет такому соотношению:

где — поэлементное умножение. То есть при переходе в мир коэффициентов Фурье свёртка функций превращается в поэлементное умножение векторов.

Для графов кажется логичным свёртку двух сигналов и определить похожим образом:

где через мы обозначили диагональную матрицу с диагональю .

Итак, мы дали новое определение свёртки на графе — через лапласиан и его собственные векторы. Проблема в том, что вычислять очень долго. Поэтому мы линеаризуем задачу. Рассмотрим свёртку как функцию от нормализованного лапласиана и разложим её в ряд Тейлора в точке (единичная матрица):

Теперь для простоты ещё больше огрубим модель и предположим, что (обозначим это число буквой ). Тогда остаётся

А для улучшения численной устойчивости мы перепишем это так:

Получилась та самая формула, которую вы видели выше.

Более подробно о том, как устроен анализ Фурье на графах, вы можете прочитать, например, в этой статье. Кроме того, рекомендуем заглянуть в оригинальную статью про GCN за более подробным изложением вывода формул.