Задача кластеризации
В задаче классификации мы имели дело с восстановлением отображения из множества объектов в конечный набор меток классов. При этом классы были зафиксированы заранее, то есть мы с самого начала примерно понимали, какого рода объекты должны относиться к каждому из них, и мы располагали обучающей выборкой с примерами объектов и классов, к которым они относятся. В задаче кластеризации мы тоже разбиваем объекты на конечное множество классов, но у нас нет ни обучающей выборки, ни понимания, какой будет природа этих классов. То, что модель кластеризации какие-то объекты сочла «похожими», отнеся к одному классу, будет новой информацией, «открытием», сделанным этой моделью. Обучающей выборки у нас также не будет: ведь мы не знаем заранее, что за классы получатся (а иногда и сколько их будет). Таким образом, кластеризация — это задача обучения без учителя. Из-за общего сходства постановок задач в литературе кластеризацию иногда называют unsupervised classification.
Методы кластеризации часто применяют, когда фактически нужно решить задачу классификации, но обучающую выборку собрать затруднительно (дорого или долго). При этом валидационную выборку для оценки результатов кластеризации собрать значительно проще, так как для неё требуется меньше примеров. При этом стоит помнить, что точность работы supervised-методов значительно выше. Поэтому, если обучающую выборку всё-таки можно собрать, лучше решать задачу классификации, чем задачу кластеризации.
Примеры задач кластеризации
Хороший пример применения методов кластеризации — анализ геоданных. В мобильных приложениях, собирающих геоданные пользователей, часто требуется понять, где именно пользователь находился. GPS-координаты известны с некоторой погрешностью, пользователь тоже обычно двигается, поэтому вместо точного положения часто приходится иметь дело с роем точек. Положение усугубляется, когда мы пытаемся анализировать поведение сразу тысяч людей в какой-то локации — например, определить, в каких точках люди чаще всего садятся в такси у аэропорта. Может показаться, что достаточно посмотреть на данные — и мы увидим в точности нужные нам кластеры. Изображение ниже показывает, как может выглядеть ситуация всего для нескольких пользователей: согласно данным GPS, такси подбирают пассажиров и внутри здания аэропорта, и на взлётной полосе, и там, где это происходит на самом деле:
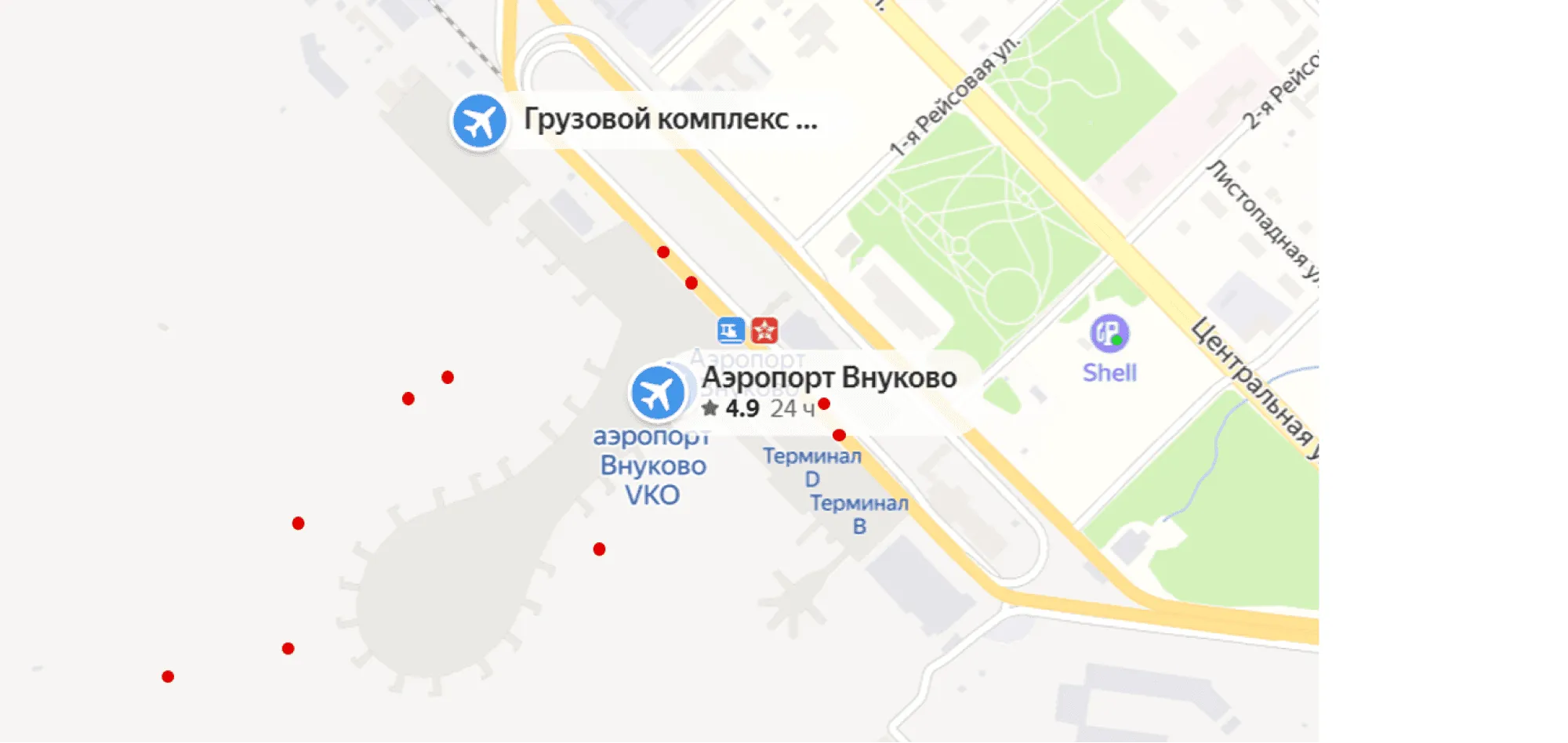
Подобная задача решалась в Яндекс.Такси при разработке пикап-пойнтов (наиболее удобных точек вызова такси, подсвечиваемых в приложении). Координаты точек заказа кластеризовались таким образом, чтобы кластер соответствовал какому-то одному, удобному для пользователя месту, и центры кластеров использовались как кандидаты в пикап-пойнты. Те кандидаты, которые удовлетворяли простым фильтрам (например, не попадали в здание или в воду), использовались в приложении. При этом не обходилось и без вручную проставленных пикап-пойнтов: например, такое решение использовалось в окрестностях аэропортов.
Другой пример кластеризации геоданных, который всегда рядом с нами, — это интерфейсы для просмотра фотографий в вашем смартфоне. Почти наверняка вы можете просмотреть их в привязке к местам, где они были сделаны, и по мере масштабирования карты вы будете видеть разное количество кластеров фотографий. Кстати, если говорить об интерфейсах, то есть и другой интересный пример: если нужно подстроить цветовую схему вашего интерфейса под выбираемое пользователем изображение (например, фоновую картинку), достаточно кластеризовать цвета из пользовательского изображения, используя RGB-представление (или любое другое) как признаки цвета, и воспользоваться для оформления цветами, соответствующими центрам кластеров.
Простейшие методы кластеризации с помощью графов
Можно приводить примеры не только про геоаналитику, однако тема геоданных поможет нам придумать пару наиболее простых и наглядных методов кластеризации. Представим, что перед нами рой геокоординат и нам нужно предложить по этим данным пикап-пойнты для такси. Разберём пару очевидных методов.
Выделение компонент связности
Логично попробовать объединить точки, которые находятся друг от друга на расстоянии двух-трёх метров, а потом просто выбрать наиболее популярные места. Для этого давайте построим на известных нам точках граф: точки, расстояние между которыми в пределах трёх метров, мы соединим рёбрами. Выделим в этом графе компоненты связности, они и будут нашими кластерами.
У этого способа есть пара очевидных недостатков. Во-первых, может найтись сколько угодно длинная цепочка точек, в которой соседние отстоят друг от друга на пару метров, — и вся она попадёт в одну компоненту связности. В итоге наша отсечка по трём метрам имеет очень опосредованное отношение к диаметру кластеров, а сами кластеры будут получаться значительно больше, чем нам хотелось бы. Во-вторых (и с первой проблемой это тоже связано), непонятно, как мы выбираем максимальное расстояние, при котором соединяем точки ребром. В данной задаче ещё можно предъявить хоть какую-то логику, а вот если бы мы кластеризовали не геометки, а что-то многомерное, например электронные письма по их тематике, придумать отсечку было бы уже сложнее. Если наша цель — не только решить практическую задачу, но и придумать достаточно общий метод кластеризации, понятно, что нам хочется понимать, как подбирать параметры этого метода (в данном случае условие добавления рёбер в граф). Эти соображения могут привести нас к другому решению.
Минимальное остовное дерево
Вместо того чтобы проводить рёбра в графе, давайте их удалять. Построим минимальное остовное дерево, считая расстояния между точками весами рёбер. Тогда, удалив рёбер с наибольшим весом, мы получим компоненту связности, которые, как и в прошлом подходе, будем считать кластерами. Различие в том, что теперь нам нужно задавать не расстояние, при котором проводится ребро, а количество кластеров. С одной стороны, если мы решаем задачу расчёта пикап-пойнтов в какой-то конкретной локации (аэропорт, торговый центр, жилой дом), нам может быть понятно, сколько примерно пикап-пойнтов мы хотим получить. С другой стороны, даже без локального рассмотрения можно просто сделать достаточно много кластеров, чтобы было из чего выбирать, но при этом достаточно мало, чтобы в каждый кластер попадало репрезентативное количество точек. Аналогичная логика будет справедлива и во многих других задачах кластеризации: количество кластеров — достаточно общий и достаточно хорошо интерпретируемый параметр, чтобы настраивать его вручную, поэтому во многих методах кластеризации количество кластеров выступает как гиперпараметр.
Далее будем рассматривать некоторую обобщённую задачу кластеризации без привязки к нашему примеру с анализом геоданных. Мы приведём три наиболее популярных метода кластеризации — k-средних, иерархическую кластеризацию и DBSCAN, а затем рассмотрим вопросы оценки качества кластеризации.
Метод K средних
Пожалуй, один из наиболее популярных методов кластеризации — это метод K-средних (K-means). Основная идея метода — итеративное повторение двух шагов:
- распределение объектов выборки по кластерам;
- пересчёт центров кластеров.
В начале работы алгоритма выбираются случайных центров в пространстве признаков. Каждый объект выборки относят к тому кластеру, к центру которого объект оказался ближе. Далее центры кластеров пересчитывают как среднее арифметическое векторов признаков всех вошедших в этот кластер объектов (то есть центр масс кластера). Как только мы обновили центры кластеров, объекты заново перераспределяются по ним, а затем можно снова уточнить положение центров. Процесс продолжается до тех пор, пока центры кластеров не перестанут меняться.
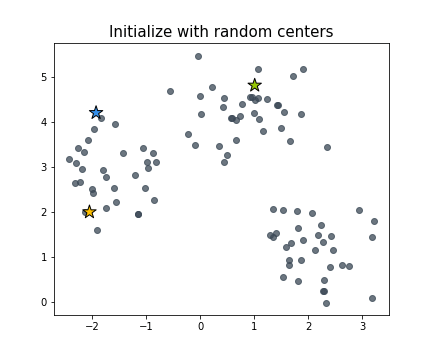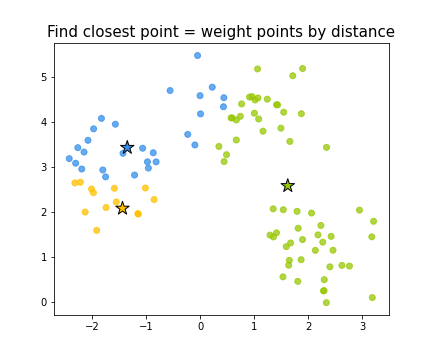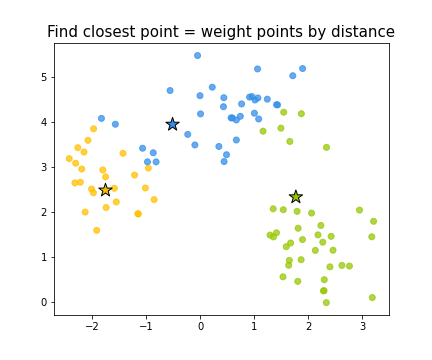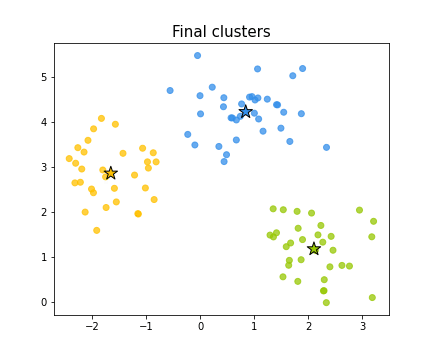
Выбор начального приближения
Первый вопрос при выборе начального положения центров — как, выбирая центры из некоторого случайного распределения, не попасть в область пространства признаков, где нет точек выборки. Базовое решение — просто выбрать в качестве центров какие-то из объектов выборки.
Вторая потенциальная проблема — кучное размещение центров. В этом случае их начальное положение с большой вероятностью окажется далёким от итогового положения центров кластеров. Например, для таких изначальных положений центров
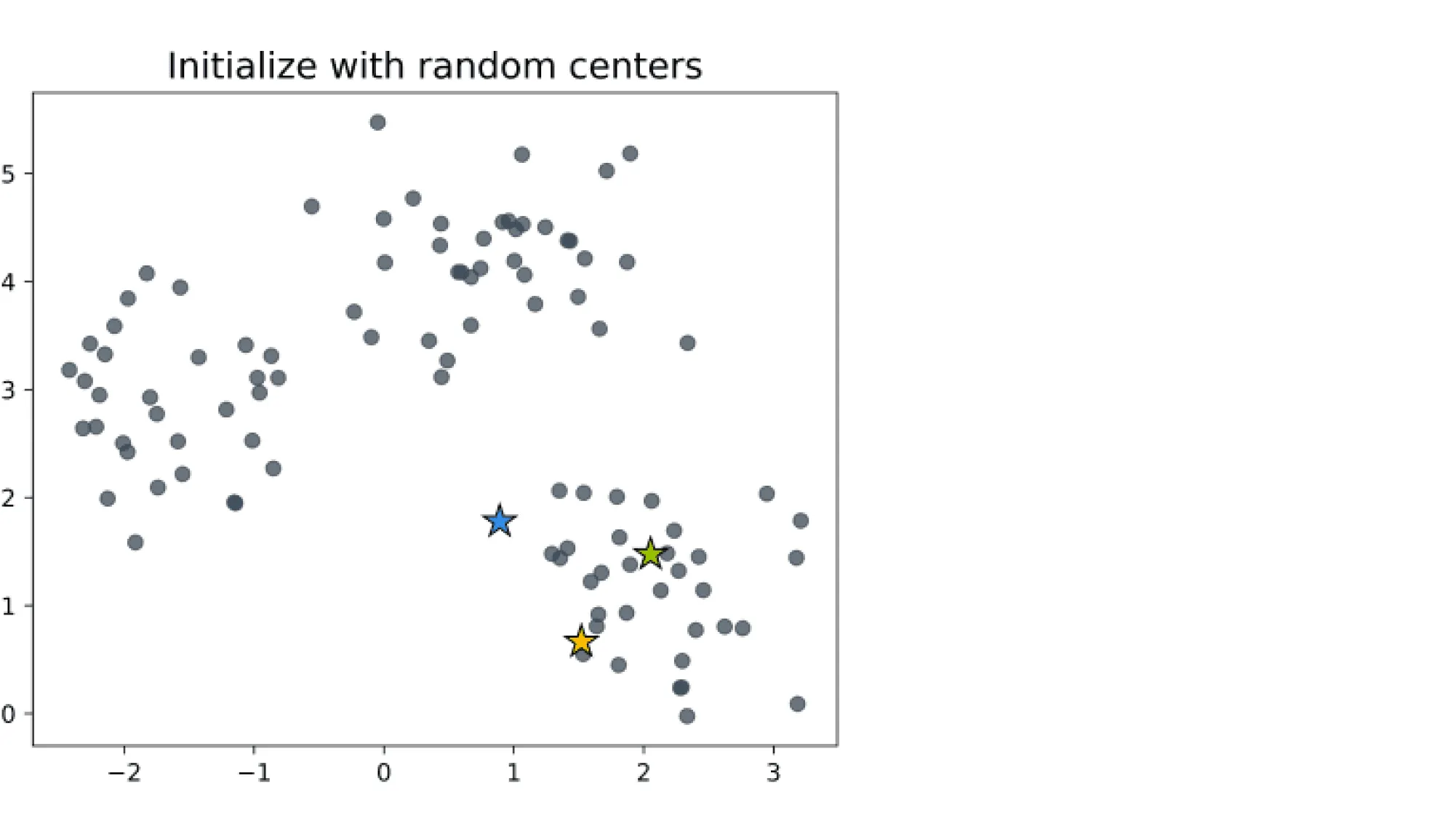
мы получим неправильную кластеризацию.
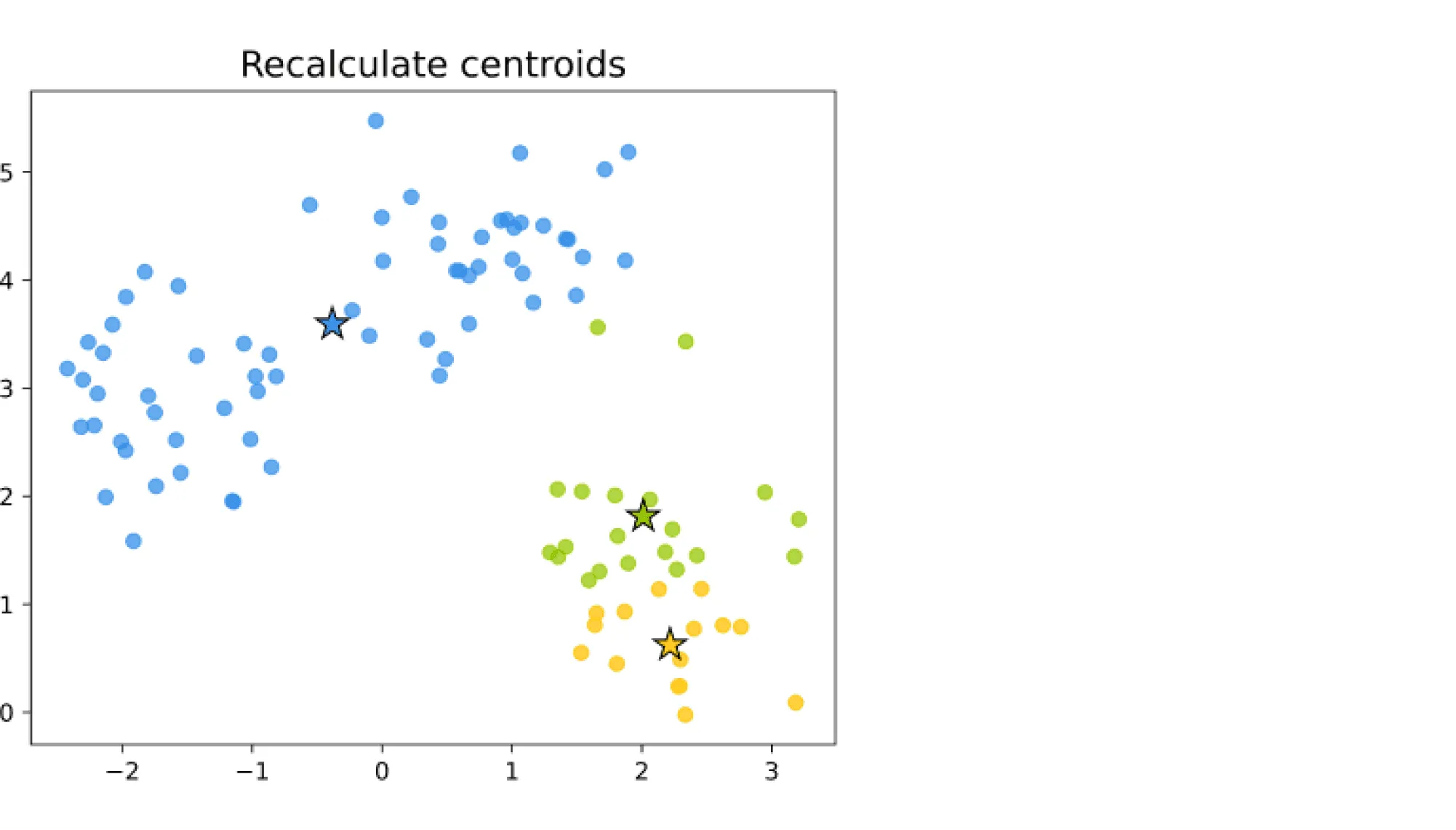
Чтобы бороться с этим явлением, выгодно брать максимально удаленные друг от друга центры.
На практике работает следующая эвристика:
- первый центр выбираем случайно из равномерного распределения на точках выборки;
- каждый следующий центр выбираем из случайного распределения на объектах выборки, в котором вероятность выбрать объект пропорциональна квадрату расстояния от него до ближайшего к нему центра кластера.
Модификация K-means, использующая эту эвристику для выбора начальных приближений, называется K-means++.
Выбор метрик
Так как работа метода K-средних состоит из последовательного повторения до сходимости двух шагов, обоснованность применения различных метрик (расстояний между точками, а не метрик качества 😃 или функций близости связана с тем, «ломают» они какой-либо из этих шагов или нет.
Первый шаг с отнесением объектов к ближайшим центрам не зависит от вида метрики. Второй шаг предполагает пересчёт центров как среднего арифметического входящих в кластер точек, и вот здесь будет подвох: к оптимальности выбора центров в среднем арифметическом приводит именно евклидова метрика (подробнее в разделе «Что оптимизирует K-means»).
Однако на практике никто не мешает использовать метод и без должного обоснования, поэтому можно экспериментировать с любыми расстояниями, с той лишь оговоркой, что не будет никаких теоретических гарантий, что метод сработает. Наиболее распространённая альтернатива евклидовой метрике — это косинусная мера близости векторов (она особенно популярна в задачах анализа текстов):
При её использовании стоит не забывать, что косинусная мера — это функция близости, а не расстояние, так что чем больше её значения, тем ближе друг к другу векторы.
Mini-batch K-means
Несложно заметить, что, если считать и размерность пространства признаков константами, оба шага алгоритма работают за , где n — количество объектов обучающей выборки. Отсюда возникает идея ускорения работы алгоритма. В mini-batch K-means мы не считаем шаги сразу на всей выборке, а на каждой итерации выбираем случайную подвыборку (мини-батч) и работаем на ней. В случае когда исходная выборка очень велика, переход к пакетной обработке не приводит к большой потере качества, зато значительно ускоряет работу алгоритма.
Понижение размерности
С другой стороны, вычисление расстояний и средних делается за , где — размерность пространства признаков, так что другая идея ускорения K-means — это предварительно понизить размерность пространства признаков (с помощью PCA или эмбеддингов). Особенно удачно эта идея работает в задачах кластеризации текстов, когда K-means применяют на эмбеддингах слов: получается выиграть не только в скорости работы, но и в интерпретируемости результатов кластеризации.
Кстати, сам алгоритм кластеризации тоже можно использовать как метод понижения размерности. Если вы решаете задачу обучения с учителем и пространство признаков очень разнообразно (то есть обучающая выборка не даёт вам достаточно статистики при столь большом числе признаков), можно выполнить кластеризацию объектов выборки на 500 или 1000 кластеров и оперировать попаданием объектов в какой-то кластер как признаком. Такой подход называется квантизацией пространства признаков (feature space quantization) и часто помогает на практике, когда нужно огрубить признаки, добавить им интерпретируемости или же, наоборот, обезличить.
Хрестоматийный пример такого использования кластеризации — метод bag of visual words, расширяющий bag of words из анализа текстов на работу с изображениями. Идея метода в том, чтобы строить признаковое описание изображений на основе входящих в него фрагментов: так, изображения с лицами будут содержать фрагменты с носом, глазами, ртом, а изображения с машинами — колёса, зеркала, двери. Но проблема здесь в том, что нарезать такие фрагменты из обучающей выборки и искать точные совпадения в новых примерах изображений, которые нужно классифицировать, — безнадёжная затея. В жизни фрагменты изображений не повторяются в других изображениях с попиксельной точностью. Решение этой проблемы оказалось возможным при помощи алгоритмов кластеризации (исторически использовался именно K-means): фрагменты изображений из обучающей выборки кластеризовали на 100–1000 кластеров («визуальных слов»), а проходясь по новым изображениям, также нарезали их на фрагменты и относили к одному из этих кластеров. В итоге как новые изображения, так и изображения из обучающей выборки можно было описать количеством вхождений в них фрагментов из различных кластеров («визуальных слов»), так же как в анализе текстов описывают текст количеством вхождений в него слов из словаря. В таком признаковом пространстве уже можно было успешно обучать модели машинного обучения.
Сейчас выделение «визуальных слов» в задаче классификации изображений происходит автоматически: с одной стороны, задачи компьютерного зрения теперь решаются нейросетями, но с другой стороны — если мы визуализируем отдельные слои этих нейросетей, станет понятно, что их логика работы во многом похожа на описанную выше. При этом идея квантизации признаков не утратила своей актуальности. Вот лишь несколько современных примеров её применения:
- Если вам необходимо дать возможность заказчику (например, внешней компании) анализировать используемые вами признаки — отсутствие провалов в данных и какие-то другие общие показатели, но нельзя отдавать признаки как есть (например, из-за законодательства, регулирующего передачу пользовательских данных), возможное решение — это агрегировать признаки по кластерам.
- Та же цель может быть отчасти достигнута, если перейти к самим кластерам как к признакам, чтобы скрыть исходные признаки.
- Переход к кластерам может быть сделан не с целью что-то скрыть, а наоборот, с целью повысить интерпретируемость: исходные сырые данные часто не вполне понятны бизнесу, но позволяют построить маркетинговые сегменты по различным коммерческим интересам пользователей, из-за чего становится удобно показывать принадлежность к этим сегментам как исходные признаки, не вдаваясь в детали о том, на каких данных эти сегменты построены.
- Для ускорения поиска похожих объектов в пространстве признаков вы также можете проводить поиск внутри того же кластера и соседних кластеров, так что за счёт «огрублённого» вида признаков какие-то процессы можно ещё и ускорить.
Что оптимизирует K-means
Проговорим на интуитивном уровне, какую оптимизационную задачу решает K-means.
Оба шага алгоритма работают на уменьшение среднего квадрата евклидова расстояния от объектов до центров их кластеров:
На шаге отнесения объектов к одному из кластеров мы выбираем кластер с ближайшим центроидом, то есть минимизируем каждое слагаемое в : все потенциально большие слагаемые мы зануляем, а оставляем ненулевыми только наименьшие из возможных (при условии фиксирования центров кластеров).
На шаге пересчёта центров кластеров мы выбираем центр таким образом, чтобы при фиксированном наборе объектов, относящихся к кластеру, для всех минимизировать выражение, стоящее под суммой по :
Здесь уже становится принципиально, что мы определяем квадрат расстояния как квадрат разности векторов, так как именно отсюда при дифференцировании по и записи необходимого условия экстремума получается, что центры кластеров нужно пересчитывать как средние арифметические , принадлежащих кластеру.
Этих соображений, конечно, недостаточно, чтобы утверждать, что мы найдём минимум . Более того, гарантии того, что мы найдём глобальный минимум, вообще говоря, нет. Однако, потратив чуть больше усилий, можно доказать, что процесс сойдётся в один из локальных минимумов.
Также можно справедливо заметить, что, так как любой центр кластера — это среднее арифметическое входящих в кластер объектов , на выборке фиксированного размера есть лишь конечное множество потенциальных центров кластеров. Если предположить, что в ходе работы K-means не зацикливается, отсюда следует, что рано или поздно центры кластеров не изменятся на следующем шаге и алгоритм сойдётся. При этом фактическая сходимость, конечно же, происходит задолго до полного перебора всех возможных центров кластеров.
Иерархическая агломеративная кластеризация
Другой классический метод кластеризации — это иерархическая кластеризация. Иногда дополнительно уточняют: иерархическая агломеративная кластеризация. Название указывает сразу на два обстоятельства.
Во-первых, есть деление алгоритмов кластеризации на агломеративные (agglomerative) и дивизивные, или дивизионные (divisive). Агломеративные алгоритмы начинают с небольших кластеров (обычно с кластеров, состоящих из одного объекта) и постепенно объединяют их в кластеры побольше. Дивизивные начинают с больших кластеров (обычно – с одного единственного кластера) и постепенно делят на кластеры поменьше.
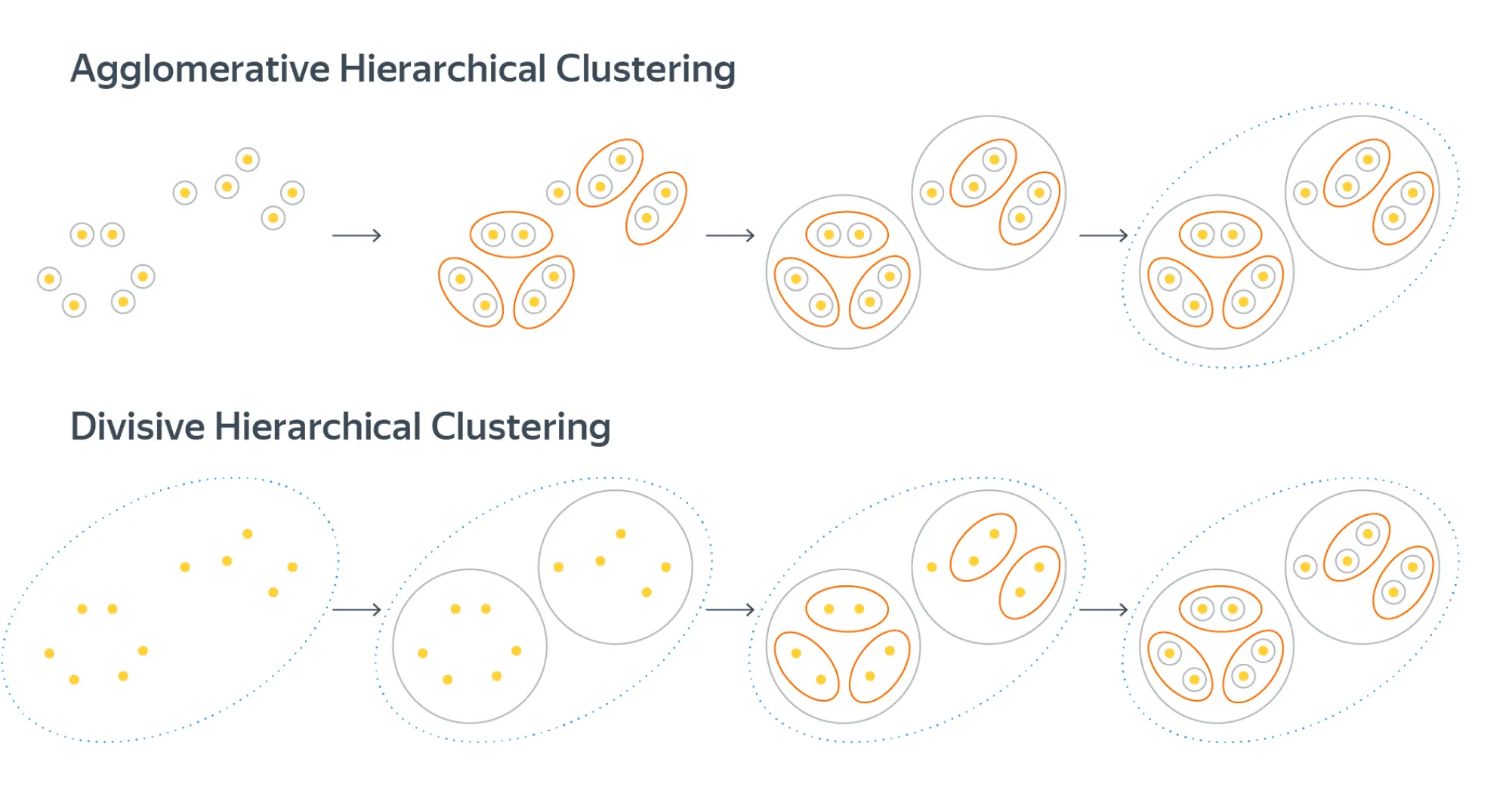
Во-вторых, кластеризация бывает, по аналогии с оргструктурой в организациях, плоской (когда все кластеры равноправны и находятся на одном уровне кластеризации) и иерархической (когда кластеры бывают вложены друг в друга и образуют древовидную структуру).
В случае иерархической агломеративной кластеризации мы действительно будем начинать с кластеров из одного объекта, постепенно объединяя их, а уже последовательность этих объединений даст структуру вложенности кластеров. Даже если в итоге мы будем использовать кластеры с одного уровня, не углубляясь ни в какую вложенность, кластеризация всё равно называется иерархической, так как иерархия естественным образом возникает в процессе работы алгоритма.
Сам алгоритм выглядит предельно просто:
- Создаём столько кластеров, сколько у нас объектов в выборке, каждый объект — в своём отдельном кластере.
- Повторяем итеративно слияние двух ближайших кластеров, пока не выполнится критерий останова.
Расстояния в иерархической кластеризации
Как измерить расстояние между кластерами из одного объекта? Нужно просто взять расстояние между этими объектами. Остаётся вопрос, как обобщить расстояние между объектами до расстояния между кластерами (если в них более одного объекта). Традиционные решения — брать среднее расстояние между объектами кластеров, минимальное расстояние или максимальное. Если обозначить кластеры и , расстояние между ними в этом случае можем вычислять по одной из формул:
Используемая формула расстояния между кластерами — один из гиперпараметров алгоритма. Кроме приведённых стандартных вариантов бывают и более экзотичные, например расстояние Уорда (Ward distance). В наиболее общем виде способы задания расстояния между кластерами даются формулой Ланса — Уильямса (Lance — Williams; более подробно вы можете почитать в этой статье). Сами же расстояния между объектами можно задавать любой метрикой, как евклидовой, так и манхэттенским расстоянием или, например, косинусной мерой (с той лишь поправкой, что это мера близости, а не расстояние).
Условия окончания работы алгоритма (критерии останова)
В качестве условия для завершения работы алгоритма можем выбрать либо получение нужного количества кластеров (количество кластеров может быть гиперпараметром алгоритма), либо выполнение эвристик на основе расстояния между объединяемыми кластерами (например, если расстояние сливаемых кластеров значительно выросло по сравнению с прошлой итерацией). На практике же обычно кластеризацию проводят вплоть до одного кластера, включающего в себя всю выборку, а затем анализируют получившуюся иерархическую структуру с помощью дендрограммы.
Дендрограмма
По мере объединения кластеров, каждой итерации алгоритма соответствует пара объединяемых на этой итерации кластеров, а также расстояние между кластерами в момент слияния. Расстояния с ростом итерации будут только увеличиваться, поэтому возникает возможность построить следующую схему, называемую дендрограммой:
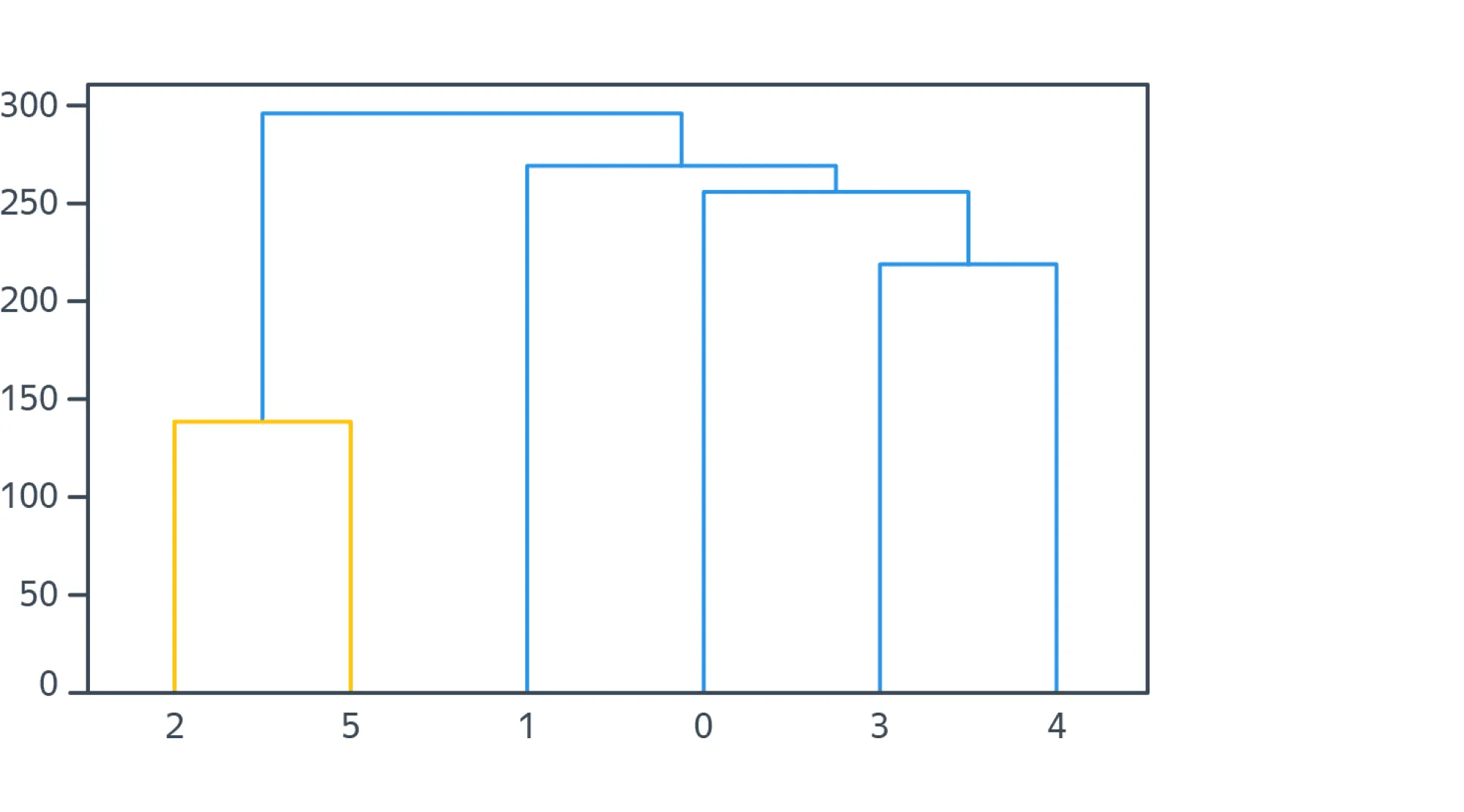
Здесь по горизонтали внизу отмечены объекты кластеризуемой выборки, под горизонтальной осью подписаны номера объектов, а их расположение вдоль оси продиктовано только эстетическими соображениями: нам удобно строить дендрограмму так, чтобы никакие дуги в ней не пересекались. По вертикали отложены расстояния между кластерами в момент слияния. Когда происходит объединение кластеров, состоящих из нескольких объектов, соответствующая этой итерации алгоритма дуга идёт не до конкретных объектов выборки, а до дуги другого кластера.
Таким образом мы получаем наглядную визуализацию древовидной структуры процесса кластеризации. В частности, на дендрограмме мы можем визуально заметить, в какой момент происходит скачок расстояний между кластерами, и попытаться определить «естественное» количество кластеров в нашей задаче. На практике же это соображение, как правило, остаётся лишь красивой теорией, так как любую кластеризацию можно делать в разной степени «мелкой» и «естественного» количества кластеров в практических задачах часто не существует. В случае же если данные были получены таким образом, что в них действительно есть какое-то естественное количество кластеров, иерархическая кластеризация обычно справляется с определением числа кластеров по дендрограмме заметно хуже, чем DBSCAN. Именно алгоритму DBSCAN мы и посвятим следующий раздел.
DBSCAN
Алгоритм DBSCAN (Density-based spatial clustering of applications with noise) развивает идею кластеризации с помощью выделения связных компонент.
Прежде чем перейти к построению графа, введём понятие плотности объектов выборки в пространстве признаков. Плотность в DBSCAN определяется в окрестности каждого объекта выборки как количество других точек выборки в шаре . Кроме радиуса окрестности в качестве гиперпараметра алгоритма задается порог по количеству точек в окрестности.
Далее все объекты выборки делятся на три типа: внутренние / основные точки (core points), граничные (border points) и шумовые точки (noise points). К основным относятся точки, в окрестности которых больше объектов выборки. К граничным — точки, в окрестности которых есть основные, но общее количество точек в окрестности меньше . Шумовыми называют точки, в окрестности которых нет основных точек и в целом содержится менее объектов выборки.
Алгоритм кластеризации выглядит следующим образом:
- Шумовые точки убираются из рассмотрения и не приписываются ни к какому кластеру.
- Основные точки, у которых есть общая окрестность, соединяются ребром.
- В полученном графе выделяются компоненты связности.
- Каждая граничная точка относится к тому кластеру, в который попала ближайшая к ней основная точка.
Удобство DBSCAN заключается в том, что он сам определяет количество кластеров (по модулю задания других гиперпараметров — и ), а также в том, что метод успешно справляется даже с достаточно сложными формами кластеров. Кластеры могут иметь вид протяжённых лент или быть вложенными друг в друга как концентрические гиперсферы. На изображении ниже показан пример выделения кластеров достаточно сложной формы с помощью DBSCAN:
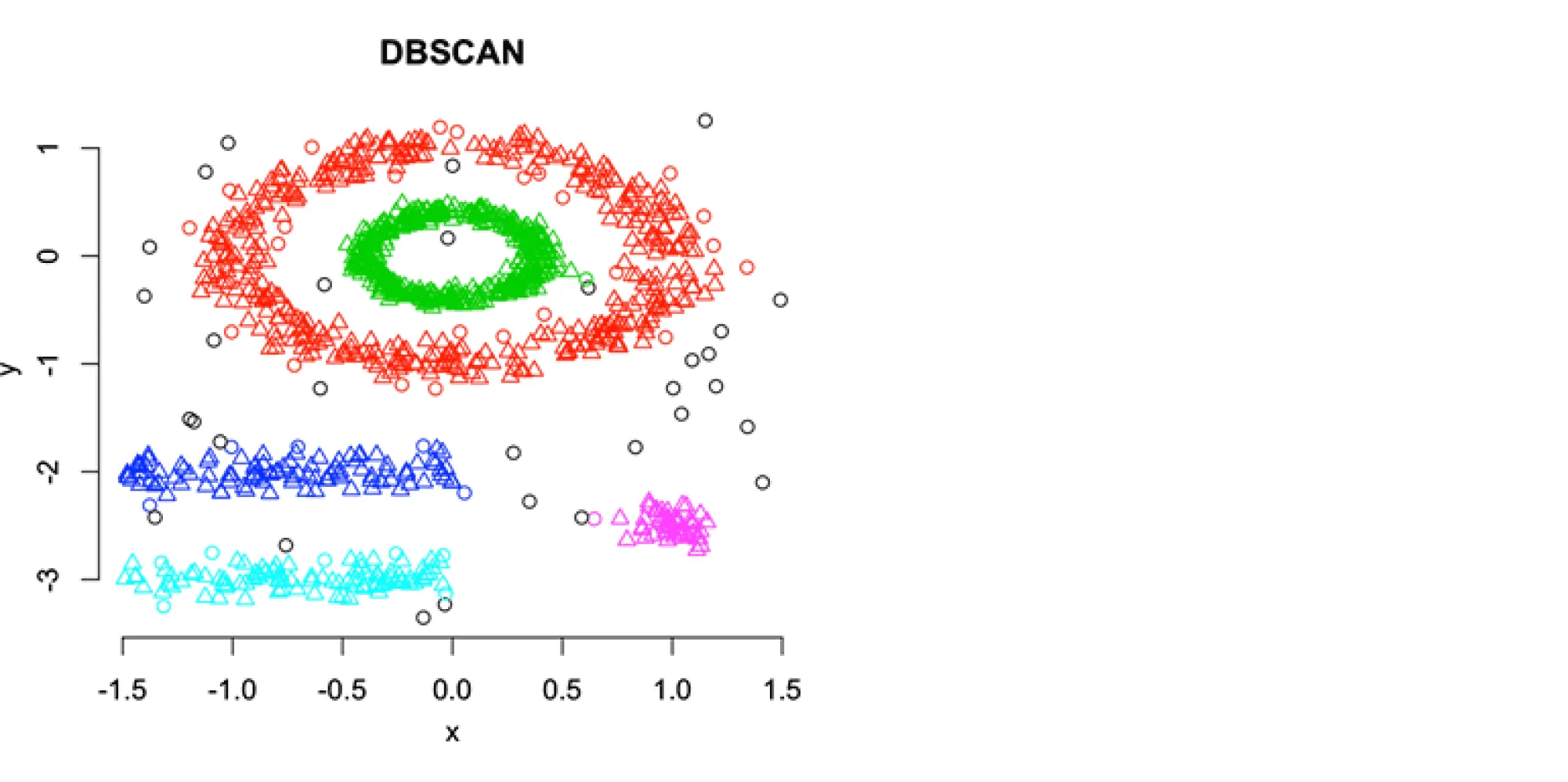
DBSCAN — один из самых сильных алгоритмов кластеризации, но работает он, как правило, заметно дольше, чем mini-batch K-means, к тому же весьма чувствителен к размерности пространства признаков, поэтому используется на практике DBSCAN только тогда, когда успевает отрабатывать за приемлемое время.
Какой метод кластеризации выбирать?
Если сравнивать частоту использования K-means, иерархической кластеризации и DBSCAN, то на первом месте, бесспорно, будет K-means, а второе место будут делить иерархический подход и DBSCAN. Иерархическая кластеризация — более известный и простой в понимании метод, чем DBSCAN, но довольно редко отрабатывающий качественно. Частая проблема иерархической кластеризации — раннее образование одного гигантского кластера и ряда очень небольших, что приводит к сильной несбалансированности количества объектов в итоговых кластерах. В то же время DBSCAN — менее широко известный подход, но, когда его можно применить, качество, как правило, получается выше, чем в K-means или иерархической кластеризации.
Оценка качества кластеризации
Далее приведём список основных метрик качества кластеризации и обсудим некоторые особенности их применения.
Среднее внутрикластерное расстояние
Смысл среднего внутрикластерного расстояния максимально соответствует названию:
Сумма расстояний между точками из одного и того же кластера делится на количество пар точек, принадлежащих к одному кластеру. В приведённой выше формуле пары вида включены в рассмотрение, чтобы избежать неопределённости в случае, когда в каждом кластере ровно по одному объекту. Однако иногда записывают суммы по , просто доопределяя в описанном случае нулём.
Решая задачу кластеризации, мы хотим по возможности получать как можно более кучные кластеры, то есть минимизировать .
В случае если у кластеров есть центры , часто рассматривается аналогичная метрика — средний квадрат внутрикластерного расстояния:
Среднее межкластерное расстояние
Аналогично среднему внутрикластерному расстоянию вводится среднее межкластерное:
Среднее межкластерное расстояние, напротив, нужно максимизировать, то есть имеет смысл выделять в разные кластеры наиболее удалённые друг от друга объекты.
Гомогенность
Для измерения следующих метрик (гомогенности, полноты и V-меры) нам уже потребуется разметка выборки. Будем обозначать кластеры, к которым наш алгоритм кластеризации относит каждый объект, буквами , а классы, к которым объекты отнесены разметкой, — буквами . Разумный вопрос при наличии разметки — зачем нам решать задачу кластеризации, если с разметкой можно поставить задачу как задачу классификации. Это и правда хороший вопрос в том случае, если размеченных данных достаточно много для обучения классификатора. На практике же часто встречаются ситуации, когда данных достаточно для оценки качества кластеризации, но всё ещё не хватает для использования методов обучения с учителем.
Пусть — общее количество объектов в выборке, — количество объектов в кластере номер , — количество объектов в классе номер , а — количество объектов из класса в кластере . Рассмотрим следующие величины:
Несложно заметить, что эти величины соответствуют формуле энтропии и условной энтропии для мультиномиальных распределений , и соответственно.
Гомогенность кластеризации определяется следующим выражением:
Отношение показывает, во сколько раз энтропия изменяется за счёт того, что мы считаем известной принадлежность объектов к выделенным нашим алгоритмом кластерам. Худший случай — когда отношение оказывается равным единице (энтропия не изменилась, условная энтропия совпала с обычной), лучший — когда каждый кластер содержит элементы только одного класса и номер кластера, таким образом, точно определяет номер класса (в этом случае ).
Тривиальный способ максимизировать гомогенность кластеризации — выделить каждый объект выборки в отдельный кластер.
Полнота
Полнота задаётся аналогично гомогенности, с той лишь разницей, что вводится величина , симметричная :
Полнота равна единице, когда все объекты класса всегда оказываются в одном кластере.
Тривиальный способ максимизировать полноту кластеризации — объединить всю выборку в один кластер.
V-мера
Гомогенность и полнота кластеризации – это в некотором смысле аналоги точности и полноты классификации. Аналог F-меры для задачи кластеризации тоже есть, он называется V-мерой и связан с гомогенностью и полнотой той же формулой, что и F-мера с точностью и полнотой:
В частности, по аналогии с -мерой в классификации (не путать со средним межкластерным расстоянием, которое мы тоже обозначали выше) будет просто средним гармоническим гомогенности и полноты:
V-мера комбинирует в себе гомогенность и полноту таким образом, чтобы максимизация итоговой метрики не приводила к тривиальным решениям.
Коэффициент силуэта
Ещё одна метрика кластеризации, на этот раз уже не требующая разметки, это коэффициент силуэта (silhouette coefficient). Изначально коэффициент определяется для каждого объекта выборки, а метрика для результатов кластеризации всей выборки вводится как средний коэффициент силуэта для всех объектов выборки.
Чтобы ввести коэффициент силуэта , нам потребуются две вспомогательные величины. Первая, , — это среднее расстояние между и объектами того же кластера. Вторая, , — это среднее расстояние между и объектами следующего ближайшего кластера. Коэффициент силуэта вводится следующим образом:
В идеальном случае объекты «родного» кластера должны быть ближе к , чем объекты соседнего кластера, то есть . Однако это неравенство выполняется далеко не всегда. Если «родной» кластер , например, имеет форму очень протяжённой ленты или просто большой размер, а недалеко от есть кластер поменьше, может оказаться, что . Таким образом, если мы посмотрим на разность , она может оказаться как положительной, так и отрицательной, но в идеальном сценарии всё же следует ожидать положительное значение. Сам же коэффициент принимает значения от –1 до +1 и максимизируется, когда кластеры кучные и хорошо отделены друг от друга.
Коэффициент силуэта особенно полезен (по сравнению с другими приведёнными метриками) тем, что одновременно и не требует разметки, и позволяет подбирать количество кластеров. См. подробнее в примере из документации scikit-learn.
Различия и выбор метрик качества кластеризации
Подводя итог в теме метрик качества в задаче кластеризации, отметим, что есть несколько разных сценариев использования этих метрик. Если вы уже определились с количеством кластеров, можно оптимизировать среднее внутрикластерное или среднее межкластерное расстояние. Если у вас ещё и есть разметка — гомогенность и полноту. V-мера за счёт сочетания гомогенности и полноты в целом позволяет выполнять и подбор количества кластеров.
Однако разметка, с одной стороны, есть далеко не всегда, а с другой стороны, в задаче кластеризации часто очень субъективна. Сложность кластеризации в том, что на одной и той же выборке нас вполне могут устроить сразу несколько различных вариантов кластеризации, то есть задача поставлена некорректно и имеет более одного решения. Формализовать, какие решения нас устроят, на практике довольно сложно, поэтому сама по себе задача кластеризации решается не слишком хорошо.
Если разметки нет и число кластеров не фиксировано, лучшая метрика на практике — коэффициент силуэта. Исключение — ситуация, когда результат кластеризации используется далее для решения некоторой задачи обучения с учителем (как было в примере классификации изображений с помощью visual bag of words). В этом случае можно абстрагироваться от качества кластеризации и выбирать такой алгоритм кластеризации и такие его гиперпараметры, которые позволят лучше всего решить итоговую задачу.