Введение

В предыдущих разделах мы научились соединять базовые алгоритмы в ансамбль с помощью бэггинга (и, в частности, строить из решающих деревьев случайные леса). В ходе обучения случайного леса каждый базовый алгоритм строится независимо от остальных.

Бустинг, в свою очередь, воплощает идею последовательного построения линейной комбинации алгоритмов. Каждый следующий алгоритм старается уменьшить ошибку текущего ансамбля. Если для обучения каждого последующего базового алгоритма используется градиент ошибки ансамбля, такой бустинг называется градиентным. В этом параграфе мы рассмотрим градиентный бустинг над решающими деревьями (англ. Gradient Boosting on Decision Trees; GBDT).

Он отлично работает на выборках с «табличными», неоднородными данными. Пример таких данных — описание пользователя Яндекса через его возраст, пол, среднее число поисковых запросов в день, число заказов такси и так далее. Такой бустинг способен эффективно находить нелинейные зависимости в данных различной природы.

Этим свойством обладают все алгоритмы, которые используют деревья решений, однако именно GBDT обычно выигрывает в подавляющем большинстве задач. Благодаря этому он широко применяется во многих конкурсах по машинному обучению и задачах из индустрии:

• поисковом ранжировании;

• рекомендательных системах;

• таргетировании рекламы;

• предсказании погоды;

• выборе пункта назначения такси и многих других.

Не так хорошо бустинг проявляет себя на однородных данных: текстах, изображениях, звуке, видео. В таких задачах нейросетевые подходы почти всегда демонстрируют лучшее качество.

И хотя деревья решений — традиционный выбор для объединения в ансамбли, никто не запрещает использовать и другие алгоритмы (например, линейные модели) в качестве базовых. Эта возможность реализована в библиотеке XGBoost.

Стоит только понимать, что построенная композиция окажется линейной комбинацией линейных моделей, то есть опять-таки линейной моделью — или нейросетью с одним полносвязным слоем. Это уменьшает возможности ансамбля эффективно определять нелинейные зависимости в данных. И в этом параграфе мы рассмотрим только бустинг над решающими деревьями.

Интуиция

Рассмотрим задачу регрессии с квадратичной функцией потерь:

Для решения будем строить композицию из базовых алгоритмов:

Если мы обучим единственное решающее дерево, то качество такой модели, скорее всего, будет низким. Однако мы знаем, на каких объектах построенное дерево давало точные предсказания, а на каких ошибалось.

Попробуем использовать эту информацию и обучим ещё одну модель. Допустим, предсказание первой модели на объекте на 10 больше, чем необходимо (то есть . Если бы мы могли обучить новую модель, которая на будет выдавать ответ , то сумма ответов этих двух моделей на объекте в точности совпала бы с истинным значением:

Другими словами, если вторая модель научится предсказывать разницу между реальным значением и ответом первой, то это позволит уменьшить ошибку композиции.

В реальности вторая модель тоже не сможет обучиться идеально, поэтому обучим третью, которая будет «компенсировать» неточности первых двух. Будем продолжать так, пока не построим композицию из алгоритмов.

Для объяснения метода градиентного бустинга полезно воспользоваться следующей аналогией. Бустинг можно представить как гольфиста, цель которого — загнать мяч в лунку с координатой . Здесь положение мяча — ответ композиции . Гольфист мог бы один раз ударить по мячу, не попасть в лунку и пойти домой, но упорство заставляет его продолжить.

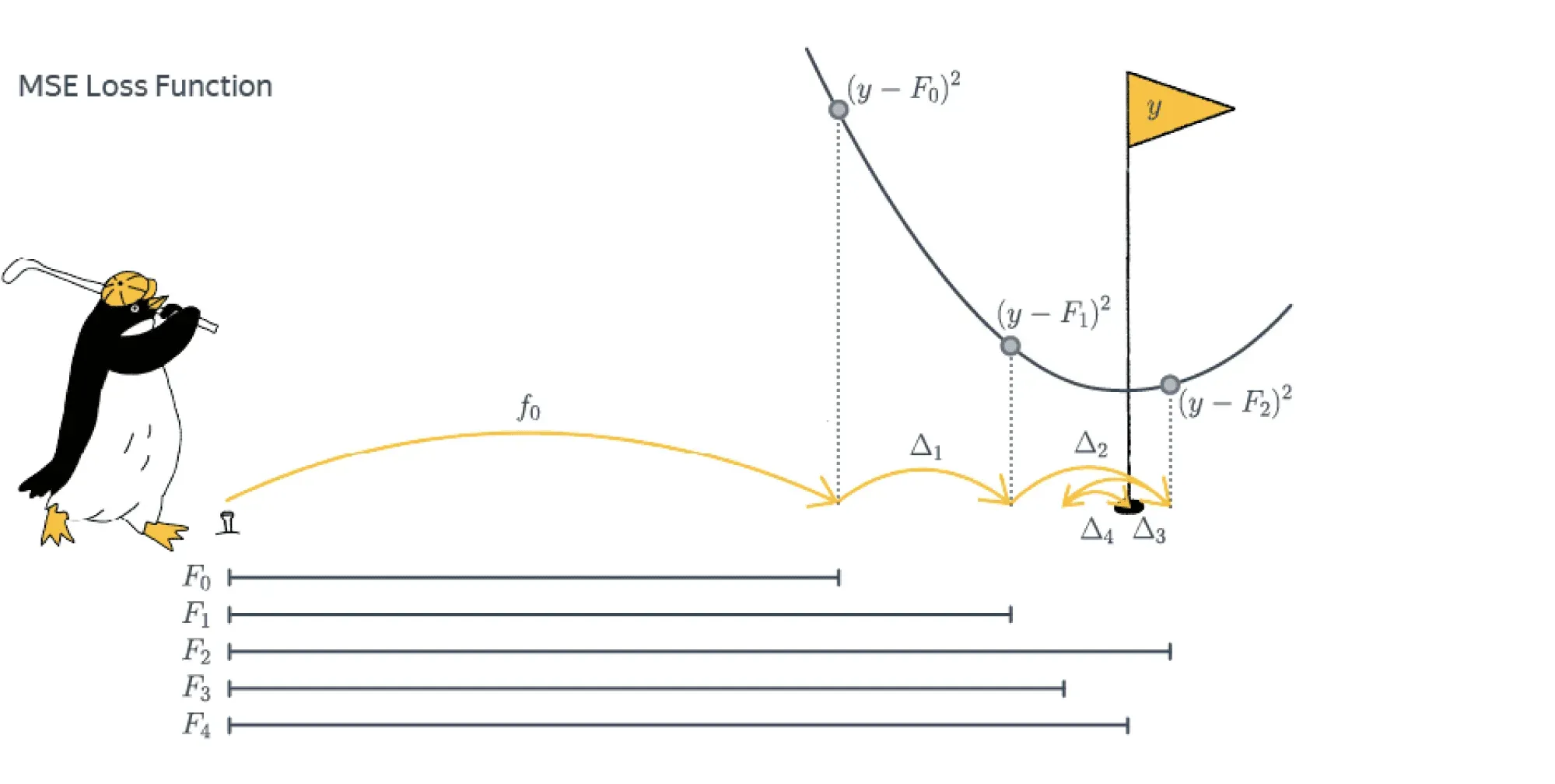
По счастью, ему не нужно стартовать каждый раз с начальной позиции. Следующий удар гольфиста переводит мяч из текущего положения в положение . Каждый следующий удар — это та поправка, которую вносит очередной базовый алгоритм в композицию. Если гольфист всё делает правильно, то функция потерь будет уменьшаться:

то есть мяч постепенно будет приближаться к лунке.

Удары при этом делаются не хаотично. Гольфист оценивает текущее положение мяча относительно лунки и следующим ударом старается нивелировать те проблемы, которые он создал себе всеми предыдущими. Подбираясь к лунке, он будет бить всё аккуратнее и, возможно, даже возьмёт другую клюшку, но точно не будет лупить так же, как из первоначальной позиции. В итоге комбинация всех ударов рано или поздно перенесёт мяч в лунку.

Подобно тому как гольфист постепенно подводит мяч к цели, бустинг с каждым новым базовым алгоритмом всё больше приближает предсказание к истинному значению метки объекта.

Рассмотрим теперь другую аналогию — разложение функции в ряд Тейлора. Из курса математического анализа известно, что (достаточно хорошую) бесконечно дифференцируемую функцию на интервале можно представить в виде бесконечной суммы степенных функций:

Одна, самая первая степенная функция в разложении очень грубо приближает . Прибавляя к ней следующую, мы получим более точное приближение. Каждая следующая элементарная функция увеличивает точность приближения, но менее заметна в общей сумме. Если нам не требуется абсолютно точное разложение, вместо бесконечного ряда Тейлора мы можем ограничиться суммой его первых элементов. Таким образом, интересующую нас функцию мы с некоторой точностью представили в виде суммы «простых» функций.

Перенесём эту идею на задачи машинного обучения. В машинном обучении мы пытаемся по выборке восстановить неизвестную истинную зависимость. Прежде всего мы выбираем подходящий алгоритм.

Мы можем выбрать «сложный» алгоритм, который сразу хорошо выучит истинную зависимость.

А можем обучить «простой», который выучит истинную зависимость посредственно. Затем мы добавим к нему ещё один такой простой алгоритм, чтобы уточнить предсказание первого алгоритма. Продолжая этот процесс, мы получим сумму простых алгоритмов, где первый алгоритм грубо приближает истинную зависимость, а каждый следующий делает приближение всё точнее.

Пример с задачей регрессии: формальное описание

Рассмотрим тот же пример с задачей регрессии и квадратичной функцией потерь:

Для решения также будем строить композицию из базовых алгоритмов семейства :

В качестве базовых алгоритмов выберем, как и условились в начале параграфа, семейство решающих деревьев некоторой фиксированной глубины.

Используя известные нам методы построения решающих деревьев, обучим алгоритм , который наилучшим образом приближает целевую переменную:

Построенный алгоритм , скорее всего, работает не идеально. Более того, если базовый алгоритм работает слишком хорошо на обучающей выборке, то высока вероятность переобучения: низкий уровень смещения, но высокий уровень разброса. Далее вычислим, насколько сильно отличаются предсказания этого дерева от истинных значений:

Теперь мы хотим скорректировать с помощью . В идеале так, чтобы безупречно предсказывал величины , ведь в этом случае

Найти совершенный алгоритм, скорее всего, не получится, но по крайней мере мы можем выбрать из семейства наилучшего представителя для такой задачи. Итак, второе решающее дерево будет обучаться предсказывать разности :

Ожидается, что композиция из двух таких моделей — — станет более качественно предсказывать целевую переменную .

Далее рассуждения повторяются до построения всей композиции. На -м шаге вычисляется разность между правильным ответом и текущим предсказанием композиции из алгоритмов:

Затем -й алгоритм учится предсказывать эту разность:

а композиция в целом обновляется по формуле

Обучение базовых алгоритмов завершает построение композиции.

Обобщение на другие функции потерь

Отметим теперь важное свойство функции потерь в рассмотренном выше примере с регрессией. Для этого посчитаем производную функции потерь по предсказанию модели для -го объекта:

Видим, что разность, на которую обучается -й алгоритм, выражается через производную:

Таким образом, для каждого объекта очередной алгоритм в бустинге обучается предсказывать антиградиент функции потерь по предсказанию модели в точке предсказания текущей части композиции на объекте .

Почему же это важно? Дело в том, что это наблюдение позволяет обобщить подход построения бустинга на произвольную дифференцируемую функцию потерь. Для этого мы заменяем обучение на разность обучением на антиградиент функции потерь , где

Вспомните аналогию с гольфистом: обучение композиции можно представить как перемещение предсказания из точки в точку . В конечном итоге мы ожидаем, что точка будет располагаться как можно ближе к точке с истинными значениями .

В случае квадратичной функции потерь интуиция вполне подкрепляется математикой. Изменится ли что-то в наших действиях, если мы поменяем квадратичную функцию потерь на любую другую?

С одной стороны, мы, как и прежде, можем двигаться в направлении уменьшения разности предсказания и истинного значения: любая функция потерь поощряет такие шаги для каждого отдельного объекта, ведь для любой адекватной функции потерь выполнено .

Но мы можем посмотреть на задачу и с другой стороны: не с точки зрения уменьшения расстояния между вектором предсказаний и вектором истинных значений, а с точки зрения уменьшения значения функции потерь.

Для наискорейшего уменьшения функции потерь нам необходимо шагнуть в сторону её антиградиента по вектору предсказаний текущей композиции, то есть как раз таки в сторону вектора .

Это направление не обязательно совпадёт с шагом по направлению уменьшения разности предсказания и истинного значения. Например, может возникнуть гипотетическая ситуация, как на рисунке ниже:

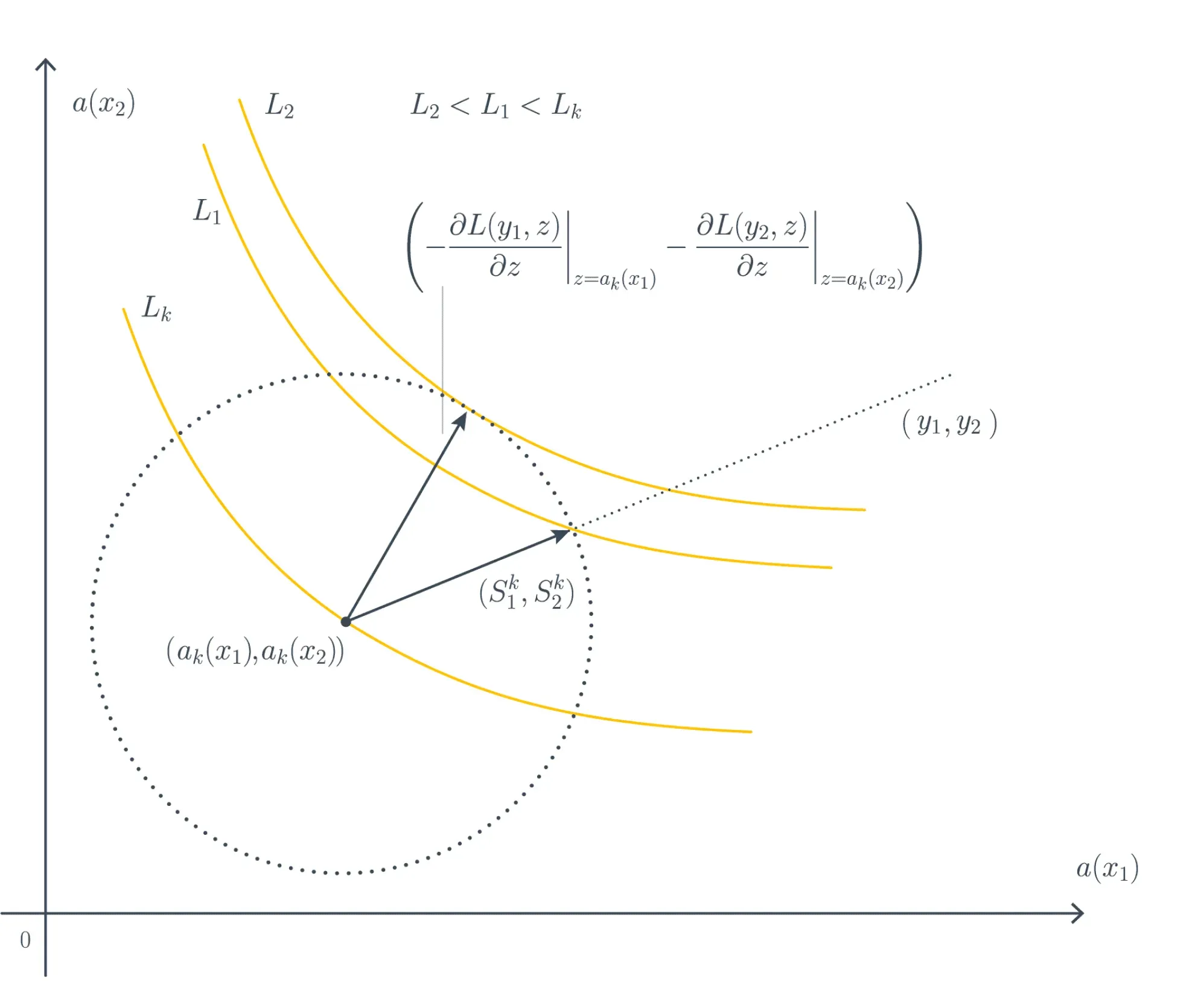
В изображённом примере рассматриваются два объекта — и . Текущее предсказание для них — , а окружность определяет варианты следующего шага: первый вариант — пойти в направлении , как делалось ранее; второй — пойти в направлении антиградиента. Также показаны линии уровня значений функции потерь.

Функция потерь в этом примере устроена таким образом, что , из-за чего шаг по антиградиенту оказывается более выгодным.

Движение в сторону антиградиента более выгодно с точки зрения минимизации функции потерь. Плюс оно позволяет справляться с ситуациями, когда явно посчитать остаток (разницу между целевым значением и предсказанием) не представляется возможным.

Один из таких примеров — задача ранжирования. В задаче ранжирования объекты в датасете разбиты на группы и нужно построить модель, по предсказаниям которой можно было бы «правильно» упорядочить документы в каждой группе (обычно по убыванию предсказания модели).

Это значит, что полученная по предсказаниям модели перестановка объектов в группе должна быть близка к идеальной по некоторой метрике.

Есть два способа:

• Первый — проставить каждому объекту число , по которому можно отсортировать объекты для получения идеальной перестановки. Это число можно рассматривать как таргет и обучать модель регрессии. В некоторых случаях это даже будет хорошо работать.

• Второй способ — задать набор пар объектов, которые обозначают их порядок относительно друг друга в идеальной перестановке. То есть пара означает, что объект с номером должен стоять раньше в перестановке, чем объект с номером .

Во втором способе у объектов нет таргетов, но дифференцируемая функция потерь есть. В библиотеке CatBoost она называется PairLogit и вычисляется по формуле:

где и — это предсказания модели на объектах и соответственно.

Градиент такой функции потерь посчитать можно, а разницу между предсказанием и истинным значением — нет.

Математическое обоснование

Попробуем записать наши интуитивные соображения более формально. Пусть — дифференцируемая функция потерь, а наш алгоритм представляет собой композицию базовых алгоритмов:

Мы «жадно» строим нашу композицию:

где вновь добавляемый базовый алгоритм обучается так, чтобы улучшить предсказания текущей композиции:

Модель выбирается так, чтобы минимизировать потери на обучающей выборке:

Для построения базовых алгоритмов на следующих шагах рассмотрим разложение Тейлора функции потерь до первого члена в окрестности точки

Избавившись от постоянных членов, мы получим следующую оптимизационную задачу:

Или в векторном виде:

где:

• — построчное применение базового алгоритма на всех строках ;
• — вектор градиентов функции потерь на шаге .

Поскольку суммируемое выражение — это скалярное произведение двух векторов, его значение минимизируют , пропорциональные значениям . Поэтому на каждой итерации базовые алгоритмы обучаются предсказывать значения антиградиента функции потерь по текущим предсказаниям композиции.

Итак, использованная нами интуиция шага в сторону «уменьшения остатка» удивительным образом привела к оптимальным смещениям в случае квадратичной функции потерь, но для других функций потерь это не так: для них смещение происходит в сторону антиградиента.

Обучение базового алгоритма

При построении очередного базового алгоритма мы решаем задачу регрессии с таргетом, равным антиградиенту функции потерь исходной задачи на предсказании .

Теоретически можно воспользоваться любым методом построения регрессионного дерева. Важно выбрать оценочную функцию , которая будет показывать, насколько текущая структура дерева хорошо приближает антиградиент. Её нужно будет использовать для построения критерия ветвления:

где:

• — значение функции в вершине ;
• , — значения в левом и правом сыновьях после добавления предиката;
• — количество элементов, пришедших в вершину.

Например, можно использовать следующие оценочные функции:

где:

• — предсказание дерева на объекте ;
• — значение антиградиента, на котором учится дерево;
• и — векторы с компонентами соответственно.

Функция представляет собой среднеквадратичную ошибку, а функция определяет близость через косинусное расстояние между векторами предсказаний и антиградиентов.

В итоге обучение базового алгоритма проходит в два шага:

1. По функции потерь вычисляется целевая переменная для обучения следующего базового алгоритма:

2. На обучающей выборке строится регрессионное дерево, минимизирующее выбранную оценочную функцию.

На практике

Поскольку для построения градиентного бустинга достаточно уметь считать градиент функции потерь по предсказаниям, с его помощью можно решать широкий спектр задач. В библиотеках градиентного бустинга даже реализована возможность создавать свои функции потерь: для этого достаточно уметь вычислять её градиент, зная истинные значения и текущие предсказания для элементов обучающей выборки.

Типичный градиентный бустинг имеет в составе несколько тысяч деревьев решений, которые необходимо строить последовательно. Построение решающего дерева на выборках типичного размера и современном железе, даже с учётом всех оптимизаций, требует небольшого, но всё-таки заметного времени (0,1–1 c), которое для всего ансамбля превратится в десятки минут. Это не так быстро, как обучение линейных моделей, но всё-таки значительно быстрее, чем обучение типичных нейросетей.

Проблема переобучения

Обучение композиции с помощью градиентного бустинга может привести к переобучению, если базовые алгоритмы слишком сложные. Например, если сделать решающие деревья слишком глубокими (более 10 уровней), то при обучении бустинга ошибка на обучающей выборке даже при довольно скромном может приблизиться к нулю, то есть предсказание будет почти идеальным, но на тестовой выборке всё будет плохо.

Возможные решения этой проблемы:

• во-первых, нужно упростить базовую модель, уменьшив глубину дерева (или применив какие-либо ещё техники регуляризации);

• во-вторых, мы можем ввести параметр, называемый темпом обучения (англ. learning rate), — :

Присутствие этого параметра означает, что каждый базовый алгоритм вносит относительно небольшой вклад во всю композицию. Если расписать сумму целиком, она будет иметь вид

Значение параметра обычно определяется эмпирически по входным данным. В библиотеке CatBoost темп обучения может быть выбран автоматически по набору данных. Для этого используется заранее обученная линейная модель, предсказывающая темп обучения по метапараметрам выборки данных: числу объектов, числу признаков и другим.

Темп обучения связан с количеством итераций градиентного бустинга. Чем ниже темп обучения, тем больше итераций потребуется для достижения того же качества на обучающей выборке.

Важность признаков

Отдельные деревья решений легко интерпретировать, просто визуализируя их структуру. Но в модели градиентного бустинга содержатся сотни деревьев, и поэтому её нелегко интерпретировать с помощью визуализации входящих в неё деревьев. При этом хотелось бы как минимум понимать, какие именно признаки в данных оказывают наибольшее влияние на предсказание композиции.

Можно сделать следующее наблюдение: признаки из верхней части дерева влияют на окончательное предсказание для большей доли обучающих объектов, чем признаки, попавшие на более глубокие уровни.

Таким образом, ожидаемая доля обучающих объектов, для которых происходило ветвление по данному признаку, может быть использована в качестве оценки его относительной важности для итогового предсказания. Усредняя полученные оценки важности признаков по всем решающим деревьям из ансамбля, можно уменьшить дисперсию такой оценки и использовать её для отбора признаков. Этот метод известен как среднее уменьшение примесей (англ. Mean Decrease in Impurity, MDI).

Существуют и другие методы оценки важности признаков для ансамблей: например, вычисление важности признаков (англ. Permutation Feature Importance, см. описание в sklearn) и множество разных подходов, предлагаемых в библиотеке CatBoost. Все эти техники отбора признаков применимы и для случайных лесов.

Реализации

Для общего развития имеет смысл посмотреть реализацию в sklearn, но на практике она весьма медленная и не такая уж «умная».

Примечание: помимо реализации, рекомендуем посмотреть раздел документации sklearn с теоретическими выкладками для градиентного бустинга.

Хороших реализаций градиентного бустинга на решающих деревьях (GBDT) как минимум три: LightGBM, XGBoost и CatBoost. Исторически они довольно сильно различались, но за последние годы успели скопировать друг у друга все хорошие идеи.

Форма деревьев

Одно из основных различий LightGBM, XGBoost и CatBoost — форма решающих деревьев.

LightGBM

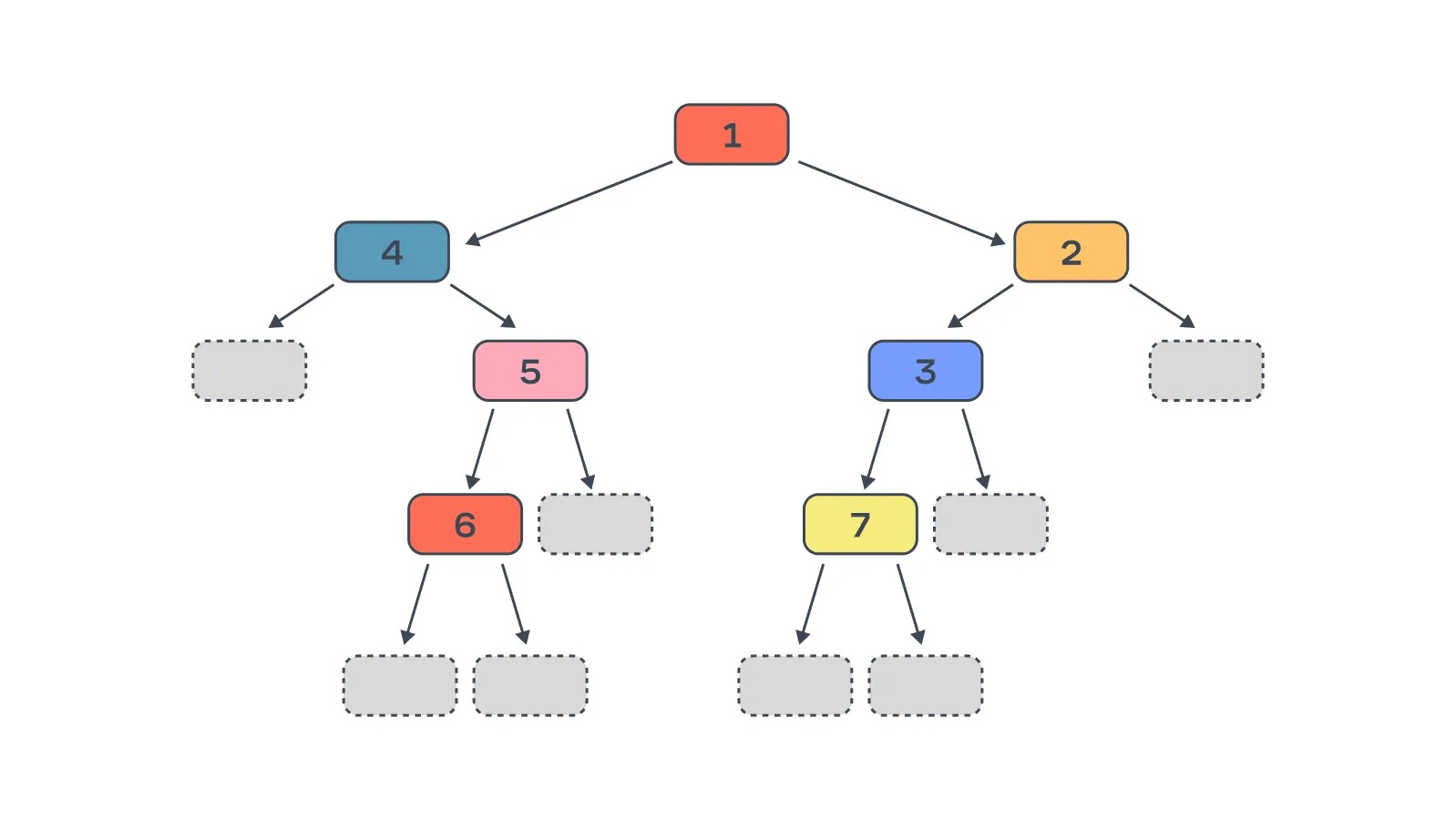
Принцип построения дерева: на каждом шаге делим вершину с наилучшим скором.

Основным критерием остановки выступает максимально допустимое количество вершин в дереве. Это приводит к тому, что деревья получаются несимметричными, то есть поддеревья могут иметь разную глубину. Например, левое поддерево может иметь глубину , а правое может разрастись до глубины .

С одной стороны, это позволяет быстро подогнаться под обучающие данные. С другой — бесконтрольный рост дерева в глубину неизбежно ведёт к переобучению, поэтому LightGBM позволяет, помимо количества вершин, ограничивать и максимальную глубину. Впрочем, это ограничение обычно всё равно выше, чем для XGBoost и CatBoost.

XGBoost

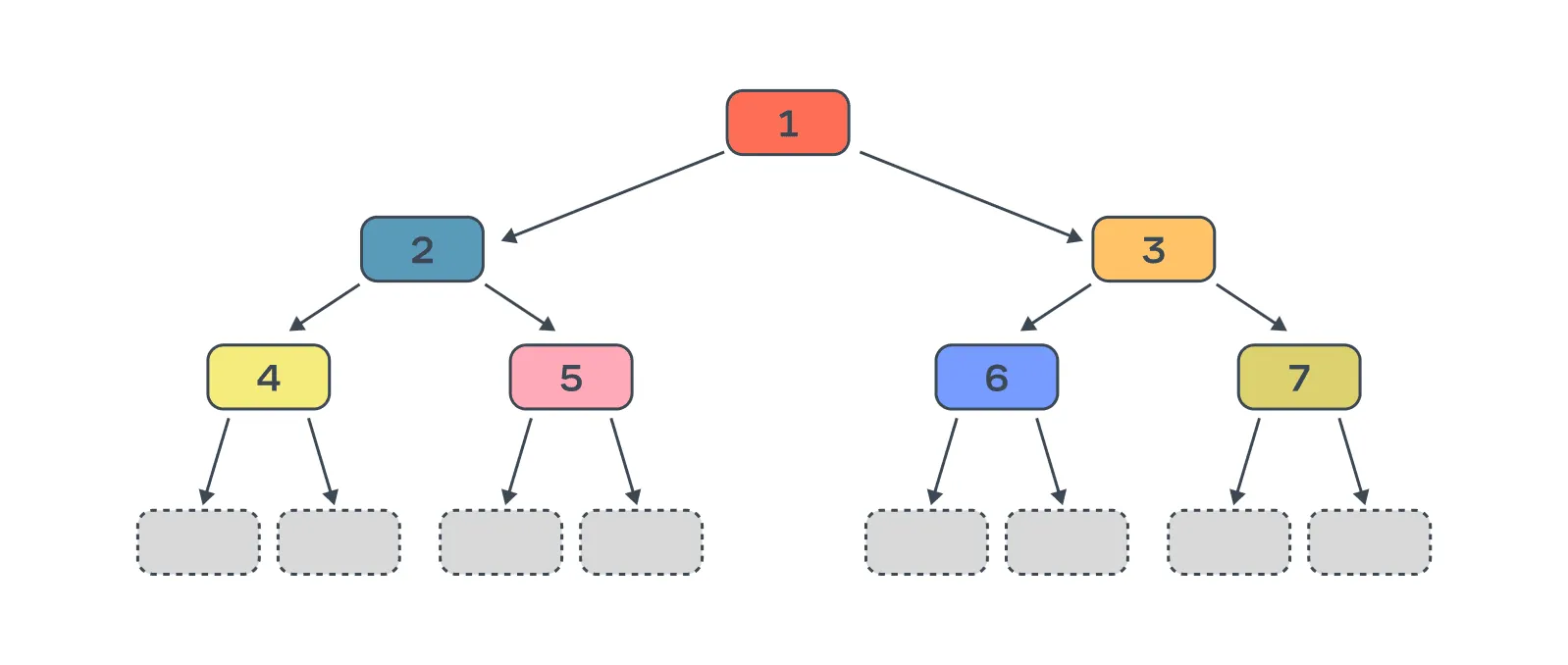
Принцип построения дерева: строим дерево последовательно, по уровням, до достижения максимальной глубины.

Отдельного ограничения на количество вершин нет, так как оно естественным образом получается из ограничения на глубину дерева.

В XGBoost деревья стремятся быть симметричными по глубине, и в идеале получается полное бинарное дерево, если это не противоречит другим ограничениям (например, ограничению на минимальное количество объектов в листе). Такие деревья обычно более устойчивы к переобучению.

CatBoost

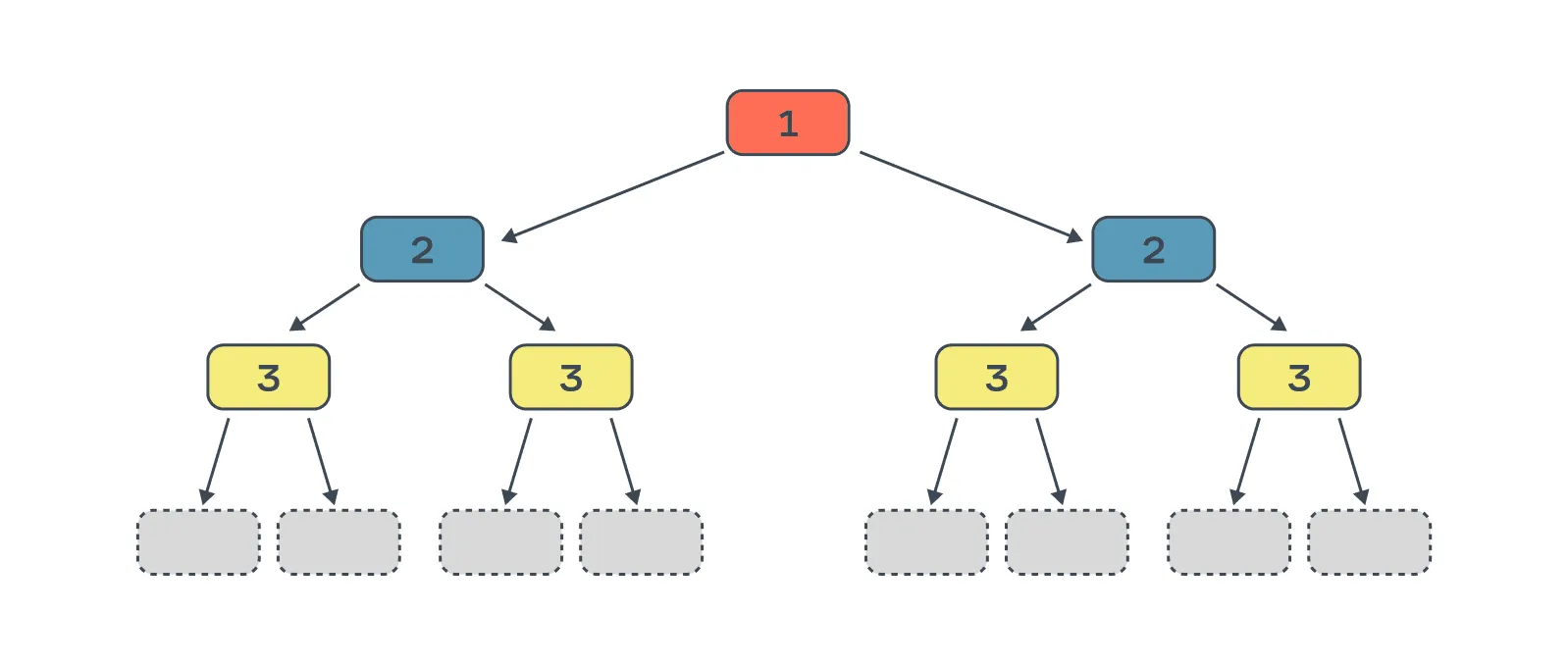
Принцип построения дерева: все вершины одного уровня имеют одинаковый предикат.

Одинаковые сплиты во всех вершинах одного уровня позволяют избавиться от ветвлений (конструкций if-else) в коде инференса модели с помощью битовых операций и получить более эффективный код, который в разы ускоряет применение модели, особенно в случае применения на батчах.

Кроме этого, такое ограничение на форму дерева выступает в качестве сильной регуляризации, что делает модель более устойчивой к переобучению. Основной критерий остановки, как и в случае XGBoost, — ограничение на глубину дерева. Однако, в отличие от XGBoost, в CatBoost всегда создаются полные бинарные деревья, несмотря на то что в некоторые поддеревья может не попасть ни одного объекта из обучающей выборки.

Заключение

Градиентный бустинг — это один из двух главных подходов, которые используются на практике (второй — это нейронные сети, конечно). Формально градиентный бустинг слабее и менее гибок, чем сети, но выигрывает в простоте настройки темпа обучения и применения, размере и интерпретируемости модели.

Во многих компаниях, так или иначе связанных с ML, он используется для всех задач, которые не связаны с однородными данными (картинками, текстами и так далее). Типичный поисковый запрос в Яндексе, выбор отеля на Booking.com или сериала на вечер в Netflix задействует несколько десятков моделей GBDT.

Впрочем, в будущем можно ожидать плавное исчезновение этого подхода, так как улучшение архитектур глубинного обучения и дальнейшее развитие железа нивелирует его преимущество по сравнению с нейросетями.

В следующем параграфе мы дадим рекомендации по практическому применению градиентного бустинга и иных методов, рассмотренных ранее.

---

В качестве практики предлагаем реализовать алгоритм в ноутбуке, а после сравнить свою имплементацию с существующими решениями.