Мотивация: метод моментов
Метод моментов — это ещё один способ, наряду с методом максимального правдоподобия, оценки параметров распределения по данным . Суть его в том, что мы выражаем через параметры распределения теоретические значения моментов нашей случайной величины, затем считаем их выборочные оценки , приравниваем их все друг к другу и, решая полученную систему, находим оценки параметров.
Можно доказать, что полученные оценки являются состоятельными, хотя могут быть смещены.
Пример 1. Оценим параметры нормального распределения с помощью метода моментов.
Теоретические моменты равны
Запишем систему:
Из неё очевидным образом находим
Легко видеть, что полученные оценки совпадают с оценками максимального правдоподобия
Пример 2. Оценим параметр логнормального распределения
при известном . Будет ли оценка совпадать с оценкой, полученной с помощью метода максимального правдоподобия?
Теоретическое математическое ожидание равно , откуда мы сразу находим оценку .
Теперь запишем логарифм правдоподобия:
Дифференцируя по и приравнивая производную к нулю, получаем
что вовсе не совпадает с оценкой выше.
Несколько приукрасив ситуацию, можно сделать вывод, что первые два выборочных момента позволяют если не править миром, то уверенно восстанавливать параметры распределений. А теперь давайте представим, что мы посчитали и , а семейство распределений пока не выбрали.
Как же совершить этот судьбоносный выбор? Давайте посмотрим на следующие три семейства и подумаем, в каком из них мы бы стали искать распределение, зная его истинные матожидание и дисперсию?
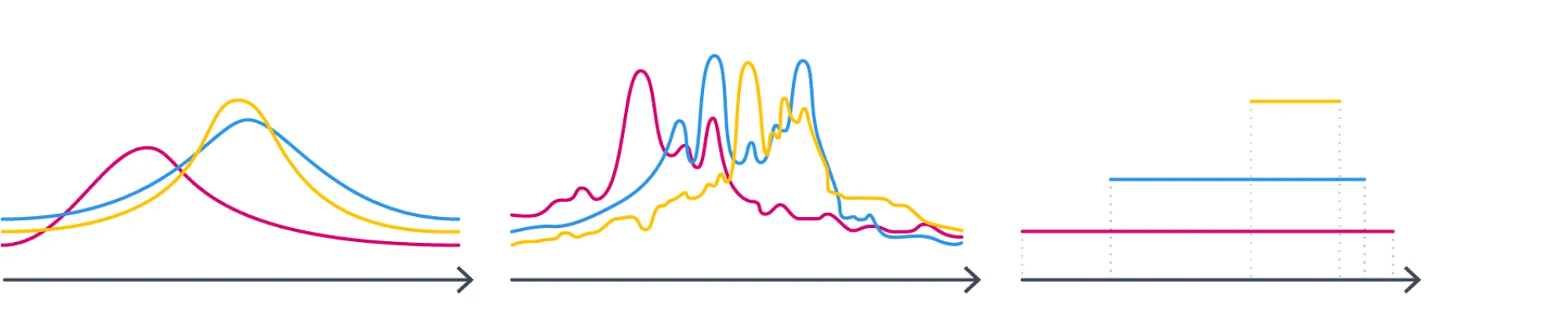
Почему-то хочется сказать, что в первом. Почему? Второе не симметрично — но почему мы так думаем? Если мы выберем третье, то добавим дополнительную информацию как минимум о том, что у распределения конечный носитель. А с чего бы? У нас такой инфомации вроде бы нет.
Общая идея такова: мы будем искать распределение, которое удовлетворяет только явно заданным нами ограничениям и не отражает никакого дополнительного знания о нём. Но чтобы эти нестрогие рассуждения превратить в формулы, придётся немного обогатить наш математический аппарат и научиться измерять количество информации.
Энтропия и дивергенция Кульбака-Лейблера
Измерять «знание» можно с помощью энтропии Шэннона. Она определяется как
для дискретного распределения и
для непрерывного. В классическом определении логарифм двоичный, хотя, конечно, варианты с разным основанием отличаются лишь умножением на константу.
Неформально можно представлять, что энтропия показывает, насколько сложно предсказать значение случайной величины. Чуть более строго — сколько в среднем бит нужно потратить, чтобы передать информацию о её значении.
Пример 1. Рассмотрим схему Бернулли с вероятностью успеха . Энтропия её результата равна
Давайте посмотрим на график этой функции:
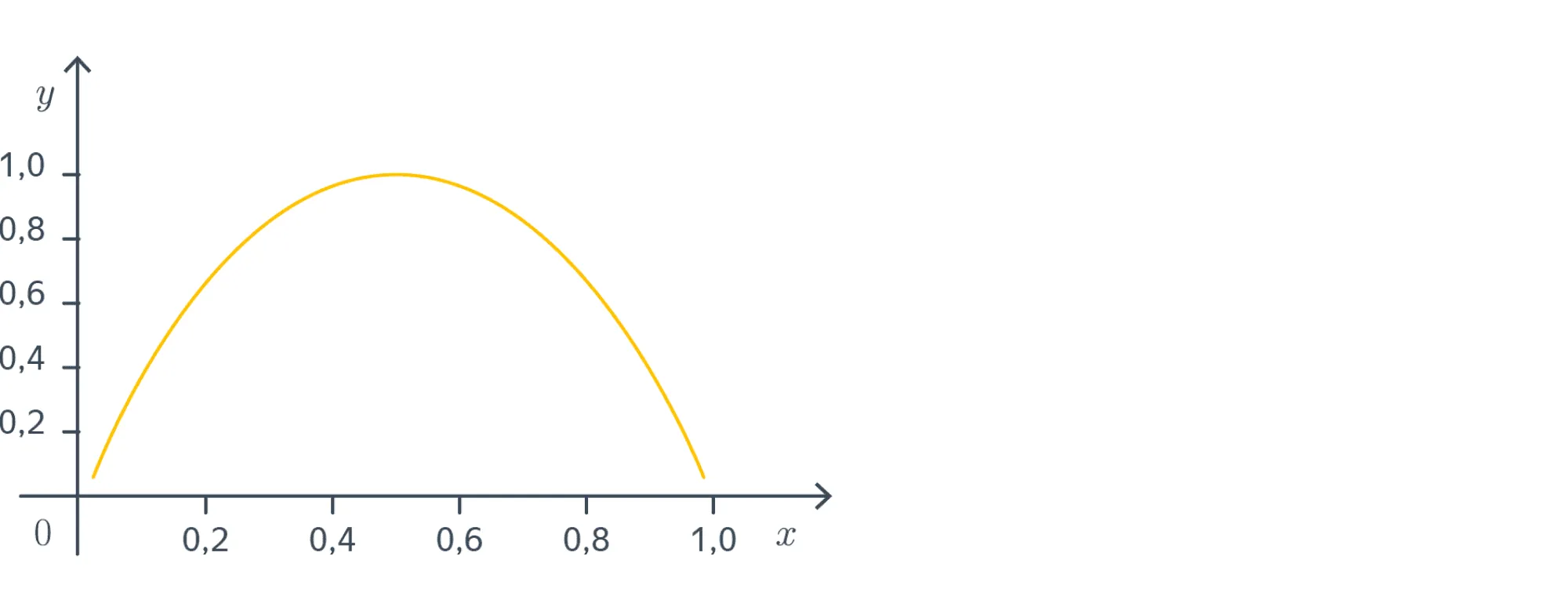
Минимальное значение (нулевое) энтропия принимает при . В самом деле, для такого эксперимента мы всегда можем наверняка сказать, каков будет его исход; обращаясь к другой интерпретации — чтобы сообщить кому-то о результате эксперимента, достаточно бит (ведь получатель сообщения и так понимает, что вышло).
Максимальное значение принимается в точке , что вполне соответствует тому, что при предсказать исход эксперимента сложнее всего.
Дополнение для ценителей математики.
Попробуем для этого простого примера объяснить, почему среднее число бит, необходимых для передачи информации об исходе эксперимента, выражается формулой с логарифмами.
Теперь пусть произвольно. Рассмотрим независимых испытаний ; среди них будет неудачных и удачных. Посчитаем, сколько бит потребуется, чтобы закодировать последовательность для известных и . Общее число таких последовательностей равно , а чтобы закодировать каждую достаточно будет бит — это количество информации, содержащееся во всей последовательности. Таким образом, в среднем, чтобы закодировать результат одного испытания необходимо
бит информации. Перепишем это выражение, использовав формулу Стирлинга :
Вот мы и вывели формулу энтропии!
Пример 2. Энтропия нормального распределения равна , и чем меньше дисперсия, тем меньше энтропия, что и логично: ведь когда дисперсия мала, значения сосредоточены возле матожидания, и они становятся менее «разнообразными».
Энтропия тесно связана с другим важным понятием из теории информации — дивергенцией Кульбака-Лейблера. Она определяется для как
в непрерывном случае и точно так же, но только с суммой вместо интеграла в дискретном.
Дивергенцию можно представить в виде разности:
Вычитаемое — это энтропия, которая, как мы уже поняли, показывает, сколько в среднем бит требуется, чтобы закодировать значение случайной величины. Уменьшаемое похоже по виду, и можно показать, что оно говорит о том, сколько в среднем бит потребуется на кодирование случайной величины с плотностью алгоритмом, оптимизированным для кодирования случайной величины .
Иными словами, дивергенция Кульбака-Лейблера говорит о том, насколько увеличится средняя длина кодов для значений , если при настройке алгоритма кодирования вместо использовать . Более подробно вы можете почитать, например, в этом посте.
Дивергенция Кульбака-Лейблера в некотором роде играет роль расстояния между распределениями. В частности, , причём дивергенция равна нулю, только если распределения совпадают почти всюду. Но при этом она не является симметричной: вообще говоря, .
Вопрос на подумать. Пусть — распределение, заданное на отрезке . Выразите энтропию через дивергенцию Кульбака-Лейблера с равномерным на отрезке распределением .
Ответ (не открывайте сразу; сначала подумайте сами!)
Распишем дивергенцию:
Аналогичное соотношение можно выписать и для распределения, заданного на конечном множестве.
Принцип максимальной энтропии
Теперь наконец мы готовы сформулировать, какие распределения мы хотим искать.
Принцип максимальной энтропии. Среди всех распределений на заданном носителе , удовлетворяющих условиям , ..., , где — некоторые функции, мы хотим иметь дело с тем, которое имеет наибольшую энтропию.
В самом деле, энтропия выражает нашу меру незнания о том, как ведёт себя распределение, и чем она больше — тем более «произвольное распределение», по крайней мере, в теории.
Давайте рассмотрим несколько примеров, которые помогут ещё лучше понять, почему некоторые распределения так популярны:
Пример 1. На конечном множестве наибольшую энтропию имеет равномерное распределение (носитель — конечное множество из элементов, других ограничений нет).
Доказательство: Пусть , — некоторое распределение, — равномерное. Запишем их дивергенцию Кульбака-Лейблера:
Так как дивергенция Кульбака-Лейблера всегда неотрицательна, получаем, что . При этом равенство возможно, только если распределения совпадают.
Пример 2. Среди распределений, заданных на всей вещественной прямой и имеющих заданные матожидание и дисперсию наибольшую энтропию имеет нормальное распределение .
Доказательство: Пусть — некоторое распределение, . Запишем их дивергенцию Кульбака-Лейблера:
Так как дивергенция Кульбака-Лейблера всегда неотрицательна, получаем, что . При этом равенство возможно, только если распределения и совпадают почти всюду, а с точки зрения теории вероятностей такие распределения различать не имеет смысла.
Пример 3. Среди распределений, заданных на множестве положительных вещественных чисел и имеющих заданное матожидание наибольшую энтропию имеет показательное распределение с параметром (его плотность равна ).
Все хорошо знакомые нам распределения, не правда ли? Проблема в том, что они свалились на нас чудесным образом. Возникает вопрос, можно ли их было не угадать, а вывести как-нибудь? И как быть, если даны не эти конкретные, а какие-то другие ограничения?
Оказывается, что при некоторых не очень обременительных ограничениях ответ можно записать с помощью распределений экспоненциального класса. Давайте же познакомимся с ними поближе.
Экспоненциальное семейство распределений
Говорят, что семейство распределений относится к экспоненциальному классу, если оно может быть представлено в следующем виде:
где — вектор вещественнозначных параметров (различные значения которых дают те или иные распределения из семейства), , — некоторая вектор-функция, и, разумеется, сумма или интеграл по равняется единице. Последнее, в частности, означает, что
(или сумма в дискретном случае).
Пример 1. Покажем, что нормальное распределение принадлежит экспоненциальному классу. Для этого мы должны представить привычную нам функцию плотности
в виде
Распишем
Определим
Если теперь всё-таки честно выразить через (это мы оставляем в качестве лёгкого упражнения), то получится
В данном случае функция просто равна единице.
Пример 2. Покажем, что распределение Бернулли принадлежит экспоненциальному классу. Для этого попробуем преобразовать функцию вероятности (ниже принимает значения или ):
Теперь мы можем положить , , и всё получится. Единственное, что смущает, — это то, что компоненты вектора линейно зависимы. Хотя это не является формальной проблемой, но всё же хочется с этим что-то сделать. Исправить это можно, если переписать
и определить уже минимальное представление с , — мы ведь уже сталкивались с этим выражением, когда изучали логистическу регрессию, не так ли?
Вопрос на подумать. Принадлежит ли к экспоненциальному классу семейство равномерных распределений на отрезках ? Казалось бы, да: так как:
В чём может быть подвох?
Ответ (не открывайте сразу; сначала подумайте сами!)
Нет, не принадлежит. Давайте вспомним, как звучало определение экспоненциального семейства. Возможно, вас удивило, что там было написано не «распределение относится», а «семейство распределений относится».
Это важно: ведь семейство определяется именно различными значениями , и если нас интересует семейство равномерных распределений на отрезках, определяемое параметрами и , то они не могут быть в функции , они должны быть под экспонентой, а экспонента ни от чего не может быть равна индикатору.
При этом странное и не очень полезное семейство с нулём параметров, состоящее из одинокого распределения можно считать относящимся к экспоненциальному классу: ведь для него формула
будет работать.
Как мы увидели, к экспоненциальным семействам относятся как непрерывные, так и дискретные распределения. Вообще, к ним относится большая часть распределений, которыми Вам на практике может захотеться описать .
В том числе:
- нормальное;
- распределение Пуассона;
- экспоненциальное;
- биномиальное, мультиномиальное (с фиксированным числом испытаний);
- геометрическое;
- -распределение;
- бета-распределение;
- гамма-распределение;
- распределение Дирихле.
К экспоненциальным семействам не относятся, к примеру:
- равномерное распределение на отрезке;
- -распределение Стьюдента;
- распределение Коши;
- смесь нормальных распределений.
MLE для семейства из экспоненциального класса
Возможно, вас удивил странный и на первый взгляд не очень естественный вид . Но всё не просто так: оказывается, что оценка максимального правдоподобия параметров распределений из экспоненциального класса устроена очень интригующе.
Запишем функцию правдоподобия выборки :
Её логарифм равен
Дифференцируя по , получаем
Тут нам потребуется следующая
Лемма.
Доказательство:
Как мы уже отмечали в прошлом пункте:
Следовательно,
Кстати, можно ещё доказать, что
Приравнивая к нулю и применяя лемму, мы получаем, что
Таким образом, теоретические матожидания всех компонент должны совпадать с их эмпирическими оценками, а метод максимального правдоподобия совпадает с методом моментов для в качестве моментов.
И в следующем пункте выяснится, что распределения из семейств, относящихся к экспоненциальному классу, это те самые распределения, которые имеют максимальную энтропию из тех, что имеют заданные моменты .
**Пример.**Рассмотрим вновь логнормальное распределение:
Как видим, логнормальное распределение тоже из экспоненциального класса. Вас может это удивить: ведь выше мы обсуждали, что для него метод моментов и метод максимального правдоподобия дают разные оценки.
Но никакого подвоха тут нет: мы просто брали не те моменты. В данном случае , , их матожидания и надо брать; тогда для параметров, получаемых из MLE, должно выполняться
Матожидания в левых частых мы должны выразить через параметры — и нам для этого совершенно не обязательно что-то интегрировать! В самом деле:
Теорема Купмана-Питмана-Дармуа
Теперь мы наконец готовы сформулировать одно из самых любопытных свойств семейств экспоненциального класса.
В следующей теореме мы опустим некоторые не очень обременительные условия регулярности. Просто считайте, что для хороших дискретных и абсолютно непрерывных распределений, с которыми вы в основном и будете сталкиваться, это так.
Теорема. Пусть — распределение, причём — вектор длины и для некоторых фиксированных , . Тогда распределение обладает наибольшей энтропией среди распределений с тем же носителем, для которых , . При этом оно — единственное с таким свойством: в том смысле, что любое другое распределение, обладающее этим свойством, совпадает с ним почти всюду.
Идея обоснования через оптимизацию.
Мы приведём рассуждение для дискретного случая; в абсолютно непрерывном рассуждения будут по сути теми же, только там придётся дифференцировать не по переменным, а по функциям, и мы решили не ввергать вас в мир вариационного исчисления.
В дискретном случае у нас есть счётное семейство точек , и распределение определяется счётным набором вероятностей принимать значение . Мы будем решать задачу
Запишем лагранжиан:
Продифференцируем его по :
Приравнивая это к нулю, получаем
Числитель уже ровно такой, как и должен быть у распределения из экспоненциального класса. Разберёмся со знаменателем.
Легко видеть, что условие заведомо выполнено (ведь тут сплошные экспоненты), так что его можно было выкинуть из постановки задачи оптимизации или, что то же самое, положить . Параметр находится из условия , а точнее, выражается через остальные , что позволяет записать знаменатель в виде .
Идея доказательства «в лоб».
Как и следовало ожидать, оно ничем не отличается от того, как мы доказывали максимальность энтропии у равномерного или нормального распределения. Пусть — ещё одно распределение, для которого
для всех . Тогда
Таким образом, , причём по уже не раз использованному нами свойству дивергенции Кульбака-Лейблера из будет следовать то, что и совпадают почти всюду.
Рассмотрим несколько примеров:
Пример 1. Среди распределений на множестве неотрицательных целых чисел с заданным математическим ожиданием найдём распределение с максимальной энтропией.
В данном случае у нас лишь одна функция , которая соответствует фиксации матожидания . Плотность будет вычисляться только в точках , и будет иметь вид
В этой формуле уже безошибочно угадывается геометрическое распределение с . Параметр можно подобрать из соображений того, что математическое ожидание равно . Матожидание геометрического распределения равно , так что . Окончательно,
Пример 2. Среди распределений на всей вещественной прямой с заданным математическим ожиданием найдём распределение с максимальной энтропией.
А сможете ли вы его найти? Решение под катом.
Теория говорит нам, что его плотность должна иметь вид
но интеграла экспоненты не существует, то есть применение «в лоб» теоремы провалилось. И неспроста: если даже рассмотреть все нормально распределённые случайные величины со средним , их энтропии, равные не ограничены сверху, то есть величины с наибольшей энтропией не существует.



