В этом параграфе мы на примере задачи распознавания изображений познакомимся со свёрточными нейронными сетями, уже ставшими стандартом в области. Для начала мы разберёмся, с какого рода данными придётся работать, затем попробуем решить задачу «в лоб» при помощи знакомых вам полносвязных сетей и поймём, чем это чревато. А после чего рассмотрим свёртки и попробуем выработать нужную интуицию.
Формат данных
Картинки в большинстве случаев представляют собой упорядоченный набор пикселей, где каждый пиксель — это вектор из трех «каналов»: интенсивность красного, интенсивность зелёного, интенсивность синего.

Каждая интенсивность характеризуется числом от 0 до 1, но для привычных нам изображений этот интервал равномерно дискретизирован для экономии памяти, чтобы уместиться в 8 бит (от 0 до 255). При этом нулевая интенсивность (0, 0, 0), соответствует чёрному цвету, а максимальная интенсивность (255, 255, 255) — белому.
Когда мы наблюдаем изображение на мониторе компьютера, мы видим эти пиксели «уложенными» в строки одинаковой длины (человек не сможет воспринять картинку, вытянутую в один вектор). Длину каждой такой строки называют шириной W картинки, а количество строк — высотой H. Резюмирую, мы можем рассматривать картинку, как тензор HxWx3, состоящий из чисел uint8.

Существует множество разных форматов хранения картинок: вместо трех интенсивностей мы можем использовать триплет «оттенок, насыщенность, интенсивность», а сами картинки хранить, например, как тензор CxHxW.
MLP
Наверное, самый простой способ построить нейронную сеть для решения задачи классификации на наших данных — это «развернуть» нашу картинку в вектор, а затем использовать обычную многослойную сеть с кросс-энтропией в качестве лосса.
Однако, такой подход имеет несколько недостатков.
Недостаток №1: количество параметров
В первом слое у нас получается HxWxCxCout параметров, где Cout — это количество нейронов в первом слое. Если поставить Cout слишком маленьким, мы рискуем потерять много важной информации, особенно, если рассматривать картинки размером, например, 1920x1080.
Если же выставить Cout большим, рискуем получить слишком много параметров (а это только первый слой), а с этим и все вытекающие проблемы — переобучение, сложность оптимизации и так далее.
Недостаток №2: структура данных никак не учитывается.
Что здесь имеется в виду под «структурой»? Попробуем объяснить на примере. Для этого рассмотрим картинку щеночка:

Если мы сдвинем картинку на несколько пикселей, то мы все еще будем уверены в том, что это щенок:

Точно также мы останемся неизменны в своем мнении, если картинку отмасштабировать:

или повернуть/развернуть:


Получается, что нейронная сеть должна «сама» понять, что ее ответ должен быть инвариантен к описанным преобразованиям. Но, обычно, это достигается за счет увеличения количества нейронов в скрытых слоях (как мы можем помнить из universal approximation theorem), что и так для нас — головная боль из-за первого пункта.
С частью этих проблем нам поможет новый «строительный блок» — свёртка. О ней в следующем разделе.
Свёртки
Строгое определение свёртки мы дадим ниже, а вначале разберёмся в мотивации.
Давайте попробуем решить хотя бы проблему инвариантности к сдвигу. Щенок может быть где угодно на картинке, и мы не можем наверняка сказать, в какой части изображения наша модель «лучше всего» научилась видеть щенков. Поэтому для надёжного предсказания будет логично посдвигать картинку на все возможные смещения (пустоты заполним нулями):

Затем для каждого смещения мы предскажем вероятность наличия щенка на картинке. Получившиеся предсказания можно уже агрегировать как удобно: среднее, максимум и так далее.
Давайте взглянем на эту операцию под другим углом. Рассмотрим картинку, размером в 3 раза превышающую оригинальную, в центре которой находится наше изображение щеночка:

Возьмём окно размером с исходную картинку, и будем его сдвигать на все возможные смещения внутри нового изображения:

Легко видеть, что получается то же самое, как если бы мы картинку сдвигали относительно окна.
Представим себе самую простую модель, основанную на данном принципе — что-то вроде ансамбля линейных. Каждую из сдвинутых картинок вытянем в вектор и скалярно умножим на вектор весов (для простоты один и тот же для всех сдвигов) — получим линейный оператор, для которого есть специальное имя — свёртка.
Это один из важнейших компонент в свёрточных нейронных сетях. Веса свёртки, упорядоченные в тензор (в нашем случае размерности HxWx3), составляют её ядро. Область картинки, которая обрабатывается в текущий момент, обычно называется окном свёртки.
Обратите внимание, что обычно такие свёртки называются двумерными — так как окно свёртки пробегает по двум измерениям картинки (при этом все цветовые каналы участвуют в вычислениях).
Следующая картинка поможет разобраться (внимание: на ней нет изображения весов оператора):

Каждый «кубик» на картинке — это число. Большой черный тензор слева — это изображение щеночка . Фиолетовым на нем выделено окно, из которого мы достаем все пиксели и разворачиваем в вектор (аналогично операции flatten в numpy) .
Далее этот вектор умножается на вектор весов класса «щенок» , и получается число — логит интересующего класса. Добавив остальные классы, получим матрицу весов — прямо как в мультиномиальной логистической регрессии. Эту операцию мы повторяем для каждого возможного сдвига окна свёртки.
Результаты домножения удобно бывает скомпоновать в двумерную табличку, которую при желании можно трактовать, как некоторую новую картинку (в серых тонах, потому что канал уже только один). Воспользуемся этим, чтобы получше осознать, что происходит в ходе свёртки.
Вопрос на подумать. Какой геометрический смысл имеет свёртка с ядром
А с ядром
Ответ (не открывайте сразу; сначала подумайте сами!)
Первая свёртка усредняет каждый пиксель с соседними, и изображение размывается. Смысл второй можно грубо описать так: пиксели из однородных участков изображения слабеют, тогда как контрастные точки, напротив, усиливаются. Можно сказать, что такая свёртка выделяет границы. Проиллюстрируем работу этих ядер на примере небольшого изображения в серых тонах:

В донейросетевую эпоху различные свёртки играли существенную роль в обработке изображений, и сейчас мы видим, почему.
Вопрос на подумать. На краях картинок из ответа к предыдущему вопросу заметны тёмные рамки. Что это такое? Откуда они берутся?
Ответ (не открывайте сразу; сначала подумайте сами!)
Их появление связано с особенностями обработки свёртками краёв изображения. Вообще, есть несколько стратегий борьбы с краями. Например:
- Дополнить изображение по краям нулями. Когда мы будем рассматривать окна свёртки с центрами в крайних пикселях, они будут захватывать эти нули. Такая свёртка будет превращать изображение размером
HxWx3в изображение размеромHxW, без уменьшения размера. Но так как нули соответствуют чёрному цвету, это будет вносить определённые изменения в крайние пиксели результата. Именно благодаря этому у картинок из предыдущего вопроса на подумать по краям появились тёмные рамки. - Разрешить только такие окна, которые целиком лежат внутри изображения. Это будет приводить к падению размера. Например, для окна размером
5x5картинка размеромHxWx3превратится в картинку размером(H-2)x(W-2).
Решив проблему обеспечения устойчивости к сдвигу картинки и имея на руках наш огромный свёрточный фильтр, давайте попробуем теперь справиться с первой проблемой — количество параметров. Самое простое, что можно придумать, — это уменьшить размер окна с HxW до, допустим, kxk (обычно нечётное и ). В этом случае получается радикальное снижение количества параметров и сложности вычислений.

К сожалению, с таким подходом возникает новая проблема: предсказание для какого-то окна никак не учитывает контекст вокруг него. Получается, мы можем получить разумные предсказания только в случае, если распознаваемый объект обладает признаками, которые «помещаются» в окно свёртки (например, лого автомобиля при классификации марок машин), либо объекты заметно отличаются по своей текстуре (шерсть кошки vs кирпич, например).
На картинке ниже сделана попытка изобразить проблему:

Область картинки, на которую «смотрит» наша нейронная сеть, называется receptive field — и про него приходится часто думать в задачах компьютерного зрения.
Давайте и мы подумаем, как его можно было бы увеличить, не увеличивая размер ядра. Вспомним, что в нашей нейронке сейчас есть только один слой, сразу предсказывающий класс. Выглядит так, что мы можем применить уже знакомую технику стекинга слоев: пусть на первой стадии мы делаем разных свёрток с фильтрам размером kxk. Результаты каждой свёртки можно упорядочить в виде новой «картинки», а из этих «картинок» сложить трёхмерный тензор. Получаем так называемую карту признаков размером HxWxC_1.
Применим к ней поэлементно нелинейность и воспользуемся K новыми свёртками для получения предсказаний для каждого пикселя. На таком шаге получается, что наш receptive field для финальных нейронов вырос от kxk до (2k-1)x(2k-1) (пояснение на картинке).
Повторяя такую операцию, мы можем добиться, чтобы наши финальные нейроны уже могли «видеть» почти всю нужную информацию для хорошего предикта. Более того, у нас возникает меньшее количество параметров и падает сложность вычислений в сравнении с использованием одной большой полносвязной сети.
Как это схематично выглядит:

Промежуточный тензор , полученный при помощи свёрток, можно себе представить, как новую картинку, у которой уже каналов.
На следующей картинке можно отследить, как меняется receptive field в зависимости от глубины:

На картинке схематично изображен «плоский» двумерный тензор (количество каналов = 1), к которому последовательно применили три свёртки 3x3. В каждом случае рассматривается пиксель в центре. Каждый соответствующий тензор помечен, как . Если рассматривать первую свёртку (), то размер receptive field равен размеру е окна = 3.
Рассмотрим вторую свёртку . В ее вычислении участвуют пиксели из квадрата 3х3, причём каждый из них, в свою очередь, был получен при помощи предыдущей свёртки . Получается, что receptive field композиции свёрток — это объединение receptive fields свёртки по всем пикселям из окна свёртки , образуя новый, размером 5x5. Аналогичные рассуждения можно повторить и для всех последующих свёрток.
Ещё один способ увеличить receptive field — это использовать dilated convolution, в которых окно свёртки (то есть те пиксели картинки, на которые умножается ядро) не обязано быть цельным, а может идти с некоторым шагом (вообще говоря, даже разным по осям H и W).
Проиллюстрируем, как будет выглядеть окно для обычной свёртки и для свёртки с шагом dilation=2:
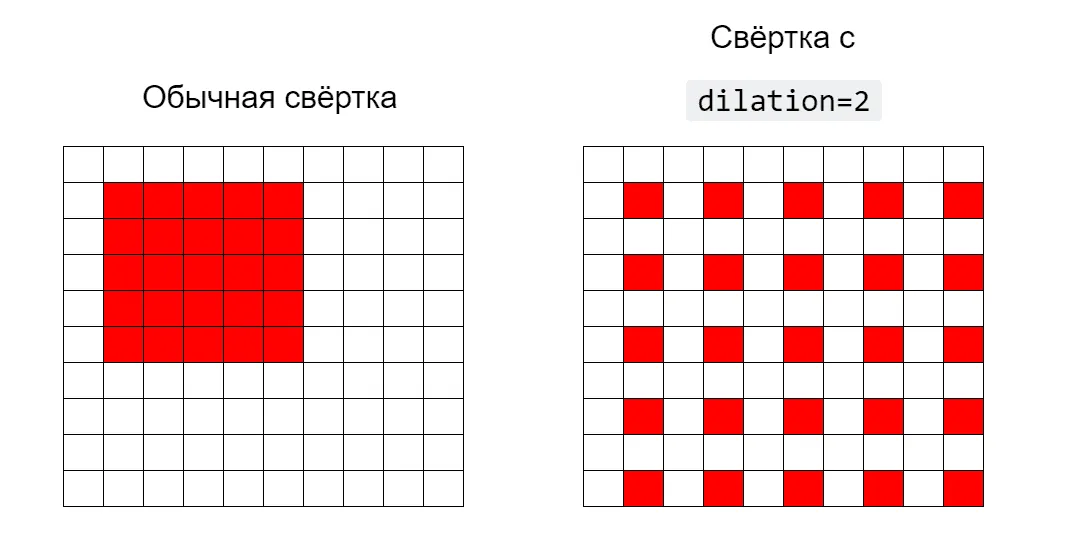
Если установить параметр dilation=(1,1), получится обычная свёртка.
Итак, свёртки помогли нам решить сразу две проблемы: устойчивости к сдвигу и минимизации числа параметров. Теперь давайте попробуем определить оператор более формально.
Формальное определение свёртки

Вопрос на подумать. Пусть у нас есть тензор размером HxWxC_{in}, к которому одновременно применяется свёрток, размер окна каждой равен kxk. Посчитайте количество обучаемых параметров. Как изменится формула, если к свёртке добавить смещение (bias)? Во сколько раз изменится количество параметров, если увеличить размер окна в 2 раза? А если увеличить количество каналов и в два раза? А если увеличить размер входного тензора в 2 раза по высоте и ширине?
Вопрос на подумать. Оцените количество операций сложений-умножений для предыдущего упражнения. Как оно поменяется, если увеличить в два раза размер окна? Количество каналов? Размер входного тензора?
Вопрос на подумать. Пусть последовательно применяется свёрток . Посчитайте размер receptive field для последнего оператора.
Свёртки не только для изображений
Нетрудно видеть, что аналоги двумерной свёртки можно определить и для тензоров другой размерности, в любой ситуации, когда для нас актуально поддерживать устойчивость модели к сдвигам данных. Например, это актуально для работы с текстами. Обычно текст разбивается на последовательные токены (например, на слова или какие-то subword units), и каждому из этих токенов ставится в соответствие вектор (более подробно об этом вы можете почитать в параграфе про работу с текстами или в разделе про вложения слов учебника по NLP Лены Войта).

Представим теперь, что мы хотим определить, позитивно или негативно окрашен этот текст. Мы можем предположить, что эмоциональная окраска локальна и может проявляться на любом участке текста, и тогда нам нужна модель, которая может «посмотреть» отдельно на каждый последовательный фрагмент текста некоторой длины. И здесь тоже может сработать свёртка:

Существуют свёртки и для тензоров более высокой размерности, например, для видео (где прибавляется ещё координата «время»).
Поворот, отражение, масштабирование
А что делать с остальными проблемами: поворотом, отражением, масштабированием? К сожалению, на момент написания параграфа (вторая половина 2021 года), автору не было известно об успешном опыте решения этих проблем в архитектуре сети. При этом оказывается, что приведенного оператора уже достаточно, чтобы нейронная сеть могла хорошо обобщать на невиданные ранее картинки (лишь бы свёрток было больше и сеть глубже).
В качестве потенциально интересного (но пока не проявившего себя на практике) направления исследований можно упомянуть капсульные нейросети. Кроме того, вам может быть интересно познакомиться с геометрическим глубинным обучением. В качестве короткого введения рекомендуем посмотреть вот этот keynote с ICLR 2021, которое ставит своей целью исследование общих принципов, связывающих устойчивость к различным преобразованием и современные нейросетевые архитектуры (авторы сравнивают свои идеи с эрлангенской программой Феликса Кляйна — отсюда название).
Свёрточный слой и обратное распространение ошибки
Поговорим о том, как через свёрточный слой протекают градиенты. Нам нужно будет научиться градиент по выходу превращать в градиент по входу и в градиент по весам из ядра.
Начнём с иллюстрации для одномерной свёртки с одним входным каналом, ядром длины с дополнением по бокам нулями. Заметим, что её можно представить в виде матричного умножения:
Обозначим последнюю матрицу через , а ядро свёртки через . Что происходит с градиентом при переходе через матричное умножение, мы уже отлично знаем. Градиент по весам равен
Разберёмся, что из себя представляет умножение на справа. Эта матрица имеет вид
Она тоже соответствует свёртке, только:
- с симметричным исходному ядром ;
- с дополнением вектора нулями (это как раз соответствует неполным столбцам: можно считать, что «выходящие» за границы матрицы и отсутствующие в ней элементы умножаются на нули).
Вопрос на подумать. Поменяется ли что-нибудь, если исходный вектор не дополнять нулями?
Общий случай
Рассмотрим теперь двумерную свёртку, для простоты нечётного размера и без свободного члена
- Продифференцируем по :
Разберёмся с производной . Во всей большой сумме из определения свёртки для элемент может встретиться в позициях при , и всевозможных , причём это возможно лишь если , (для всех остальных производная по нулевая). Соответствующий коэффициент при будет равен . Таким образом, производная будет иметь вид:
Легко заметить, что это тоже свёртка, но поскольку индексы в и в стоят с разными знаками, получаем, что
- Продифференцируем по :
В формуле для элемент может встретиться в позициях , для , , с коэффициентами (для любых ). Значит, производная будет иметь вид:
В этой формуле тоже нетрудно узнать свёртку:
Вопрос на подумать. Если всё-таки есть свободные члены, как будет выглядить градиент по ?
Остальные важные блоки свёрточных нейронных сетей
Наигравшись с нашими мысленными экспериментами, давайте обратимся к опыту инженеров и исследователей, который копился с 2012 года – alexnet. Он поможет нам разобраться с тем, как эффективней всего строить картиночные нейронки. Здесь будут перечислены самые важные (на момент написания и по мнению автора) блоки.
Max pool
Каждая из свёрток очередного свёрточного слоя — это новая карта признаков для нашего изображения, и нам, конечно, хотелось бы, чтобы таких карт было побольше: ведь это позволит нам выучивать больше новых закономерностей.
Но для картинок в высоком разрешении это может быть затруднительно: слишком уж много будет параметров. Выходом оказалось использование следующей эвристики: сначала сделаем несколько свёрток с каналами, а затем как-нибудь уменьшим нашу карту признаков в 2 раза и одновременно увеличим количество свёрток во столько же.
Посчитаем, как в таком случае изменится число параметров: было , стало , то есть, ничего не изменилось, а количество фильтров удвоилось, что приводит к выучиванию более сложных зависимостей.
Осталось разобраться, как именно можно понижать разрешение картинки. Тривиальный способ — взять все пиксели с нечетными индексами. Такой подход будет работать, но, как может подсказать здравый смысл, выкидывать пиксели — значит терять информацию, а этого не хотелось бы делать.
Здесь есть много вариантов: например, брать среднее/максимум по обучаемым весам в окне 2x2, которое идет по карте признаков с шагом 2. Экспериментально выяснилось, что максимум — хороший выбор, и, в большинстве архитектур, используют именно его. Обратите внимание, что максимум берется для каждого канала независимо.
Еще одно преимущество — увеличение receptive field. Получается, что он увеличивается в 2 раза:

Операция понижения разрешения со взятием максимума в окне называется max pooling, а со взятием среднего — average pooling.
Вопрос на подумать. Как будет преобразовываться градиент во время error backpropagation для maxpool с окном и шагом 2x2? А для average pool?
Кстати, ещё один способ уменьшать размер карт признаков по ходу применения свёрточной сети — использование strided convolution, в которых ядро свёртки сдвигается на каждом шаге на некоторое большее единицы число пикселей (возможно, разное для осей H и W; обычная свёртка получается, если установить параметр stride=(1,1)).

Global average pool
Как свёрточные слои, так и пулинг превращают картинку в «стопку» карт признаков. Но если мы решаем задачу классификации или регрессии, то в итоге нам надо получить число (или вектор логитов, если речь про многоклассовую классификацию).
Один из способов добиться этого — воспользоваться тем, что свёртка без дополнения нулями и пулинг уменьшают размер карты признаков, и в итоге при должном терпении и верном расчёте мы можем получить тензор 1x1xC (финальные, общие признаки изображения), к которому уже можно применить один или несколько полносвязных слоёв. Или же можно, не дождавшись, пока пространственные измерения схлопнутся, «растянуть» всё в один вектор и после этого применить полносвязные слои (именно так, как мы не хотели делать, не правда ли?). Примерно так и происходило в старых архитектурах (alexnet, vgg).
Вопрос на подумать. Попробуйте соорудить конструкцию из свёточных слоёв и слоёв пулинга, превращающую изображение размера 128x128x3 в тензор размера 1x1xC.
Но у такого подхода есть как минимум один существенный недостаток: для каждого размера входящего изображения нам придётся делать новую сетку.
Позднее было предложено следующее: после скольких-то свёрточных слоёв мы будем брать среднее вдоль пространственных осей нашего последнего тензора и усреднять их активации, а уже после этого строить MLP. Это и есть Global Average Pooling. У такого подхода есть несколько преимуществ:
- радикально меньше параметров;
- теперь мы можем применять нейронку к картинку любого размера;
- мы сохраняем «магию» инвариантности предсказаний к сдвигам.

Residual connection
Оказывается, что, если мы будем бесконтрольно стекать наши свёртки, то, несмотря на использование relu и batch normalization, градиенты все равно будут затухать, и на первых слоях будут почти нулевыми. Интересное решение предлагают авторы архитектуры resnet: давайте будем «прокидывать» признаки на предыдущем слое мимо свёрток на следующем:

Таким образом получается, что градиент доплывет даже до самых первых слоев, что существенно ускоряет сходимость и качество полученной модели. Вопрос: почему именно сумма? Может, лучше конкатенировать? Авторы densenet именно такой подход и предлагают (с оговорками), получая результаты лучше, чем у resnet. Однако, такой подход получается вычислительно сложным и редко используется на практике.
Регуляризация
Несмотря на наши ухищрения со свёртками, в современных нейронных сетях параметров все равно оказывается больше, чем количество картинок. Поэтому часто оказывается важным использовать различные комбинации регуляризаторов, которых уже стало слишком много, чтобы все описывать в этом параграфе, так что мы рассмотрим лишь несколько наиболее важных.
Классические
Почти все регуляризаторы, которые использовались в классической машинке и полносвязных сетях, применимы и здесь: l1/l2, dropout и так далее.
Вопрос на подумать. Насколько разумно использовать dropout в свёрточных слоях? Как можно модифицировать метод, чтобы он стал «более подходящим»?
Аугментации
Это один из самых мощных инструментов при работе с картинками. Помогает, даже если картинок несколько тысяч, а нейронная сеть с миллионами параметров. Мы уже выяснили, что смещение\поворот\прочее не меняют (при разумных параметрах) факта наличия на картинке того или иного объекта.
На самом деле, есть огромное множество операций, сохраняющих это свойство:
- сдвиги, повороты и отражения;
- добавление случайного гауссового шума;
- вырезание случайной части картинки (cutout);
- перспективные преобразования;
- случайное изменение оттенка\насыщенности\яркости для всей картинки;
- и многое другое.
Пример хорошой библиотеки с аугментациями: Albumentations.
Label smoothing
Часто оказывается, что нейронная сеть делает «слишком уверенные предсказания»: 0.9999 или 0.00001. Это становится головной болью, если в нашей разметке есть шум — тогда градиенты на таких объектах могут сильно портить сходимость.
Исследователи пришли к интересной идее: давайте предсказывать не one-hot метку, а ее сглаженный вариант. Итак, пусть у нас есть классов:
Обычно берут . Тем самым модель штрафуется за слишком уверенные предсказания, а шумные лейблы уже не вносят такого большого вклада в градиент.
Mixup
Самый интересный вариант. А что будет, если мы сделаем выпуклую комбинацию двух картинок и их лейблов:

где обычно семплируется из какого-нибудь Бета распределения. Оказывается, что такой подход заставляет модель выучивать в каком-то смысле более устойчивые предсказания, так как мы форсируем некую линейность в отображении из пространства картинок в пространство лейблов. На практике часто оказывается, что это дает значимое улучшение в качестве модели.
Бонус №1: знаковые архитектуры в мире свёрточных нейронных сетей для задачи классификации изображений
Дисклеймер: это мнение одного автора. Приведённые в этом разделе вехи связаны преимущественно с архитектурами моделей, а не способом их оптимизации.
Здесь перечислены знаковые архитектуры, заметно повлиявшие на мир свёрточных нейронных сетей в задаче классификации картинок (и не только). К каждой архитектуре указана ссылка на оригинальную статью, а также комментарий автора параграфа с указанием ключевых нововведений. Значение метрики error rate на одном из влиятельных датасетов imagenet указано для финального ансамбля из нейросетей, если не указано иное.
Зачем это полезно изучить (вместе с чтением статей)? Основных причин две:
- Общее развитие. Полезно понимать, откуда взялись и чем мотивированы те или иные компоненты.
- Этот вопрос задают на собеседовании, когда не знают, что еще спросить 😃
lenet (1998)
7 слоев
Первая свёрточная нейронная сеть, показавшая SOTA (State Of The Art) результаты на задаче классификации изображений цифр MNIST. В архитектуре впервые успешно использовались свёрточные слои с ядром 5x5. В качестве активации использовался tanh, а вместо max pool в тот момент использовался average.
alexnet (2012)
11 слоев
Первая CNN (Convolutional Neural Network), взявшая победу на конкурсе imagenet. Автор предложил использовать ReLU вместо сигмоид (чтобы градиенты не затухали) и популяризовал max-pool вместо average. Что самое важное, обучение модели было перенесено на несколько GPU, что позволило обучать достаточно большую модель за относительное небольшое время (6 дней на двух видеокартах того времени). Также автор обратил внимание, что глубина нейросети важна, так как выключение хотя бы одного слоя стабильно ухудшало качество на несколько процентов.
network in network (2013)
В статье не привели интересных SOTA результатов, но зато ввели два очень популярных впоследствии модуля. Первый — это GAP (Global Average Pooling), который стоит после последнего свёрточного слоя и усредняет все активации вдоль пространственных осей. Второй — стекинг 1x1 свёрток поверх 3x3, что эквивалентно тому, что вместо линейной свёртки используется полносвязный слой.
vgg (2014)
19 слоев
Авторы предложили декомпозировать большие свёртки (5x5, 7x7 и выше) на последовательное выполнение свёрток 3x3 с нелинейностями между ними. Впоследствии, за нечастым исключением, свёртки 3x3 стали стандартом в индустрии (вместе со свёртками 1x1).
googleLeNet aka Inception (2014)
22 слоя
Ввели inception слой, просуществовавший довольно продолжительное время. Сейчас сам слой уже не используется, но идея лежащая в его основе, эксплуатируется. Идея следующая: будем параллельно применять свёртки с разным пространственными размерами ядер, чтобы можно было одновременно обрабатывать как low-, так и high-level признаки. Еще полезной для сообщества оказалась идея с dimensionality reduction: перед тяжелой операцией поставим свёртку 1x1, чтобы уменьшить количество каналов и кратно ускорить вычисление.
batch normalization (2015)
Авторы внедрили вездесущую batch normalization, которая стабилизирует сходимость, позволяя увеличить шаг оптимизатора и скорость сходимости. Применив идею к архитектуре inception, они превзошли человека на imagenet.
kaiming weight initialization (2015)
В статье предложили использовать инициализацию весов, берущую во внимание особенность активации ReLU (в предыдущих работах предполагалось, что , что, очевидно, нарушается для ). Применение этой и других «свистелок» на VGG19 позволило существенно уменьшить ошибку на imagenet.
ResNet (2015)
152 слоя
Архитектура, которая на момент написания этого параграфа до сих пор бейзлайн и отправная точка во многих задачах. Основная идея — использование skip connections, что позволило градиенту протекать вплоть до первых слоев. Благодаря этому эффекту получилось успешно обучать очень глубокие нейронные сети, например, с 1202 слоями (впрочем, результаты на таких моделях менее впечатляющие, чем на 152-слойной). После этой статьи также стали повсеместно использоваться GAP и уменьшение размерности свёртками 1x1.
MobileNet (2017)
Очень популярная модель для быстрого инференса (на мобильных устройствах или gpu). По качеству хоть и немного проигрывает «монстрам», но в индустрии, оказывается, зачастую этого достаточно (особенно если брать последние варианты модели).
Основная деталь — это использование depthwise convolutions: параллельный стекинг свёрток 3x3x1x1 — то есть таких, в которых вычисление для каждого канала просходит только на основе признаков одного канала. Чтобы скомбинировать фичи между каналами, используется классическая 1x1 свёртка.
EfficientNet (2019)
Одна из первых моделей, полученных при помощи NAS (Neural Architecture Search), которая взяла SOTA на imagenet. После этого, модели, где компоненты подбирались вручную, уже почти не показывали лучших результатов на классических задачах.
Бонус №2: не классификацией единой
Свёрточными нейронными сетями можно решать большой спектр задач, например:
- Сегментация. Если убрать в конце слои GlobalAveragePool или flatten, то можно делать предсказания для каждого пикселя в отдельности (подумайте, что делать, если в сети есть maxpool) — получаем сегментацию картинки. Проблема — долгая и дорогая разметка.
- Детекция. Часто намного дешевле получить разметку объектов обрамляющими прямоугольниками. Здесь уже можно для каждого пикселя предсказывать размеры прямоугольника, который обрамляет объект, к которому принадлежит пиксель. Проблемы — нужен этап агрегации прямоугольников + много неоднозначностей во время разметки + много эверистик на всех этапах + данных нужно больше.
- Понимание видео. Добавляем в тензор новый канал — временной, считаем четырехмерные свёртки — и получаем распознавание сцен на видео.
- Metric learning. Часто мы не можем собрать все интересующие нас классы, например, в задаче идентификации человека по лицу (или товара на полке). В этом случае используют такой трюк: научим модель в некотором смысле (обычно по косиносному расстоянию) разделять эмбеддинги существующих классов (уникальных людей). Если на руках была репрезентативная выборка, то модель, скорее всего (а обычно — всегда), выучит генерировать дискриминативные эмбеддинги, которые уже позволят различать между собой ранее невиданные лица.
- и многое другое
Итого
Мы разобрались, что для картинок эффективно использовать свёрточные фильтры в качестве основных операторов. Выяснили, какие основные блоки есть почти в каждой картиночной нейронной сети и зачем они там нужны. Разобрались, какие методы регуляризаторы сейчас самые популярные и какая за ними идея.
И наконец — рассмотрели знаковые архитектуры в мире свёрточных нейронных сетей.