4.1. Вероятностный подход в ML

В этом разделе мы посмотрим на те же самые модели машинного обучения, но с другой стороны: будем интерпретировать их как вероятностные.

В первом параграфе мы расскажем, как обращаться с вероятностными моделями, и покажем, что привычный вам подбор параметров модели с помощью минимизации функции потерь соответствует подбору параметров методом максимального правдоподобия. Это даст возможность транслировать в мир ML известные результаты о свойствах оценок максимального правдоподобия, но в то же время и обнажит их недостатки. Благодаря этому мы сможем по-новому взглянуть на логистическую регрессию и с новым пониманием сформулировать её обобщение — generalized linear model (GLM).

По ходу дела мы обнаружим, что большинство классификаторов, хоть и делают вид, что предсказывают корректные вероятности, на самом деле вводят в заблуждение.

В третьем параграфе мы поговорим о том, как проверить отклонение предсказанных значений от истинных вероятностей и как поправить ситуацию.

Далее мы обсудим генеративный подход к классификации и разберём несколько примеров генеративных моделей, после чего перейдём к байесовскому подходу оценивания параметров, который, хоть зачастую и трудно осуществим вычислительно, однако обладает большей теоретической стройностью. Он позволяет оценивать распределение параметров и предсказаний (например, уверенность в нашей оценке), а кроме того — даёт нам возможность измерить качество модели, не прибегая к проверке на тестовой выборке.

Если вы готовы — давайте приступим!

Случайность как источник несовершенства моделиСлучайность как источник несовершенства модели

Практически любая наша модель — несовершенна. Но объяснять это несовершенство можно по-разному.

Представим, что мы решаем задачу регрессии : например, пытаемся по университетским оценкам выпускника предсказать его годовую зарплату. Ясно, что точная зависимость у нас не получится как минимум потому, что мы многого не знаем о выпускнике: куда он пошёл работать, насколько он усерден, как у него с soft skills и так далее. Как же нам быть?

Первый вариант — просто признать, что мы не получим идеальную модель, но постараться выучить оптимальную, насколько это возможно. То есть приблизить таргет предсказаниями наилучшим образом с точки зрения какой-то меры близости, которую мы подберём из экспертных соображений.

Так мы получаем простой инженерный подход к машинному обучению: есть формула, в которой присутствуют некоторые параметры (), есть формализация того, что такое «приблизить» (функция потерь) — и мы бодро решаем задачу оптимизации по параметрам.

Второй вариант — свалить вину за неточности наших предсказаний на случайность. В самом деле: если мы что-то не можем измерить, то для нас это всё равно что случайный фактор. В постановке задачи мы заменяем приближённое равенство на точное

Например, это может быть аддитивный шум (чаще всего так и делают):

где — некоторая случайная величина, которая представляет этот самый случайный шум. Тогда получается, что для каждого конкретного объекта соответствующий ему истинный таргет — это сумма и конкретной реализации шума .

При построении такой модели мы можем выбирать различные распределения шума, кодируя тем самым, какой может быть ошибка. Чаще всего выбирают гауссовский шум: с некоторой фиксированной дисперсией — но могут быть и другие варианты.

Проиллюстрируем, как ведут себя данные, подчиняющиеся закону , :

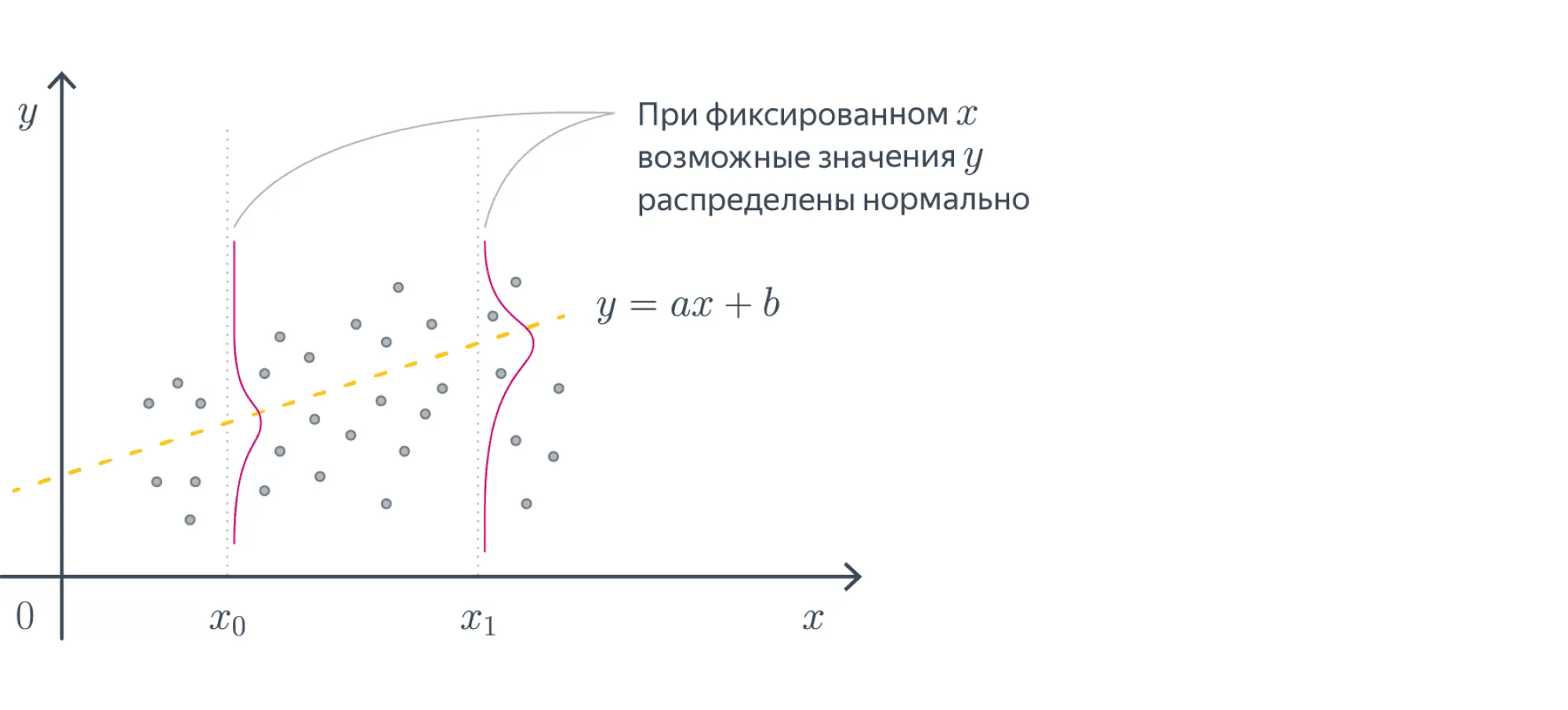
Вопрос на подумать. Зачем человеку может прийти в голову предположить, что в модели линейной регрессии шум имеет распределение Лапласа? А распределение Коши? Чем свойства таких моделей будут отличаться от свойств модели с нормальным шумом?

Ответ (не открывайте сразу; сначала подумайте сами!)

Давайте посмотрим, как выглядят плотности этих трёх распределений:

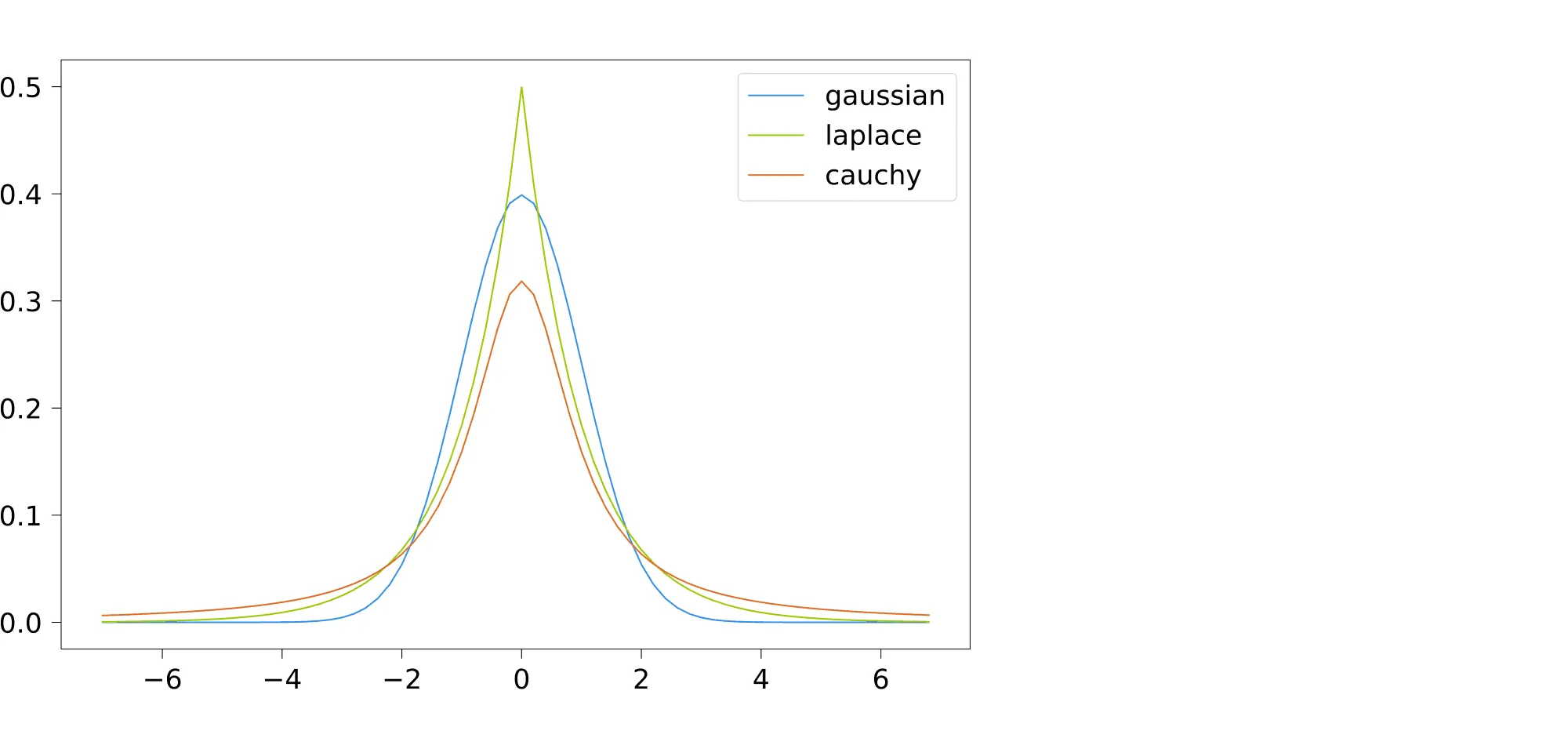
Распределение Лапласа имеет «более тяжёлые хвосты», чем нормальное: это значит, что плотность медленнее падает с удалением от среднего. Таким образом, этому распределению могут подчиняться данные, в которых имеются выбросы. Если не гнаться за строгостью, можно сказать, что модель с нормальным шумом будет пытаться объяснить выбросы, меняя под них , тогда как лапласовский шум потерпит их, не подгоняя .

У распределения Коши хвосты «ещё более тяжёлые», что, в теории, даёт возможность модели с таким шумом описывать даже ещё более шумные данные.

Проиллюстрируем датасеты, сгенерированные из моделей с каждым из типов шума: нормальным, лапласовским и Коши.

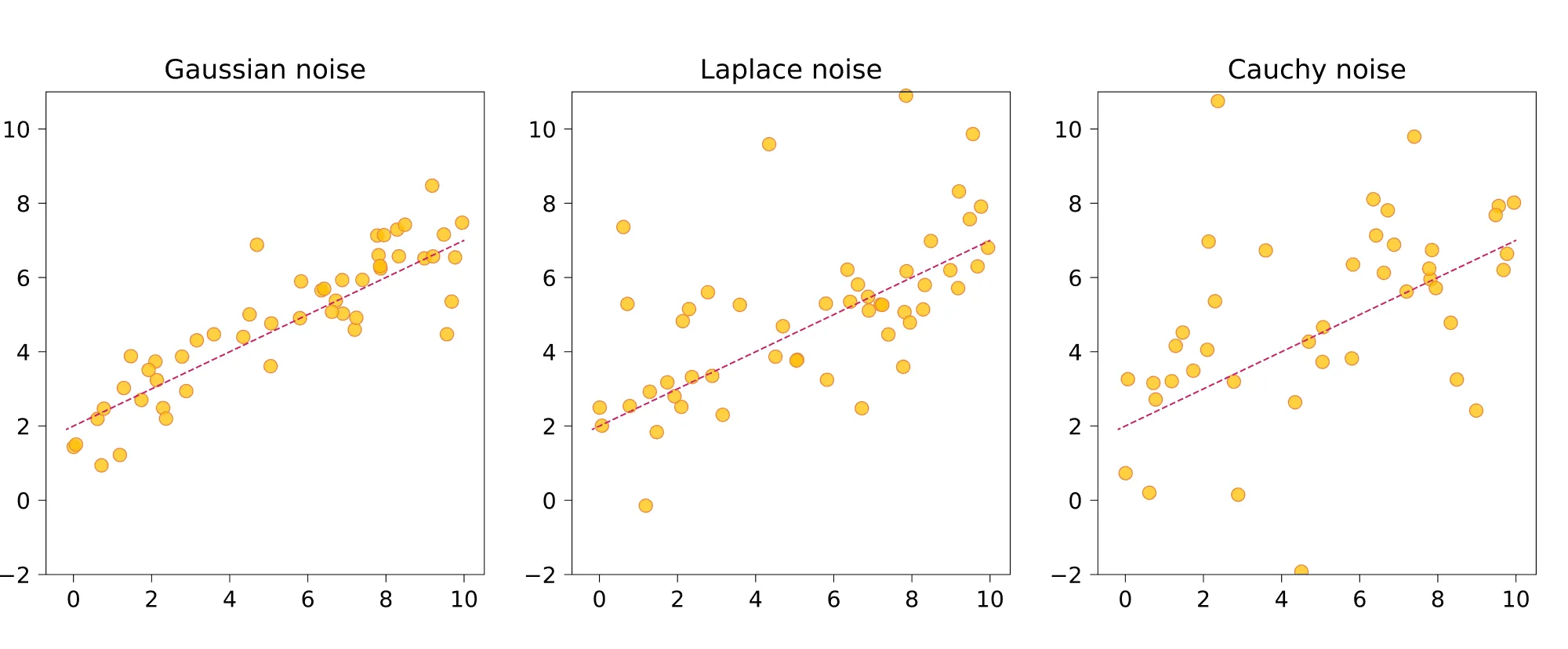
Как вы могли заметить, в каждом из подходов после того, как мы зафиксировали признаки (то есть координаты ), остаётся своя степень свободы: в инженерном это выбор функции потерь, а в вероятностном — выбор распределения шума.

Дальше в этом параграфе мы увидим, что на самом деле эти два подхода глубинным образом связаны между собой, причём выбор функции потерь — это в некотором смысле то же самое, что выбор распределения шума.

Условное распределение на таргет, непрерывный случайУсловное распределение на таргет, непрерывный случай

Допустим, что мы исследуем вероятностную модель таргета с аддитивным шумом

где — некоторая функция, не обязательно линейная с (неизвестными пока) параметрами , а — случайный шум с плотностью распределения . Для каждого конкретного объекта значение — это просто константа, но оно превращается в случайную величину, зависящую от (и ещё от , на самом деле).

Таким образом, можно говорить об условном распределении

Для каждого конкретного и распределение соответствующего — это просто , ведь .

Пример. Рассмотрим вероятностную модель , где . Тогда для фиксированного имеем . Поскольку — константа, мы получаем

Это можно записать и так:

где выражение справа — это значение функции плотности нормального распределения с параметрами в точке . В частности, .

Более сложные вероятностные моделиБолее сложные вероятностные модели

На самом деле, мы можем для нашей задачи придумывать любую вероятностную модель , не обязательно вида .

Представьте, что мы хотим предсказывать точку в плоскости штанг, в которую попадает мячом бьющий по воротам футболист. Можно предположить, что она имеет нормальное распределение со средним (цель удара), которое определяется ситуацией на поле и состянием игрока, и некоторой дисперсией (то есть скалярной ковариационной матрицей), которая тоже зависит от состояния игрока и ещё разных сложных факторов, которые мы объявим случайными.

Состояние игрока — это сложное понятие, но, вероятно, мы можем выразить его, зная пульс, давление и другие физические показатели. В свою очередь, ситуацию на поле можно описать, как функцию от позиций и движений других игроков, судьи и зрителей — но всего не перечислишь, поэтому нам снова придётся привлекать случайность. Таким образом, мы получаем то, что называется графической моделью:

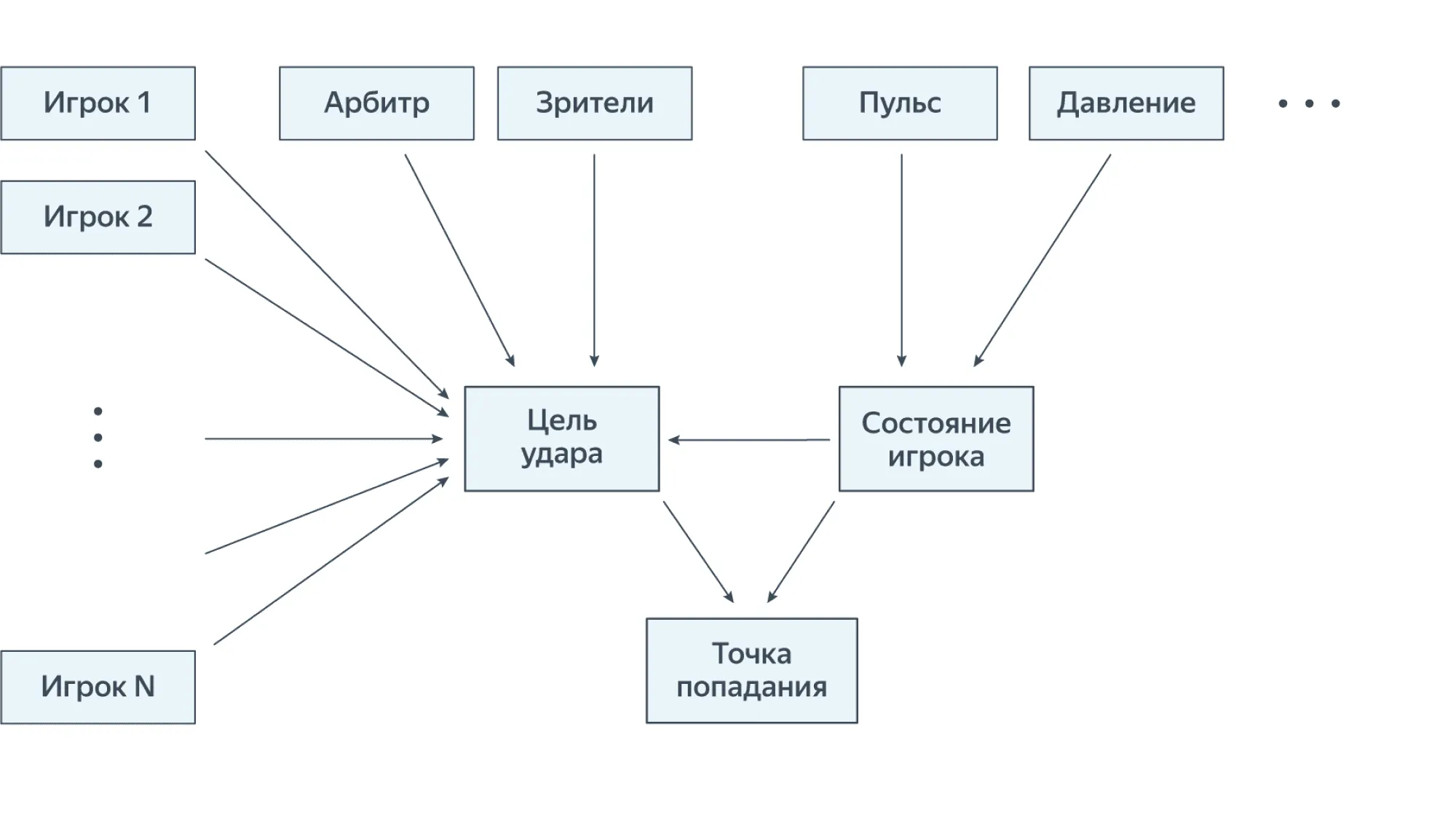
Здесь стрелки означают статистические зависимости, а отсутствие стрелок — допущение о статистической независимости. Конечно же, это лишь допущение, принятое нами для ограничения сложности модели: ведь пульс человека и давление взаимосвязаны, равно как и поведение различных игроков на поле. Но мы уже обсуждали, что каждая модель, в том числе и вероятностная, является лишь приблизительным отражением бесконечно сложного мира. Впрочем, если у нас много вычислительных ресурсов, то никто не мешает нам попробовать учесть и все пропущенные сейчас зависимости.

Расписав всё по определению условной вероятности, мы получаем следующую вероятностную модель:

в которой, конечно же, мы должны все вероятности расписать через какие-то понятные и логически обоснованные распределения — но пока воздержимся от этого.

Оценка максимального правдоподобия = оптимизация функции потерьОценка максимального правдоподобия = оптимизация функции потерь

Мы хотим подобрать такие значения параметров , для которых модель была бы наиболее адекватна обучающим данным. Суть метода максимального правдоподобия (maximum likelihood estimation) состоит в том, чтобы найти такое , для которого вероятность (а в данном, непрерывном, случае плотность вероятности) появления выборки была бы максимальной, то есть

Величина называется функцией правдоподобия (likelihood). Если мы считаем, что все объекты независимы, то функция правдоподобия распадается в произведение:

Теперь, поскольку перемножать сложно, а складывать легко (и ещё поскольку мы надеемся, что раз наши объекты всё-таки наблюдаются в природе, их правдоподобие отлично от нуля), мы переходим к логарифму функции правдоподобия:

эту функцию мы так или иначе максимизируем по , находя оценку максимального правдоподобия .

Как мы уже обсуждали выше, , то есть

Максимизация функции правдоподобия соответствует минимизации

а это выражением можно интерпретировать, как функцию потерь. Вот и оказывается, что подбор параметров вероятностей модели с помощью метода максимального правдоподобия — это то же самое, что «инженерная» оптимизация функции потерь. Давайте посмотрим, как это выглядит в нескольких простых случаях.

Пример. Давайте предположим, что наш таргет связан с данными вот так:

где , то есть

Случайная величина получается из шума сдвигом на постоянный вектор , так что она тоже распределена нормально с той же дисперсией и со средним

Правдоподобие выборки имеет вид

Логарифм правдоподобия можно переписать в виде

Постоянными слагаемыми можно пренебречь, и тогда оказывается, что максимизация этой величины равносильна минимизации

Мы получили обычную квадратичную функцию потерь. Итак, обучать вероятностную модель линейной регрессии с нормальным шумом — это то же самое, что учить «инженерную» модель с функцией потерь MSE.

Вопрос на подумать. Какая вероятностная модель соответствует обучению линейной регрессии с функцией потерь MAE

Предсказание в вероятностных моделяхПредсказание в вероятностных моделях

Теперь представим, что параметры подобраны, и подумаем о том, как же теперь делать предсказания.

Рассмотрим модель линейной регрессии

Если известен, то для нового объекта соответствующий таргет имеет вид

Таким образом, дан нам не точно, а в виде распределения (и логично: ведь мы оговорились выше, что ответы у нас искажены погрешностью, проинтерпретированной, как нормальный шум). Но что делать, если требуют назвать конкретное число? Кажется логичным выдать условное матожидание , тем более что оно совпадает с условной медианой и условной модой этого распределения.

Если же медиана, мода и математическое ожидание различаются, то можно выбрать что-то из них с учётом особенностей задачи. Но на практике в схеме чаще всего рассматривают именно симметричные распределения с нулевым матожиданием, потому что для них совпадает с условным матожиданием и является логичным точечным предсказанием.

Приведём пример. Допустим шум был бы из экспоненциального распределения. Тогда была бы условным минимумом распределения. В принципе, можно придумать задачу, для которой такая постановка (предсказание минимума) была бы логичной. Но это всё же довольно экзотическая ситуация. Приводим для сравнения модели с нормальным, лапласовским и экспоненциальным шумом:

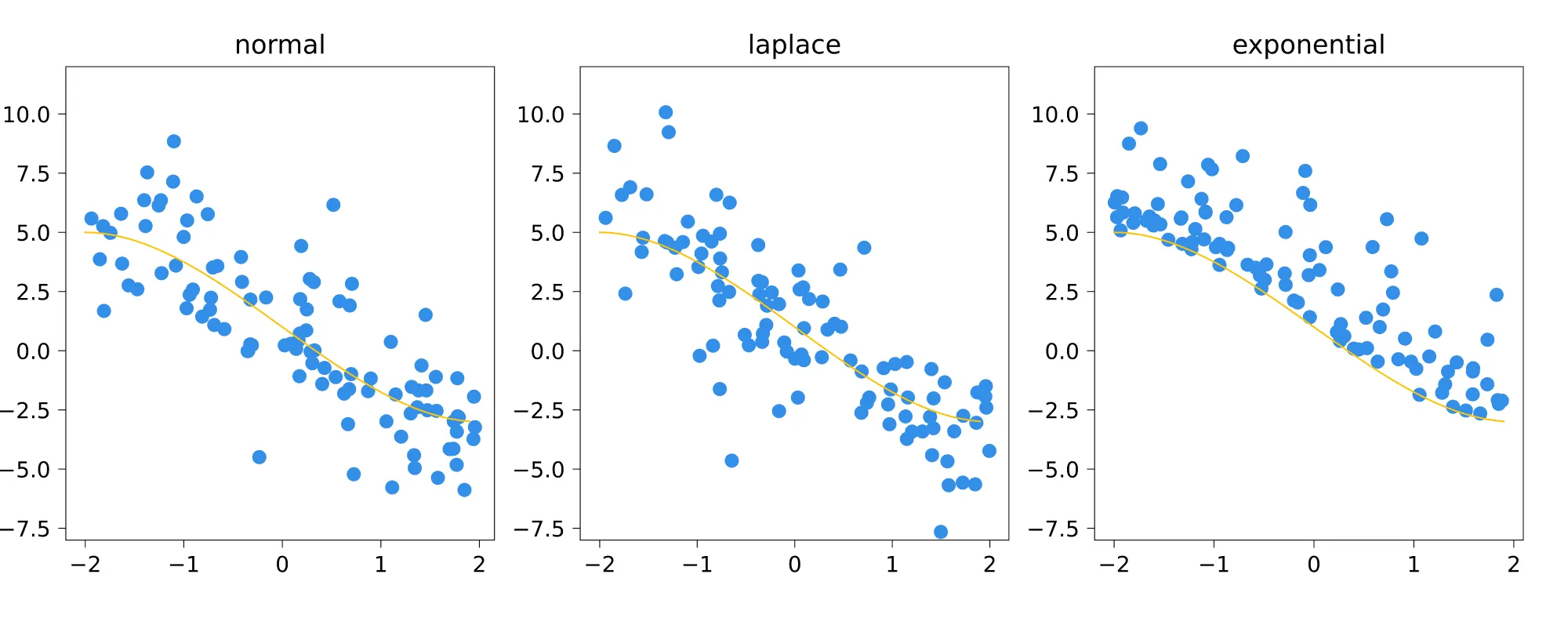
Условное распределение на таргет, дискретный случайУсловное распределение на таргет, дискретный случай

Допустим, мы имеем дело с задачей классификации с классами. Как мы можем её решать? Самый наивный вариант — научиться по каждому объекту предсказывать некоторое число для каждого класса, и у кого число больше — тот класс и выбираем! Наверное, так можно сделать, если мы придумаем хорошую функцию потерь. Но сразу в голову приходит мысль: почему бы не начать предсказывать не просто число, а вероятность?

Таким образом, задача классификации сводится к предсказанию

и как будто бы выбору класса с наибольшей вероятностью. Впрочем, как мы увидим дальше, всё не всегда работает так просто.

Одну такую модель — правда, только для бинарной классификации — вы уже знаете. Это логистическая регрессия:

которую также можно записать в виде

где — распределение Бернулли с параметром .

Нахождение вероятностей классов можно разделить на два этапа:

где, напомним, — это сигмоида:

Сигмоида тут не просто так. Она обладает теми счастливыми свойствами, что

• монотонно возрастает;

• отображает всю числовую прямую на интервал ;

• .

Вот такой вид имеет её график:

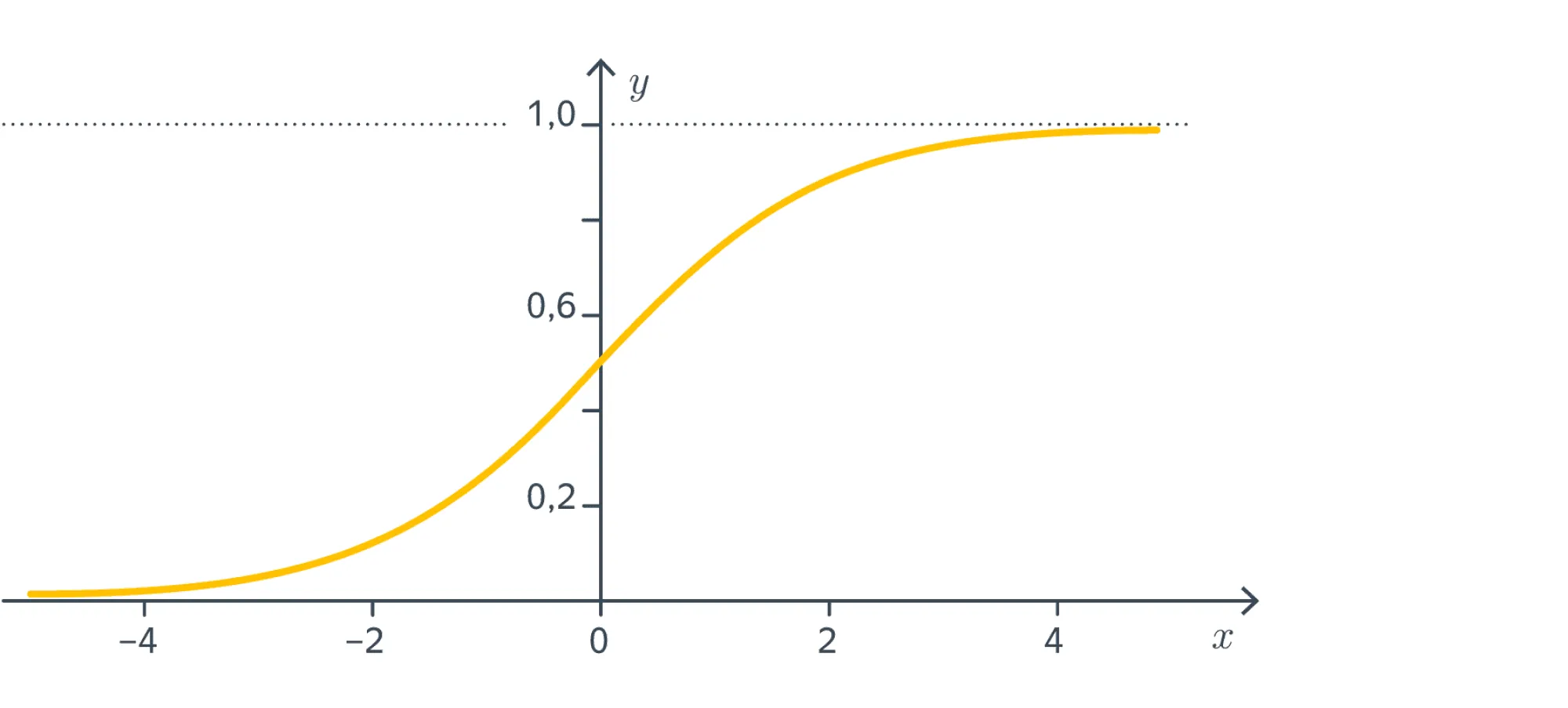
Иными словами, с помощью сигмоиды можно делать «вероятности» из чего угодно, то есть более или менее для любого отображения (из признакового пространства в ) с параметрами построить модель бинарной классификации:

Как и в случае логистической регрессии, такая модель равносильна утверждению о том, что

Похожим способом можно строить и модели для многоклассовой классификации. В этом нам поможет обобщение сигмоиды, которое называется softmax:

А именно, для любого отображения из пространства признаков в мы можем взять модель

Если все наши признаки — вещественные числа, а — просто линейное отображение, то мы получаем однослойную нейронную сеть

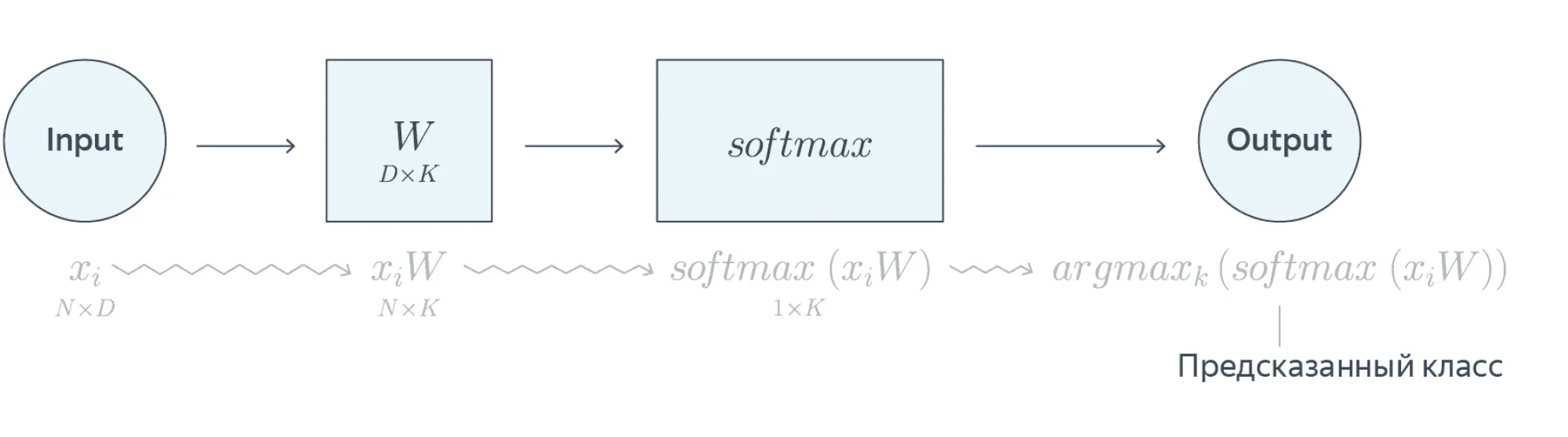
Предостережение. Всё то, что мы описали выше, вполне работает на практике (собственно, классификационные нейросети зачастую так и устроены), но корректным не является.

В самом деле, мы говорим, что строим оценки вероятностей , но для подбора параметров используем не эмпирические вероятности, а только лишь значения , то есть метки предсказываемых классов. Таким образом, при обучении мы не будем различать следующие две ситуации:

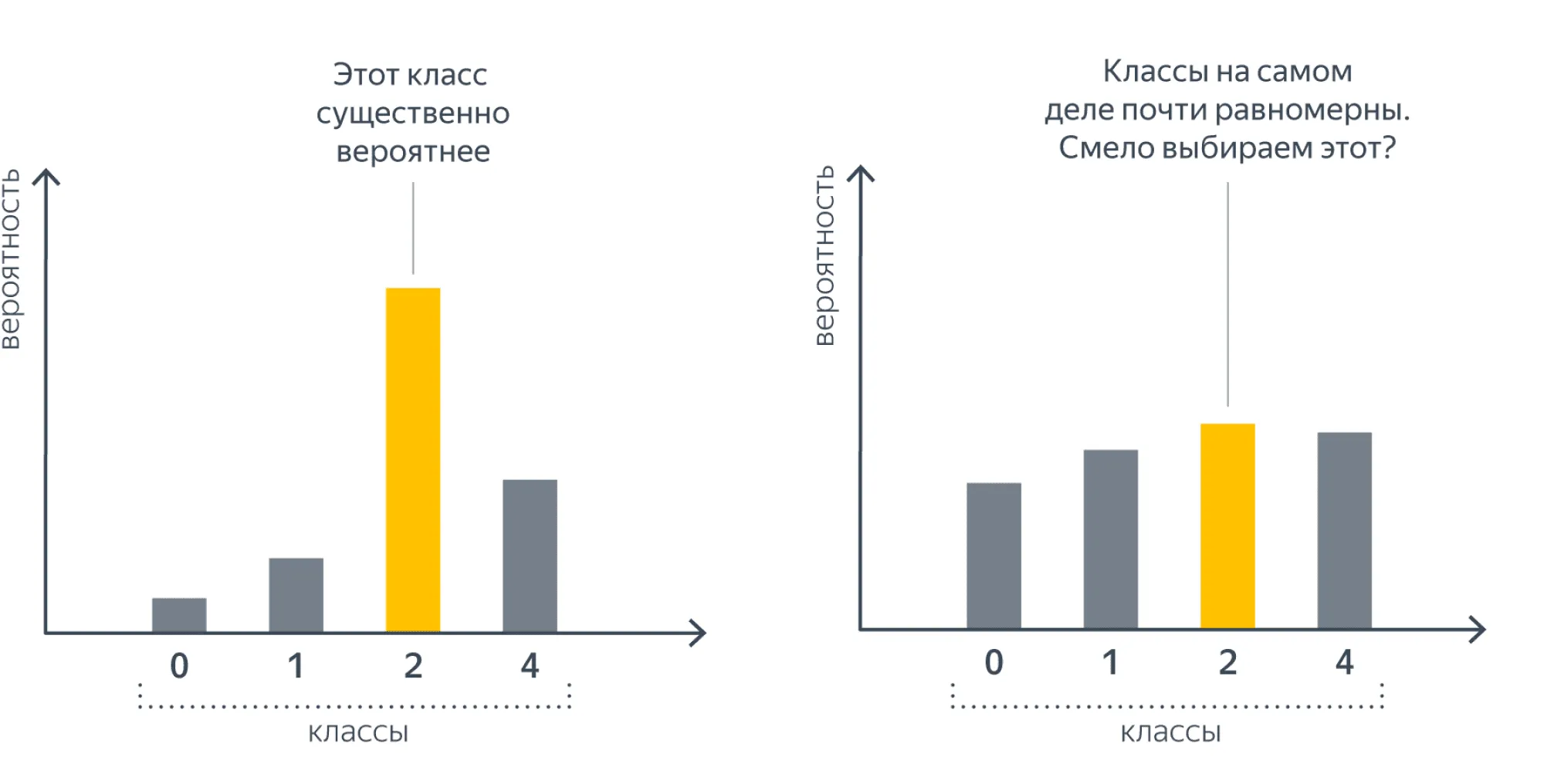
Это говорит нам о некоторой неполноценности такого подхода.

Заметим ещё вот что. В случае бинарной классификации выбор предсказываемого класса как равносилен выбору того класса, для которого . Но если наши оценки вероятностей неадекватны, то этот вариант проваливается, и мы встаём перед проблемой выбора порога: каким должно быть значение , чтобы мы могли приписать класс 1 тем объектам , для которых ?

В одном из следующих параграфов мы обсудим, как всё-таки правильно предсказывать вероятности.