В машинном обучении есть довольно широкая область, посвящённая обучению генеративных моделей. Их задача — выучить распределение, из которого могли бы быть насемплированы объекты обучающей выборки.
Обученная генеративная модель способна семплировать из выученного распределения новые объекты, не принадлежащие исходным данным. Чаще всего это связано с задачей генерации новых изображений: от изображений рукописных чисел до замены лиц на видео с помощью deepfake.
Модель, о которой пойдёт речь в данном параграфе, называется «Вариационный автоэнкодер» или VAE (variational autoencoder). Она относится к семейству генеративных моделей. Коротко расскажем, что вас ждёт дальше.
- В разделах «Постановка задачи» и «Обучение VAE» мы опишем построение и обучение VAE в классическом описании. Этих двух разделов достаточно для общего представления о VAE.
- Раздел «Обзор статей» для первоначального понимания не обязателен, но может быть интересен тем, кто захочет узнать о недавних интересных работах, связанных с VAE.
Прежде чем двинуться дальше — небольшое напоминание: большинство картинок в тексте кликабельны, и при клике вы сможете перейти к источнику, из которого была заимствована картинка.
Постановка задачи
Давайте представим себе, что нам нужно нарисовать лошадь. Как бы мы это сделали?
Наверное, сначала наметили бы общий силуэт лошади, её размер и позу, а затем стали бы добавлять детали: гриву, хвост, копыта, выбирать окраску шерсти и так далее. Кажется, что в процессе обучения рисованию мы учимся выделять для себя основной набор каких-то факторов, наиболее важных для генерации нового изображения: общий силуэт, размер, цвет и тому подобное, а во время рисования уже просто подставляем какие-то значения факторов.
При этом одинаковые сочетания одних и тех же факторов могут привести к разным картинкам — ведь нарисовать что-то два раза абсолютно одинаково вы, скорее всего, не сможете.
Попробуем формализовать описанный выше процесс. Пусть у нас есть датасет в многомерном пространстве исходных данных , — объектов, которые мы желаем генерировать, — и пространство скрытых (латентных) переменных меньшей размерности, которыми кодируются скрытые факторы в данных. Тогда генеративный процесс состоит из двух последовательных стадий (см. картинку ниже):
- Семплирование из распределения (красное)
- Семплирование из распределения (синее)
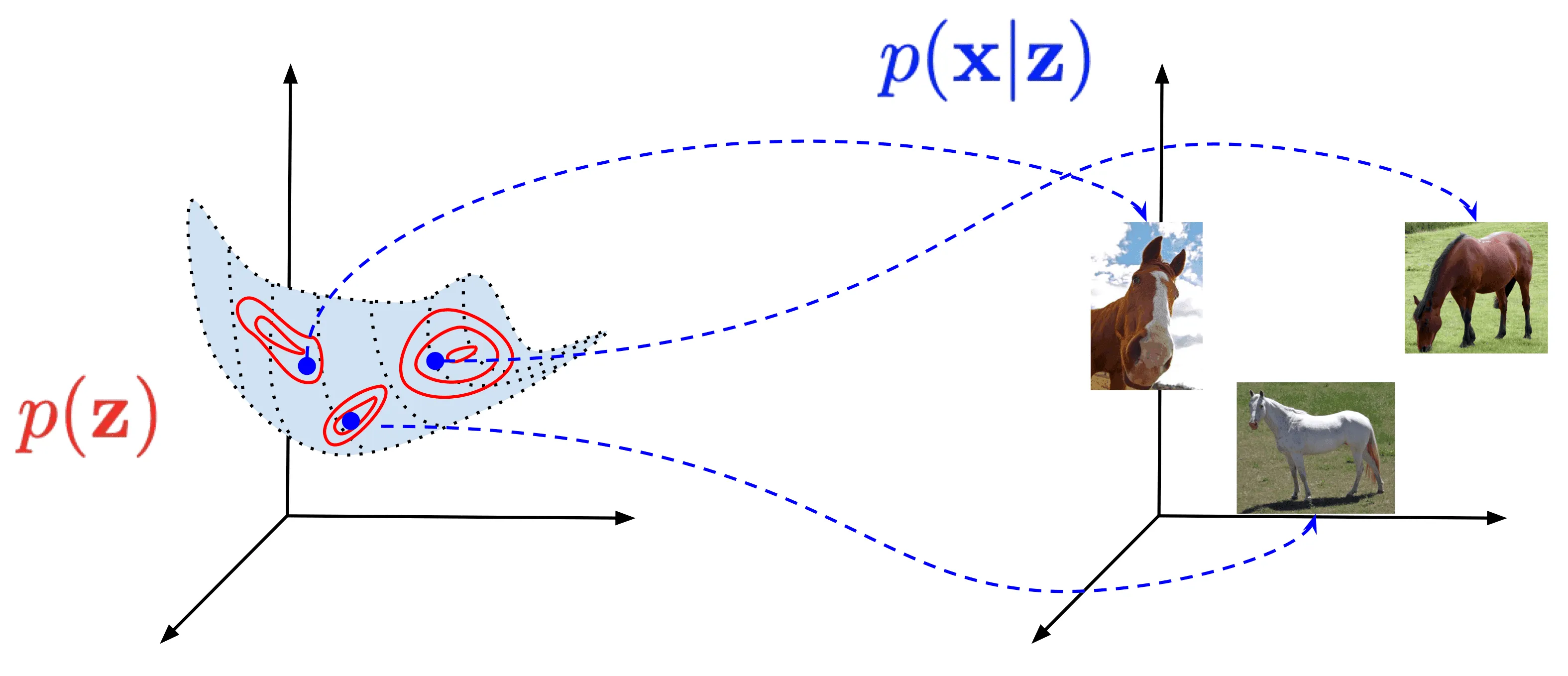
То есть, рассуждая в терминах рисования картинок с лошадками, мы сначала мысленно семплируем некоторое (размер, форму, цвет, ...), затем дорисовываем все необходимые детали, то есть семплируем из распределения , и в итоге надеемся, что получившееся будет напоминать лошадку.
Таким образом, построить генеративную модель в нашем случае — значит уметь семплировать с помощью описанного двустадийного процесса объекты, близкие к объектам из обучающей выборки .
Говоря более формально, нам бы хотелось, чтобы наша модель максимизировала правдоподобие элементов обучающего множества при описанной процедуре генерации:
Предположим, что совместное распределение параметризовано некоторым параметром и выражается непрерывной по функцией при каждых фиксированных и :
Тогда
и мы можем записать следующую задачу оптимизации:
Решив её, мы построим нашу генеративную модель.
Замечание 1. После приведённой выше аналогии с обучением рисованию может ошибочно показаться, что в скрытые переменные всегда заложен некоторый хорошо интерпретируемый смысл. Но на практике это всё же не обязано быть так: те скрытые переменные, которые мы найдём, могут как иметь простую интерпретацию, так и не иметь. С помощью объяснений выше мы прежде всего хотели проиллюстрировать понятие «скрытые переменные».
Замечание 2. Может показаться, что нам откуда-то уже известно, и тогда не ясно, зачем все эти сложности с введением латентных переменных и интегралами. На самом деле, мы действительно можем построить статистическую оценку по данным и даже пытаться генерировать новые данные с помощью таких моделей (как, например, делается тут). Но у статистических методов есть разные ограничения, наиболее серьёзным из которых представляется проклятие размерности: чем больше измерений у ваших данных, тем больше разнообразных примеров вам нужно для построения адекватной оценки . О проклятии размерности мы поговорим чуть подробнее далее.
Замечание 3. Также может возникать вопрос — а зачем вообще нужно вводить латентные переменные, моделировать совместное распределение , а целевое распределение определять как маргинализацию по ? Почему такой подход в принципе должен работать? Ответ состоит в том, что, даже имея относительно простые выражения для и , можно описать достаточно сложное распределение , что достаточно наглядно проиллюстрировано в примере ниже.
Пример: смесь гауссиан
Представьте себе, что у вас есть таблица с конечным числом строк, в -й строке которой записано два числа — среднее и дисперсия нормального распределения. Пусть на индексах строк этой таблицы определено дискретное распределение , такое что:
Пусть мы насемплировали индекс , взяли параметры распределения из соответствующей ему строки и насемплировали с этими параметрами объект . Распределение, из которого был получен , равно:
Распределение получается маргинализацией совместного распределения по :
Получилось, что описывается смесью гауссиан и имеет более сложный вид, чем и :
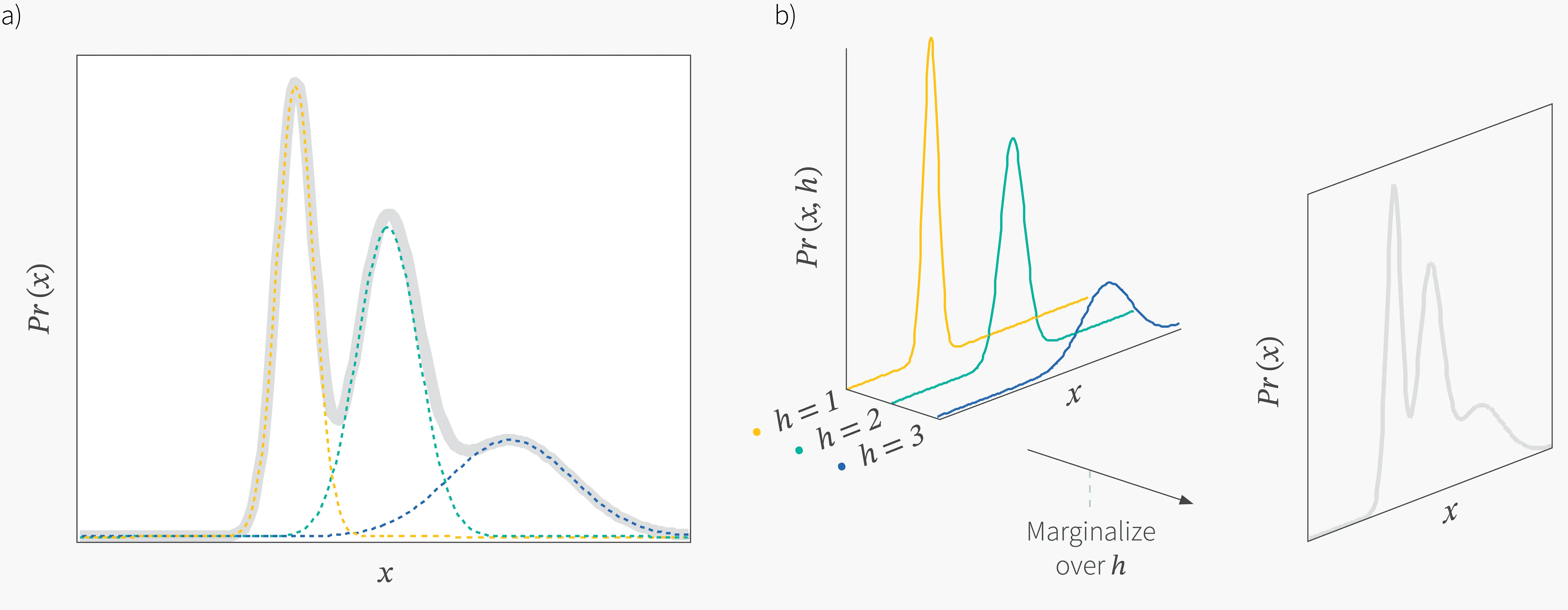
Ясно, что чем больше гауссиан в нашей сумме, тем более сложную форму может иметь . Так, имея простые и , мы можем моделировать сложные мультимодальные распределения. А теперь представим себе, что априорное распределение имеет уже не дискретные, а непрерывные значения. Рассмотрим, например, такой случай:
Распределение , аналогично случаю с дискретным априорным распределением, будет получено интегрированием по и будет как бы «бесконечной» смесью гауссиан:
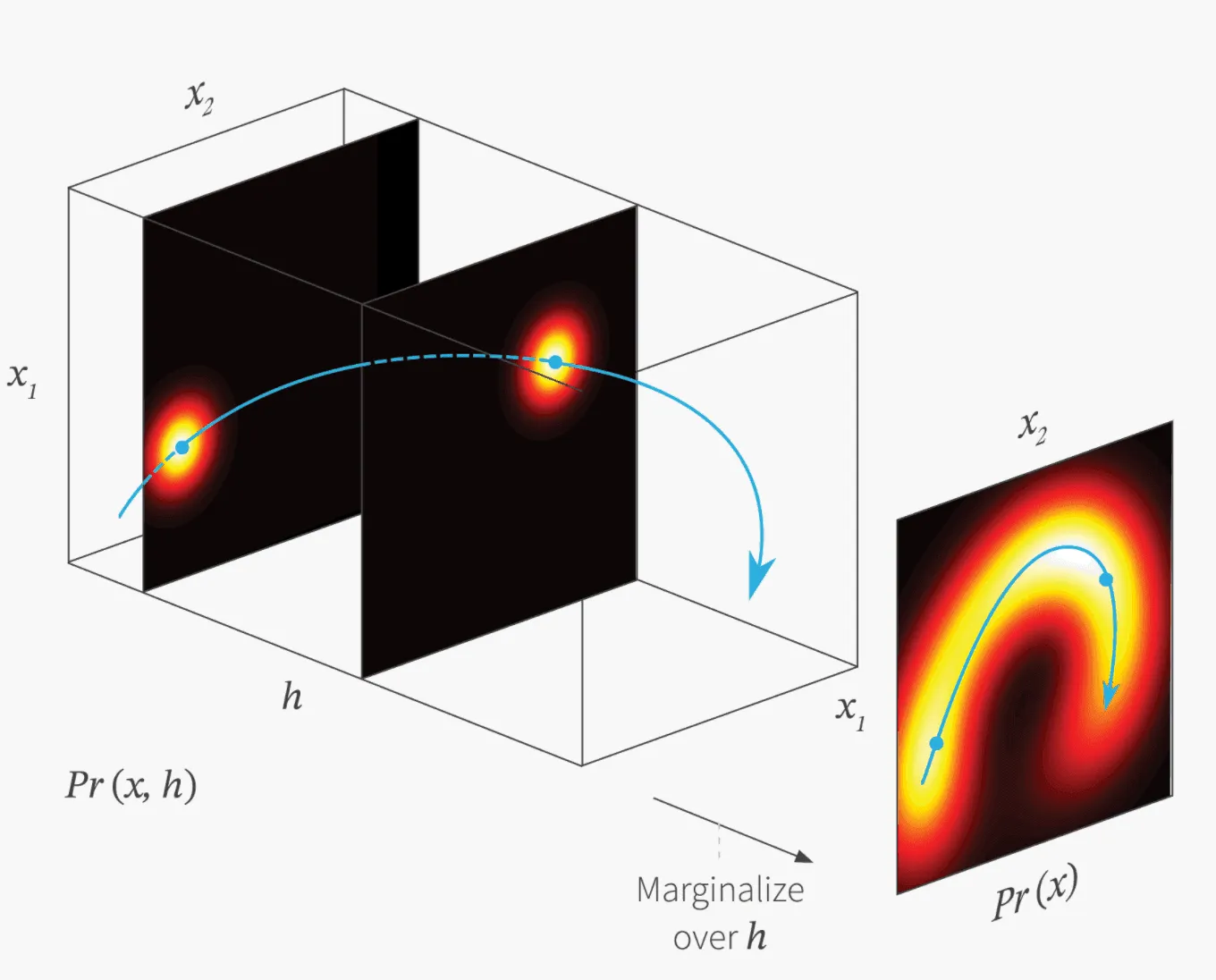
С этим разобрались. В следующей главе продолжим говорить о задаче оптимизации, о которой мы начали разговор чуть выше — не теряйтесь!
Обучение VAE
Прежде чем пытаться решать задачу оптимизации $ (1) $, давайте подумаем, а как мы вообще могли бы посчитать такой интеграл? Первое, что приходит на ум, — попробовать получить его приближённое значение методом Монте-Карло:
где в последнем переходе мы используем сэмплы . Однако, если и — достаточно большое, мы столкнёмся с проклятием размерности — количество семплов, необходимых для того, чтобы хорошо покрыть , растёт экспоненциально с ростом :
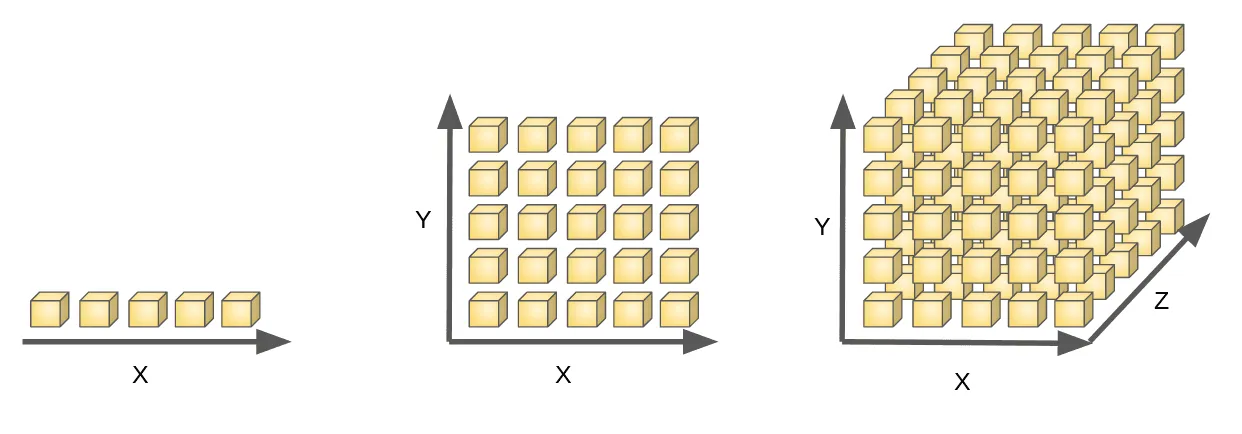
Есть ли способ как-то сократить число необходимых семплов для подсчёта $ (1) $? На самом деле, часто оказывается, что далеко не все возможные отображаются в элементы , и вклад большинства в оценку практически нулевой. Это наводит на мысль, что для каждого нам может пригодиться знание распределения таких , которые являются прообразами . Мы можем предположить, что распределение параметризовано некоторым семейством параметров :
Зная распределение , мы могли бы семлировать уже только из него, а не из всего , и, если распределение окажется достаточно хорошим, число необходимых семплов значительно сократится.
О том, как построить , мы поговорим позже. Сейчас стоит обратить внимание на то, что процессы семплирования из распределений и взаимно обратны друг к другу: первое отображает элементы датасета в подмножество латентного пространства , то есть действует как энкодер, а второе отображает латентные переменные в подмножество , то есть действует как декодер:
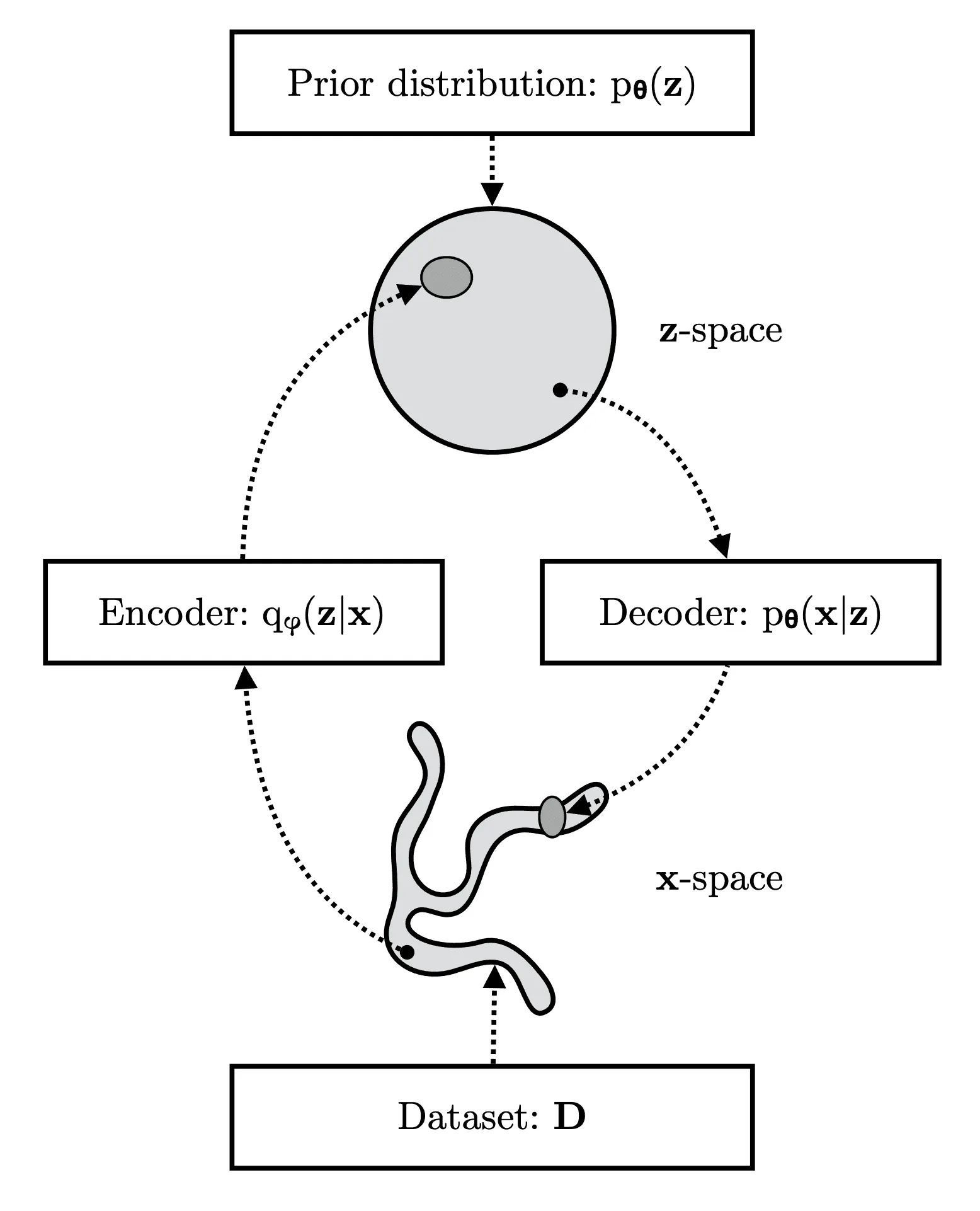
Так как оба эти распределения будут участвовать в обучении VAE, возникает аналогия между VAE и моделями-автоэнкодерами, имеющими похожую структуру.
Вывод функции потерь
Сейчас у нас всё готово для того, чтобы записать общий вид функции потерь для обучения вариационного автоэнкодера. Напомним, что мы обучаем модель путём максимизации правдоподобия по . Для удобства мы перейдём к логарифму правдоподобия:
Оптимизировать напрямую это выражение тяжело из-за проклятия размерности, обсуждавшегося в прошлом разделе. Чтобы победить проклятие размерности, мы хотели бы заменить семплирование из априорного распределения на семплирование из , для чего придётся осуществить некоторый трюк. Для любого , отличного от нуля для всех , мы можем выписать следующую цепочку равенств:
Второе слагаемое в последнем равенстве — -дивергенция между и , которая, как известно, неотрицательна:
А первое слагаемое — это величина, именуемая в английской литературе evidence lower bound (ELBO):
Первое слагаемое в последнем переходе обычно называют reconstruction loss, так как оно оценивает качество восстановления декодером объекта из его латентного представления . А второе играет роль регуляризационного члена и подталкивает распределение, генерируемое энкодером, быть ближе к априорному распределению.
Так как -дивергенция неотрицательна, ELBO является нижней границей для логарифма правдоподобия данных:
Посмотрим повнимательнее на равенства, которые мы выписали.
- Функцию можно оптимизировать градиентным спуском (SGD), предварительно выбрав удобный вид для , и $ p_\theta (z)$. Максимизируя , мы растим , тем самым улучшая нашу генеративную модель. Оптимизацию ELBO с помощью SGD мы будем подробно обсуждать в следующем разделе.
- Максимизируя , мы одновременно минимизируем . Распределение оценивает, из каких мог бы быть сгенерирован объект , и заранее оно нам не известно. Но если мы выберем достаточно большую модель для , то в процессе оптимизации может очень сильно приблизиться к , и тогда мы будем напрямую оптимизировать . Заодно мы получаем приятный бонус: для оценки распределения прообразов мы сможем использовать вместо невычислимого . То есть , которое мы при выводе формулы ввели в рассмотрение как произвольное распределение, действительно будет играть роль энкодера для модели.
Альтернативный вывод выражения для ELBO
В рассуждениях выше введение в рассмотрение могло показаться довольно формальным. Поэтому мы приведём здесь ещё один подход к выводу выражения для ELBO, который может показаться более естественным. Он состоит в последовательном применении приёма, называемого importance sampling, и неравенства Йенсена.
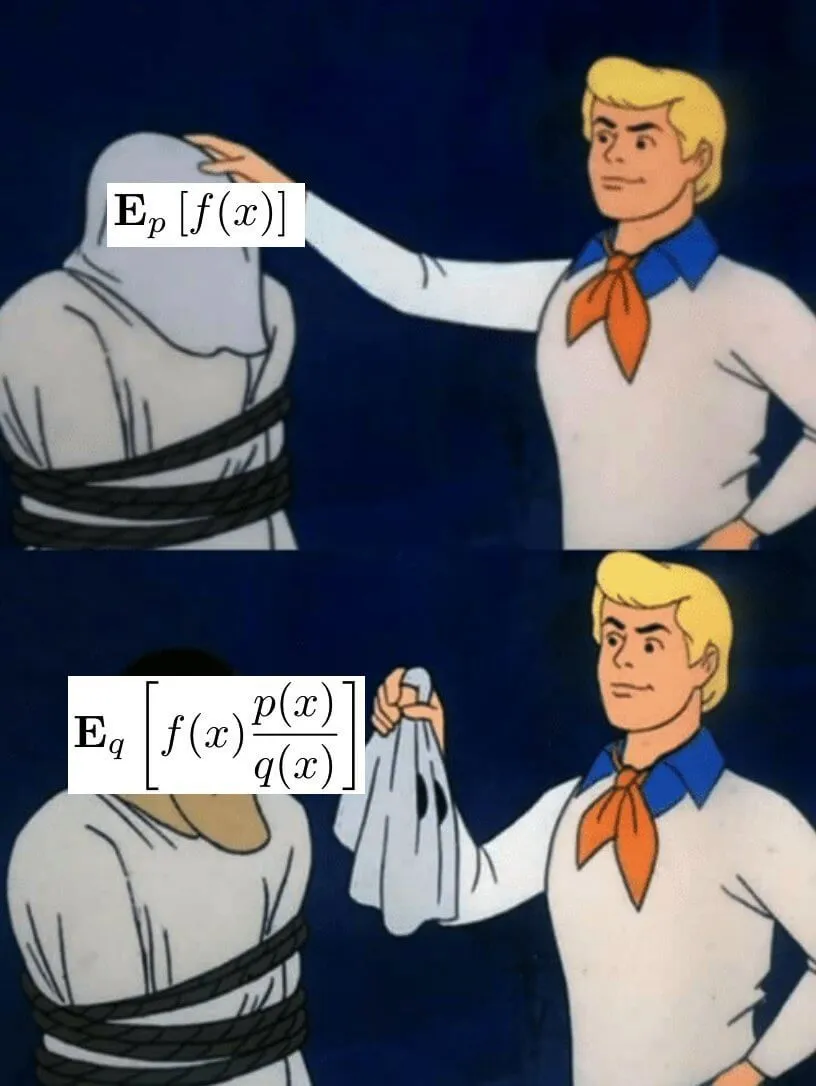
Во многих практических задачах возникает ситуация, в которой мы хотим вычислить , но при этом близка к нулю вне некоторой области , а вероятность попасть в эту важную область очень мала: .
Множество может либо иметь слишком маленькую мощность, либо быть в хвосте распределения случайной величины . Обычное семплирование по методу Монте-Карло может почти не сгенерировать примеров, которые бы попадали в множество . Проблемы такого типа довольно часто встречаются в физике высоких энергий, байесовском выводе, прогнозировании опасных природных явлений и во многих других областях.
Достаточно интуитивным выглядит решение, состоящие в том, чтобы попробовать как-то искусственно увеличить долю важных примеров среди всех остальных. Это можно сделать, используя распределение, дающее больше веса примерам из важной области. Отсюда и название метода — importance sampling (выборка по значимости).
Итак, пусть наша задача — вычислить математическое ожидание , где
- — плотность распределения на множестве ,
- — некоторая интегрируемая функция.
Пусть — функция плотности вероятности, определённая и положительная на , позволяющая осуществлять семплирование примеров из некоторого интересующего нас узкого подмножества. Наша задача — перейти от семплирования из к семплированию из для оценки . Поскольку среднее , вообще говоря, не равно , запишем следующее:
Исходная плотность называется номинальной (nominal distribution), а плотность — смещённой (importance distribution). Отношение правдоподобия компенсирует смещение, возникающее при переходе от к .
Напомним также формулировку неравенства Йенсена для случайных величин.
Напомним также формулировку неравенства Йенсена для случайных величин: если — случайная величина с конечным математическим ожиданием и — выпуклая функция, то:
Теперь вернёмся к исходной задаче. Снова, для любого , отличного от нуля для всех , мы можем записать:
В результате проведённых выкладок мы, как можно заметить, снова получили выражение для ELBO. На третьем переходе мы применили importance sampling, а на четвёртом — неравенство Йенсена для .
Минус данного подхода состоит в том, что он, в отличие от предыдущего способа, не позволяет выписать в явном виде формулу для разности между и ELBO:
Но зато данный вывод естественным образом следует из более общих методов, не требуя применения искусственных трюков.
Обучение VAE с помощью градиентного спуска
Важное свойство ELBO в том, что его можно оптимизировать градиентным спуском относительно параметров и . Если объекты датасета независимы и одинаково распределены, то запишется как сумма (или среднее) значений на объектах :
Значения и их градиенты в общем случае вычислить невозможно, однако можно получить их несмещённые оценки, что позволит нам использовать стохастический градиентный спуск.
Оценку для градиента по параметрам получить несложно:
где в последней строчке . Однако оценку на градиент по параметрам получить сложнее, ведь они также участвуют и в семплировании:
В общем случае эта проблема не разрешима. Однако некоторые распределения позволяют применить репараметризацию (reparameterization trick): представить переменную как обратимую дифференцируемую функцию от случайного шума, параметров и переменнной :
Здесь распределение не зависит от и . Например, пусть . Тогда может иметь следующий вид:
После такой замены мы сможем получить оценку на градиент по :
где в последней строчке . Репараметризация хорошо иллюстрируется следующей картинкой:
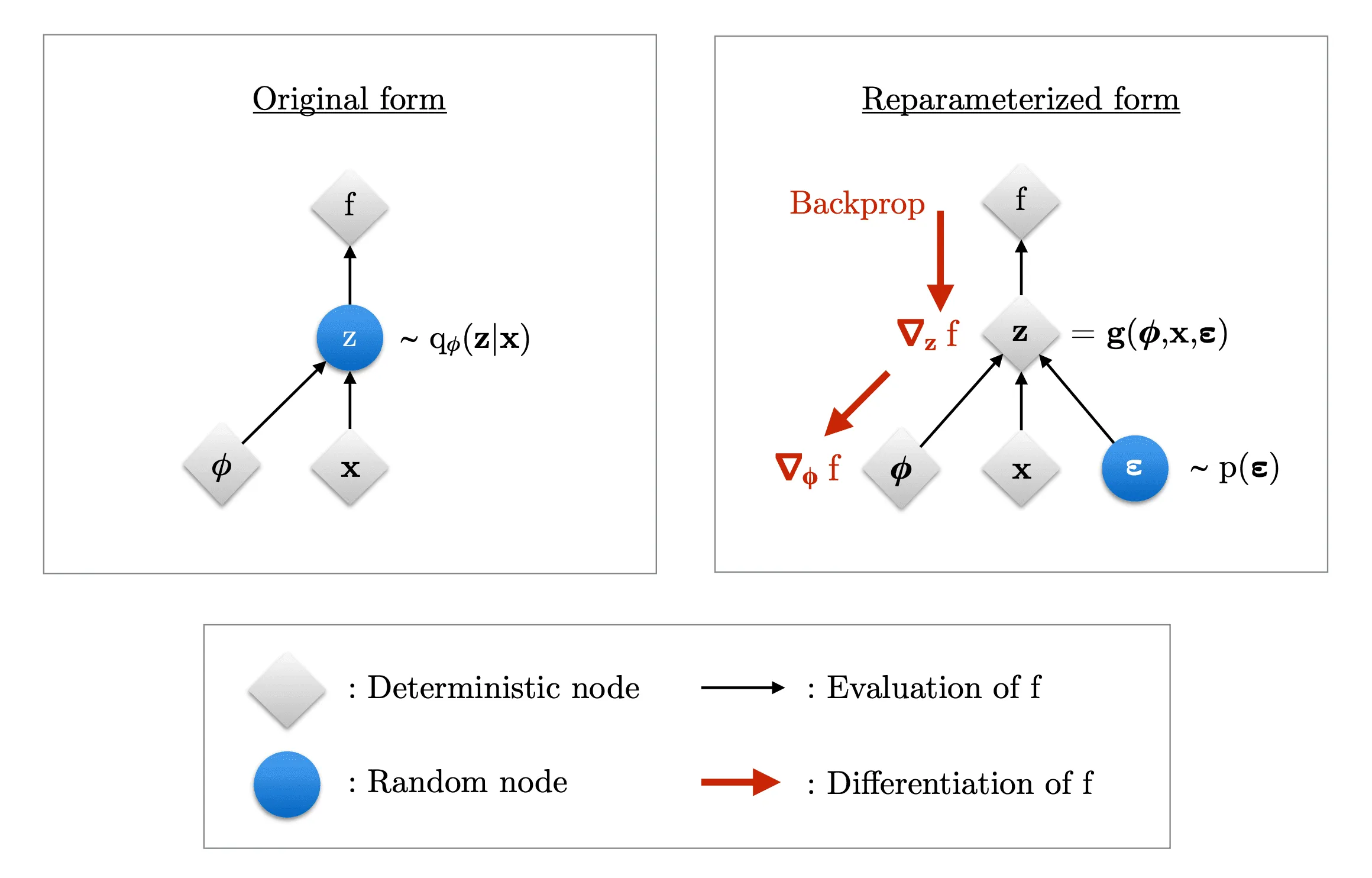
Здесь — функция потерь. Значения на обеих схемах одинаковы, но на левой картинке градиенты по рассчитать не получится, так как мы не можем дифференцировать по случайной переменной .
Однако на правой картинке источник случайности перемещается во входные данные благодаря репараметризации, а градиенты вычисляются по детерминированным переменным. Таким образом, мы получили сетап, типичный для оптимизации с помощью SGD: там мы приближаем градиент функции потерь по случайным батчам входных данных, а здесь роль случайных батчей играют одновременно батчи из переменных и случайных переменных .
Кроме нормального распределения, есть довольного много примеров распределений, допускающих репараметризацию. Их можно найти по ссылке в разделе "The reparameterization trick". Однако большая часть реализаций VAE используют именно нормальное распределение.
В итоге примерный алгоритм обучения VAE такой:
dataset = np.array(...)
epsilon = RandomDistribution(...)
# Энкодер q_phi(z|x) — нейронная сеть с параметрами phi
encoder = Encoder()
# Декодер p_theta(x|z) — нейронная сеть с параметрами theta
decoder = Decoder()
for step in range(max_steps):
# Семплируем батч исходных данных и случайного шума
batch_x = sample_batch(dataset)
batch_noise = sample_batch(epsilon)
# Считаем параметры распределения q(z | x) с помощью энкодера
latent_distribution_parameters = encoder(batch_x)
# Делаем репараметризацию (семплируем из q(z | x))
z = reparameterize(latent_distribution_parameters, batch_noise)
# Декодер отдаёт параметры выходного распределения
output_distribution_parameters = decoder(z)
# Вычисляем ELBO и обновляем параметры моделей
L = -ELBO(
latent_distribution_parameters,
output_distribution_parameters,
batch_x
)
L.backward()
Стоит подчеркнуть, что декодер выдаёт именно параметры выходного распределения, а не конкретный семпл из этого распределения. Например, если вы моделируете выходные изображения с помощью нормального распределения , то декодер на выходе предскажет некоторые и , которые вместе с параметрами латентного распределения (выход энкодера) будут поданы в ELBO.
Для генерации конкретной картинки на этапе инференса нужно будет либо честно провести семплирование из , либо, как часто делают, просто взять среднее в качестве выходного изображения. В общем случае конкретный способ проведения инференса зависит от вида используемого выходного распределения.
Выбор вида используемых распределений
Пришло время привести примеры конкретных , и , с которыми можно построить VAE. Для начала предположим, что можно положить равным стандартному нормальному распределению:
Заметим, что в этом случае у априорного распределения отсутствует зависимость от параметров .
Распределение зависит от того, к какому распределению принадлежат ваши данные. Если ваши данные имеют непрерывное распределение, то можно задать, например, как гауссовское распределение:
Вектор средних в этом примере определяется функцией с переменными и , а матрица ковариаций определяется постоянной диагональной матрицей. Функцию можно задать с помощью нейронной сети с параметрами . При желании, матрицу ковариаций тоже можно задавать некоторой функцией и не ограничивать её вид только постоянными матрицами. Если же ваши данные дискретны, то может подойти категориальное распределение:
в котором вектор вероятностей — выход нейросети после применения . Если у вас бинарные данные, вы можете использовать бернуллиевское распределение:
где — выход нейронной сети после применения сигмоиды.
Распределение может, в принципе, быть любым, но в самом простом случае оно имеет вид гауссовского распределения c диагональной матрицей ковариаций:
Такое распределение позволяет, в частности, применить репараметризацию, обсуждавшуюся выше. Если выбрать двумерным, то распределения, определямые , хорошо визуализируются:
А теперь вспомним, как определяется ELBO:
Вычислим его для приведённых выше распределений.
Начнём с . -дивергенция между распределениями и равна:
где — размерность этих распределений. Вывод этого соотношения можно найти здесь. В нашем случае , и
Тогда ELBO будет вычисляться как:
где . Как было упомянуто в этой статье от авторов VAE в разделе 2.3, число семплирований можно положить равным единице при достаточно большом размере батча (например, 100).
Если вы выберете биномиальное , то
Если гауссовское , то
Пример реализации обучения и применения VAE на датасете MNIST на Keras можно найти здесь, а на PyTorch — здесь.
Инференс обученной модели
Когда мы обучили VAE, мы сможем генерировать новые семплы, просто подавая на вход декодеру:
![2](https://yastatic.net/s3/education-portal/media/vae_decoder_diagram_385be2e566_6c396a28e8.svg">
Энкодер для генерации новых семплов не нужен. Однако нам может понадобиться оценить для из тестового множества, чтобы понять, с какой вероятностью модель сможет сгенерировать . Для оценки интеграла нам нужно насемплировать некоторое количество , и если брать семплы из , то оценка может плохо сойтись. Но можно снова использовать ELBO как нижнюю границу для и оценивать уже её, семплируя из распределения . Такая оценка сойдётся быстрее и даст примерное представление о том, насколько хорошо модель справляется с конкретным примером .
Также интересно бывает взглянуть на то, как распределены коды обучающих примеров в латентном пространстве. Так, например, может выглядеть распределение латентных кодов цифр MNIST для обученного VAE в двумерном латентном пространстве:
Разные типы цифр обозначены разными цветами (соответствие цифр и цветов показано на шкале сбоку). Здесь видно, что лучше всего модель различает нули и единицы, а восьмёрки и тройки — хуже всего. Стоит, конечно, отметить, что латентное пространство выбрано двумерным в целях визуализации, и при большей его размерности модель могла бы научиться различать цифры более качественно.
Для двумерного латентного пространства есть ещё один интересный способ визуализировать структуру многообразия, выученного VAE. Можно взять равномерную сетку на единичном квадрате и отобразить её в латентное пространство, применив к ней функцию, обратную к CDF нормального распределения.
Почему это сработает
Узлы равномерной сетки можно в некотором приближении считать семплами из равномерного распределения: . Поэтому семплы приближённо подчиняются нормальному распределению:
Полученные семплы можно подать в декодер и посмотреть, какие картинки будут соответствовать узлам сетки:
Здесь изображены примеры, сгенерированные для датасетов Frey Face и MNIST (оба доступны по ссылке). Такая визуализация позволяет увидеть плавный переход латентных кодов одних объектов в коды других, а также взаимное расположение латентных кодов.
Для MNIST снова видно, в частности, что коды нулей и единиц модель разнесла далеко друг от друга, а коды троек и восьмёрок очень близки. А ещё интересно наблюдать плавный переход от шестёрок к нулям и от семёрок к единицам. Для Frey Face видно, что весёлые лица расположены далеко от грустных, а по главной диагонали квадрата можно проследить плавный переход от серьёзного лица к улыбающемуся.
Ещё интересно посмотреть на то, как меняется качество генерируемых цифр в зависимости от размерности латентного пространства (на картинках просто случайные семплы из модели):
Заметный переход виден между размерностями 2 и 5, дальнейший рост размерности почти не оказывает значимого эффекта.
Conditional VAE (CVAE)
Иногда мы можем захотеть сгенерировать не просто какой-то произвольный объект из датасета, а относящийся к конкретной группе или классу. Ранее мы выписывали уравнение для :
Все распределения, участвующие в этом уравнении, мы можем сделать обусловленными по переменной :
Переменная может быть лейблом объекта или вообще произвольным тензором, как-то характеризующим . Вместо , единого для всех из обучающей выборки, для каждого значения теперь будет отдельное априорное распределение .
Переменная может принимать и дискретные, и непрерывные значения. Она может даже, например, быть половиной изображения, которую модели предлагается дополнить. На всякий случай подчеркнём, что обучение CVAE — это не то же самое, что обучение нескольких независимых VAE, так как веса CVAE общие для всех классов.
На уровне имплементации это реализуется довольно просто: нужно всего лишь сконкатенировать входы энкодера и декодера с тензором, соответствующим . Если имеет категориальные значения, то бывает полезно предварительно закодировать их one-hot векторами. Алгоритм будет примерно таким:
dataset, labels = np.array(...), np.array(...)
epsilon = RandomDistribution(...)
# Энкодер q_phi(z|x) — нейронная сеть с параметрами phi
encoder = Encoder()
# Декодер p_theta(x|z) — нейронная сеть с параметрами theta
decoder = Decoder()
for step in range(max_steps):
# Семплируем батч исходных данных, лейблов и случайного шума
batch_x = sample_batch(dataset)
batch_y = sample_batch(labels)
batch_noise = sample_batch(epsilon)
# Подаём в энкодер конкатенацию входных данных и лейблов
encoder_input = concatenate([batch_x, batch_y])
# Считаем параметры распределения z с помощью энкодера
latent_distribution_parameters = encoder(encoder_input)
# Делаем репараметризацию
z = reparameterize(latent_distribution_parameters, batch_noise)
# Конкатенируем полученный случайный вектор и лейблы
decoder_input = concatenate([z, batch_y])
# Декодер отдаёт нам выходное изображение
output_distribution_parameters = decoder(decoder_input)
# Вычисляем ELBO и обновляем параметры
L = -ELBO(
latent_distribution_parameters,
output_distribution_parameters,
batch_x
)
L.backward()
Реализацию CVAE на PyTorch и Tensorflow можно найти, например, здесь.
Если визуализировать распределение латентных кодов для цифр MNIST, полученных после обуславливания модели на класс цифры, то можно увидеть что-то такое:
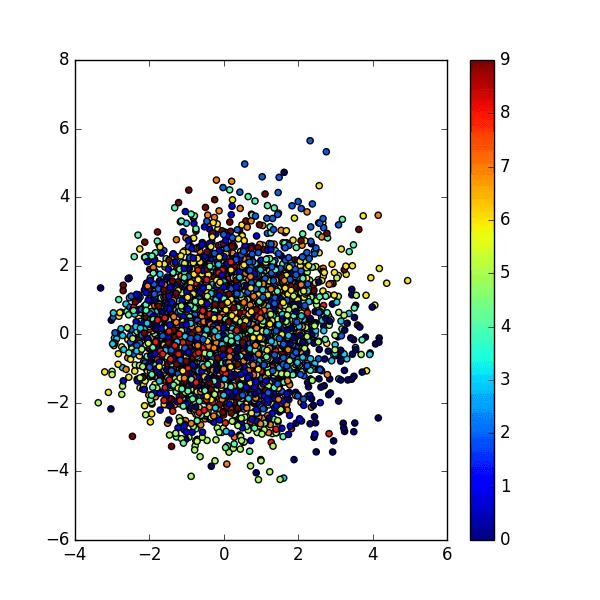
Мы видим непонятную смесь из точек вместо явных кластеров, которые выделяла обычная модель VAE. Однако дело тут в том, что, вместо того, чтобы пытаться размещать все цифры в одном пространстве , модель использует отдельное латентное пространство для каждой цифры:
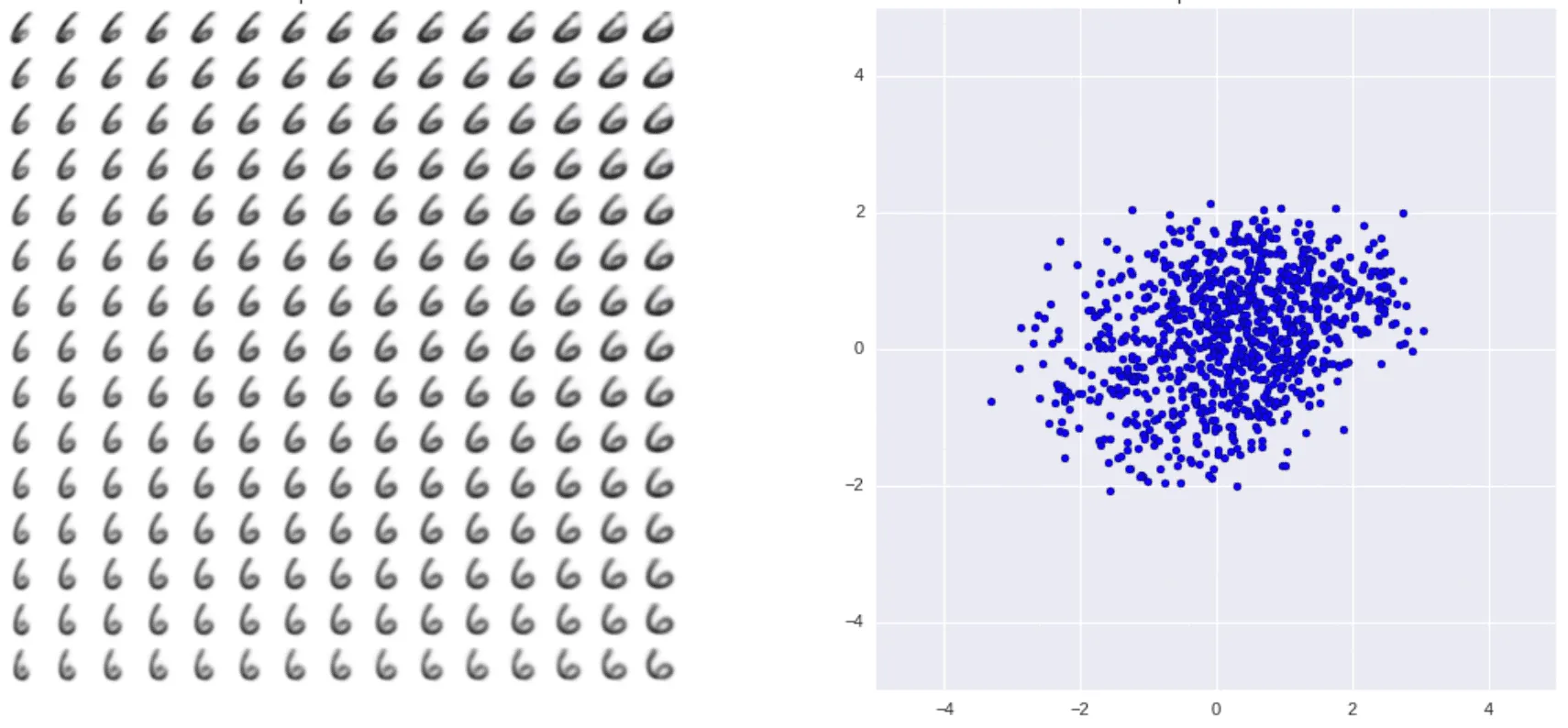
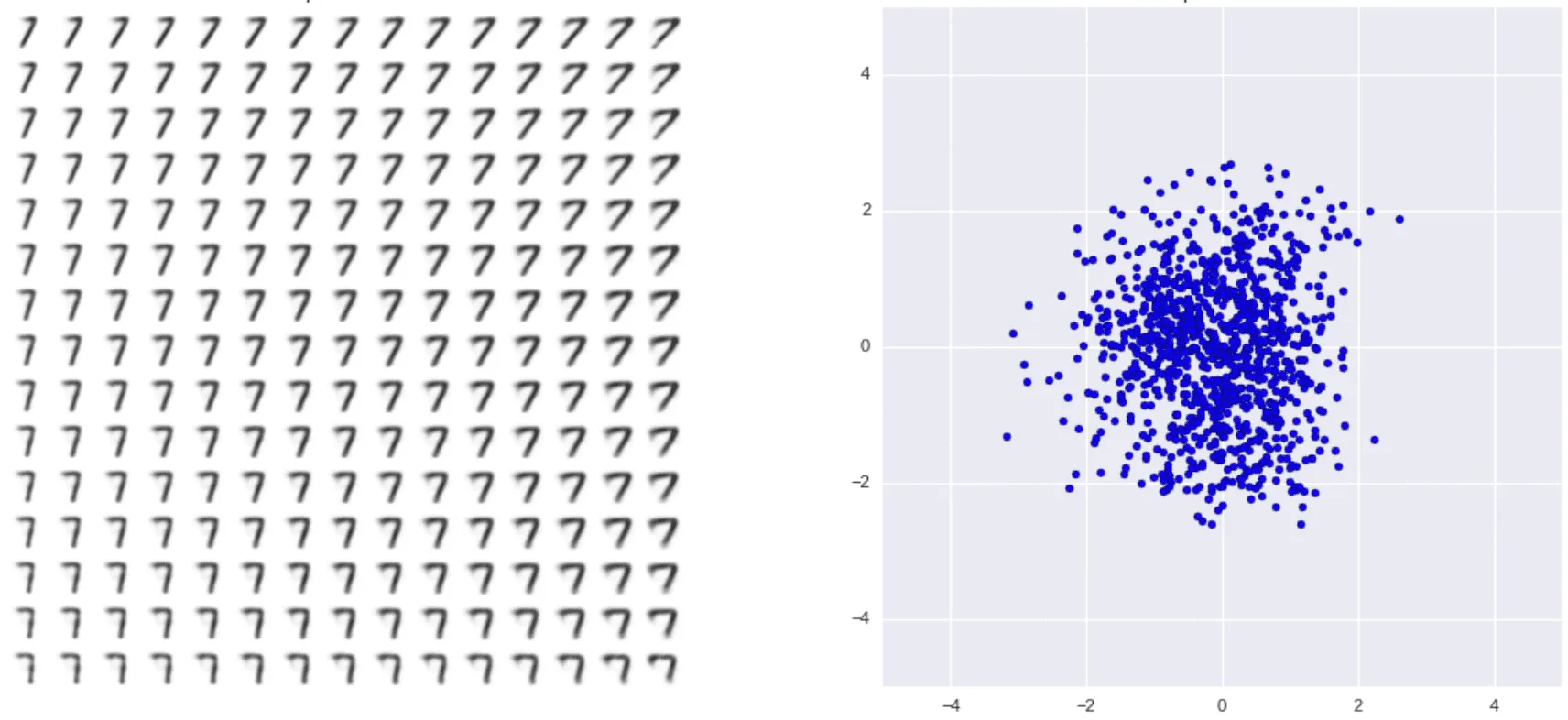
На картинке справа — априорные распределения для цифр 6 и 7, а слева — визуализация структуры выученных многообразий для этих цифр, построенная так же, как аналогичная визуализация для VAE. Качество изображений каждой отдельной цифры заметно повышается:
Видно, что вариабельность генерации цифр теперь тоже заметно выросла, и модель может имитировать написание цифр разными почерками.
Обзор статей
Кроме стандратного описания работы VAE, приведём результаты нескольких недавних интересных работ, базирующихся на идее VAE.
VQ-VAE и VQ-VAE-2
Модели VQ-VAE и VQ-VAE-2 интересны тем, что в них в качестве априорных распределений были задействованы дискретные распределения. В каких ситуациях дискретные распределения могут быть более применимы, чем непрерывные? Например, если мы имеем дело с токенам в задачах NLP или фонемами в обработке речи. Картинки также можно было бы кодировать некоторым набором из целых чисел: например, одно число могло бы кодировать тип объекта, другое — его цвет, третье — цвет фона и так далее:
Кроме того, существуют довольно мощные алгоритмы (например, Трансформер), предназначенные для работы с дискретными данными. Выучивание хороших дискретных представлений даёт возможность эффективно использовать такие алгоритмы для, например, задачи генерации картинок.
VQ-VAE
Авторы VQ-VAE вводят дискретное латентное пространство в виде вещественных векторов размерности . Векторы из этого пространства называются кодовыми векторами или кодами. На рисунке ниже приведена примерная схема обучения предлагаемой модели.
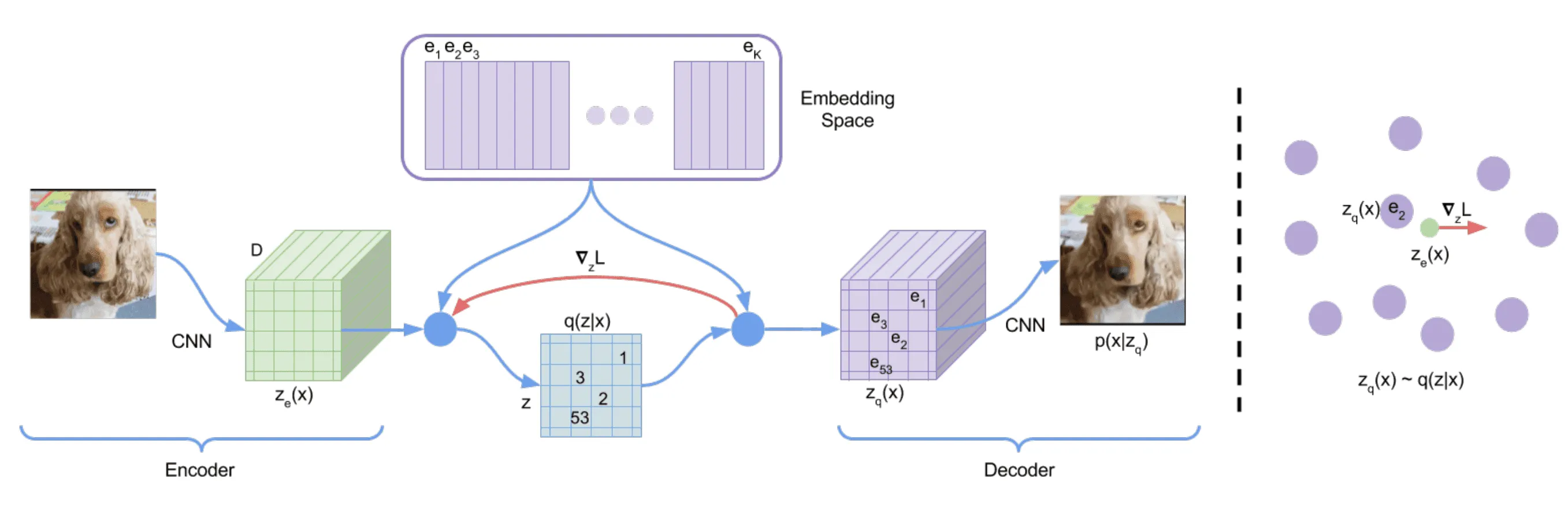
Энкодер принимает на вход картинку и выдаёт на выходе тензор . На рисунке этот тензор имеет размерность : последняя размерность совпадает с длиной кодовых векторов, а — это пространственная размерность выхода CNN (для простоты мы здесь не пишем явно размерность батчей).
Каждый из векторов из отображается в ближайший к нему по -расстоянию кодовый вектор. После такой процедуры тензор переходит в тензор , состоящий из кодовых векторов. Декодер получает на вход тензор и отображает его в исходную картинку. Для работы с речью и текстами авторы использовали двумерный тензор вместо трёхмерного.
Выходное распределение энкодера определено здесь следующим образом:
Во время обучения в качестве априорного распределения в латентном пространстве используется равномерное распределение , поэтому слагаемое оказывается постоянным и равным :
В точках, где , предпоследнее выражение продолжается нулём по непрерывности. Таким образом, ELBO для таких распределений примет вид
где — параметры декодера. При оптимизации можно не учитывать. Отображение выхода энкодера в кодовые векторы не дифференцируемо, поэтому при обучении применяется следующий трюк: при обратном проходе градиент копируется напрямую из декодера в энкодер, пропуская при этом слой, отображающий выходы энкодера в кодовые векторы.
Этот трюк очень близок к приёму, известному как straight-through estimator, впервые предложенному в этой статье (а его простое описание можно найти тут). Использование straight-through estimator, однако, не позволяет обучать сами кодовые векторы, так как по ним не будут вычисляться градиенты. Поэтому лосс для обучения модели складывается из трёх компонент:
Здесь обозначает оператор остановки дифференцирования: через его аргумент не текут градиенты.
В статье лосс записан несколько иначе:
Эти обозначения кажутся несколько путающими по двум причинам:
- Буква в нижнем индексе призвана обозначить только то, что это выход энкодера, а не наличие связи между кодовыми векторами и параметрами энкодера. Но второе довольно легко для себя предположить.
- Вычитание обозначает вычитание не всех элементов словаря из соответствующей позиции тензора , а только лишь ближайшего соседа к элементу на этой позиции. То есть по факту вычитание в этой записи равносильно вычитанию . Это не уточняется в статье, но можно увидеть в официальной реализации.
Первое слагаемое — это ELBO с точностью до константы. Второе слагаемое отвечает за сдвиг кодовых векторов в сторону выходов энкодера. Чтобы не получилось так, что выходы энкодера всё время меняют кодовые векторы за счёт второй компоненты лосса, а сами на каждой итерации выдают векторы, далёкие от текущих кодовых векторов, добавляется третье слагаемое. Оно отвечает за то, чтобы энкодер стремился выдавать векторы, близкие к кодовым векторам, а его значимость регулируется с помощью коэффициента .
Однако при обучении мы потеряли регуляризационное слагаемое , из-за чего распределение энкодера не было обязано приближать собой априорное распределение и осталось его узким подмножеством. Из-за этого с наибольшей вероятностью при семплировании из равномерного категориального распределения мы будем получать просто шумы вместо хороших картинок:
Чуть подробнее
При обучении обычного VAE мы минимизируем расстояние между априорным распределением и распределением, которое выдаёт энкодер, с помощью регуляризационного слагаемого .
Благодаря нему, например, двумерные латентные коды цифр MNIST приближённо распределяются по шарику — априорному нормальному распределению. А если каждой цифре выделить собственное латентное пространство (провести обуславливание на класс цифры), то априорное условное распределение для каждой цифры очень близко к нормальному.
А в случае VQ-VAE мы не можем заставить распределение, предсказываемое энкодером, быть равномерным категориальным, и получаем просто какое-то категориальное распределение с неизвестной параметризацией. Это напоминает ситуацию с обычным автоэнкодером: он тоже переводит входные картинки в латентное пространство, но семплировать из такого пространства мы не можем.
Чтобы исправить эту проблему, авторы предлагают с помощью дополнительной модели выучить априорное распределение тех латентных переменных, которые модель научилась генерировать в процессе обучения. Поскольку любое кодовое представление можно вытянуть в последовательность, а самих кодов — конечное наперёд заданное число, то эта задача близка к задаче обучения языковой модели.
Действительно, ведь там мы должны по последовательности предыдущих слов предложения предсказать следующее слово из доступного словаря, а в нашем случае — по входной последовательности дискретных латентных кодов предсказать следующий латентный код.
Для картинок авторы предложили моделировать априорное распределение латентных кодов с помощью PixelCNN. Детали архитектуры и обучения этой модели можно найти в оригинальной статье, здесь мы опишем только общую идею.
PixelCNN последовательно генерирует пиксели картинки, двигаясь из верхнего левого угла в правый нижний. Она проходит все ряды последовательно от верхнего до нижнего, а внутри каждого ряда движется слева направо:
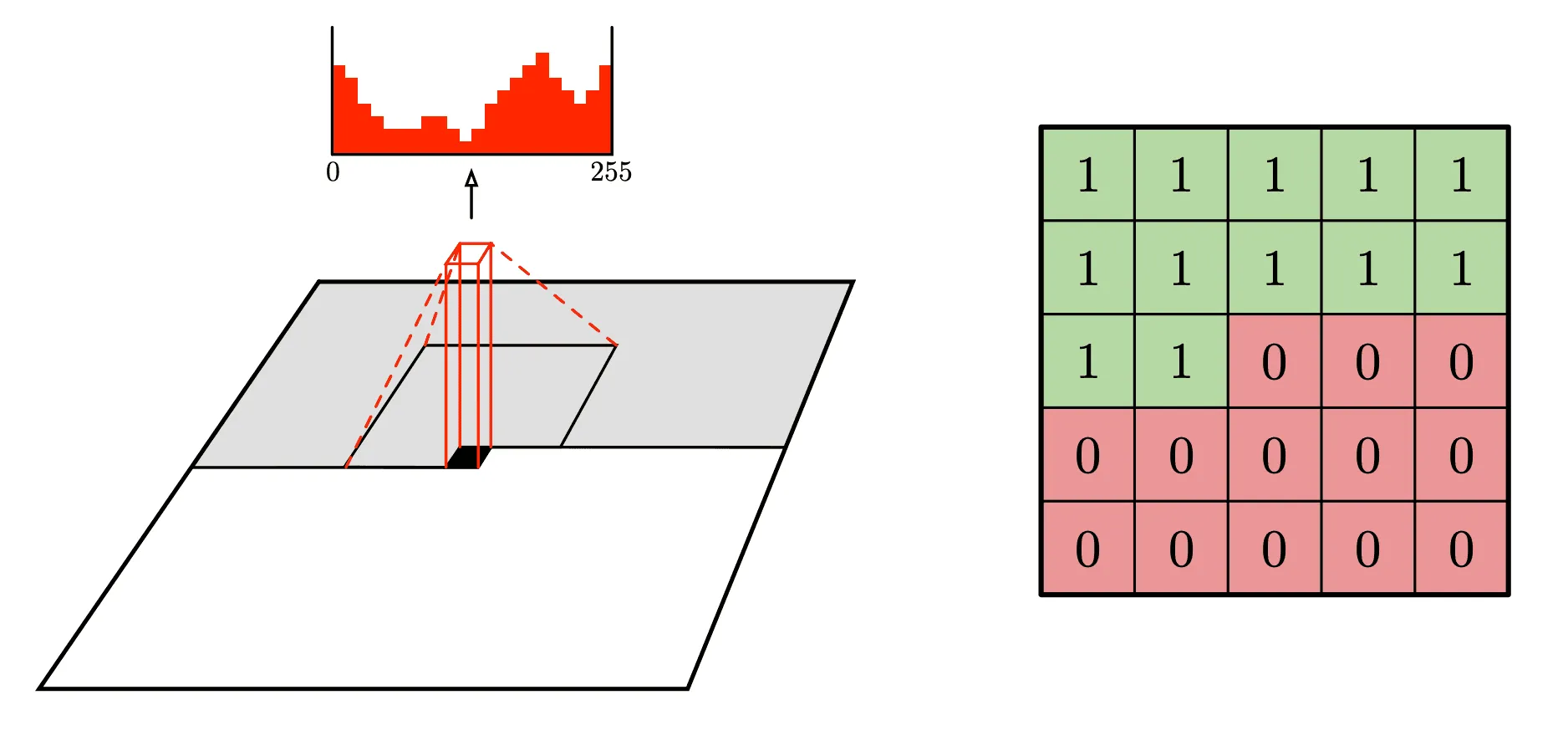
Для цветных картинок каналы (R, G, B) также моделируются последовательно: канал B при генерации зависит от R и G, а G — только от R. При предсказании значения каждого следующего пикселя модель использует значения уже сгенерированных соседей из некоторого окружающего квадрата. Чтобы модель не могла читать пиксели, идущие после текущего предсказываемого пикселя, используется специальная маска, пример которой изображён на правой части рисунка.
В случае VQ-VAE обучение PixelCNN происходит не на пикселях, а на латентных кодах. Семплирование из выученного априорного распределения выглядит гораздо лучше, чем попытки семплировать из равномерного:
Для аудио вместо PixelCNN авторами используется WaveNet. При обучении моделей априорных распределений есть возможность подавать метки классов, чтобы потом можно было семплировать из этих классов (принцип тот же, что и для CVAE).
Результаты реконструкции картинок из ImageNet с помощью VQ-VAE выглядят довольно неплохо (под реконструкцией понимается выход полной модели, состоящей из энкодера и декодера):
А так выглядят результаты семплирования из VQ-VAE с априорным распределением, выученным PixelCNN:
VQ-VAE-2
Модель VQ-VAE-2 — это расширение VQ-VAE. Она показывает значительный скачок по качеству генерируемых изображений:
Впечатляет то, что на картинке именно результат семплирования из выученного моделью распределения, а не результат реконструкции. Первое основное отличие модели VQ-VAE от VQ-VAE-2 — использование иерархических латентных переменных:
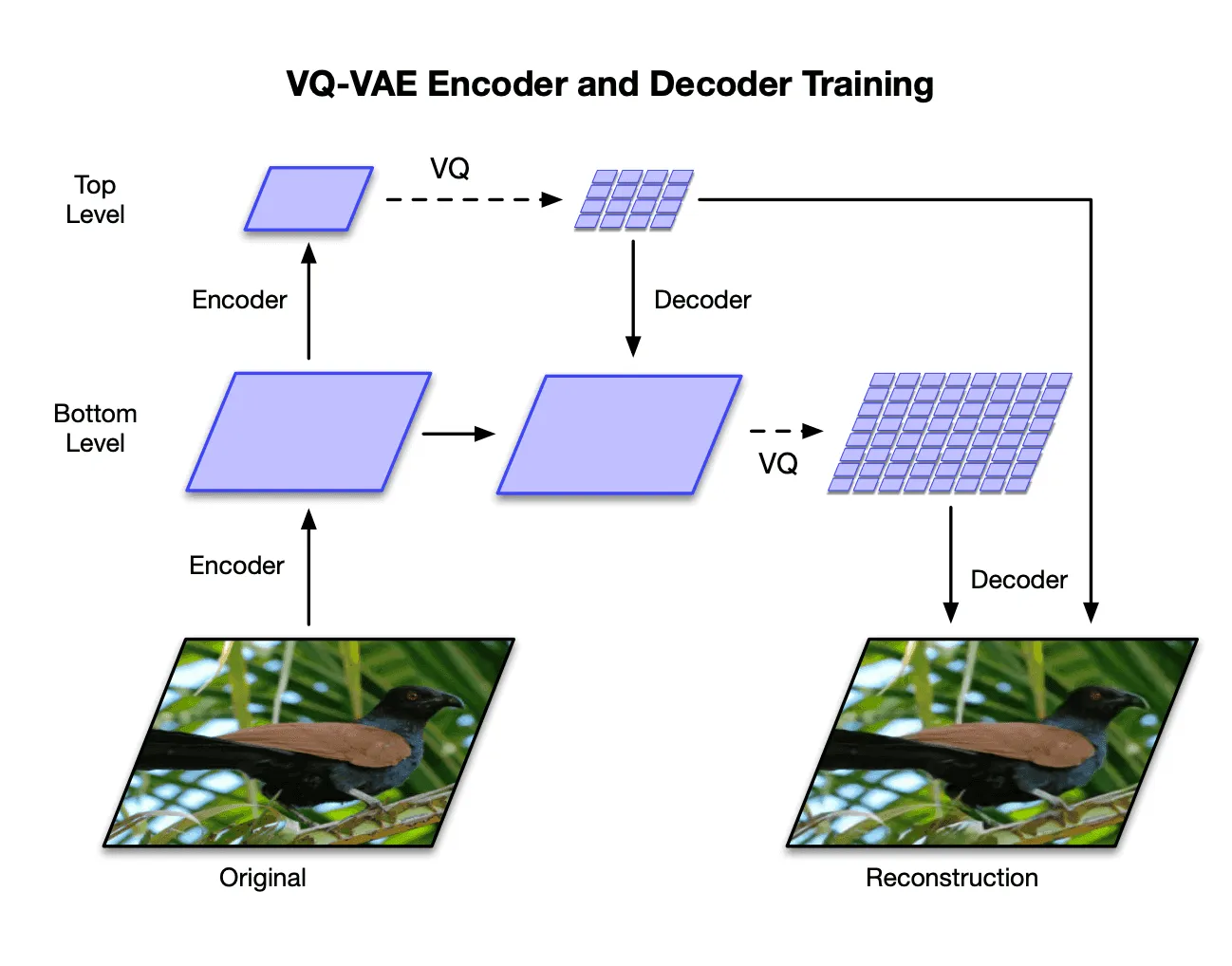
Прежде чем перейти к описанию архитектуры, хочется сделать небольшой дисклеймер: когда в тексте далее будет говориться «тензор размера », то будет иметься в виду, что тензор имеет шейп , где первая размерность соответствует батчам, а последняя — каналам.
На картинке показан пример двухуровневой архитектуры (хотя уровней может быть и больше). Каждому уровню соответствуют свои энкодер, декодер и набор кодовых векторов (общей размерности для всех уровней). Обозначим нижний и верхний энкодеры как и , а декодеры — как и .
- принимает на вход трёхканальную картинку размера пикселей, отображает её в тензор размера и передаёт на вход . выдаёт тензор размера , который затем отображается в тензор из кодовых векторов (квантизуется)
- передаётся на вход , затем выходы и конкатенируются и квантизуются в
- и конкатенируются и передаются на вход , который отображает их в исходную картинку
Для обучения модели используется почти такой же лосс, как для VQ-VAE. Для VQ-VAE он имел вид:
Для VQ-VAE-2 первое и третье слагаемые сохраняют свой вид, а второе слагаемое заменяется на обновление кодовых векторов с помощью экспоненциального скользящего среднего. Пусть — выход энкодера на шаге , выпрямленный в двумерный тензор, последняя размерность которого равна размерности кодовых векторов.
Пусть — множество из векторов, для которых на шаге ближайшим оказался кодовый вектор . Тогда обновление на шаге происходит по следующим формулам:
Здесь — некоторый вещественный параметр.
Так же, как и для VQ-VAE, априорное распределение для VQ-VAE-2 выучивается отдельно уже после обучения основной модели, но в случае VQ-VAE-2 оно имеет иерархическую структуру. На картинке изображён пример такого распределения для двухуровневой архитектуры:
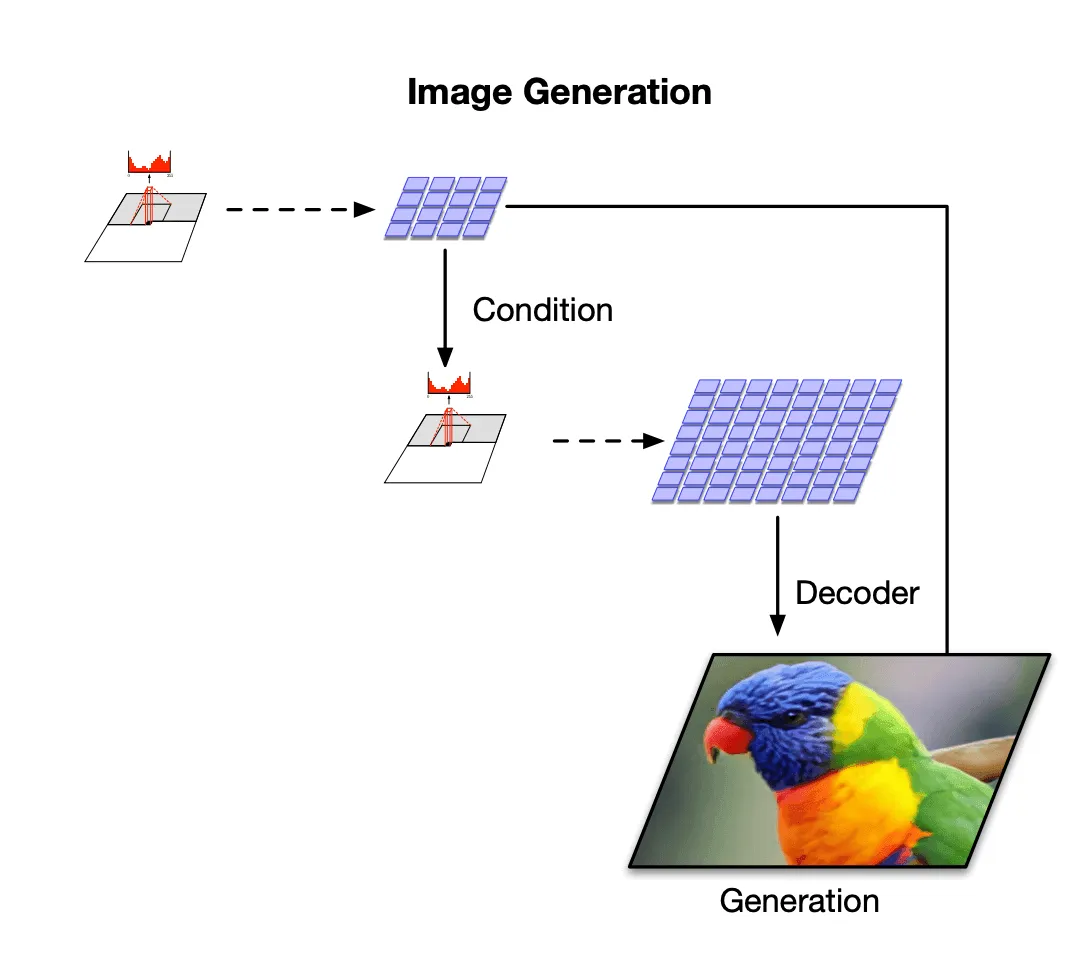
Для каждого уровня обучается отдельная модель PixelCNN: одна — на кодовых векторах первого уровня, вторая — на кодовых векторах первого и второго уровней. Обе модели также принимают на вход метку класса, изображение из которого нужно насемплировать.
Семплирование из финальной модели происходит так:
- семплируются векторы из верхнего распределения
- из нижнего распределения семплируются векторы при условии векторов
- декодер принимает на вход векторы и и выдаёт финальную картинку
Результаты семплирования из двухуровневой модели VQ-VAE-2, обученной на ImageNet:
А это — результаты семплирования из трёхуровневой модели VQ-VAE-2, обучавшейся на FFHQ:
DALL-E
Одна из недавних работ, связанных с VAE, — это DALL-E от OpenAI. Они обучили модель с 12 миллиардами параметров, генерирующую картинки по их текстовому описанию. Для обучения авторами был собран датасет, состоящий из 250 миллионов пар картинок и их описаний. Вот примеры работы этой модели:
В блог-посте OpenAI, посвящённом DALL-E, есть возможность самостоятельно составлять текстовые описания из некоторого ограниченного словаря и смотреть на результаты. Осторожно, это затягивает 😃
DALL-E идейно основывается на результатах VQ-VAE: сначала выучиваются кодовые векторы для картинок, а затем обучается Трансформер, моделирующий совместное априорное распределение текстов и кодовых векторов. Подробнее о трансформерах мы рассказывали в главе 6.3 этого хендбука.
В DALL-E задействована архитектура, основанная на декодер-части исходной архитектуры Трансформера, поэтому стоит также почитать про модель GPT-2, работающую аналогичным образом.
Обучение проходит в две стадии:
- Сначала обучается дискретизованный VAE (dVAE) c энкодером для сжатия RGB-картинок размера в тензор из кодовых векторов. Эта стадия обучения очень напоминает VQ-VAE, но вместо добавления в лосс дополнительных слагаемых для кодовых векторов авторы DALL-E используют релаксацию Гумбеля — трюк, позволяющий проводить честное дифференцирование по параметрам энкодера. Об обучении dVAE мы будем говорить подробнее далее.
- Затем обучается Трансформер (точнее, только декодер-часть исходной архитектуры Трансформера), задача которого — выучить совместное распределение картинок и их текстовых описаний. Он принимает на вход конкатенацию из эмбеддингов текстовых токенов и кодовых векторов картинок и учится для каждой входной последовательности предсказывать её продолжение. О некоторых деталях обучения Трансформера также будет рассказано далее.
Инференс обученной модели происходит так: эмбеддинги текстового описания картинки подаются на вход Трансформеру, и он авторегрессионно предсказывает кодовые векторы картинки, соответствующей этому описанию, а затем полученные кодовые векторы пропускаются через декодер dVAE.
dVAE
Обучение dVAE происходит путём максимизации ELBO для картинок и их дискретных латентных представлений :
где и — параметры энкодера и декодера дискретизованного VAE, a — равномерное категориальное распределение над кодовыми векторами. Здесь можно заметить дополнительный коэффициент , который в стандартном VAE всегда равен 1. Однако авторы DALL-E ввели дополнительный параметр , опираясь на результаты статьи о -VAE. Но, в отличие от исходной статьи, в их экспериментах значение постепенно понижается в ходе обучения.
Энкодер dVAE отображает картинки размера в тензор с шейпом , где — число кодовых векторов. То есть каждой из позиций энкодер сопоставляет категориальное распределение над кодовыми векторами, параметризованное выходными логитами.
Для получения тензора из кодовых векторов можно было бы сначала применить к распределениям на каждой из позиций, а затем сопоставить каждой позиции кодовый вектор, номеру которого соответствует максимальная вероятность (взять для этой позиции).
Однако операция не дифференцируема, и, к тому же, в концепции VAE на вход декодеру должен пойти семпл из распределения, предсказываемого энкодером, а взятие на каждой позиции не является семплированием из предсказанного распределения.
Поэтому нам потребуется применение некоторых трюков, которые позволят нам одновременно:
- аппроксимировать семплирование из
- сделать семплирование дифференцируемым
Gumbel-Max Trick и Gumbel-Softmax
Первый трюк известен в англоязычной литературе как Gumbel-Max Trick. Представим, что у нас есть логиты-выходы сетки , и мы хотим с их помощью получить семпл из категориального распределения, то есть стохастически предсказать класс. Для этого мы обычно применяем к логитам , чтобы получить вероятности :
а затем из получившегося категориального распределения семплируем класс. Оказывается, этим двум шагам будет эквивалентна следующая процедура:
- насемплировать числа из стандартного распределения Гумбеля,
- прибавить к каждому из логитов семпл ,
- выбрать класс , такой что .
О том, почему это действительно так, можно почитать здесь. Однако сам по себе Gumbel-Max Trick нам не поможет — ведь операция так и не стала дифференцируемой. Поэтому придётся использовать ещё один трюк, предложенный практически одновременно в двух статьях (первая и вторая) и названный Gumbel-Softmax в одной из них.
Чтобы описать этот трюк, отметим, что результат операции — это индекс некоторого класса . Такой индекс можно описать one-hot кодированием, то есть вектором длиной , в котором все элементы равны нулю, кроме -го, который равен единице.
Gumbel-Softmax состоит в том, чтобы вместо взятия на последнем этапе Gumbel-Max Trick делать следующее:
- вычислить , , — аппроксимацию one-hot при помощи с температурой
- сложить кодовые векторы с весами :
- выдать вектор в качестве латентного вектора для данной позиции
На самом деле авторы DALL-E не уточняли, как выходной вектор агрегируется из кодовых векторов и , но такой подход применён в реализации DALL-E на PyTorch.
При семплирование из распределения стремится к , и в процессе обучения dVAE авторы постепенно уменьшали значение . На следующей картинке слева — просто Gumbel-Max Trick, а справа — дифференцируемый вариант Gumbel-Max Trick:
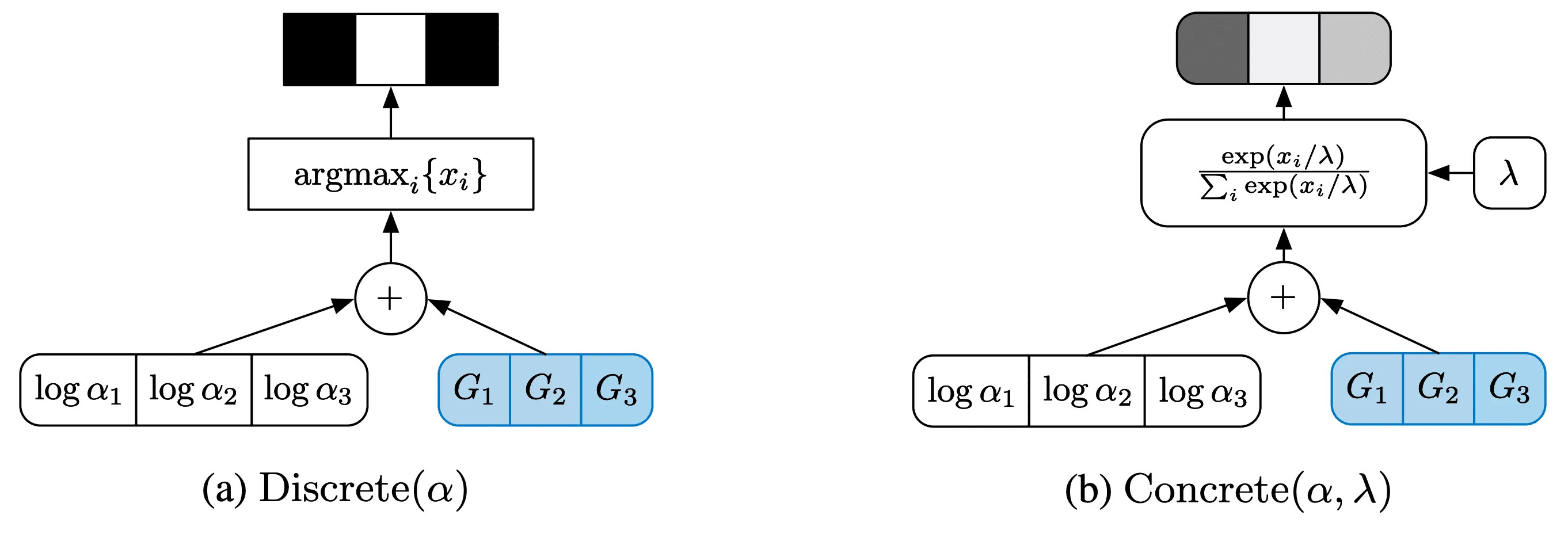
Таким образом, для обучения кодовых векторов для dVAE не требуется дополнительных слагаемых в лоссе относительно ELBO, а также копирования градиентов из декодера в энкодер (как было в VQ-VAE).
Кроме того, стоит отметить, что в данном случае не вырождается в константу, а действительно действует как регурялизатор, заставляя категориальное распределение, параметризованное логитами энкодера, быть ближе к равномерному распределению над кодовыми векторами.
Распределение Logit-Laplace
Ещё один трюк в обучении dVAE касается выходного распределения . Авторы DALL-E подметили проблему, возникающую при часто встречающемся выборе лапласовского и гауссовского распределений в качестве : оба они определены на всей вещественной прямой, в то время как пиксели принимают значения из ограниченного интервала. Таким образом, часть плотности при моделировании «теряется», оказываясь вне возможных границ значений пикселей.
Чтобы исправить эту проблему, авторы предлагают использовать распределение, которое они назвали “Logit-Laplace”. Его плотность определена на интервале и выражается следующей формулой:
Эта плотность соответствует случайной переменной, полученной применением сигмоиды к распределённой по Лапласу случайной переменной. Выражение для распределения Logit-Laplace можно получить по стандартной формуле для плотности случайной величины, полученной применением монотонной дифференцируемой функции к другой случайной величине (см. формулу, например, тут). Логарифм этой плотности подставляется в ELBO вместо .
Декодер на выходе выдаёт 6 тензоров: первые три соответствуют для RGB-каналов, оставшиеся три соответствуют , и эти 6 тензоров используются для подсчёта лосса. При подаче в энкодер значения картинок нормируются функцией :
Этим авторы добиваются того, чтобы декодер моделировал значения из , что позволяет нивелировать вычислительные проблемы, связанные с делением на в формуле плотности. Во время инференса реконструкция картинки вычисляется по формуле:
где — первые три тензора из выхода декодера. Выходы, соответствующие , при этом не используются.
Априорное распределение на текстах и картинках
На втором этапе авторы фиксируют параметры и и моделируют совместное распределение картинок и их текстовых описаний с помощью Sparse Transformer с 12 миллиардами параметров. На вход он получает конкатенацию из текстового описания картинки и её кодовых векторов. Картинка представляется 1024 кодовыми векторами, получаемыми из энкодера , причём при семплировании кодовых последовательностей используется обычный без добавления шума из распределения Гумбеля.
Текстовое описание токенизируется с помощью процедуры BPE (см. раздел про BPE здесь), и каждому токену ставится в соответствие представляющий его вектор из вещественных чисел (эмбеддинг). Для представления текста используется не более 256 токенов, а размер используемого словаря — 16 384 токена.
Задача Трансформера во время обучения — для каждого начального отрезка входной последовательности предсказать следующий за ним токен. Это может быть как текстовый токен, так и кодовый вектор картинки. Поскольку кодовые векторы картинок всегда идут за текстовыми токенами, при генерации кодовых векторов attention-механизм учитывает также и все предыдущие текстовые токены.
Кроме того, маска attention для кодовых векторов учитывает, что исходно они расположены не линейно друг за другом, а на прямоугольной сетке. В статье приводится несколько вариантов геометрических паттернов, которые использовались для attention-маски на кодовых векторах.
В качестве лосса используется взвешенная сумма кросс-энтропии для текстовых токенов и кросс-энтропии для кодовых векторов картинок c весами и соответственно (больший приоритет отдаётся генерации картнок, отсюда и больший вес для лосса).
Конечно, огромный Трансформер обучить крайне непросто, и очень существенная часть статьи посвящена трюкам, которые авторы применили для обучения такой большой модели.
Инференс
На этапе инференса в модель подаются токены текстового описания картинки, и на их основании модель авторегрессионно предсказывает кодовые векторы:
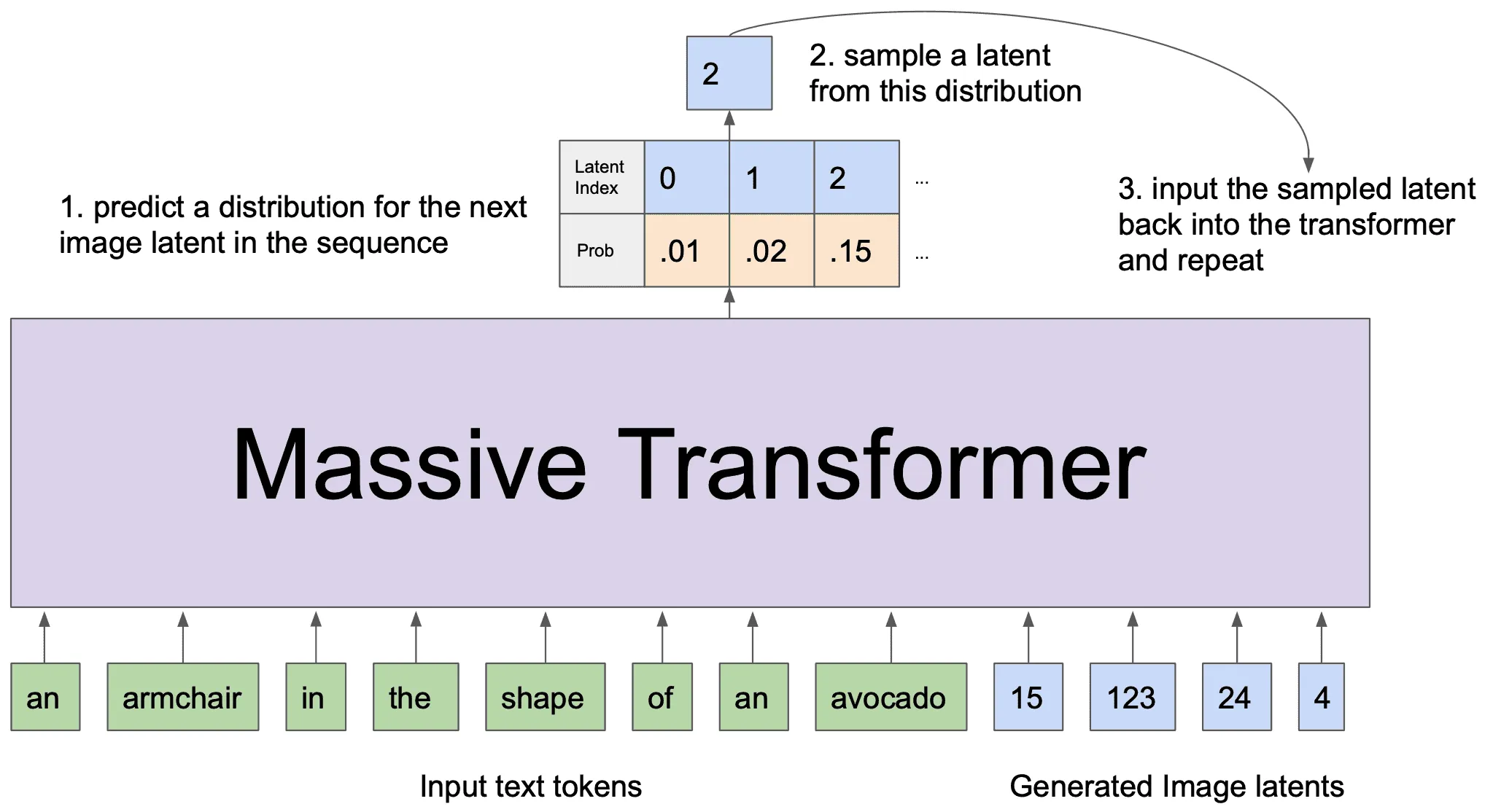
Кодовые векторы картинки подаются в декодер dVAE, который отображает их в финальную картинку:
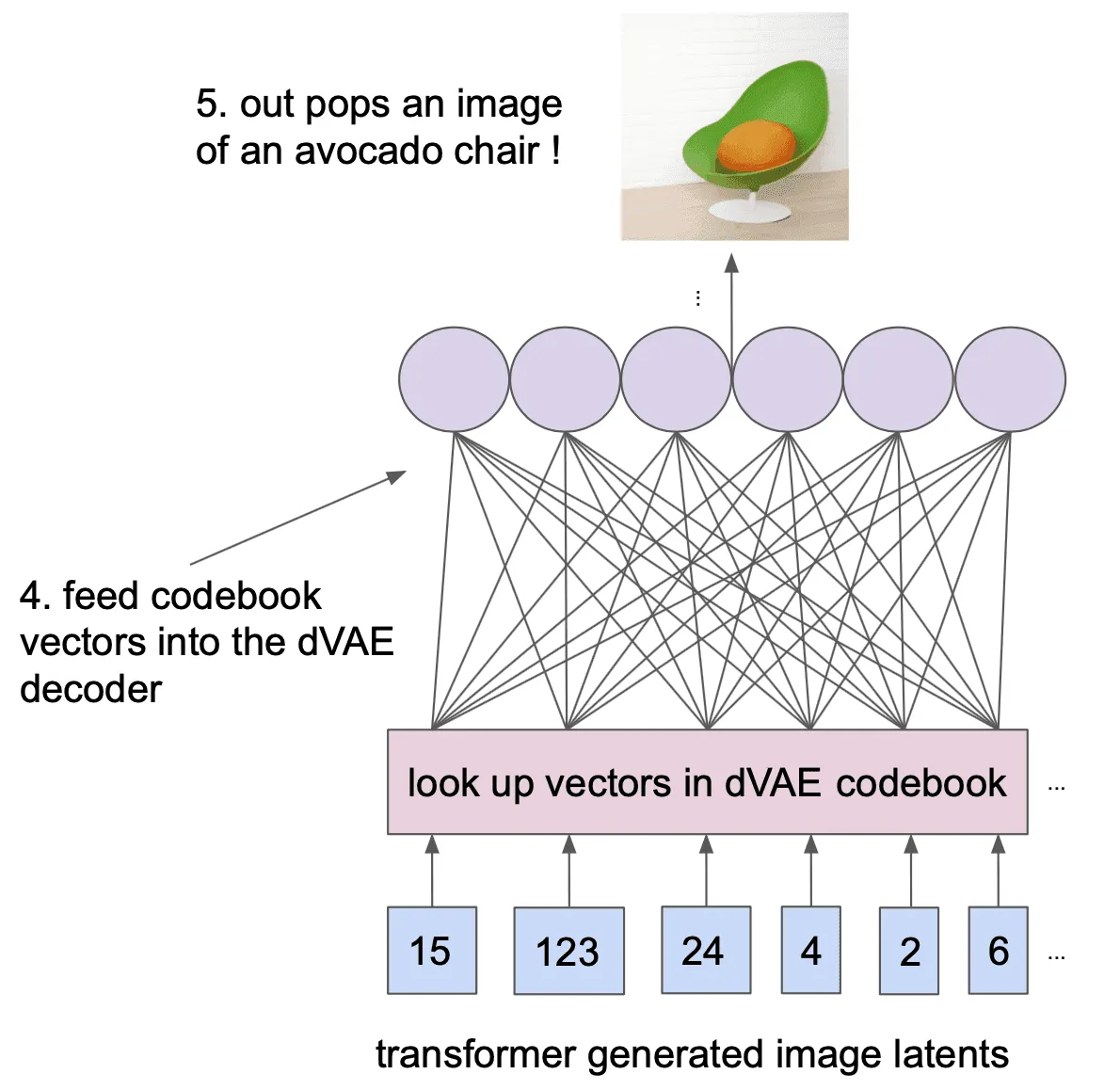
Для повышения качества предсказания авторы сначала генерируют 512 картинок для каждого текстового описания, а затем выбирают лучшую картинку из предсказанных. Разные наборы кодовых векторов для одного и того же текста можно получить, например, случайно выбирая на каждом шаге генерации какой-то кодовый вектор согласно предсказанному Трансформером распределению. Ранжирование полученных 512 картинок осуществляется с помощью CLIP — большой нейросети, обучавшейся в режиме без учителя на большом количестве данных моделировать совместное распределение картинок и текстов.
Заключение
Итак, в этом параграфе мы поговорили о том, как устроен VAE в классическом смысле, — с непрерывным распределением латентных переменных, а также поговорили о работах, основанных на идеях использования дискретных распределений для VAE.
Конечно, различные модификации VAE не исчерпываются только лишь отказом от непрерывных латентных переменных в пользу дискретных. Есть множество других возможных направлений для улучшения модели: использование иерархических латентных распределений (которые мы, кстати, видели в контексте VQ-VAE-2), использование функций потерь, отличающихся от ELBO, выбор различных форм латентных пространств, применение adversarial-обучения и многое другое.
Хороший список различных статей, посвящённых модификациям VAE, можно найти здесь. Из недавних работ, связанных с применением иерархических распределений, интересной кажется NVAE — семплы из модели выглядят весьма впечатляюще. Про неё есть хороший видеообзор от Yannic Kilcher.
На этом мы завершаем рассказ о VAE. Будем надеяться, что он дал вам общее представление и об исходных идеях, из которых выросла модель VAE, и о наиболее интересных последних результатах, связанных с ней.
А в следующем параграфе мы поговорим о генеративно-состязательных сетях.