Нейронные сети обучаются с помощью тех или иных модификаций градиентного спуска, а чтобы применять его, нужно уметь эффективно вычислять градиенты функции потерь по всем обучающим параметрам. Казалось бы, для какого-нибудь запутанного вычислительного графа это может быть очень сложной задачей, но на помощь спешит метод обратного распространения ошибки.
Метод обратного распространения ошибки (backward propagation)
Открытие метода обратного распространения ошибки стало одним из наиболее значимых событий в области искусственного интеллекта. В актуальном виде он был предложен в 1986 году Дэвидом Э. Румельхартом, Джеффри Э. Хинтоном и Рональдом Дж. Вильямсом, а также независимо и одновременно красноярскими математиками С. И. Барцевым и В. А. Охониным.
С тех пор для нахождения градиентов параметров нейронной сети используется метод вычисления производной сложной функции, и оценка градиентов параметров сети стала хоть и сложной инженерной задачей, но уже не искусством. Несмотря на простоту используемого математического аппарата, появление этого метода привело к значительному скачку в развитии искусственных нейронных сетей.
Суть метода можно записать одной формулой, тривиально следующей из формулы производной сложной функции: если , то . Уже сейчас мы видим, что градиенты можно вычислять последовательно, в ходе одного обратного прохода, начиная с и умножая каждый раз на частные производные предыдущего слоя.
Backward propagation в одномерном случае
В одномерном случае всё выглядит особенно просто. Пусть — переменная, по которой мы хотим продифференцировать , причём сложная функция имеет вид
где все скалярные. Тогда
Суть этой формулы такова. Если мы уже совершили прямой проход (forward propagation), значит мы уже знаем
Поэтому мы можем действовать следующим образом:
-
берём производную в точке ;
-
умножаем на производную в точке ;
-
и так далее, пока не дойдём до производной в точке .
Проиллюстрируем это на картинке, расписав по шагам дифференцирование по весам функции потерь логистической регрессии на одном объекте (то есть для батча размера 1):
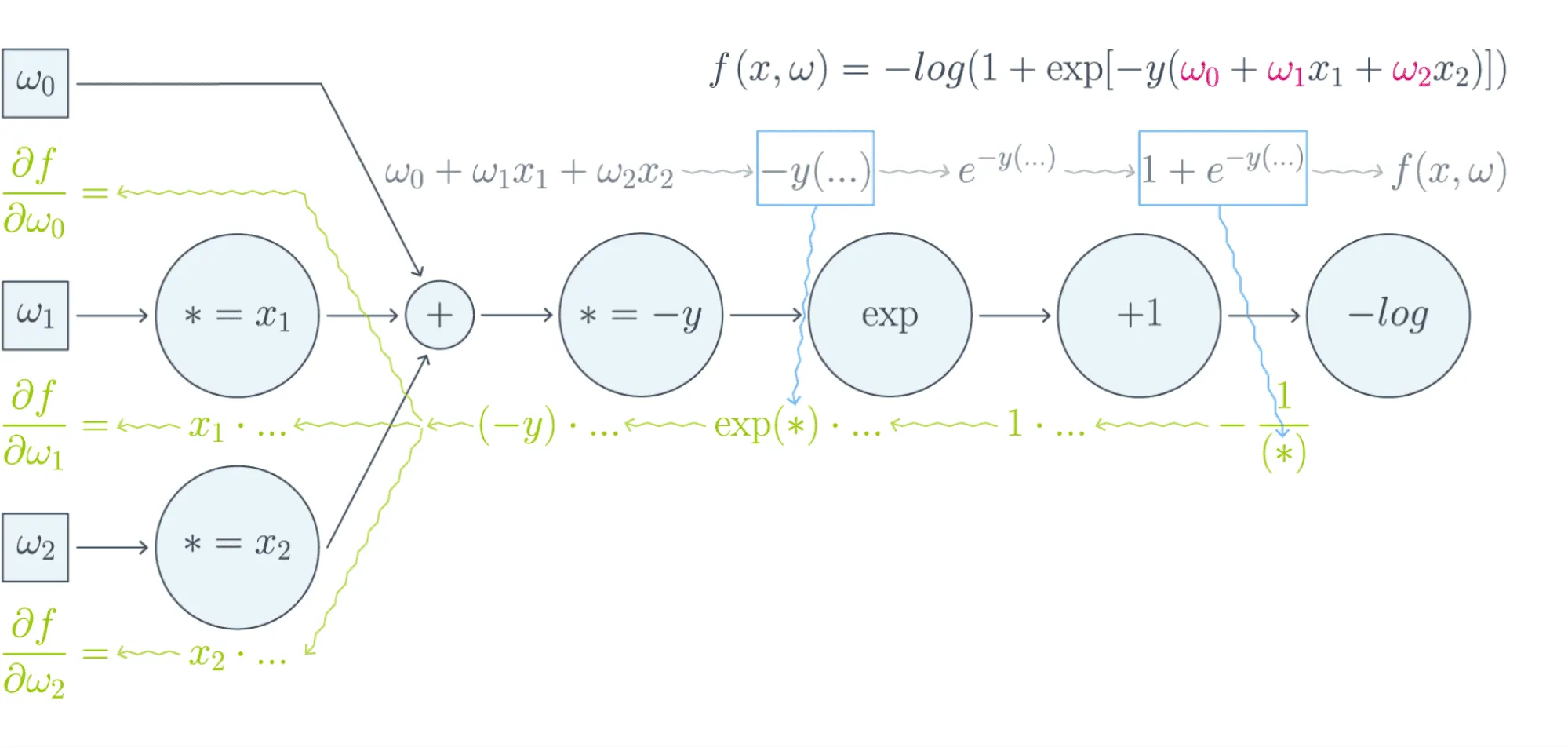
Собирая все множители вместе, получаем:
Таким образом, сперва совершается forward propagation для вычисления всех промежуточных значений (да, все промежуточные представления нужно будет хранить в памяти), а потом запускается backward propagation, на котором в один проход вычисляются все градиенты.
Почему же нельзя просто пойти и начать везде вычислять производные?
В параграфе, посвящённом матричным дифференцированиям, мы поднимаем вопрос о том, что вычислять частные производные по отдельности — это зло, лучше пользоваться матричными вычислениями. Но есть и ещё одна причина: даже и с матричной производной в принципе не всегда хочется иметь дело.
Рассмотрим простой пример. Допустим, что и — два последовательных промежуточных представления и , связанных функцией . Предположим, что мы как-то посчитали производную функции потерь , тогда
И мы видим, что, хотя оба градиента и — это просто матрицы, в ходе вычислений возникает «четырёхмерный кубик» . Его болезненно даже хранить: уж больно много памяти он требует —м по сравнению с безобидными , требуемыми для хранения градиентов.
Поэтому хочется промежуточные производные рассматривать не как вычисляемые объекты , а как преобразования, которые превращают в .
Целью следующих параграфов будет именно это: понять, как преобразуется градиент в ходе error backward propagation при переходе через тот или иной слой.
Вы спросите себя: надо ли мне сейчас пойти и прочитать параграф учебника про матричное дифференцирование?
Короткий ответ: Зависит от ваших знаний.
Длинный ответ: Найдите производную функции по вектору :
А как всё поменяется, если тоже зависит от ? Чему равен градиент функции, если является скаляром?
Если вы готовы прямо сейчас взять ручку и бумагу и посчитать всё, то вам, вероятно, не надо читать про матричные дифференцирования. Но мы советуем всё-таки заглянуть в этот параграф, если обозначения, которые мы будем дальше использовать, покажутся вам непонятными: единой нотации для матричных дифференцирований человечество пока, увы, не изобрело, и переводить с одной на другую не всегда легко.
А мы же сразу перейдём к интересующей нас вещи: к вычислению градиентов сложных функций.
Градиент сложной функции
Напомним, что формула производной сложной функции выглядит следующим образом:
Теперь разберёмся с градиентами. Пусть – скалярная функция. Тогда
С другой стороны,
То есть — применение сопряжённого к линейного отображения к вектору .
Эта формула — сердце механизма обратного распространения ошибки. Она говорит следующее: если мы каким-то образом получили градиент функции потерь по переменным из некоторого промежуточного представления нейронной сети и при этом знаем, как преобразуется градиент при проходе через слой между и (то есть как выглядит сопряжённое к дифференциалу слоя между ними отображение), то мы сразу же находим градиент и по переменным из :
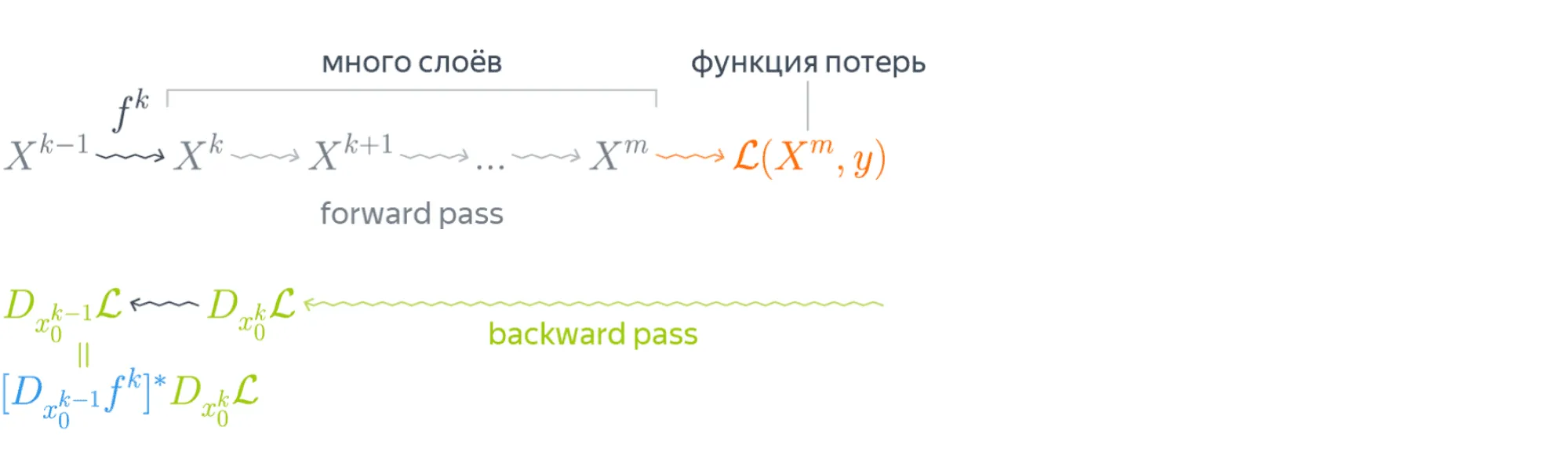
Таким образом слой за слоем мы посчитаем градиенты по всем вплоть до самых первых слоёв.
Далее мы разберёмся, как именно преобразуются градиенты при переходе через некоторые распространённые слои.
Градиенты для типичных слоёв
Рассмотрим несколько важных примеров.
Пример №1
, где — вектор, а – поэлементное применение :
Тогда, как мы знаем,
Следовательно,
где означает поэлементное перемножение. Окончательно получаем
Отметим, что если и — это просто векторы, то мы могли бы вычислять всё и по формуле .
В этом случае матрица была бы диагональной (так как зависит только от : ведь берётся поэлементно), и матричное умножение приводило бы к тому же результату. Однако если и — матрицы, то представлялась бы уже «четырёхмерным кубиком», и работать с ним было бы ужасно неудобно.
Пример №2
, где и — матрицы. Как мы знаем,
Тогда
Здесь через мы обозначили отображение , а в предпоследнем переходе использовалось следующее свойство следа:
где — произвольные матрицы подходящих размеров (то есть допускающие перемножение в обоих приведённых порядках). Следовательно, получаем
Пример №3
, где и — матрицы. Для приращения имеем
Тогда
Здесь через обозначено отображение . Значит,
Пример №4
, где — матрица , а — функция, которая вычисляется построчно, причём для каждой строки :
В этом примере нам будет удобно воспользоваться формализмом с частными производными. Сначала вычислим для одной строки , где через мы для краткости обозначим . Нетрудно проверить, что
Так как softmax вычисляется независимо от каждой строчки, то
где через мы обозначили для краткости .
Теперь пусть (пришедший со следующего слоя, уже известный градиент). Тогда
Так как при , мы можем убрать суммирование по :
Таким образом, если мы хотим продифференцировать в какой‑то конкретной точке , то, смешивая математические обозначения с нотацией Python, мы можем записать:
Backward propagation в общем виде
Подытожим предыдущее обсуждение, описав алгоритм error backward propagation (алгоритм обратного распространения ошибки). Допустим, у нас есть текущие значения весов и мы хотим совершить шаг SGD по мини-батчу . Мы должны сделать следующее:
- Совершить forward propagation, вычислив и запомнив все промежуточные представления .
- Вычислить все градиенты с помощью backward propagation.
- С помощью полученных градиентов совершить шаг SGD.
Проиллюстрируем алгоритм на примере двухслойной нейронной сети со скалярным output. Для простоты опустим свободные члены в линейных слоях.
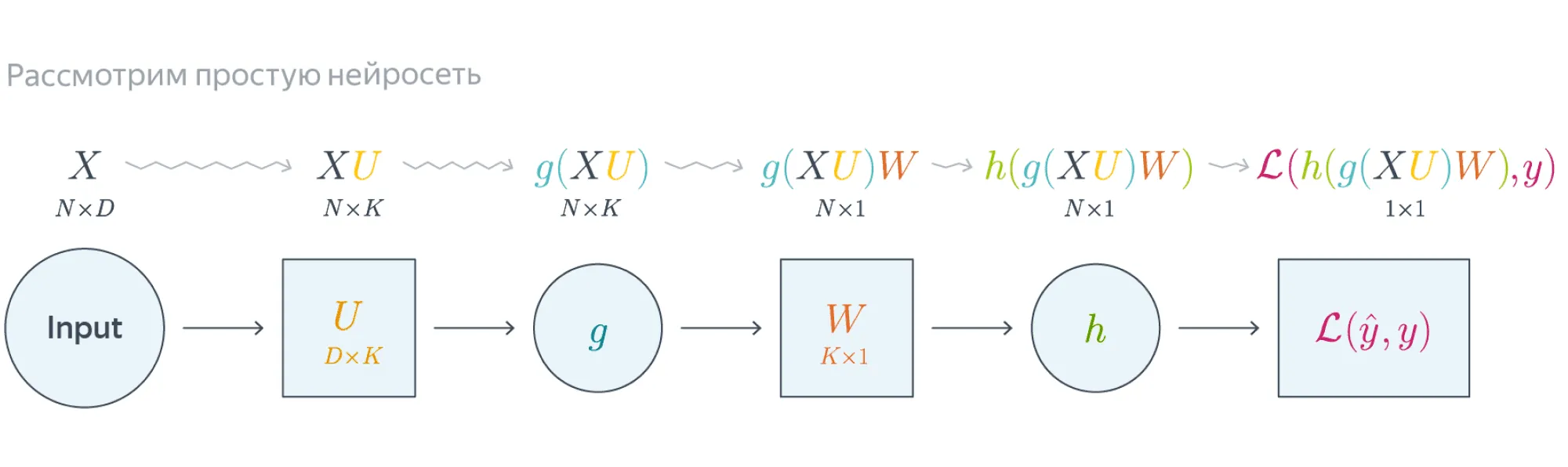
Обучаемые параметры – матрицы и . Как найти градиенты по ним в точке ?
Итого матрица , как и .
Итого , как и
Схематически это можно представить следующим образом:
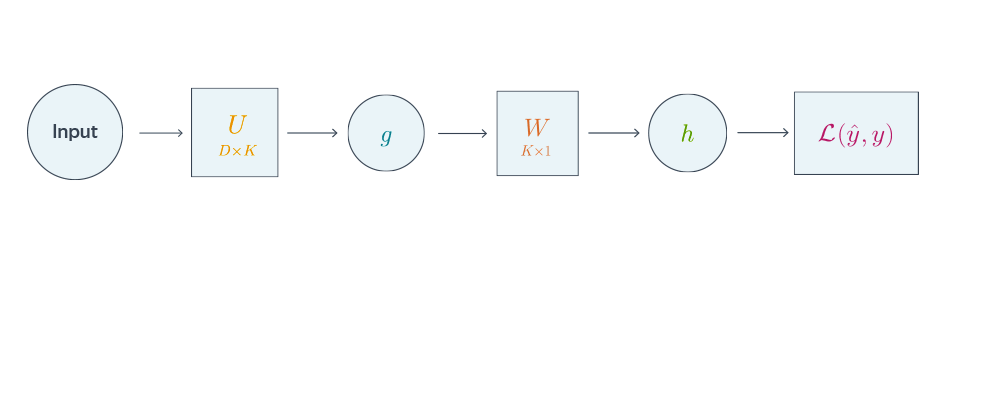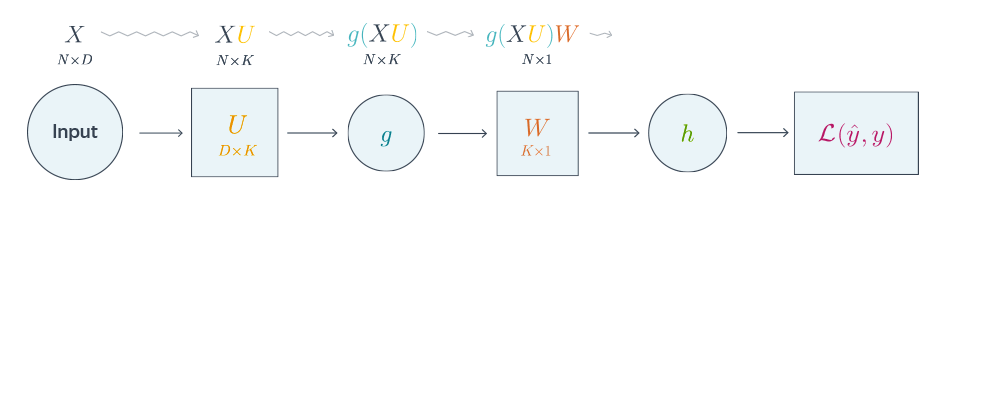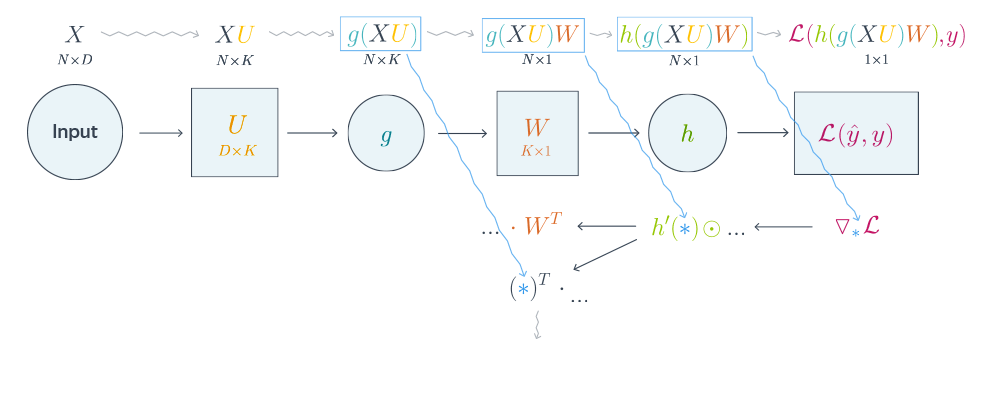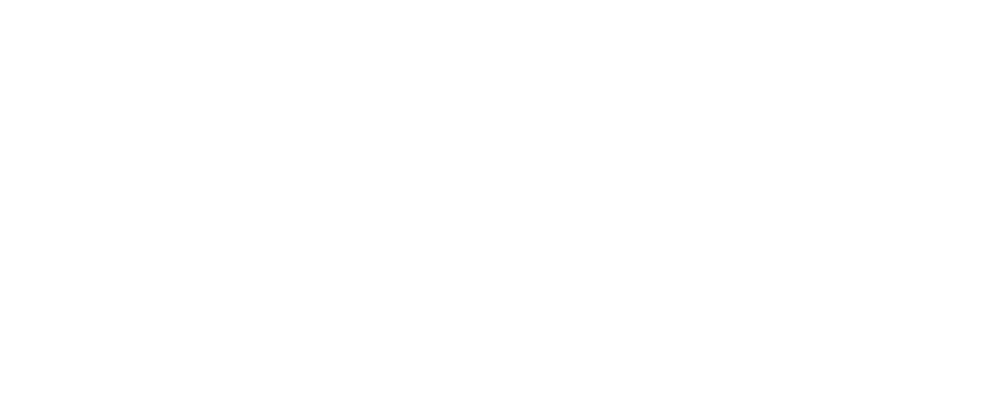
Backward propagation для двухслойной нейронной сети
Если вы не уследили за вычислениями в предыдущем примере, давайте более подробно разберём его чуть более конкретную версию (для )
Рассмотрим двуслойную нейронную сеть для классификации. Мы уже встречали её ранее при рассмотрении линейно неразделимой выборки. Предсказания получаются следующим образом:
Пусть и — текущее приближение матриц весов. Мы хотим совершить шаг по градиенту функции потерь, и для этого мы должны вычислить её градиенты по и в точке .
Прежде всего мы совершаем forward propagation, в ходе которого мы должны запомнить все промежуточные представления: , , , . Они понадобятся нам дальше.
Для полученных предсказаний вычисляется значение функции потерь:
Дальше мы шаг за шагом будем находить производные по переменным из всё более глубоких слоёв.
-
Градиент по предсказаниям имеет вид
где, напомним, (обратите внимание на то, что и тут именно те, из которых мы делаем градиентный шаг).
-
Следующий слой — поэлементное взятие . Как мы помним, при переходе через него градиент поэлементно умножается на производную , в которую подставлено предыдущее промежуточное представление:
Аналогичным образом
-
Следующий слой — снова взятие .
-
Наконец, последний слой — это умножение на . Тут мы дифференцируем только по :
Итоговые формулы для градиентов получились страшноватыми, но они были получены друг из друга итеративно с помощью очень простых операций: матричного и поэлементного умножения, в которые порой подставлялись значения заранее вычисленных промежуточных представлений.
Автоматизация и autograd
Итак, чтобы нейросеть обучалась, достаточно для любого слоя с параметрами уметь:
- превращать в (градиент по выходу в градиент по входу);
- считать градиент по его параметрам .
При этом слою совершенно не надо знать, что происходит вокруг. То есть слой действительно может быть запрограммирован как отдельная сущность, умеющая внутри себя делать forward propagation и backward propagation, после чего слои механически, как кубики в конструкторе, собираются в большую сеть, которая сможет работать как одно целое.
Более того, во многих случаях авторы библиотек для глубинного обучения уже о вас позаботились и создали средства для автоматического дифференцирования выражений (autograd). Поэтому, программируя нейросеть, вы почти всегда можете думать только о forward-проходе, прямом преобразовании данных, предоставив библиотеке дифференцировать всё самостоятельно.
Это делает код нейросетей весьма понятным и выразительным (да, в реальности он тоже бывает большим и страшным, но сравните на досуге код какой-нибудь разухабистой нейросети и код градиентного бустинга на решающих деревьях и почувствуйте разницу).
Но это лишь начало
Метод обратного распространения ошибки позволяет удобно посчитать градиенты, но дальше с ними что-то надо делать, и старый добрый SGD едва ли справится с обучением современной сетки. Так что же делать? О некоторых приёмах мы расскажем в следующем параграфе.




