Классификационные модели, которые мы рассматривали в предыдущих параграфах, нацелены непосредственно на оценку . Такие модели называются дискриминативными.
К ним относится, например, логистическая регрессия: она предлагает оценку . В процессе обучения дискриминативные модели подбирают разделяющую поверхность (гиперплоскость в случае логистической регрессии). Новые объекты дискриминативная модель классифицирует в зависимости от того, по какую сторону от разделяющей поверхности они лежат.
Например, обучившись на изображениях домашних кошек (y=0) и рысей (y=1), дискриминативная модель будет определять, новое изображение больше похоже на кошку или на рысь. При этом, если на вход такой модели дать изображение собаки (объект класса, которого не было в обучении, выброс), дискриминативная модель заведомо не сможет обнаружить, что это и не кошка, и не рысь, и отнесёт такой объект к одному из «знакомых» ей классов.
В этом параграфе мы поговорим о другой группе моделей, которые нацелены на оценку . Такая модель описала бы, как обычно выглядят кошки, как они могут выглядеть, а каких кошек точно не бывает. Так же она описала бы и рысей. Она также определила бы по обучающим данным, насколько изображения кошек встречаются чаще, чем изображения рысей, т.е. оценила бы .
Генеративный и дискриминативный подходы к обучению
Если модель позволила точно оценить распределение , с её помощью можно генерировать объекты из этого условного распределения, в нашем примере — изображения кошек и рысей соответственно.
А вместе распределение дало бы нам возможность генерировать изображения и кошек, и рысей, причём именно в той пропорции, в которой они встречаются в реальном мире. Поэтому модели, оценивающие , называют генеративными. Ещё одно достоинство генеративных моделей — их способность находить выбросы в данных: объект можно считать выбросом, если мало для каждого класса .
Заметим, что находить выбросы с помощью генеративной модели можно и когда класс всего один — то есть никакие метки классов не доступны. Такая задача называется одноклассовой классификацией. Например, если у нас есть не размеченный датасет с аудиозаписями речи людей, то, обучив на нём генеративную модель, оценивающую в данном случае , мы сможем для нового аудио определить, похоже ли оно на аудиозапись человеческой речи (значение велико), или это что-то другое: синтезированная речь, посторонний шум и т.п. (значение мало).
Если мы знаем, что «выбросы», с которыми модели предстоит сталкиваться, — это, как правило, синтезированная речь, то, мы можем дополнить датасет вторым классом, состоящим из синтезированной речи, и смоделировать также распределение этого класса. Это позволит существенно увеличить качество детектирования таких выбросов.
Чтобы использовать генеративную модель для классификации, необходимо выразить через и . Сделать это позволяет формула Байеса:
Классификация в генеративных моделях осуществляется с помощью байесовского классификатора:
Оценить , как правило, несложно. Для этого используют частотные оценки, полученные в обучающей выборке:
Отметим ещё раз, что использование генеративного подхода позволяет внедрять в модель априорные знания о . Это не очень впечатляет, когда речь идёт о бинарной классификации, но всё меняется, если рассмотреть задачу ASR (автоматического распознавания речи), в которой по записи голоса восстанавливается произносимый текст.
Таргетами здесь могут быть любые предложения или даже более развёрнутые тексты. При этом размеченных данных (запись, текст) обычно намного меньше, чем доступных текстов, и обученная на большом чисто текстовом корпусе языковая модель, которая будет оценивать вероятность того или иного предложения, может стать большим подспорьем, позволив из нескольких фонетически корректных наборов слов выбрать тот, который в большей степени похож на настоящее предложение.
Но как смоделировать распределение ? Пространство всех возможных функций распределения бесконечномерно, из-за чего оценить произвольное распределение с помощью конечной выборки невозможно. Поэтому перед оценкой на это распределение накладывают дополнительные ограничения. Некоторые простые примеры таких ограничений мы рассмотрим в следующих разделах.
Gaussian discriminant analysis
Модель гауссовского (или квадратичного) дискриминантного анализа (GDA) строится в предположении, что распределение объектов каждого класса подчиняется многомерному нормальному закону со средним и ковариационной матрицей :
Тогда функция правдоподобия
достигает максимума при
И , представленной выше см. выражение .
Рассмотрим, как выглядит разделяющая поверхность в модели GDA. На поверхности, разделяющей классы и выполняется
Поскольку левая часть уравнения (2) квадратична по , разделяющая поверхность между двумя классами будет представлять из себя гиперповерхность порядка 2. Пример разделяющей поверхности многоклассовой модели GDA приведён на рис.

Плотность классов и разделяющая поверхность в многоклассовой модели LDA см. рисунок.

Linear Discriminant Analysis
В выражении (2) член второго порядка зануляется при . Таким образом, если дополнительно предположить, что все классы имеют общую ковариационную матрицу , разделяющая поверхность между любыми двумя классами будет линейной (см. рисунок). Поэтому такая модель называется линейным дискриминантным анализом (LDA).
На этапе обучения единственное отличие модели LDA от GDA состоит в оценке ковариационной матрицы:
Заметим, что в модели GDA для каждого класса требовалось оценить порядка параметров. Это может привести к переобучению в случае, если размерность пространства признаков велика, а некоторые классы представлены в обучающей выборке малым количеством объектов. В LDA для каждого класса требуется оценить лишь порядка параметров (значение и элементы вектора ), и ещё общих для всех классов параметров (элементы матрицы ).
Таким образом, основное преимущество модели LDA перед GDA — её меньшая склонность к переобучению, недостаток — линейная разделяющая поверхность.
Метод наивного байеса
Предположим, что признаки объектов каждого класса — независимые случайные величины:
В таком случае говорят, что величины условно независимы относительно . Тогда справедливо
То есть для того, чтобы оценить плотность многомерного распределения достаточно оценить плотности одномерных распределений , см. рисунок.
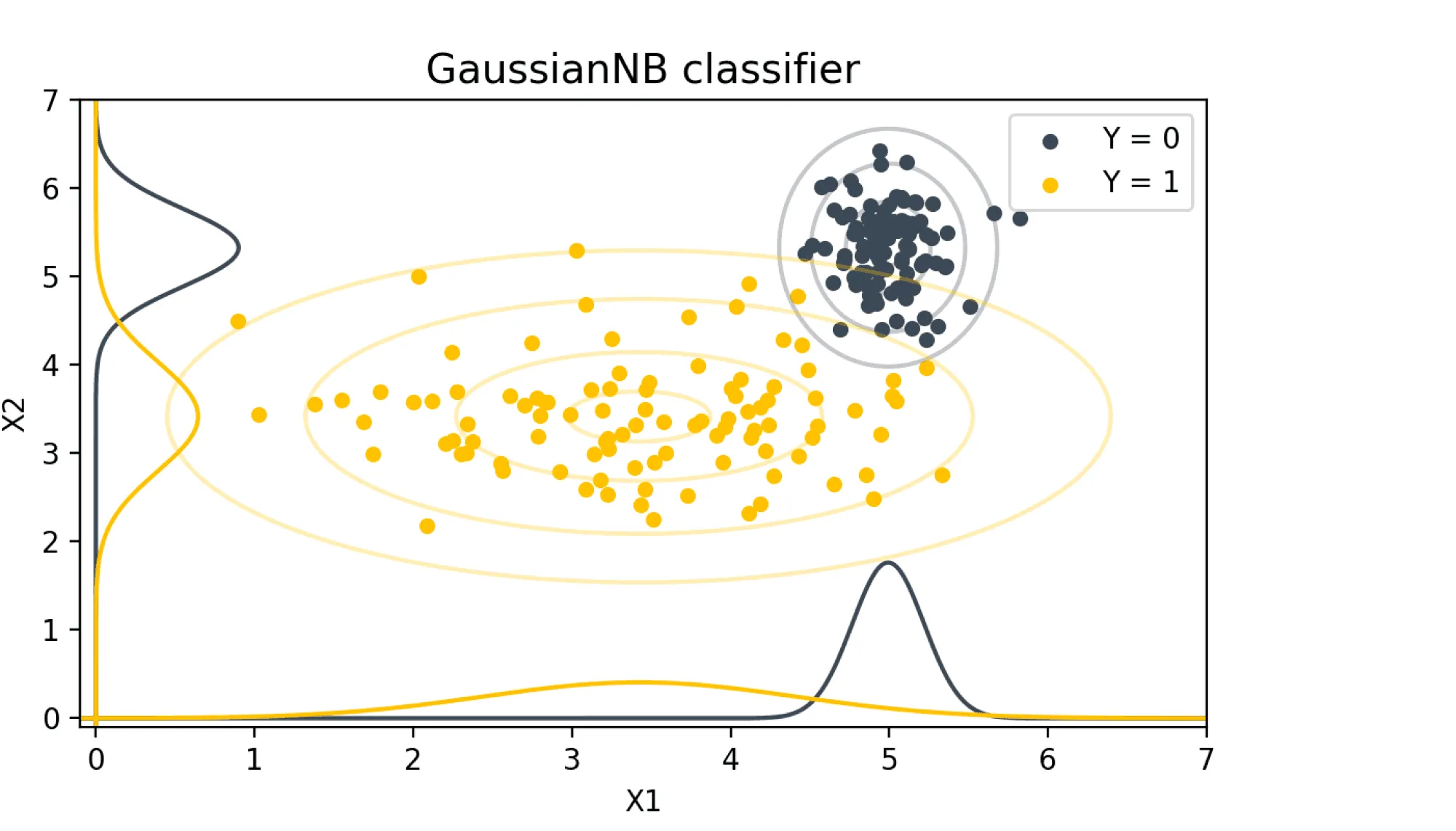
На рисунке приведён пример условно независимых относительно случайных величин . Для оценки плотности двумерных распределений объектов классов достаточно оценить плотности маргинальных распределений, изображённые графиками вдоль осей.
Рассмотрим пример. Пусть решается задача классификации отзывов об интернет-магазине на 2 категории: — отрицательный отзыв, клиент остался не доволен, и — положительный отзыв. Пусть признак равен 1, если слово присутствует в отзыве, и 0 иначе. Тогда условие выражения означает, что, в частности, наличие или отсутствие слова «дозвониться» в отрицательном отзыве не влияет на вероятность наличия в этом отзыве слова «телефон».
На практике в процессе feature engineering почти всегда создаётся много похожих признаков, и условно независимые признаки можно встретить очень редко. Поэтому генеративную модель, построенную в предположении условия выражения , называют наивным байесовским классификатором (Naive Bayes classifier, NB).
Обучение модели NB заключается в оценке распределений и . Для можно использовать частотную оценку выражения . — одномерное распределение. Рассмотрим несколько способов оценки одномерного распределения.
Оценка одномерного распределения
Пусть мы хотим оценить одномерное распределение .
Если распределение дискретное, требуется оценить его функцию массы, то есть вероятность того, что величина примет значение . Метод максимума правдоподобия приводит к частотной оценке:
Где — размер выборки, по которой оценивается распределение (количество объектов класса в случае оценки плотности класса ).
При этом может оказаться, что некоторое значение ни разу не встречается в обучающей выборке. Например, в случае классификации отзывов методом Наивного Байеса, слово «амбивалентно» не встретилось ни в одном положительном отзыве, но встретилось в отрицательных. Тогда использование оценки выражения приведёт к тому, что все отзывы с этим словом будут определяться NB как отрицательные с вероятностью 1. Чтобы избежать принятия таких радикальных решений при недостатке статистики, используют сглаживание Лапласа:
где — количество различных значений, принимаемых случайной величиной , — гиперпараметр.
Для оценки плотности абсолютно непрерывного распределения в точке можно разделить количество объектов обучающей выборки в окрестности точки на размер этой окрестности:
Обычно объекты, лежащие дальше от точки , учитывают с меньшим весом. Таким образом, оценка плотности приобретает вид
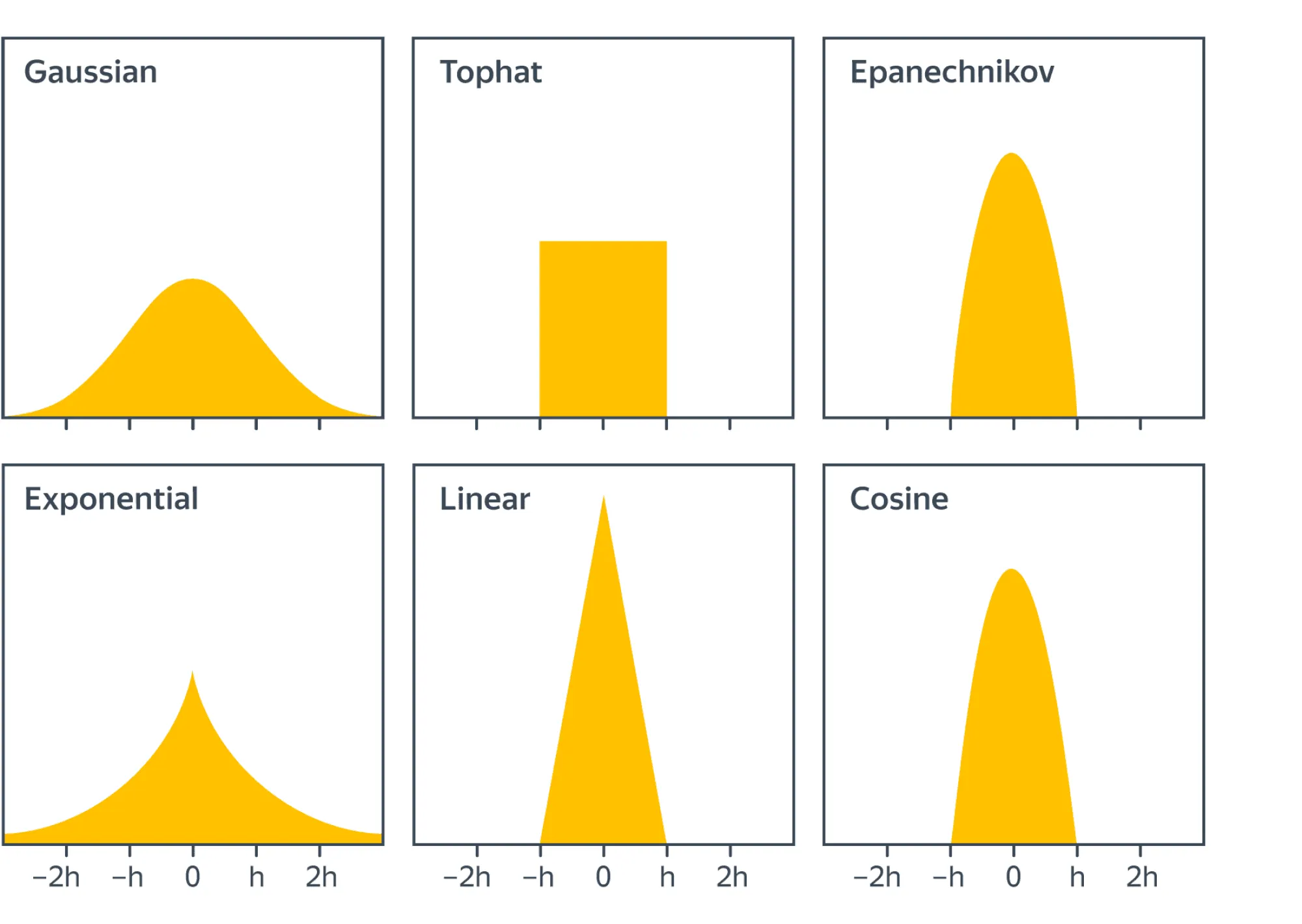
где функция , называемая ядром, обычно имеет носитель (см. рисунок ниже). Такой способ оценки плотности называют непараметрическим.
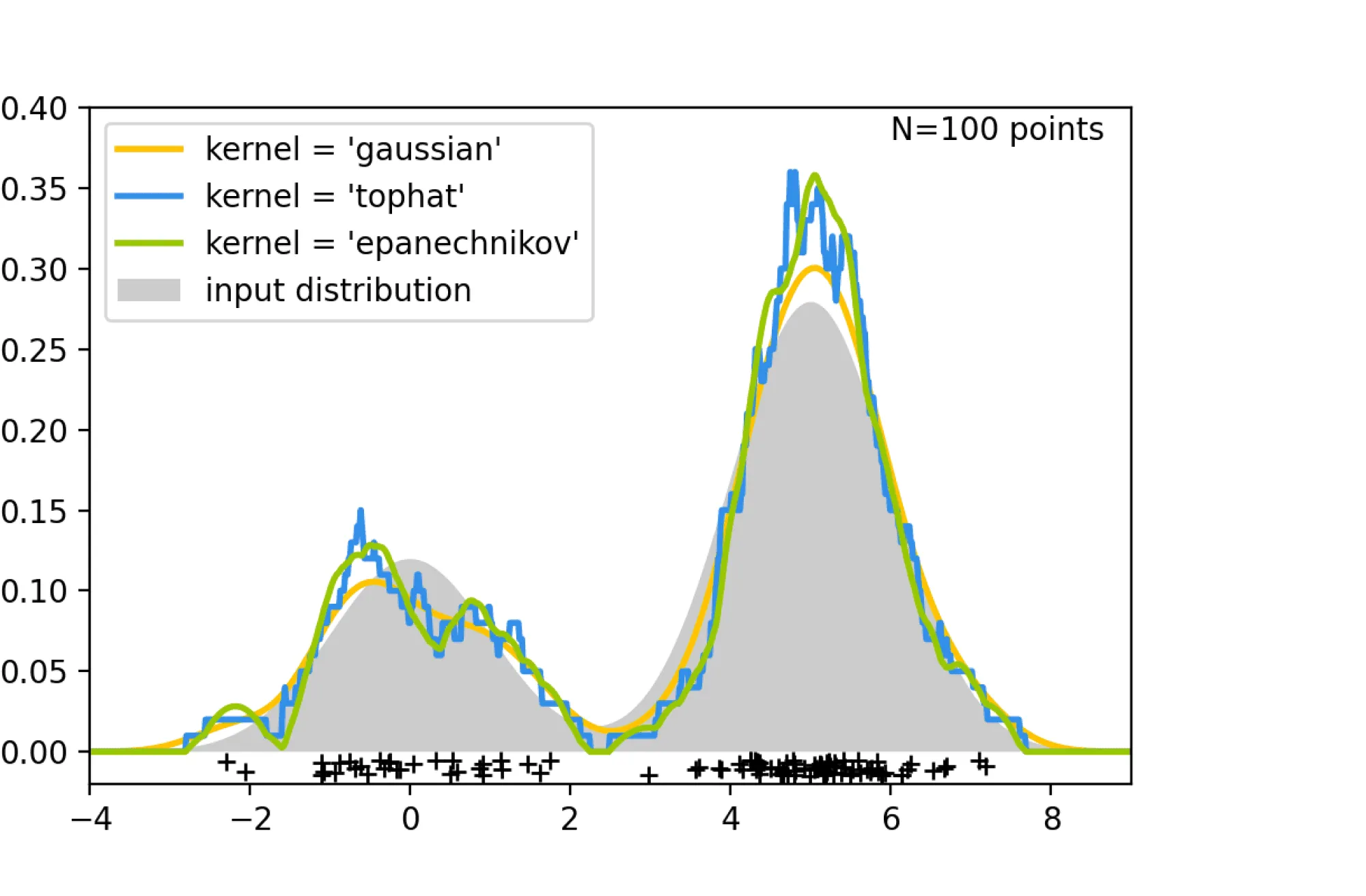
Результат оценки плотности с разными ядрами. Использованы изображения из:
При параметрической оценке плотности предполагают, что искомое распределение лежит в параметризованном классе, и подбирают значения параметров при помощи метода максимума правдоподобия. Например, предположим, что искомое распределение нормальное. Тогда функция его плотности имеет вид
Таким образом, чтобы оценить плотность , достаточно оценить параметры . Метод максимума правдоподобия в этом случае даст такие оценки:
— выборочное среднее, — выборочное стандартное отклонение.
Если в модели NB распределения всех признаков объектов каждого класса нормальные, оценив параметры этих распределений, мы сможем каждый класс описать нормальным распределением со средним и диагональной ковариационной матрицей, значения на диагонали которой обозначим .
Таким образом, полученная модель (Gaussian Naive Bayes, GNB) эквивалентна модели GDA с дополнительным ограничением на диагональность ковариационных матриц.
Наивный байесовский подход и логистическая регрессия
Предположим теперь, что в модели GNB класса всего 2, причём соответствующие им ковариационные матрицы совпадают, как это было в модели LDA. Таким образом .
Посмотрим, как будет выглядеть в этом случае. По теореме Байеса имеем
Разделим числитель и знаменатель полученного выражения на числитель:
Из условной независимости относительно получаем
Перепишем сумму в знаменателе, воспользовавшись формулой плотности нормального распределения
Подставляя это выражение в формулу (5) , получаем
Таким образом, представляется в GNB с общей ковариационной матрицей в таком же виде, как в модели логистической регрессии:
где в случае GNB
Однако это не значит, что модели эквивалентны: модель логистической регрессии накладывает менее строгие ограничения на распределение , чем GNB.
Так, могут не являться условно независимыми относительно , а распределения могут не удовлетворять нормальному закону, но может при этом всё равно представляться в виде формулы (6) .
В этом случае использование метода логистической регрессии предпочтительнее. С другой стороны, если есть основания полагать, что требования GNB выполняются, то от GNB можно ожидать более высокого качества классификации по сравнению с логистической регрессией.



