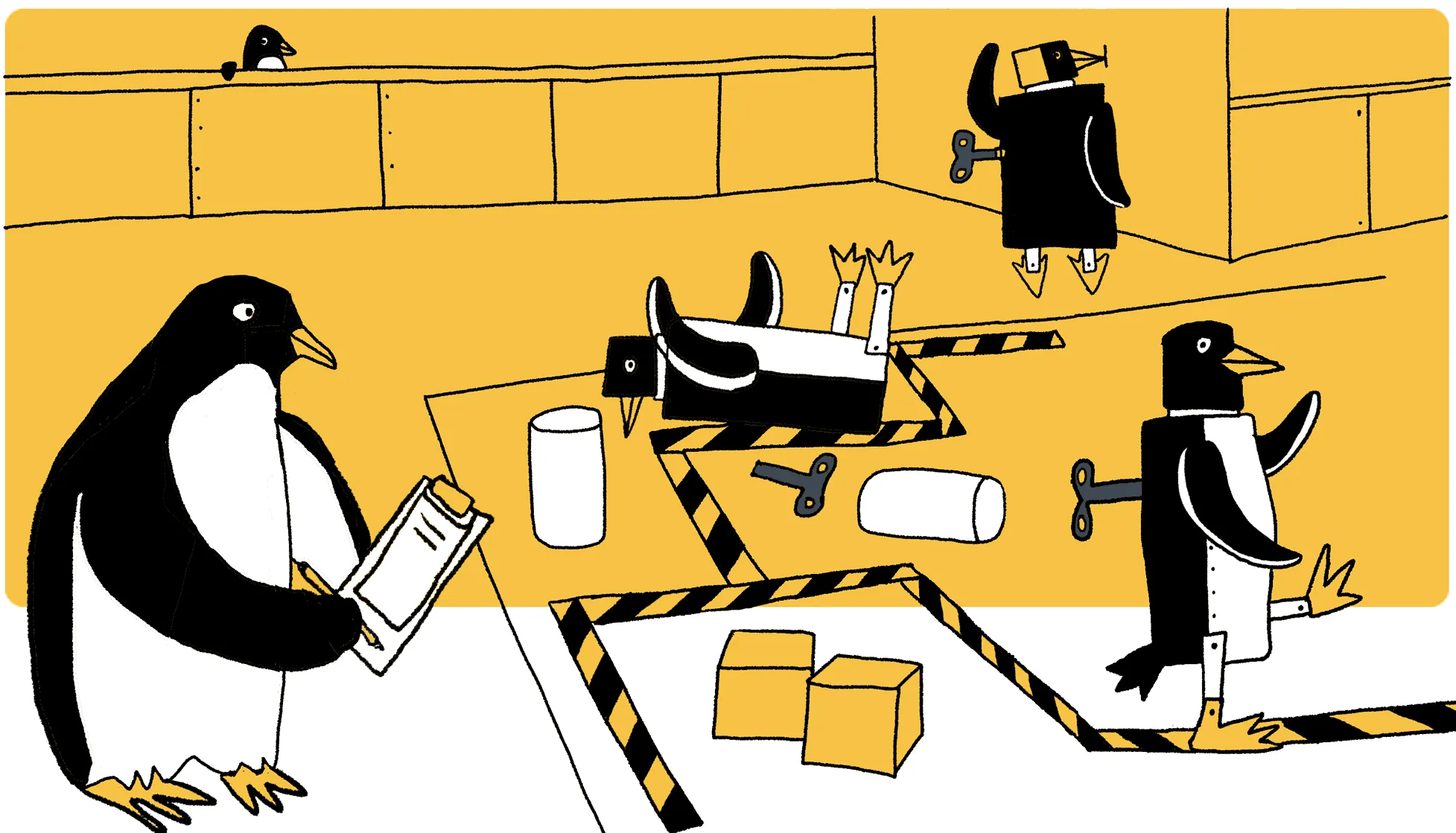
До сих пор опыт, благодаря которому было возможно обучение в наших алгоритмах, был задан в виде обучающей выборки. Насколько такая модель обучения соотносится с тем, как учится, например, человек? Чтобы научиться кататься на велосипеде, печь тортики или играть в теннис, нам не нужны огромные датасеты с примерами того, что нужно делать в каждый момент; вместо этого мы способны обучаться методом проб и ошибок (trial and error), предпринимая попытки решить задачу, взаимодействуя с окружающим миром, и как-то улучшая своё поведение на основе полученного в ходе этого взаимодействия опыта.
В обучении с подкреплением (reinforcement learning, RL) мы хотим построить алгоритм, моделирующий обучение методом проб и ошибок. Вместо получения обучающей выборки на вход такой алгоритм будет взаимодействовать с некоторой средой (environment), окружающим миром, а в роли «разметки» будет выступать награда (reward) — скалярная величина, которая выдаётся после каждого шага взаимодействия со средой и показывает, насколько хорошо алгоритм справляется с поставленной ему задачей. Например, если вы печёте тортики, то за каждый испечённый тортик вы получаете +1, а если вы пытаетесь кататься на велосипеде, то за каждое падение с велосипеда вам прилетает -1.
- Награда не подсказывает, как именно нужно решать задачу и что вообще нужно делать;
- Награда может быть отложенной во времени (вы нашли в пустыне сокровища, но чтобы получить заслуженные тортики, вам ещё понадобится куча времени, чтобы выбраться из пустыни; а награда приходит только за тортики) или сильно разреженной (большую часть времени давать агенту +0). Всё это сильно отличает задачу от обучения с учителем;
- Награда предоставляет какой-то «сигнал» для обучения (хорошо/плохо), которого нет, например, в обучении без учителя.

источник картинки — курс UC Berkeley AI
Постановка задачи
Теперь попробуем формализовать всю эту концепцию и познакомиться с местной терминологией. Задача обучения с подкреплением задаётся Марковским Процессом Принятия Решений (Markov Decision Process или сокращённо MDP) это четвёрка , где:
- — пространство состояний (state space), множество состояний, в которых в каждый момент времени может находиться среда.
- — пространство действий (action space), множество вариантов, из которых нужно производить выбор на каждом шаге своего взаимодействия со средой.
- — функция переходов (transition function), которая задаёт изменение среды после того, как в состоянии было выбрано действие . В общем случае функция переходов может быть стохастична, и тогда такая функция переходов моделируется распределением : с какой вероятностью в какое состояние перейдёт среда после выбора действия в состоянии .
- — функция награды (reward function), выдающая скалярную величину за выбор действия в состоянии . Это наш «обучающий сигнал».
Традиционно субъект, взаимодействующий со средой и влияющий на неё, называется в обучении с подкреплением агентом (agent). Агент руководствуется некоторым правилом, возможно, тоже стохастичным, как выбирать действия в зависимости от текущего состояния среды, которое называется стратегией (policy; термин часто транслитерируют и говорят политика) и моделируется распределением . Стратегия и будет нашим объектом поиска, поэтому, как и в классическом машинном обучении, мы ищем какую-то функцию.
Взаимодействие со средой агента со стратегией моделируется так. Изначально среда находится в некотором состоянии . Агент сэмплирует действие из своей стратегии . Среда отвечает на это, сэмплируя своё следующее состояние из функции переходов, а также выдаёт агенту награду в размере . Процесс повторяется: агент снова сэмплирует , а среда отвечает генерацией и скалярной наградой . Так продолжается до бесконечности или пока среда не перейдёт в терминальное состояние, после попадания в которое взаимодействие прерывается, и сбор агентом награды заканчивается. Если в среде есть терминальные состояния, одна итерация взаимодействия от начального состояния до попадания в терминальное состояние называется эпизодом (episode). Цепочка генерируемых в ходе взаимодействия случайных величин называется траекторией (trajectory). Примечание: функция награды тоже может быть стохастичной, и тогда награды за шаг тоже будут случайными величинами и частью траекторий, но без ограничения общности мы будем рассматривать детерминированные функции награды.

Итак, фактически среда для нас — это управляемая марковская цепь: на каждом шаге мы выбором определяем то распределение, из которого будет генерироваться следующее состояние. Мы предполагаем, во-первых, марковское свойство: что переход в следующее состояние определяется лишь текущим состоянием и не зависит от всей предыдущей истории:
Во-вторых, мы предполагаем стационарность: функция переходов не зависит от времени, от того, сколько шагов прошло с начала взаимодействия. Это довольно реалистичные предположения: законы мира не изменяются со временем (стационарность), а состояние — описывает мир целиком (марковость). В этой модели взаимодействия есть только одно нереалистичное допущение: полная наблюдаемость (full observability), которая гласит, что агент в своей стратегии наблюдает всё состояние полностью и может выбирать действия, зная об окружающем мире абсолютно всё; в реальности нам же доступны лишь какие-то частичные наблюдения состояния. Такая более реалистичная ситуация моделируется в частично наблюдаемых MDP (Partially observable MDP, PoMDP), но мы далее ограничимся полностью наблюдаемыми средами.
Итак, мы научились на математическом языке моделировать среду, агента и их взаимодействие между собой. Осталось понять, чего же мы хотим. Во время взаимодействия на каждом шаге агенту приходит награда , однако, состояния и действия в рамках такой постановки — случайные величины. Один и тот же агент может в силу стохастики как внутренней (в силу случайности выбора действий в его стратегии), так и внешней (в силу стохастики в функции переходов) набирать очень разную суммарную награду в зависимости от везения. Мы скажем, что хотим научиться выбирать действия так, чтобы собирать в среднем как можно больше награды.
Что значит в среднем, в среднем по чему? По всей стохастике, которая заложена в нашем процессе взаимодействия со средой. Каждая стратегия задаёт распределение в пространстве траекторий — с какой вероятностью нам может встретится траектория :
Вот по такому распределению мы и хотим взять среднее получаемой агентом награды. Записывают это обычно как-нибудь так:
Здесь мат.ожидание по траекториям — это бесконечная цепочка вложенных мат.ожиданий:
Вот такую конструкцию мы и хотим оптимизировать выбором стратегии . На практике, однако, вносят ещё одну маленькую корректировку. В средах, где взаимодействие может продолжаться бесконечно долго, агент может научиться набирать бесконечную награду, с чем могут быть связаны разные парадоксы (например, получать +1 на каждом втором шаге становится также хорошо, как получать +1 на каждом сотом шаге). Поэтому вводят дисконтирование (discounting) награды, которое гласит: тортик сейчас лучше, чем тот же самый тортик завтра. Награду, которую мы получим в будущем, агент будет дисконтировать на некоторое число , меньшее единицы. Тогда наш функционал примет такой вид:
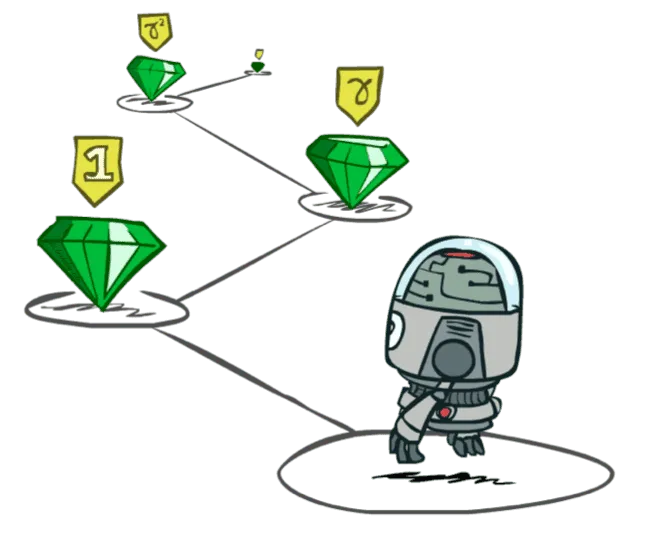
источник картинки — курс UC Berkeley AI
Заметим, что обучение с подкреплением - это в первую очередь задача оптимизации, оптимизации функционалов определённого вида. Если в классическом машинном обучении подбор функции потерь можно считать элементом инженерной части решения, то здесь функция награды задана нам готовая и определяет тот функционал, который мы хотим оптимизировать.
Примеры
Формализм MDP очень общий, и под него попадает практически всё, что можно назвать «интеллектуальной задачей» (с той оговоркой, что не всегда очевидно, какая функция награды задаёт ту или иную задачу).
Самые простые примеры MDP можно нарисовать «на бумажке». Например, часто рассматривают «клетчатые миры» (GridWorlds): агент находится в некоторой позиции клетчатой доски и может в качестве действий выбирать одно из четырёх направлений. Такие миры могут по-разному реагировать агента за выбор действия «пойти в стену», с некоторой вероятностью перемещать агента не в том направлении, которое он выбрал, содержать предметы в некоторых клетках и так далее. Пространство состояний, в которых может оказаться агент, в таких примерах конечно, как и пространство действий. Такие MDP называют табличными: все состояния и действия можно перечислить.
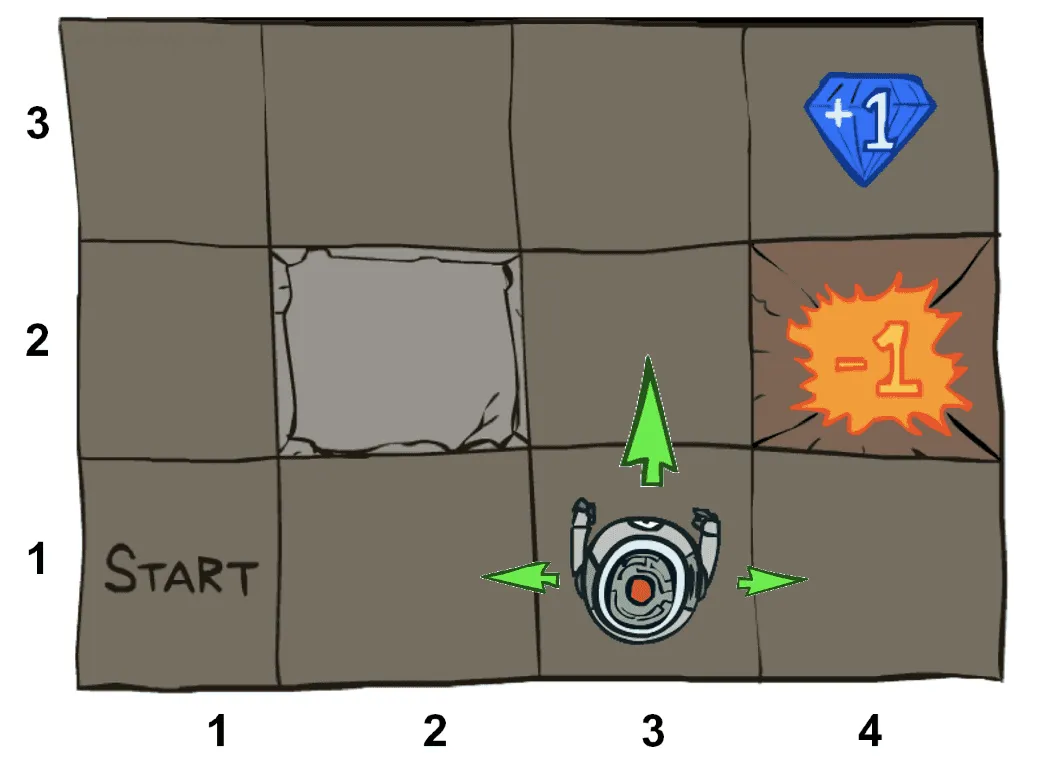
источник картинки — курс UC Berkeley AI
Огромное разнообразие MDP предоставляют видеоигры. Можно считать, что на вход агенту подаётся изображение экрана видеоигры, и несколько раз в секунду агент выбирает, какие кнопки на контроллере он хочет нажать. Тогда пространство состояний - множество всевозможных картинок, которые вам может показать видеоигра. Множество, в общем-то, конечное (конечное количество пикселей экрана с тремя цветовыми каналами, каждый из который показывает целочисленное значение от 0 до 255), но только очень большое; например, их уже нельзя перечислить или сохранить все возможные варианты в памяти. Но на каждом шаге нужно выбирать действие из конечного набора: какие кнопки нажать, поэтому это задачи дискретного управления.
источник картинки — курс UC Berkeley AI
Наконец, естественный способ создавать среды — использование физических симуляций. В качестве бенчмарка часто используют locomotion — задачу научить какое-нибудь «существо» ходить в рамках той или иной физической модели (примеры можно посмотреть, например, здесь). Причём концептуально, в рамках задачи обучения с подкреплением, нам даже неважно, как именно устроена симуляция или как задана функция награды: мы хотим построить общий алгоритм оптимизации этой самой награды. Если награда поощряет перемещение центра масс «существа» вдоль некоторого направления, агент постепенно научится выбирать действия так, чтобы существо перемещалось и не падало, если последнее приводит к завершению эпизода и мешает дальнейшему получению награды.

источник картинки — статья DeepMind Producing Flexible Behaviours in Simulated Environments
В таких задачах агент на каждом шаге выбирает несколько вещественных чисел в диапазоне , где -1 — «максимально расслабить» сустав, а +1 — «максимально напрячь». Такое пространство действий возникает во многих задачах робототехники, где нужно научиться поворачивать какой-нибудь руль, и у него есть крайнее правое и крайнее левое положение, но можно выбрать и любое промежуточное. Такие задачи называются задачами непрерывного управления (continuous control).
Окей, и как такое решать?
Выглядит сложновато, но у человечества есть уже довольно много наработок, как подойти к этой на вид очень общей задаче, причём с основной идеей вы скорее всего уже сталкивались. Называется она динамическим программированием.
Дело в том, что мы оптимизируем не абы какой функционал, а среднюю дисконтированную кумулятивную награду. Чтобы придумать более эффективное решение, чем какой-нибудь подход, не использующий этот факт (например, эволюционные алгоритмы), нам нужно воспользоваться структурой поставленной задачи. Эта структура задана в формализме MDP и определении процесса взаимодействия агента со средой. Интуитивно она выражается так: вот мы сидим в некотором состоянии и хотим выбрать действие как можно оптимальнее. Мы знаем, что после выбора этого действия мы получим награду за этот шаг , среда перекинет нас в состояние и, внимание, дальше нас ждёт подзадача эквивалентной структуры: в точности та же задача выбора оптимального действия, только в другом состоянии. Действительно: когда мы будем принимать решение на следующем шаге, на прошлое мы повлиять уже не способны; стационарность означает, что законы, по которым ведёт себя среда, не поменялись, а марковость говорит, что история не влияет на дальнейший процесс нашего взаимодействия. Это наводит на мысль, что задача максимизации награды из текущего состояния тесно связана с задачей максимизации награды из следующего состояния , каким бы оно ни было.
Чтобы сформулировать это на языке математики, вводятся «дополнительные переменные», вспомогательные величины, называемые оценочными функциями. Познакомимся с одной такой оценочной функцией - оптимальной Q-функцией, которую будем обозначать . Скажем, что - это то, сколько максимально награды можно (в среднем) набрать после выбора действия из состояния . Итак:
Запись здесь означает, что мы садимся в состояние ; выбираем действие , а затем продолжаем взаимодействие со средой при помощи стратегии , порождая таким образом траекторию . По определению, чтобы посчитать , нужно перебрать все стратегии, посмотреть, сколько каждая из них набирает награды после выбора из состояния , и взять наилучшую стратегию. Поэтому эта оценочная функция называется оптимальной: она предполагает, что в будущем после выбора действия из состояния агент будет вести себя оптимально.
Определение неконструктивное, конечно, поскольку в реальности мы так сделать не можем, зато обладает интересным свойством. Если мы каким-то чудом узнали , то мы знаем оптимальную стратегию. Действительно: представьте, что вы находитесь в состоянии , вам нужно сделать выбор из трёх действий, и вы знаете значения . Вы знаете, что если выберете первое действие , то в будущем сможете набрать не более чем, допустим, награды. При этом вы знаете, что существует какая-то стратегия , на которой достигается максимум в определении оптимальной Q-функции, то есть которая действительно позволяет набрать эти +3. Вы знаете, что если выберете второе действие, то в будущем сможете набрать, допустим, , а для третьего действия . Вопрос: так как нужно действовать? Интуиция подсказывает, что надо просто выбирать действие , что позволит набрать +10, ведь по определению больше набрать никак не получится. Значит, выбор в этом состоянии действия оптимален. Эта интуиция нас не обманывает, и принцип такого выбора называется принципом оптимальности Беллмана.
Выбор того действия, на котором достигается максимум по действиям Q-функции, называется жадным (greedy) по отношению к ней. Таким образом, принцип оптимальности Беллмана гласит:
жадный выбор по отношению к оптимальной Q-функции оптимален:
Примечание: если Q-функция достигает максимума на нескольких действиях, то можно выбирать любое из них.
Заметим, что эта оптимальная стратегия детерминирована. Этот интересный факт означает, что нам, в общем-то, необязательно искать стохастичную стратегию. Наше рассуждение пока даже показывает, что мы можем просто пытаться найти , а дальше выводить из неё оптимальную стратегию, выбирая действие жадно.
Но как искать ? Тут на сцене и появляется наше наблюдение про структуру задачи. Оказывается, выражается через саму себя. Действительно: рассмотрим некоторую пару состояние-действие . С одной стороны, по определению, мы в будущем сможем при условии оптимального поведения получить награды. С другой стороны, после того, как мы выберем действие в состоянии , мы получим награду за один шаг , вся дальнейшая награда будет дисконтирована на , среда ответит нам сэмплированием (на результат этого сэмплирования мы уже никак повлиять не можем и по этой стохастике нашу будущую награду надо будет усреднять), а затем в состоянии мы, в предположении оптимальности поведения, выберем то действие , на котором достигается максимум . Другими словами, в дальнейшем после попадания в мы сможем получить награды. А значит, верно следующее рекурсивное соотношение, называемое уравнением оптимальности Беллмана для Q-функции:
Мы получили систему уравнений, связывающую значения с самой собой. Это нелинейная система уравнений, но оказывается, что она в некотором смысле «хорошая». У неё единственное решение - и, значит, решение этого уравнения можно считать эквивалентным определением , - и его можно искать методом простой итерации. Метод простой итерации решения систем уравнений позволяет улучшать своё текущее приближение решения некоторого уравнения вида его подстановкой в правую часть. То есть: инициализируем произвольную функцию , которая будет приближать , затем итеративно будем подставлять её в правую часть уравнений оптимальности Беллмана и полученным значением обновлять наше приближение:
Такая процедура в пределе приведёт нас к истинной , а значит и оптимальной стратегии. Кстати, когда вы в прошлом встречались с динамическим программированием, вы скорее всего неявно использовали именно эту идею, разве что часто в задачах для решения уравнений оптимальности Беллмана можно просто последовательно исключать неизвестные переменные; но метод простой итерации даёт более общую схему, применимую всегда. А сейчас для нас принципиально следующее: если у нас есть какое-то приближение , то вычисление правой части уравнения оптимальности Беллмана позволит получить приближение лучше.
А где же метод проб и ошибок?
Решать методом простой итерации уравнения оптимальности Беллмана и таким образом получать в реальности можно только при двух очень существенных ограничивающих условиях. Нужно, чтобы, во-первых, мы могли хранить как-то текущее приближение в памяти. Это возможно только если пространства состояний и действий конечные и не очень большие, то есть, например, в вашем MDP всего 10 состояний и 5 действий, тогда — это табличка 10x5. Но что, если вы хотите научиться играть в видеоигру, и состояние — это входное изображение? Тогда множество картинок, которые вам может показать видеоигра, сохранить в памяти уже не получится. Ну, допустим пока, что число состояний и число действий не очень большое, и мы всё-таки можем хранить таблицу в памяти, а позже мы снимем это ограничение, моделируя при помощи нейросети.
Во-вторых, нам необходимо уметь считать выражение, стоящее справа в уравнение оптимальности Беллмана:
Мало того, что в сложных средах взять мат.ожидание по функции переходов в реальности мы не сможем, так ещё и обычно мы эту функцию переходов на самом деле не знаем. Представьте, что вы катаетесь на велосипеде: можете ли вы по текущему состоянию окружающего мира, например, положению всех атомов во вселенной, рассказать, с какими вероятностями в каком состоянии мир окажется в следующий момент времени? Это соображение также подсказывает, что было бы здорово, если б мы смогли решать задачу, избегая даже попыток выучить эту сложную функцию переходов.
Что нам доступно? Мы можем взять какую-нибудь стратегию (важный момент: мы должны сами выбрать какую) и повзаимодействовать ею со средой. «Попробовать решить задачу». Мы можем сгенерировать при помощи целую траекторию или даже сделать всего один шаг в среде. Таким образом мы соберём данные: допустим, мы были в состоянии и сделали выбор действия , тогда мы узнаем, какую награду мы получаем за такой шаг и, самое главное, в какое состояние нас перевела среда. Полученный — сэмпл из функции переходов . Собранная так информация — четвёрка — называется переходом (transition), и может быть как-то использована для оптимизации нашей стратегии.
Можем ли мы, используя лишь переходы , то есть имея на руках лишь сэмплы , как-то пользоваться схемой динамического программирования? Что, если мы будем заменять значение не на
которое мы не можем посчитать, а на его Монте Карло оценку:
где — сэмпл из функции переходов из собранного нами опыта? В среднем-то такая замена верная. Такая Монте-Карло оценка правой части для заданного переходика называется Беллмановским таргетом, то есть «целевой переменной». Почему такое название — мы увидим чуть позже.
Чтобы понять, как нам нужно действовать, рассмотрим какую-нибудь типичную ситуацию. Допустим, после выполнения действия из некоторого состояния среда награждает нас и перекидывает нас с равными вероятностями то в состояние , для которого , то в состояние , для которого . Метод простой итерации говорит, что на очередной итерации нужно заменить на , но в реальности мы встретимся лишь с одним исходом, и таргет — Монте-Карло оценка правой части уравнения оптимальности Беллмана — будет с вероятностью 0.5 равен , а с вероятностью 0.5 равен . Ясно, что нельзя просто взять и жёстко заменять наше текущее приближение на посчитанный Беллмановский таргет по некоторому одному переходу, поскольку нам могло повезти (мы увидели ) или не повезти (мы увидели ). Давайте вместо этого поступать также, как учат среднее по выборке: не сдвигать «жёстко» наше текущее приближение в значение очередного сэмпла, а смешивать текущее приближение с очередным сэмплом. То есть: берём переходик , и не заменяем на стохастичную оценку правой части уравнения оптимальности Беллмана, а только сдвигаемся в его сторону:
Таким образом, мы проводим экспоненциальное сглаживание старого приближения и новой оценки правой части уравнения оптимальности Беллмана со свежим сэмплом . Выбор здесь определяет, насколько сильно мы обращаем внимание на последние сэмплы, и имеет тот же физический смысл, что и learning rate. В среднем по стохастике (а стохастика в этой формуле обновления заложена в случайном ) мы будем сдвигаться в сторону
и значит применять этакий «зашумлённый» метод простой итерации.
Итак, возникает следующая идея. Будем как-то взаимодействовать со средой и собирать переходики . Для каждого перехода будем обновлять одну ячейку нашей Q-таблицы размера число состояний на число действий по вышеуказанной формуле. Таким образом мы получим как бы «зашумлённый» метод простой итерации, где мы на каждом шаге обновляем только одну ячейку таблицы, и не заменяем жёстко значение на правую часть уравнений оптимальности, а лишь сдвигаемся по некоторому в среднем верному стохастичному направлению.
Очень похоже на стохастическую оптимизацию вроде стохастического градиентного спуска, и поэтому гарантии сходимости выглядят схожим образом. Оказывается, такой алгоритм сходится к истинной , если для любой пары мы в ходе всего процесса проводим бесконечное количество обновлений, а learning rate (гиперпараметр ) в них ведёт себя как learning rate из условий сходимости стохастического градиентного спуска:
Пример
Колобок Колабулька любит играть в лотереи. Допустим, в некотором состоянии он выполнил действие «купить билет» и предполагает, что в будущем сможет набрать награды. Однако, за покупку билета он платит 10 долларов, и таким образом теряет 10 награды на данном шаге , при этом попадая в состояние , где ему снова предлагается купить билет в лотерею (он может выбрать действие «купить» или действие «не купить»). Ну, допустим, текущая оценка Колабульки будущей награды в случае отказа купить билет равна 0 < +100, поэтому колобок предполагает, что в будущем из состояния он сможет получить . Для простоты допустим . Тогда получается, что одношаговое приближение будущей награды . Да, здесь — случайная величина, колобку могло повезти или не повезти (и мы, увидев всего один сэмпл из функции переходов, не можем сказать наверняка, повезло ли нам сейчас или нет), но наша формула говорит сдвинуть аппроксимацию в сторону Беллмановского таргета.

Допустим, learning rate : тогда, сдвигая +100 в сторону +90, ожидания от будущей награды после покупки лотерейного билета опускаются до 95. Всё ещё , поэтому колобку кажется, что покупать билет выгоднее, чем не покупать, поэтому рассмотрим следующий переходик. Допустим, колобок снова купил билет, снова потерял 10 долларов и снова попал в то же самое . Наше обновление снова скажет уменьшать значение :

Видно, что если колобку продолжит так не везти, таргет будет всё время на 10 меньше, чем текущее приближение, и будет всё уменьшаться и уменьшаться, пока не свалится до нуля (а там будет выгоднее уже не покупать билет). Но если на очередной итерации Колабульке повезло, и среда перевела его в , соответствующее победе в лотерею (а это, видимо, происходит с какой-то маленькой вероятностью), таргет получится очень большим, и аппроксимацию наше обновление скажет сильно увеличить:

Куда будет сходиться такой алгоритм? Давайте предположим, что среда на покупку лотерейного билета отвечает с вероятностью возвращением в то же состояние , где колобку предлагается купить ещё один билет, а с вероятностью билет оказывается выигрышным, и колобок попадает в такое состояние , в котором он может забрать приз и получить +1000 (после этого взаимодействие со средой, скажем, заканчивается). Давайте запишем уравнение оптимальности Беллмана для действия «купить билет» в состоянии :
Здесь , поскольку колобок может или покупать билет, или не покупать (это, допустим, принесёт ему 0 награды). Понятно, что если покупка билета не принесёт больше 0 награды, то не имеет смысла его покупать. Подставляя все числа из примера, получаем:
Видно, что если вероятность проигрыша в лотерею , то решением уравнения является : Колабулька платит за билет 10 долларов и получает 1000 награды с вероятностью 0.01. В этом случае действие «купить билет» и «не покупать» равноценны, и оба в будущем принесут в среднем 0 награды. Если же , то покупать билет становится невыгодно, а если , то выгодно покупать билет до тех пор, пока не случится победа. Несмотря на то, что в таргете содержится собственная же текущая аппроксимация будущей награды и используется лишь один сэмпл вместо честного усреднения по всевозможным исходам, формула обновления постепенно сойдётся к этому решению. Причём колобку истинное значение неизвестно, и в формуле обновления эта вероятность влияла лишь на появление того или иного в очередном таргете.
Этот алгоритм, к которому мы уже практически пришли, называется Q-learning, «обучение оптимальной Q-функции». Нам, однако, осталось ответить на один вопрос: так как же нужно собирать данные, чтобы удовлетворить требованиям для сходимости? Как взаимодействовать со средой так, чтобы мы каждую ячейку не прекращали обновлять?
Дилемма Exploration-exploitation
Мы уже встречали дилемму exploration-exploitation (букв. «исследования-использования») в параграфе про тюнинг гиперпараметров. Задача многоруких бандитов, которая там встретилась, на самом деле является частным случаем задачи обучения с подкреплением, в котором после первого выбора действия эпизод гарантированно завершается, и этот частный случай задачи часто используется для изучения этой дилеммы. Рассмотрим эту дилемму в нашем контексте.
Допустим, на очередном шаге алгоритма у нас есть некоторое приближение . Приближение это, конечно, неточное, поскольку алгоритм, если и сходится к истинной оптимальной Q-функции, то на бесконечности. Как нужно взаимодействовать со средой? Если вы хотите набрать максимальную награду, наверное, стоит воспользоваться нашей теорией и заниматься exploitation-ом, выбирая действие жадно:
Увы, такой выбор не факт что совпадёт с истинной оптимальной стратегией, а главное, он детерминирован. Это значит, что при взаимодействии этой стратегией со средой, многие пары никогда не будут встречаться просто потому, что мы никогда не выбираем действие в состоянии . А тогда мы, получается, рискуем больше никогда не обновить ячейку для таких пар!
Такие ситуации запросто могут привести к застреванию алгоритма. Мы хотели научиться кататься на велосипеде и получали +0.1 за каждый пройденный метр и -5 за каждое попадание в дерево. После первых проб и ошибок мы обнаружили, что катание на велосипеде приносит нам -5, поскольку мы очень скоро врезаемся в деревья и обновляли нашу аппроксимацию Q-функции сэмплами с негативной наградой; зато если мы не будем даже забираться на велосипед и просто займёмся ничего не деланьем, то мы сможем избежать деревьев и будем получать 0. Просто из-за того, что в нашей стратегии взаимодействия со средой никогда не встречались те , которые приводят к положительной награде, и жадная стратегия по отношению к нашей текущей аппроксимации Q-функции никогда не выбирает их. Поэтому нам нужно экспериментировать и пробовать новые варианты.
Режим exploration-а предполагает, что мы взаимодействуем со средой при помощи какой-нибудь стохастичной стратегии . Например, такой стратегией является случайная стратегия, выбирающая рандомные действия. Как ни странно, сбор опыта при помощи случайной стратегии позволяет побывать с ненулевой вероятностью во всех областях пространства состояний, и теоретически даже наш алгоритм обучения Q-функции будет сходится. Означает ли это, что exploration-а хватит, и на exploitation можно забить?
В реальности мы понимаем, что добраться до самых интересных областей пространства состояний, где функция награда самая большая, не так-то просто, и случайная стратегия хоть и будет это делать с ненулевой вероятностью, но вероятность эта будет экспоненциально маленькая. А для сходимости нам нужно обновить ячейки для этих интересных состояний бесконечно много раз, то есть нам придётся дожидаться необычайно редкого везения далеко не один раз. Куда разумнее использовать уже имеющиеся знания и при помощи жадной стратегии, которая уже что-то умеет, идти к этим интересным состояниям. Поэтому для решения дилеммы exploration-exploitation обычно берут нашу текущую жадную стратегию и что-нибудь с ней делают такое, чтобы она стала чуть-чуть случайной. Например, с вероятностью выбирают случайное действие, а с вероятностью — жадное. Тогда мы чаще всё-таки и знаниями пользуемся, и любое действие с ненулевой вероятностью выбираем; такая стратегия называется -жадной, и она является самым простым способом как-то порешать эту дилемму.
Давайте закрепим, что у нас получилось, в виде табличного алгоритма обучения с подкреплением под названием Q-learning:
- Проинициализировать произвольным образом.
- Пронаблюдать из среды.
- Для :
- с вероятностью выбрать действие случайно, иначе жадно:
- отправить действие в среду, получить награду за шаг и следующее состояние
. - обновить одну ячейку таблицы:
Добавим нейросеток
Наконец, чтобы перейти к алгоритмам, способным на обучение в сложных MDP со сложным пространством состояний, нужно объединять классическую теорию обучения с подкреплением с парадигмами глубокого обучения.
Допустим, мы не можем позволить себе хранить как таблицу в памяти, например, если мы играем в видеоигру и на вход нам подаются какие-нибудь изображения. Тогда мы можем обрабатывать любые имеющиеся у агента входные сигналы при помощи нейросетки . Для тех же видеоигр мы легко обработаем изображение экрана небольшой свёрточной сеточкой и выдадим для каждого возможного действия вещественный скаляр . Допустим также, что пространство действий всё ещё конечное и маленькое, чтобы мы могли для такой модели строить жадную стратегию, выбирать . Но как обучать такую нейросетку?
Давайте ещё раз посмотрим на формулу обновления в Q-learning для одного переходика :
Теория Q-learning-а подсказывала, что у процесса такого обучения Q-функции много общего с обычным стохастическим градиентным спуском. В таком виде формула подсказывает, что, видимо,
— это стохастическая оценка какого-то градиента. Этот градиент сравнивает Беллмановский таргет
с нашим текущим приближением и чуть-чуть корректирует это значение, сдвигая в сторону таргета. Попробуем «заменить» в этой формуле Q-функцию с табличного представления на нейросетку.
Рассмотрим такую задачу регрессии. Чтобы построить один прецедент для обучающей выборки, возьмём один имеющийся у нас переходик . Входом будет пара . Целевой переменной, таргетом, будет Беллмановский таргет
его зависимость от параметров нашей нейронки мы далее будем игнорировать и будем «притворяться», что это и есть наш ground truth. Именно поэтому Монте-Карло оценка правой части уравнения оптимальности Беллмана и называют таргетом. Но важно помнить, что эта целевая переменная на самом деле «зашумлена»: в формуле используется взятый из перехода , который есть лишь сэмпл из функции переходов. На самом же деле мы хотели бы выучить среднее значение такой целевой переменной, и поэтому в качестве функции потерь мы возьмём MSE. Как будет выглядеть шаг стохастического градиентного спуска для решения этой задачи регрессии (для простоты — для одного прецедента)?
Это практически в точности повторяет формулу Q-learning, которая гласит, что если таргет больше , то нужно подстроить веса нашей модели так, чтобы стало чуть побольше, и наоборот. В среднем при такой оптимизации мы будем двигаться в сторону
— в сторону правой части уравнения оптимальности Беллмана, то есть моделировать метод простой итерации для решения системы нелинейных уравнений.
Единственное отличие такой задачи регрессии от тех, с которыми сталкивается традиционное глубокое обучение — то, что целевая переменная зависит от нашей же собственной модели. Раньше целевые переменные были напрямую источником обучающего сигнала. Теперь же, когда мы хотим выучить будущую награду при условии оптимального поведения, мы не знаем этого истинного значения или даже её стохастичных оценок. Поэтому мы применяем идею бутстрапирования (bootstrapping): берём награду за следующий шаг, и нечестно приближаем всю остальную награду нашей же текущей аппроксимацией . Да, за этим кроется идея метода простой итерации, но важно понимать, что такая целевая переменная лишь указывает направление для обучения, но не является истинным приближением будущих наград или даже их несмещённой оценкой. Поэтому говорят, что в этой задаче регрессии очень смещённые (biased) целевые переменные.
На практике из-за этого возникает беда. Наша задача регрессии в таком виде меняется после каждого же шага. Если вдруг после очередного шага оптимизации и обновления весов нейросети наша модель начала выдавать какие-то немного неадекватные значения, они рискуют попасть в целевую переменную на следующем шаге, мы сделаем шаг обучения под неадекватные целевые переменные, модель станет ещё хуже, и так далее, начнётся цепная реакция. Алгоритмы, в которых целевая переменная вот так напрямую зависит от текущей же модели, из-за этого страшно нестабильны.
Для стабилизации применяется трюк, называемый таргет-сетью (target network). Давайте сделаем так, чтобы у нас задача регрессии менялась не после каждого обновления весов нейросетки, а хотя бы раз, скажем, в 1000 шагов оптимизации. Для этого заведём полную копию нашей нейросети («таргет-сеть»), веса которой будем обозначать . Каждые 1000 шагов будем копировать веса из нашей модели в таргет-сеть , больше никак менять не будем. Когда мы захотим для очередного перехода построить таргет, мы воспользуемся не нашей свежей моделью, а таргет-сетью:
Тогда правило, по которому строится целевая переменная, будет меняться раз в 1000 шагов, и мы 1000 шагов будем решать одну и ту же задачу регрессии. Такой процесс будет намного стабильнее.
Experience Replay
Чтобы окончательно собрать алгоритм Deep Q-learning (обычно называемый DQN, Deep Q-network), нам понадобится сделать последний шаг, связанный опять со сбором данных. Коли мы хотим обучать нейросетку, нам нужно для каждого обновления весов откуда-то взять целый мини-батч данных, то есть батч переходов , чтобы по нему усреднить оценку градиента. Однако, если мы возьмём среду, сделаем в ней шагов, то встреченные нами переходов будут очень похожи друг на друга: они все придут из одной и той же области пространства состояний. Обучение нейросетки на скоррелированных данных — плохая идея, поскольку такая модель быстро забудет, что она учила на прошлых итерациях.
Бороться с этой проблемой можно двумя способами. Первый способ, доступный всегда, когда среда задана при помощи виртуального симулятора — запуск параллельных агентов. Запускается параллельно процессов взаимодействия агента со средой, и для того, чтобы собрать очередной мини-батч переходов для обучения, во всех экземплярах проводится по одному шагу взаимодействия, собирается по одному переходику. Такой мини-батч уже будет разнообразным.
Более интересный второй способ. Давайте после очередного шага взаимодействия со средой мы не будем тут же использовать переход для обновления модели, а запомним этот переход и положим его себе в коллекцию. Память со всеми встретившимися в ходе проб и ошибок переходами называется реплей буфером (replay buffer или experience replay). Теперь для того, чтобы обновить веса нашей сети, мы возьмём и случайно засэмплируем из равномерного распределения желаемое количество переходов из всей истории.
Однако, использование реплей буфера возможно далеко не во всех алгоритмах обучения с подкреплением. Дело в том, что некоторые алгоритмы обучения с подкреплением требуют, чтобы данные для очередного шага обновления весов были сгенерированы именно текущей, самой свежей версией стратегии. Такие алгоритмы относят к классу on-policy: они могут улучшать стратегию только по данным из неё же самой («on policy»). Примером on-policy алгоритмов выступают, например, эволюционные алгоритмы. Как они устроены: например, можно завести популяцию стратегий, поиграть каждой со средой, отобрать лучшие и как-то породить новую популяцию (подробнее про одну из самых успешных схем в рамках такой идеи можно посмотреть здесь). Как бы ни была устроена эта схема, эволюционный алгоритм никак не может использовать данные из, например, старых, плохих стратегий, которые вели себя, скажем, не сильно лучше случайной стратегии. Поэтому неизбежно в эволюционном подходе нужно свежую популяцию отправлять в среду и собирать новые данные перед каждым следующим шагом.
И вот важный момент: Deep Q-learning, как и обычный Q-learning, относится к off-policy алгоритмам обучения с подкреплением. Совершенно неважно, какая стратегия, умная или не очень, старая или новая, породила переход , нам всё равно нужно решать уравнение оптимальности Беллмана в том числе и для этой пары и нам достаточно при построении таргета лишь чтобы был сэмплом из функции переходов (а она-то как раз одна вне зависимости от того, какая стратегия взаимодействует в среде). Поэтому обновлять модель мы можем по совершенно произвольному опыту, и, значит, мы в том числе можем использовать experience replay.
источник картинки — курс UC Berkeley AI
В любом случае, даже в сложных средах, при взаимодействии со средой мы всё равно должны как-то разрешить дилемму exploration-exploitation, и пользоваться, например, -жадной стратегией исследования. Итак, алгоритм DQN выглядит так:
- Проинициализировать нейросеть .
- Проинициализировать таргет-сеть, положив .
- Пронаблюдать из среды.
- Для :
- с вероятностью выбрать действие случайно, иначе жадно:
- отправить действие в среду, получить награду за шаг и следующее состояние
. - добавить переход в реплей буфер.
- если в реплей буфере скопилось достаточное число переходиков, провести шаг обучения. Для этого сэмплируем мини-батч переходиков из буфера.
- для каждого переходика считаем целевую переменную:
- сделать шаг градиентного спуска для обновления , минимизируя
- если делится на 1000, обновить таргет-сеть: .
Алгоритм DQN не требует никаких handcrafted признаков или специфических настроек под заданную игру. Один и тот же алгоритм, с одними и теми же гиперпараметрами, можно запустить на любой из 57 игр древней консоли Atari (пример игры в Breakout) и получить какую-то стратегию. Для сравнения алгоритмов RL между собой результаты обычно усредняют по всем 57 играм Atari. Недавно алгоритм под названием Agent57, объединяющий довольно много модификаций и улучшений DQN и развивающий эту идею, смог победить человека сразу во всех этих 57 играх.
А если пространство действий непрерывно?
Всюду в DQN мы предполагали, что пространство действий дискретно и маленькое, чтобы мы могли считать жадную стратегию и считать максимум в формуле целевой переменной . Если пространство действий непрерывно, и на каждом шаге от агента ожидается выбор нескольких вещественных чисел, то как это делать непонятно. Такая ситуация повсюду возникает в робототехнике. Там каждое сочленение робота можно, например, поворачивать вправо / влево, и такие действия проще описывать набором чисел в диапазоне [-1, 1], где -1 — крайне левое положение, +1 — крайне правое, и доступны любые промежуточные варианты. При этом дискретизация действий не вариант из-за экспоненциального взрыва числа вариантов и потери семантики действий. Нам, в общем-то, нужно в DQN только одну проблему решить: как-то научиться аргмаксимум по действиям брать.
А давайте, коли мы не знаем , приблизим его другой нейросеткой. А то есть, заведём вторую нейросеть с параметрами , и будем учить её так, чтобы
Как это сделать? Ну, будем на каждой итерации алгоритма брать батч состояний из нашего реплей буфера и будем учить выдавать такие действия, на которых наша Q-функция выдаёт большие скалярные значения:
Причём, поскольку действия непрерывные, всё слева дифференцируемо и мы можем напрямую применять самый обычный backpropagation!
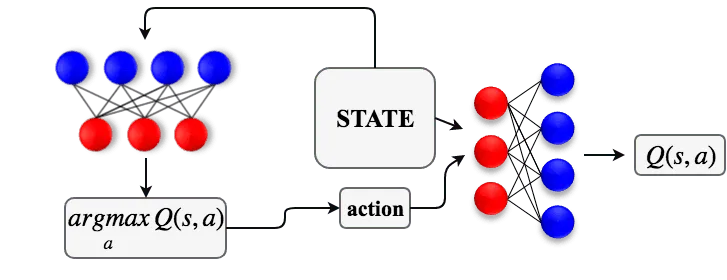
Теперь когда на руках есть приближение , можно просто использовать его всюду, где нам нужны аргмаксимумы и максимумы от нашей Q-функции. Мы получили Actor-Critic схему: у нас есть актёр, — детерминированная стратегия, и критик , который оценивает выбор действий актёром и предоставляет градиент для его улучшения. Актёр учится выбирать действия, которые больше всего нравятся критику, а критик учится регрессией с целевой переменной
Эта прикольная рабочая эвристика позволяет придумать off-policy алгоритмы для непрерывных пространств действий; к такому подходу относятся такие алгоритмы, как DDPG, TD3 и SAC.
Policy Gradient алгоритмы
В рассмотренных алгоритмах есть несколько приниципиальных ограничений, которые вытекают непосредственно из самой идеи подхода. Мы учимся с таргетов, заглядывающих всего на один шаг вперёд, использующих только ; это чревато проблемой накапливающейся ошибки, поскольку если между выполнением действия и получением награды +1 проходит 100 шагов, нам нужно на сто шагов «распространять» полученный сигнал. Мы должны учить вместо того, чтобы как-то напрямую («end-to-end») запомнить, какие действия в каких состояниях хорошие. Наконец, наша стратегия всегда детерминирована, когда для взаимодействия со средой во время сбора данных, например, нам позарез нужна была стохастичная, чтобы гарантированно обновлять Q-функцию для всех пар , и эту проблему пришлось закрывать костылями.
Есть второй подход model-free алгоритмов RL, называемый Policy Gradient, который позволяет избежать вышеперечисленных недостатков за счёт on-policy режима работы. Идея выглядит так: давайте будем искать стратегию в классе стохастичных стратегий, то есть заведём нейросеть, моделирующую напрямую. Тогда наш функционал, который мы оптимизируем,
дифференцируем по параметрам , и градиент равен:
где - reward-to-go с шага , то есть награда, собранная в сыгранном эпизоде после шага :
Скетч доказательства
Давайте распишем мат.ожидание по определению, как следующий интеграл:
где интеграл берётся по пространству всевозможных траекторий, — вероятность встретить траекторию при взаимодействии со средой стратегии , а — reward-to-go с шага , то есть суммарная дисконтированная награда за весь эпизод для рассматриваемой траектории . Награда от параметров не зависит; от выбора стратегии зависят лишь вероятности встретить ту или иную траекторию . Давайте пронесём градиент внутрь интеграла:
и теперь этот сложный интеграл перестал быть каким-то мат.ожиданием. Давайте исправим это при помощи трюка, который называется log-derivative trick: для этого домножим и поделим внутри на , получим:
Итак, мы увидели, что градиент нашего функционала — тоже мат.ожидание по всевозможным траекториям. Осталось заметить, что отношение градиента правдоподобия к значению правдоподобия — градиент логарифма правдоподобия:
(откуда и название трюка), чем мы и воспользуемся:
Вспоминая, как выглядит trajectory distribution для заданной стратегии , замечаем, что функция переходов в среде не вносит вклад в наш градиент:
Итого мы получили следующую формулу:
Отличие этой формулы от приведённой выше в том, что градиент, отвечающий за выбор действия в состоянии , взвешивается не на reward-to-go с момента времени , а на всю награду за эпизод, начиная с нулевого момента времени. Это странно, поскольку получается, что награда, собранная в прошлом, до принятия решения в момент времени , как-то влияет на градиент, соответствующий этому выбору. Мы же понимаем, что решение в момент времени на прошлую награду никак повлиять не могло, и странно, что градиент для решения в момент времени взвешивается на прошлую награду. Это наблюдение называется принципом причинности (causality principle); можно строго показать, что если заменить на , то «удалённые» таким образом слагаемые в среднем по траекториям дают нулевой вклад в градиент, и поэтому такая замена математически корректна.
Эта формула говорит нам, что градиент нашего функционала — это тоже мат.ожидание по траекториям. А значит, мы можем попробовать посчитать какую-то оценку этого градиента, заменив мат.ожидание на Монте Карло оценку, и просто начать оптимизировать наш функционал самым обычным стохастическим градиентным спуском! А то есть: берём нашу стратегию с текущими значениями параметров , играем эпизод (или несколько) в среде, то есть сэмплируем , и затем делаем шаг градиентного подъёма:
Почему эта идея приводит к on-policy подходу? Для каждого шага градиентного шага нам обязательно нужно взять с самыми свежими, с текущими весами , и никакая другая траектория, порождённая какой-то другой стратегией, нам не подойдёт. Поэтому для каждой итерации алгоритма нам придётся заново играть очередной эпизод со средой. Это sample-inefficient: неэффективно по числу сэмплов, мы собираем слишком много данных и очень неэффективно с ними работаем.
Policy Gradient алгоритмы пытаются по-разному бороться с этой неэффективностью, опять же обращаясь к теории оценочных функций и бутстрапированным оценкам, позволяющим предсказывать будущие награды, не доигрывая эпизоды целиком до конца. Большинство этих алгоритмов остаются в on-policy режиме и применимы в любых пространствах действий. К этим алгоритмам относятся такие алгоритмы, как Advantage Actor-Critic (A2C), Trust-Region Policy Optimization (TRPO) и Proximal Policy Optimization (PPO).
Что там ещё?
Мы до сих пор разбирали model-free алгоритмы RL, которые обходились без знаний о и никак не пытались приближать это распределение. Однако, в каких-нибудь пятнашках функция переходов нам известна: мы знаем, в какое состояние перейдёт среда, если мы выберем некоторое действие в таком-то состоянии. Понятно, что эту информацию было бы здорово как-то использовать. Существует обширный класс model-based, который либо предполагает, что функция переходов дана, либо мы учим её приближение, используя из нашего опыта в качестве обучающей выборки. Алгоритм AlphaZero на основе этого подхода превзошёл человека в игру Го, которая считалась куда более сложной игрой, чем шахматы; причём этот алгоритм возможно запустить обучаться на любой игре: как на Го, так и на шахматах или сёги.

источник картинки — курс UC Berkeley AI
Обучение с подкреплением стремится построить алгоритмы, способные обучаться решать любую задачу, представленную в формализме MDP. Как и обычные методы оптимизации, их можно использовать в виде чёрной коробочки из готовых библиотек, например, OpenAI Stable Baselines. Внутри таких коробочек будет, однако, довольно много гиперпараметров, которые пока не совсем понятно как настраивать под ту или иную практическую задачу. И хотя успехи Deep RL демонстрируют, что эти алгоритмы способны обучаться невероятно сложным задачам вроде победы над людьми в Dota 2 и в StarCraft II, они требуют для этого колоссального количества ресурсов. Поиск более эффективных процедур — открытая задача в Deep RL.
В ШАДе есть курс Practical RL, на котором вы погрузитесь глубже в мир глубокого обучения с подкреплением, разберётесь в более продвинутых алгоритмах и попробуете пообучать нейронки решать разные задачки в разных средах.