В этом параграфе вы познакомитесь с классической задачей, широко применяемой в анализе текстов, биоинформатике и других сферах. Вы узнаете, как находить минимальное количество операций (вставок, удалений и замен), чтобы превратить одну строку в другую, — и как вычислить это число эффективно с помощью динамического программирования.
Ключевые вопросы параграфа
- Что такое редакционное расстояние и как оно используется на практике?
- Как устроена рекурсивная формулировка задачи и почему мемоизация помогает?
- Как динамически находить расстояние между всеми префиксами двух строк?
- Как оптимизировать решение по памяти и находить выравнивание?

Варианты применения задачи
Есть множество вариантов, как применить задачу «Расстояние редактирования». Она подойдёт для обработки текстов на естественном языке, проверки правописания и других направлений. К примеру, биологи зачастую вычисляют редакционное расстояние, когда ищут мутации, вызывающие болезни.
Редакционное расстояние между двумя строками определяется как минимальное число односимвольных вставок, удалений и замен, необходимых для преобразования одной строки в другую.
- Входные данные: Две строки, состоящие из строчных букв латинского алфавита.
- Выходные данные: Редакционное расстояние между строками.
- Ограничения: Длина обеих строк не меньше и не больше .
Пример 1
|
Ввод |
Вывод |
|
short |
3 |
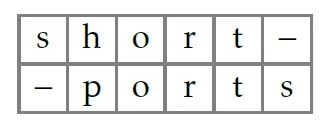
- Вторую строку можно получить из первой, удалив s, заменив h на p и вставив s. Это можно компактно продемонстрировать следующим выравниванием.
Пример 2
|
Ввод |
Вывод |
|
editing |
5 |
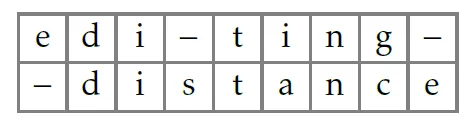
- Удалить e, вставить s после i, заменить i на a, заменить g на c, вставить e в конце.
Пример 3
|
Ввод |
Вывод |
|
ab |
0 |
- Совет: будьте осторожны с рекурсией.
Решение
Рассмотрим решение задачи. Выравнивание двух строк в двухрядной матрице осуществляется таким образом, чтобы первый (второй) ряд содержал упорядоченные символы первой (второй) строки, которые перемежаются пробелами («»).
В колонке не может быть два пробела одновременно в обеих строках.
Упражнение
Вычислите количество разных пар выравненных строк длиной и .
Мы классифицируем колонки выравнивания следующим образом (первый символ из верхней строки, второй — из нижней):
— колонка с символом и пробелом
— это удаление;
— колонка с пробелом и символом
— вставка;
— колонка с двумя одинаковыми символами
— совпадение;
— колонка с двумя разными символами
— это несоответствие.
Мы ищем выравнивание, при котором минимизируется общее количество несоответствий, удалений и вставок.
Выравнивание считается оптимальным по сравнению со всеми другими возможными вариантами, если оно содержит минимум несоответствий, удалений и вставок.
Стоит обратить внимание, что может быть несколько различных оптимальных выравниваний.
Упражнение
Докажите, что задача на редакционное расстояние может быть сведена к поиску оптимального выравнивания двух строк.
В примере выше последняя колонка — это вставка. Отбросив эту колонку, мы получаем оптимальное выравнивание первой строки и префикса второй.
Рассмотрим идею рассчитать редакционное расстояние между каждой парой префиксов двух строк. Это более общая постановка задачи, но важно отметить, что, решив её, мы найдём ответ и на интересующий нас вопрос.
Решение
Имея строки и , мы рассмотрим их префиксы и длиной и и обозначим их редакционное расстояние .
Так как последняя колонка оптимального выравнивания и — это или вставка, или удаление, или несоответствие, или совпадение, имеем,
Базовый случай для этого рекуррентного соотношения — и :
Это можно выразить более кратко: если или , тогда
Псевдокод ниже делает из этого рекуррентного соотношения рекурсивный алгоритм и использует мемоизацию для избежания перевычислений.
1table = associative array
2
3EditDistance(A,B,i,j):
4 if table[i,j] is not yet computed:
5 if i=0 or j=0:
6 table[i,j] = max(i,j)
7 else:
8 insertion = EditDistance(A,B,i,j−1)+1
9 deletion = EditDistance(A,B,i−1,j)+1
10 match = EditDistance(A,B,i−1,j−1)
11 mismatch = EditDistance(A,B,i−1,j−1)+1
12 if A[i]=B[j]:
13 table[i,j] = min(insertion,deletion,match)
14 else:
15 table[i,j] = min(insertion,deletion,mismatch)
16 return table[i,j]
Время выполнения этого алгоритма составляет , так как выполняется не больше рекурсивных вызовов, которые добавляют значения в table.
Рекурсивный алгоритм
Рекурсивный алгоритм вычисляет для всех и . Из рекурсивного алгоритма можно сделать итерационный, который будет сохранять решения всех подзадач в двумерной таблице. Таблица заполняется по рядам проходами. Это гарантирует, что когда мы вычислим значение клетки , значения клеток , и будут уже готовы.
1EditDistance(A[1…n],B[1…m]):
2 table = 2d array of size (n+1) * (m+1)
3 table[0][j] = j for all i,j
4 for i from 1 to n:
5 for j from 1 to m:
6 insertion = table[i][j−1]+1
7 deletion = table[i−1][j]+1
8 match = table[i−1][j−1]
9 mismatch = table[i−1][j−1]+1
10 if A[i]=B[j]:
11 table[i][j] = min(insertion,deletion,match)
12 else:
13 table[i][j] = min(insertion,deletion,mismatch)
14 return table[n][m]
Итоговая таблица для нашего примера изображена на рисунке ниже. Значение каждой клетки вычисляется, исходя из значений соседних клеток сверху, слева и слева-сверху. У каждой клетки входящие стрелки указывают на один или несколько случаев (вставка, удаление, несоответствие, или совпадение), которые приводят к значению этой клетки.

Таблица соответствует ориентированному ациклическому графу, в котором все рёбра, за исключением синих, имеют длину . А синие ребра соответствуют совпадающим символам и имеют длину . Алгоритм находит на графе самый короткий путь от узла слева сверху до узла справа снизу.
Время выполнения алгоритма составляет . Ему требуется ячеек памяти для хранения двумерного массива table. Расход места может быть снижен до (и даже до ), если мы обратим внимание на то, что при заполнении текущего ряда таблицы нам нужны только клетки из текущего и предыдущего. Таким образом, вместо хранения всей таблицы достаточно сохранить текущий и предыдущие ряды.
Остановитесь и подумайте:
Вы рассчитали редакционное расстояние между editing и distance. Но как найти пять операций для того, чтобы преобразовать editing в distance?
Отметим, что любой путь от до на рисунке образовывает оптимальное выравнивание строк и .
Упражнение
Путь, изображённый на рисунке ниже, соответствует оптимальному выравниванию editing и distance. Сколько в этом выравнивании вставок, удалений, совпадений и несоответствий? Постройте оптимальное выравнивание, соответствующее этому пути.

Оптимальное выравнивание можно обнаружить с помощью перехода по стрелкам в обратную сторону от нижнего правого угла вдоль любого пути, приводящего к верхнему левому углу.
Что дальше
Теперь вы умеете вычислять редакционное расстояние — минимальное число правок, необходимых для преобразования одной строки в другую. Вы поняли, как формулируется задача рекурсивно, как работает динамическое программирование с таблицей и даже как найти оптимальное выравнивание.
Далее — задача на поиск наибольшей общей подпоследовательности (LCS). Вы увидите, как похожие идеи помогают решать другую важную задачу сравнения строк, и научитесь отличать LCS от редакционного расстояния.
А пока вы не ушли дальше — закрепите материал на практике:
- Отметьте, что урок прочитан, при помощи кнопки ниже.
- Пройдите мини-квиз, чтобы проверить, насколько хорошо вы усвоили тему.
- Перейдите к задачам этого параграфа и потренируйтесь.
- Перед этим — загляните в короткий гайд о том, как работает система проверки.
Хотите обсудить, задать вопрос или не понимаете, почему код не работает? Мы всё предусмотрели — вступайте в сообщество Хендбука! Там студенты помогают друг другу разобраться.
Ключевые выводы параграфа
- Редакционное расстояние — это минимальное число вставок, удалений и замен для превращения одной строки в другую.
- Его можно вычислить с помощью динамического программирования, заполняя таблицу расстояний между префиксами.
- Переходы в таблице соответствуют операциям редактирования и дают кратчайший путь в сетке выравнивания.
- Можно восстановить оптимальное выравнивание, двигаясь по таблице в обратную сторону.
- Решение можно оптимизировать по памяти, если хранить только два ряда таблицы одновременно.



