В этом параграфе вы познакомитесь с алгоритмом Дейкстры — одним из самых известных алгоритмов на графах. Он позволяет находить кратчайшие пути от одной вершины до всех остальных в графе без отрицательных весов. Вы узнаете, как работает идея постепенного уточнения расстояний, научитесь реализовывать алгоритм шаг за шагом и поймёте, как восстанавливается путь.
Ключевые вопросы параграфа
- Как устроен алгоритм Дейкстры и зачем нужны веса рёбер?
- Почему алгоритм не работает с отрицательными весами?
- Как восстановить кратчайший путь после завершения алгоритма?
Принцип работы алгоритма Дейкстры
Зачастую в графах требуется находить между вершинами кратчайшие пути. Один из алгоритмов нахождения кратчайших путей от заданной вершины до любой другой — алгоритм Дейкстры. Алгоритм работает только для графов без рёбер отрицательного веса.
Асимптотическая сложность нахождения компонент связности в графе — O(V+E), где V — число вершин, а E — число рёбер и дуг.
Опишем принцип работы алгоритма Дейкстры:
- Шаг 1. Всем вершинам, за исключением первой, присваивается вес равный бесконечности, а первой вершине — 0.
- Шаг 2. Все вершины не посещены.
- Шаг 3. Первая вершина объявляется текущей.
- Шаг 4. Вес всех невыделенных вершин пересчитывается по формуле: вес невыделенной вершины есть минимальное число из старого веса данной вершины, суммы веса текущей вершины и веса ребра, соединяющего текущую вершину с невыделенной.
- Шаг 5. Среди невыделенных вершин ищется вершина с минимальным весом. Если такова не найдена, то есть вес всех вершин равен бесконечности, то маршрута не существует. Следовательно, выход. Иначе, текущей становится найденная вершина. Она же выделяется.
- Шаг 6. Если текущей вершиной оказывается конечная, то путь найден, и его вес есть вес конечной вершины.
- Шаг 7. Переход на шаг 4.
Пример работы алгоритма показан на картинке ниже.
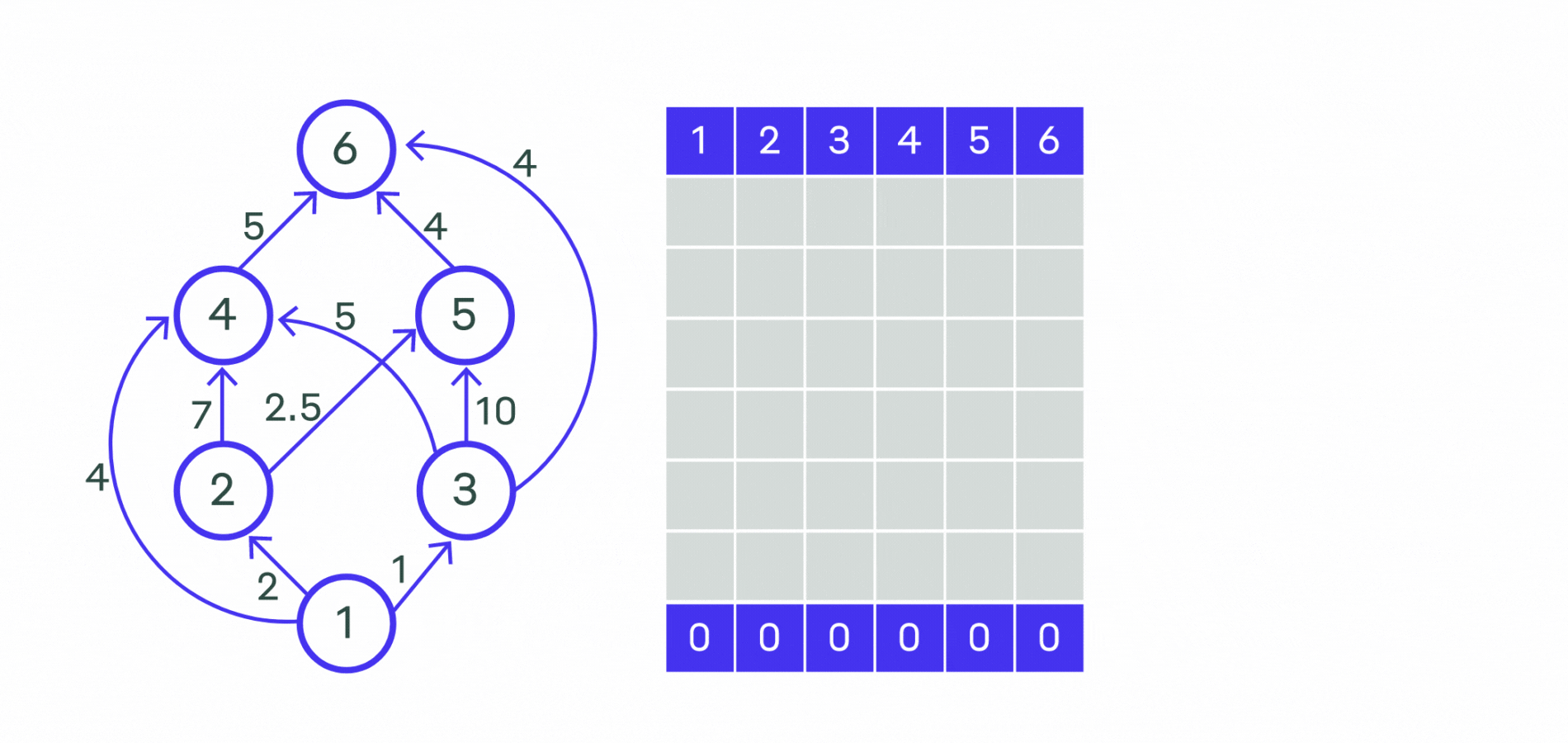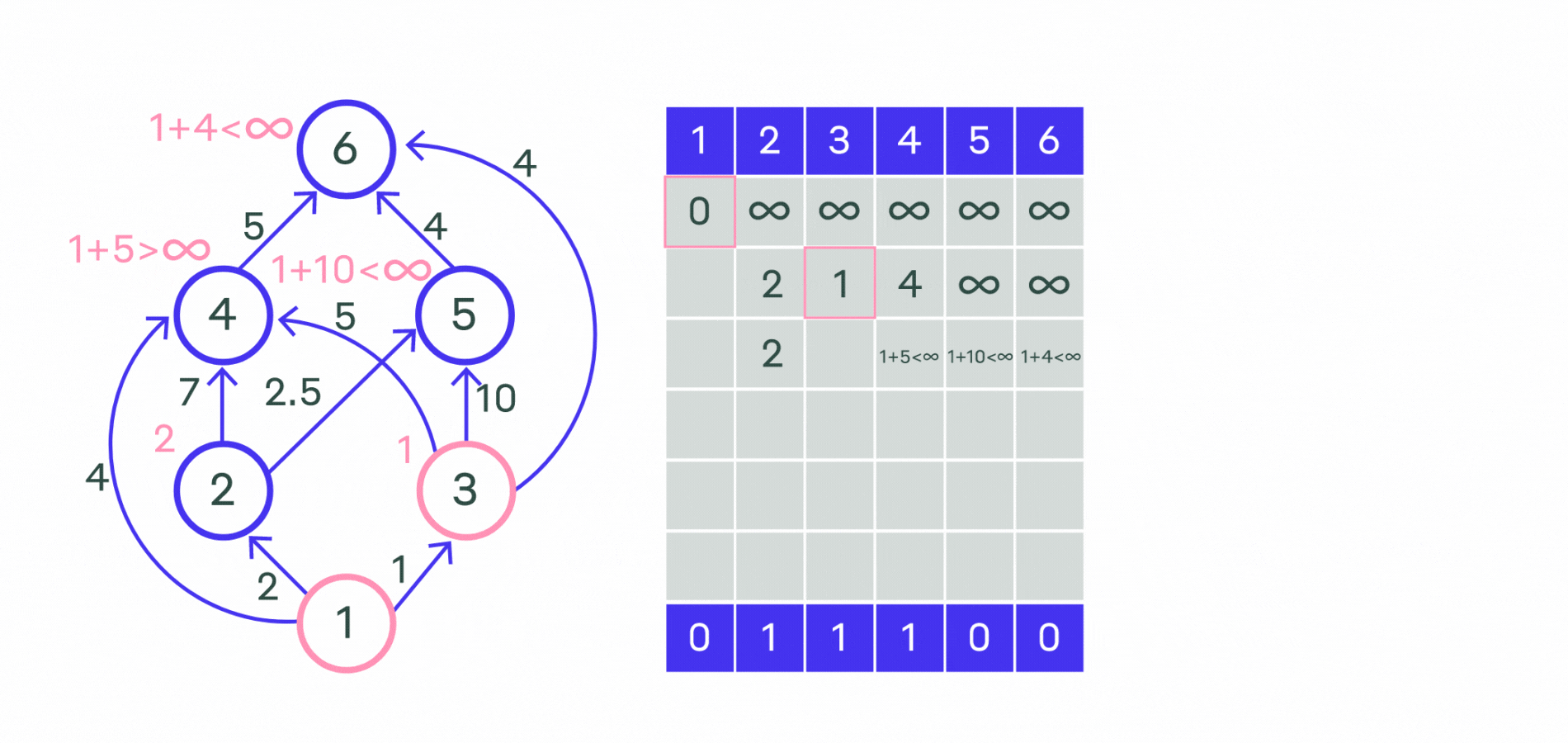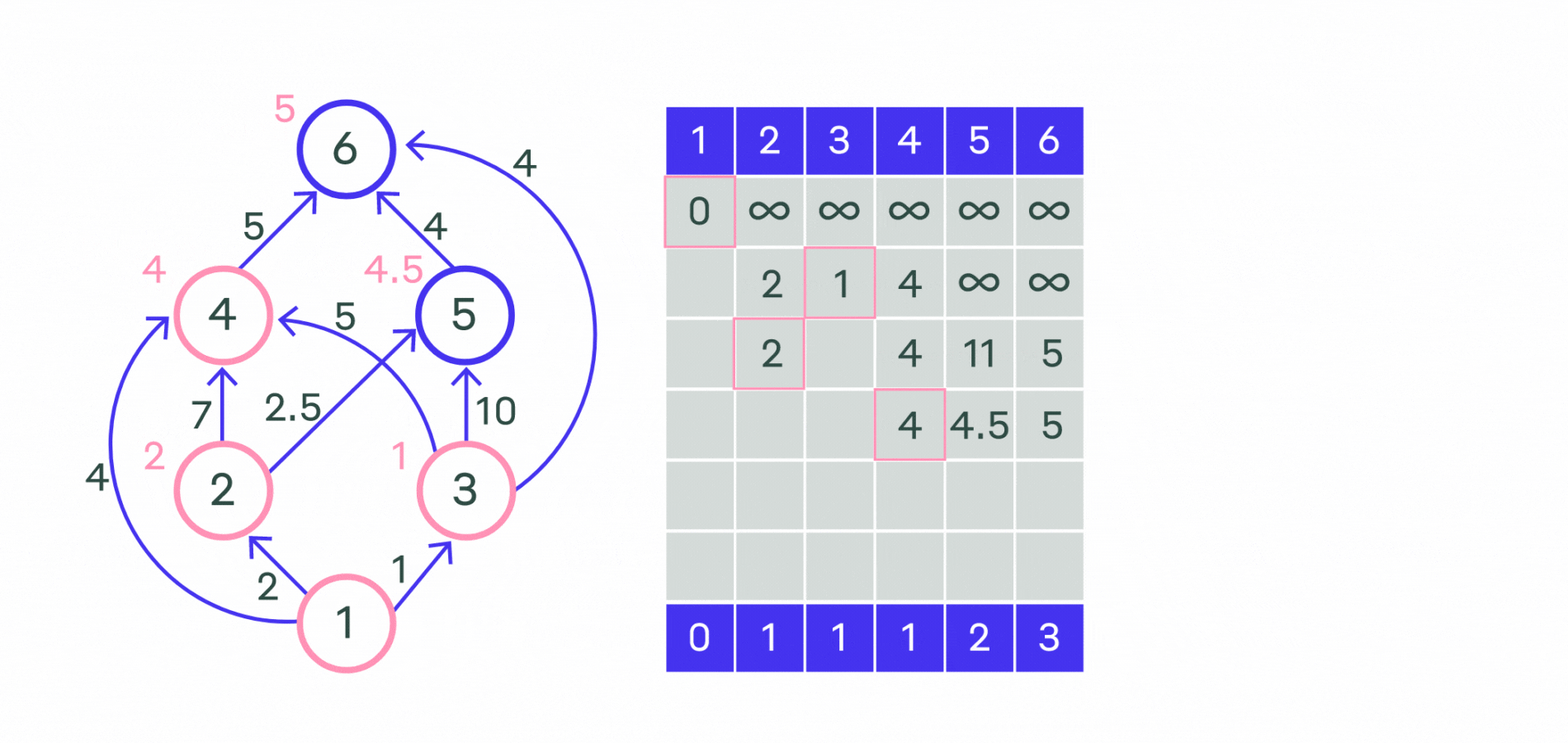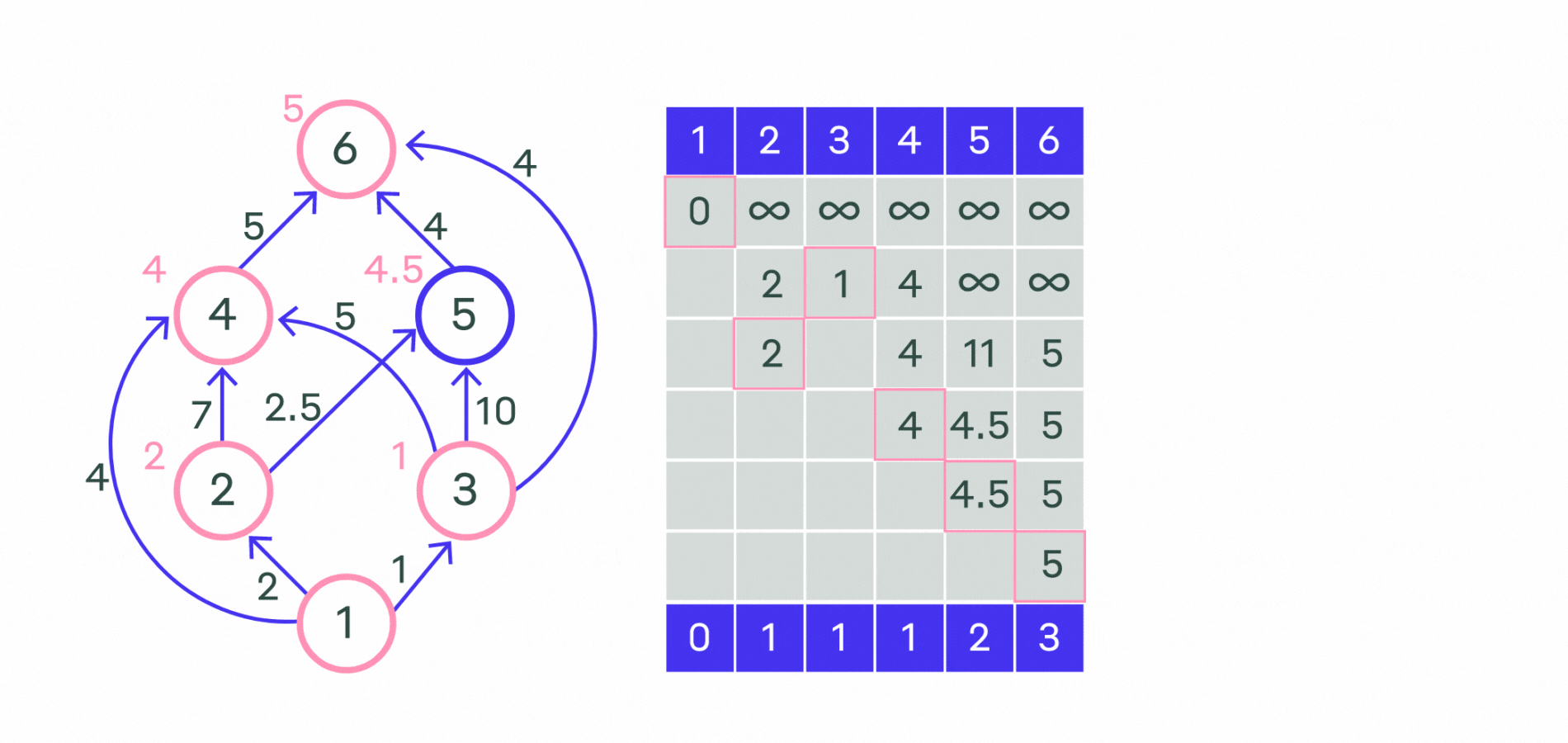
Посмотрим на реализацию.
1Dijkstra(graph, start, finish, used):
2 vector d(n, inf), p(n, -1)
3 n = len(graph)
4 graph[v] = 1
5 for (int i = 0; i < n; ++i)
6 int v = -1
7 for (int j = 0; j < n; ++j)
8 if (!used[j] and (v == -1 or d[j] < d[v]))
9 v = j
10 used[v] = true
11 for (int j = 0; j < len(graph[v]); ++j)
12 to = graph[v][i].vertex
13 len = graph[v][i].edge
14 if (d[v] + len < d[to])
15 d[to] = d[v] + len
16 p[to] = v
Асимптотическая сложность алгоритма Дейкстры — , где — число вершин, а — число рёбер и дуг.
Упражнение 1
Подумайте, как восстановить путь, используя введённый массив p?
Упражнение 2
Как изменится кратчайший путь, если все веса рёбер увеличить на какое-то число?
Упражнение 3
Как изменится кратчайший путь, если все веса рёбер увеличить в какое-то число раз?
Упражнение 4
Подумайте, почему алгоритм работает только для графов без рёбер отрицательного веса?
Что дальше
Теперь вы умеете находить кратчайшие пути в графах с помощью алгоритма Дейкстры. Вы научились пошагово уточнять расстояния до вершин, работать с массивом предков и восстанавливать путь. Вы также поняли, в каких случаях алгоритм применим, а в каких — нет.
Далее — завершение главы. Мы кратко подведём итоги, сравним изученные подходы и обобщим стратегии, которые помогут вам уверенно решать задачи на графы.
А пока вы не ушли дальше — закрепите материал на практике:
- Отметьте, что урок прочитан, при помощи кнопки ниже.
- Пройдите мини-квиз, чтобы проверить, насколько хорошо вы усвоили тему.
- Перейдите к задачам этого параграфа и потренируйтесь.
- Перед этим — загляните в короткий гайд о том, как работает система проверки.
Хотите обсудить, задать вопрос или не понимаете, почему код не работает? Мы всё предусмотрели — вступайте в сообщество Хендбука! Там студенты помогают друг другу разобраться.
Ключевые выводы параграфа
- Алгоритм Дейкстры находит кратчайшие пути от одной вершины до всех остальных в графе без отрицательных рёбер.
- Идея алгоритма — постепенно уточнять расстояния, переходя от ближайших вершин к более дальним.
- Для восстановления пути используется массив предков.
- Алгоритм не работает корректно при наличии отрицательных весов — для таких случаев нужны другие подходы (например, Беллмана — Форда).


