В этом параграфе вы познакомитесь с двумя базовыми способами обхода графа — обходом в глубину (Depth-First Search, DFS) и обходом в ширину (Breadth-First Search, BFS). Эти алгоритмы позволяют находить пути, проверять достижимость вершин и анализировать структуру графа. Кроме того, они часто становятся строительными блоками для более сложных методов работы с графами. Вы научитесь реализовывать оба способа, понимать, когда применять каждый из них, и избегать типичных ошибок при обходе.
Ключевые вопросы параграфа
- Как работает обход графа в глубину и в ширину и в чём между ними разница?
- Что важно учитывать при реализации DFS и BFS?
- Как не попасть в бесконечный цикл и правильно отслеживать посещённые вершины?
Алгоритмы на графах
Пришла пора рассмотреть первые алгоритмы на графах. К классическим алгоритмам относятся обходы графов. Под обходом графа обычно понимают процесс систематического просмотра всех вершин или рёбер графа, чтобы найти некоторые вершины, удовлетворяющие определённым условиям. Мы рассмотрим обход в ширину и обход в глубину.
Обход в глубину заключается в систематическом просмотре вершин графа и прохождении его ветвями. Иными словами, идея поиска в глубину — когда возможные пути по рёбрам, выходящим из вершин, разветвляются, нужно сначала полностью исследовать одну ветку и только потом переходить к другим веткам (если они останутся нерассмотренными).
Опишем алгоритм поиска в глубину:
- Шаг 1. Все вершины графа отмечаем, как не посещенные. Выбирается первая вершина и помечается как посещённая.
- Шаг 2. Для последней помеченной как посещённой вершины выбирается смежная вершина, которая первая помеченная как не посещенная, и ей присваивается значение посещённой. Если таких вершин нет, то берётся предыдущая помеченная вершина.
- Шаг 3. Повторяем шаг 2 до тех пор, пока все вершины не будут помечены как посещённые.
Пример реализации приведён ниже.
1DFS(graph, v, used):
2 used[v] = 1
3 for (var u : graph[v])
4 if (!used[u])
5 DFS(graph, u, used)
Упражнение
Попробуйте выполнить алгоритм поиска в глубину пошагово для графа.
Обратите внимание, сейчас мы посмотрели на рекурсивную реализацию. Конечно, преимущество использования рекурсивного подхода заключается в простоте его написания, однако, рекурсивный подход имеет свои ограничения.
Можно переписать алгоритм поиска в глубину с использованием особых структур данных. Например, стека.
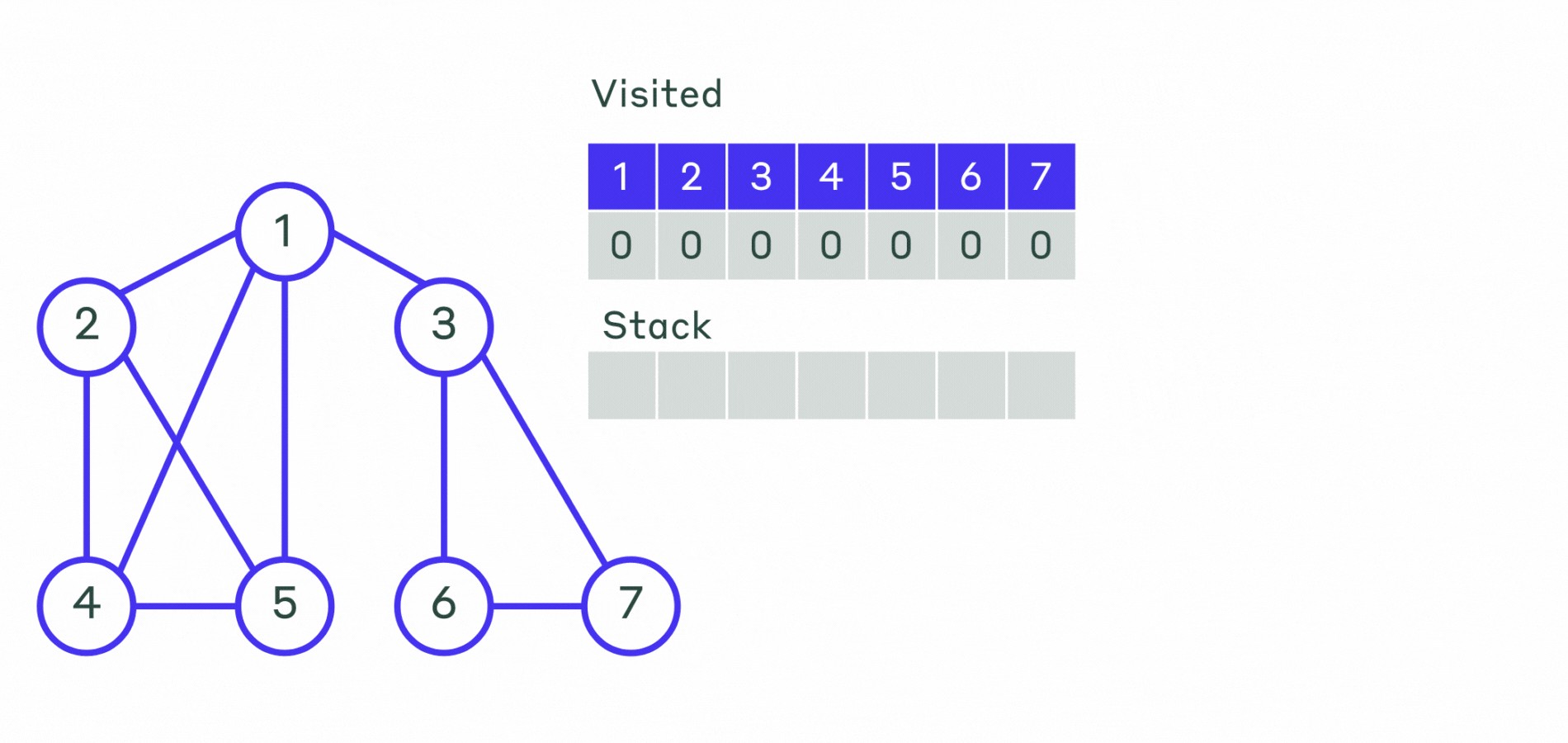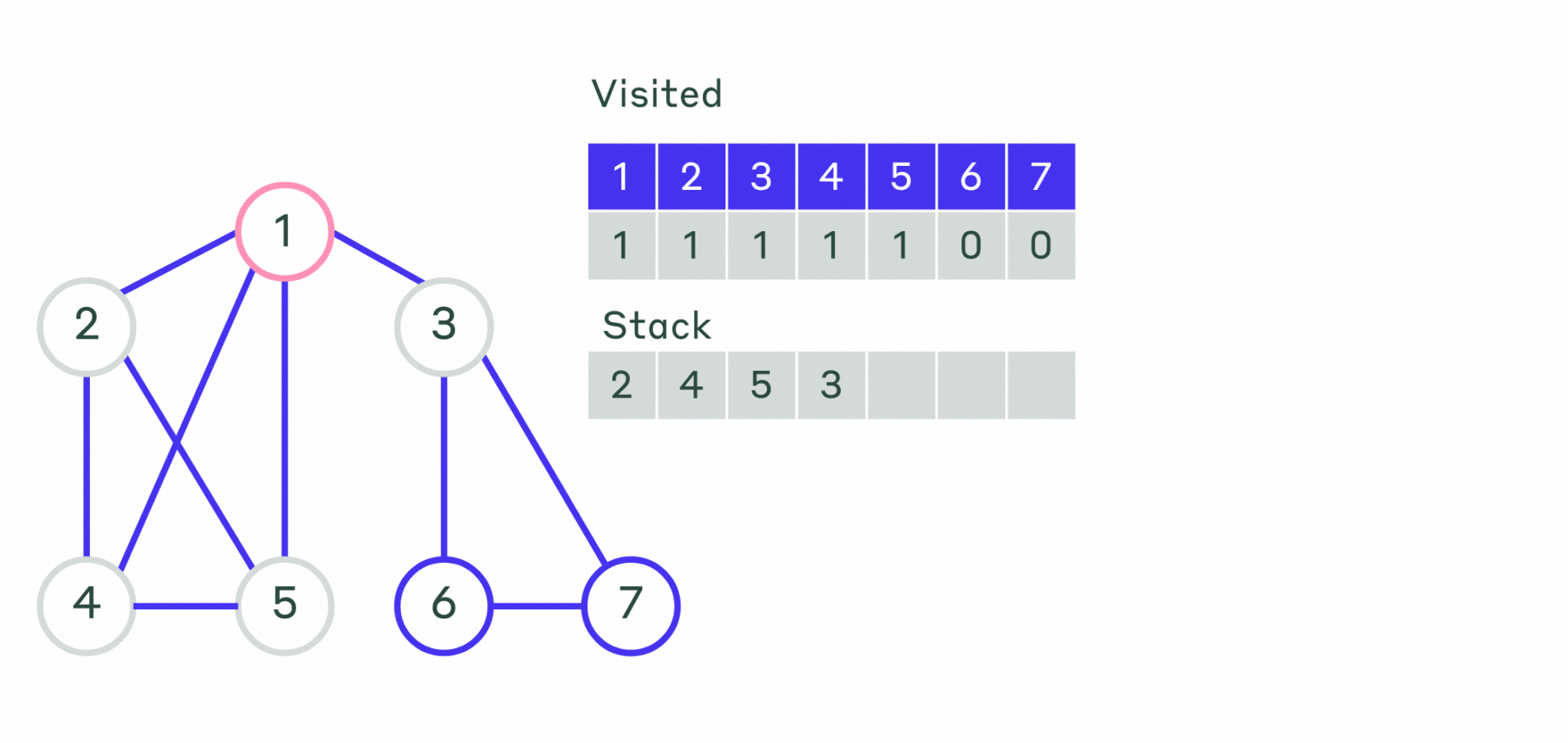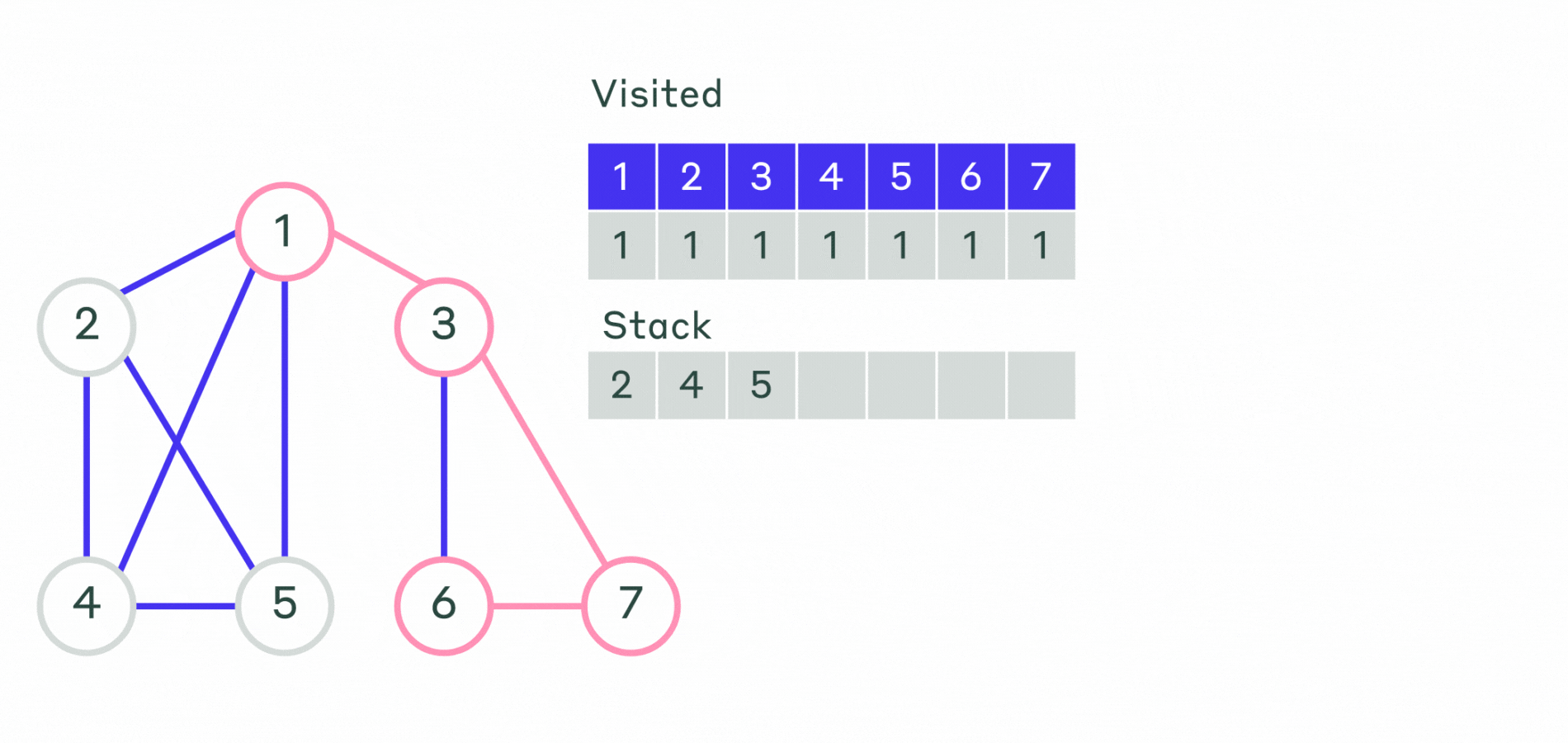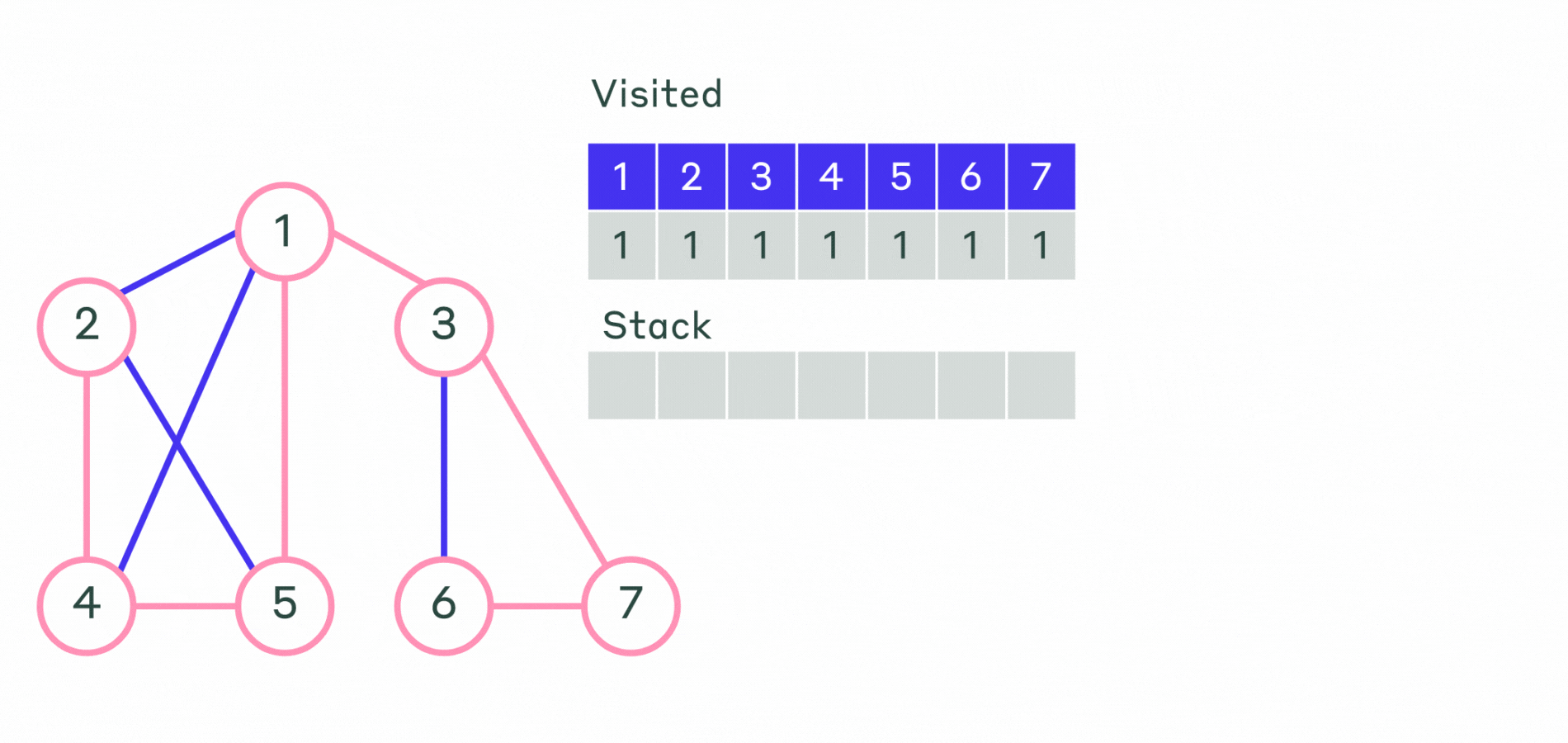
Опишем алгоритм поиска в глубину в нерекурсивной форме:
- Шаг 1. Все вершины графа отмечаем, как не посещённые. Выбирается первая вершина и помечается как посещённая. Эту вершину кладем в контейнер — стек.
- Шаг 2. Пока стек не пустой:
- Извлекаем последнюю добавленную вершину.
- Просматриваем все смежные с ней не посещённые вершины и помещаем их в стек.
Порядок выхода вершин из стека и будет порядком обхода вершин графа.
Пример работы не рекурсивного алгоритма можно посмотреть на анимации.
Пример реализации приведён ниже.
1DFS(graph, v, used):
2 stack q
3 q.push(v)
4 used[v] = 1
5 while(!q.empty())
6 v = q.front()
7 q.pop()
8 for (var to : graph[v]):
9 if (!used[to]):
10 used[to] = true
11 q.push(to)
Ещё один способ обхода графа — обход в ширину. Основное его отличие в том, что сначала исследуются смежные вершины, а уже потом вершины на следующем уровне. Иначе говоря, сначала исследуются все вершины, смежные с начальной вершиной (вершина с которой начинается обход). Эти вершины находятся на расстоянии 1 от начальной. Затем исследуются все вершины на расстоянии 2 от начальной, затем все на расстоянии 3 и так далее. Обратим внимание, что при этом для каждой вершины сразу находятся длина кратчайшего маршрута от начальной вершины.
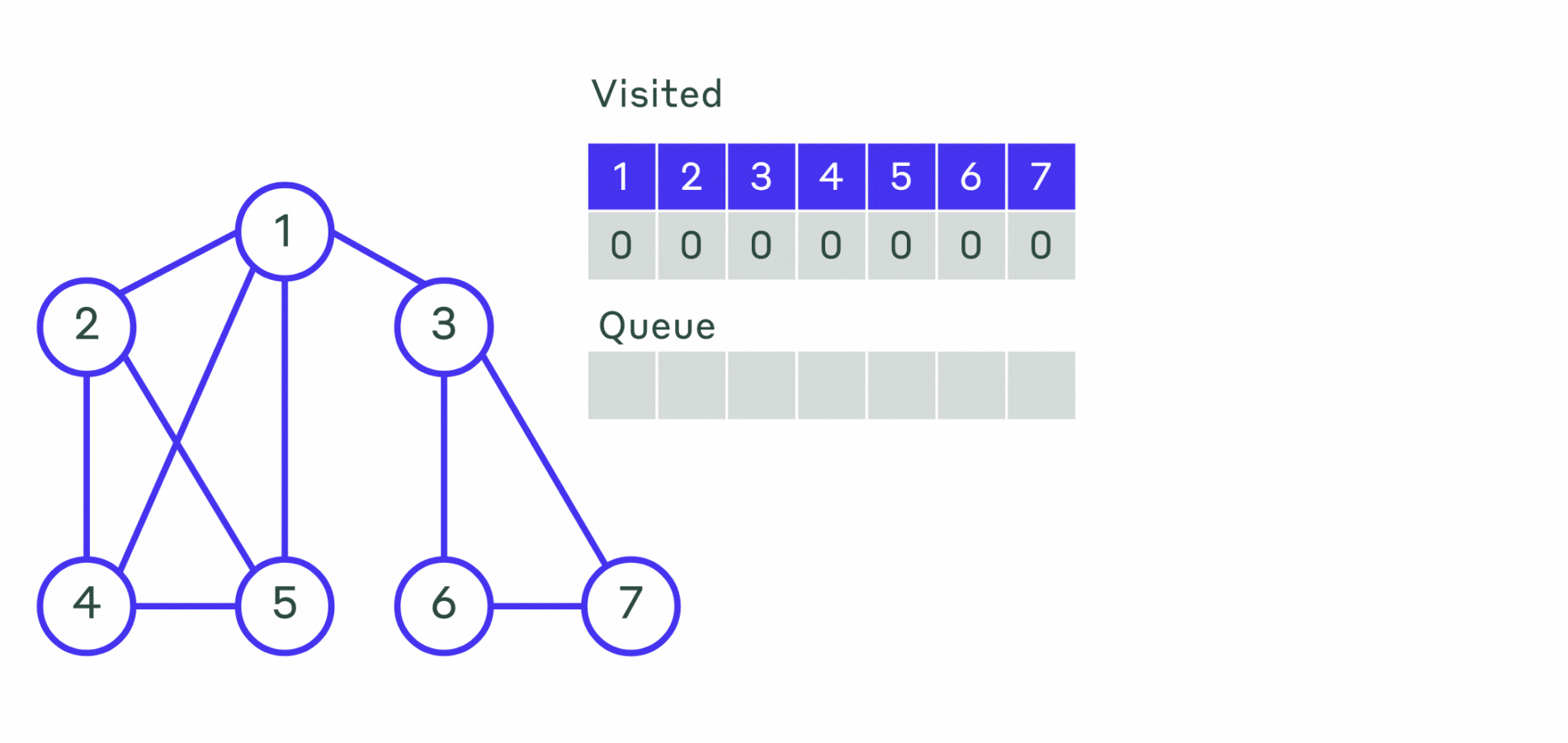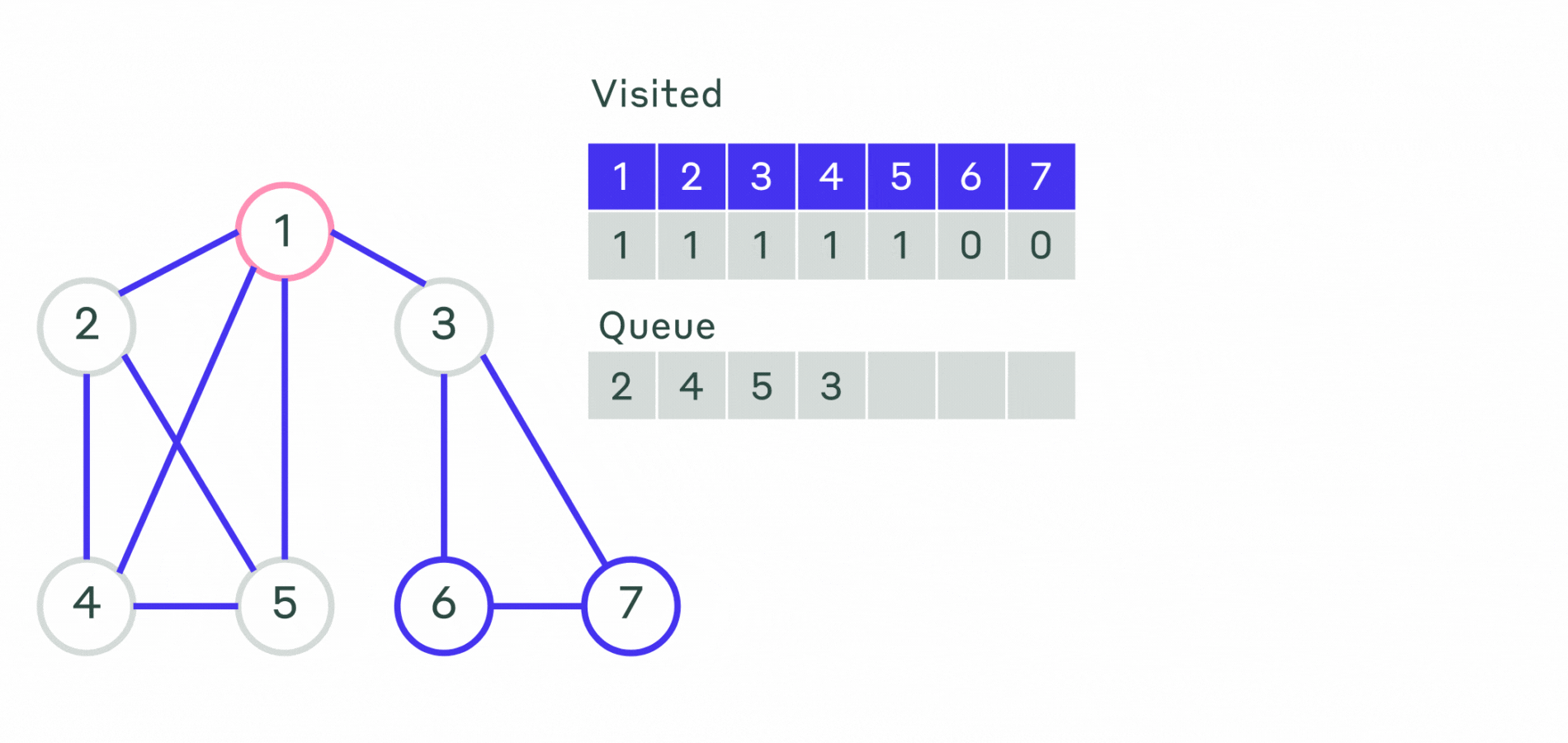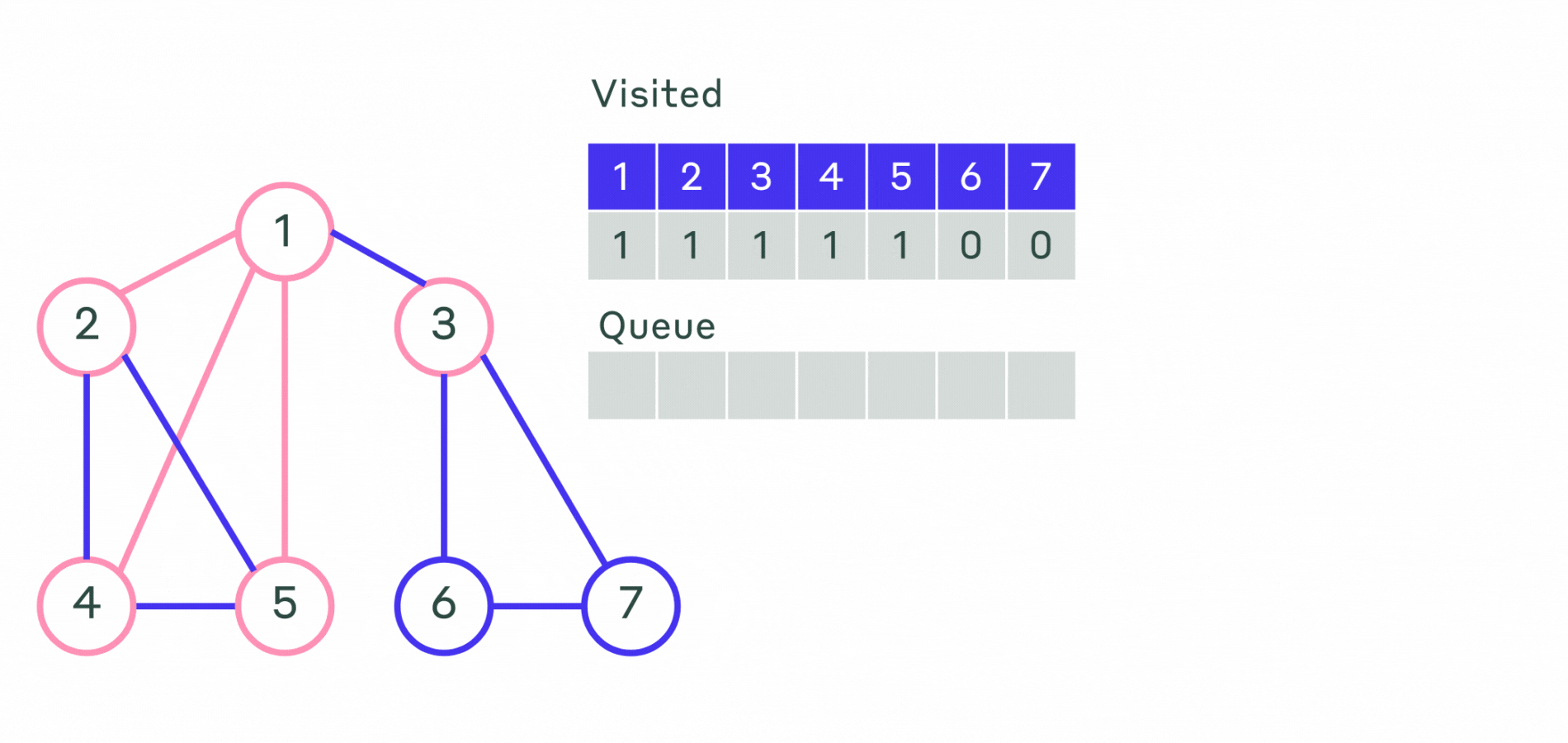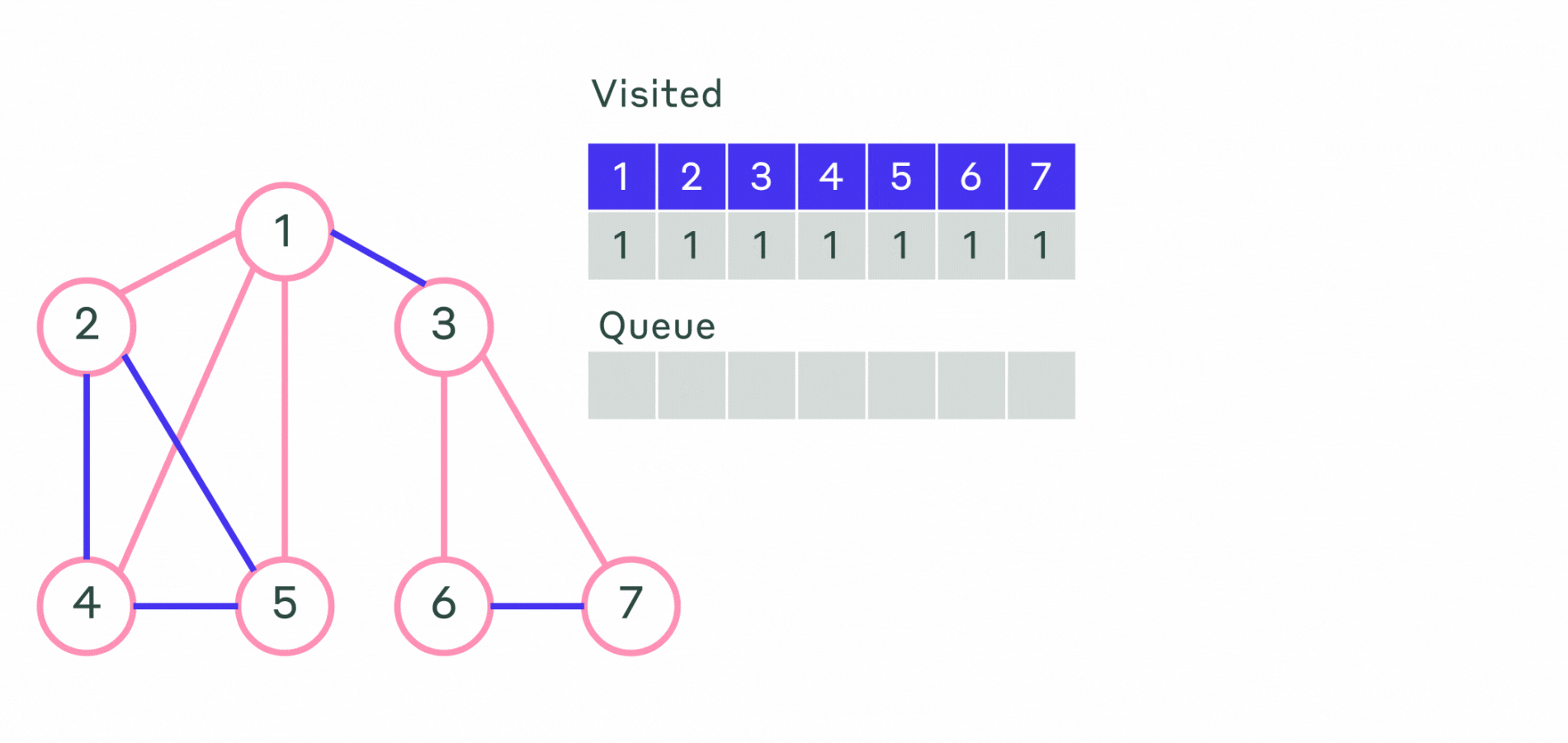
Опишем алгоритм поиска в ширину:
- Шаг 1. Всем вершинам графа присваивается значение не посещённой. Выбирается первая вершина и помечается как посещённая и заносится в очередь.
- Шаг 2. Посещается первая вершина из очереди (если она не помечена как посещённая). Все её соседние вершины заносятся в очередь. После этого она удаляется из очереди.
- Шаг 3. Повторяется шаг 2 до тех пор, пока очередь не станет пустой.
Пример реализации алгоритма можно посмотреть на анимации
Пример реализации приведён ниже.
1BFS(graph, v, used):
2 queue q
3 q.push(v)
4 used[v] = 1
5 while(!q.empty())
6 v = q.front()
7 q.pop()
8 for (var to : graph[v]):
9 if (!used[to]):
10 used[to] = true
11 q.push(to)
Упражнение
Подумайте, какое отличие алгоритма поиска в ширину от алгоритма поиска в глубину?
Асимптотическая сложность алгоритма поиска в глубину и ширину — , где — число вершин, а — число рёбер и дуг. Обходы графов могут применяться для решения задач, связанных с теорией графов:
- Волновой алгоритм поиска пути в лабиринте.
- Волновая трассировка печатных плат.
- Поиск компонент связности в графе.
- Поиск кратчайшего пути между двумя узлами невзвешенного графа.
- Поиск в пространстве состояний: нахождение решения задачи с наименьшим числом ходов, если каждое состояние системы можно представить вершиной графа, а переходы из одного состояния в другое — рёбрами графа.
- Нахождение кратчайшего цикла в ориентированном невзвешенном графе.
- Нахождение всех вершин и рёбер, лежащих на каком-либо кратчайшем пути между двумя вершинами.
- Поиск увеличивающего пути в алгоритме Форда-Фалкерсона (алгоритм Эдмондса-Карпа).
Что дальше
Теперь вы умеете реализовывать обходы графа — DFS и BFS — и использовать их для решения базовых задач, таких как проверка достижимости и построение пути. Вы научились работать с очередью и стеком, отмечать посещённые вершины и корректно обходить даже сложные структуры.
Далее — задача на использование обходов. Вы узнаете, как при помощи DFS или BFS найти компоненты связности и почему важно запускать обход из каждой новой вершины.
А пока вы не ушли дальше — закрепите материал на практике:
- Отметьте, что урок прочитан, при помощи кнопки ниже.
- Пройдите мини-квиз, чтобы проверить, насколько хорошо вы усвоили тему.
- Перейдите к задачам этого параграфа и потренируйтесь.
- Перед этим — загляните в короткий гайд о том, как работает система проверки.
Хотите обсудить, задать вопрос или не понимаете, почему код не работает? Мы всё предусмотрели — вступайте в сообщество Хендбука! Там студенты помогают друг другу разобраться.
Ключевые выводы параграфа
- DFS и BFS — базовые алгоритмы, применимые ко многим задачам на графах.
- DFS использует стек (в том числе неявный при рекурсии), а BFS — очередь.
- Для корректного обхода важно отслеживать посещённые вершины.
- Выбор между DFS и BFS зависит от задачи: от поиска пути до анализа структуры графа.


