В этом параграфе вы познакомитесь с одним из самых мощных и простых приёмов в программировании — рекурсией. Мы разберём, как функция может вызывать саму себя и как при этом решаются задачи. На примере головоломки «Ханойские башни» вы увидите, как с помощью рекурсии можно элегантно описать сложный процесс и почему такие решения могут работать долго.
Ключевые вопросы параграфа
- В чём сила и в чём слабость рекурсии по сравнению с итеративным подходом?
- Как разложение задачи на подзадачи помогает описывать решения?
- Что показывает пример «Ханойских башен» о возможностях и ограничениях рекурсивных алгоритмов?
Что такое рекурсия
Рекурсия — одно из самых распространенных алгоритмических понятий. Если говорить просто, то рекурсивным алгоритм становится, если вызывает сам себя.
Головоломка «Ханойские башни»
Головоломка «Ханойские башни» состоит из трёх стержней, пронумеруем их слева направо: 1, 2 и 3. Также в головоломке используется стопка дисков с отверстием посередине. Радиус дисков уменьшается снизу вверх.
- Изначально диски расположены на левом стержне (стержень 1), самый большой диск находится внизу.
- Диски в игре перемещаются по одному со стержня на стержень.
- Диск можно надеть на стержень, только если он пустой или верхний диск на нём большего размера, чем перемещаемый.
Цель головоломки — перенести все диски со стержня 1 на стержень 3. Попробуйте нашу интерактивную версию «Ханойских башен» и узнайте, как переместить все диски с одного стержня на другой.
Вывод списка действий, необходимых для решения головоломки «Ханойские башни».
- Входные данные: Целое число .
- Выходные данные: Последовательность ходов для решения головоломки «Ханойские башни» из дисков.
Решение головоломки
Решить головоломку с одним диском легко — просто переместите его на правый стержень. Головоломка на два диска ненамного сложнее. Сначала нужно переместить маленький диск на стержень посередине, а большой — на стержень справа. Затем переместить маленький диск на большой на правом стержне.
Версия на три диска чуть сложнее, но и ее можно решить с помощью следующих семи шагов:
- Переместить диск со стержня 1 на стержень 3
- Переместить диск со стержня 1 на стержень 2
- Переместить диск со стержня 3 на стержень 2
- Переместить диск со стержня 1 на стержень 3
- Переместить диск со стержня 2 на стержень 1
- Переместить диск со стержня 2 на стержень 3
- Переместить диск со стержня 1 на стержень 3
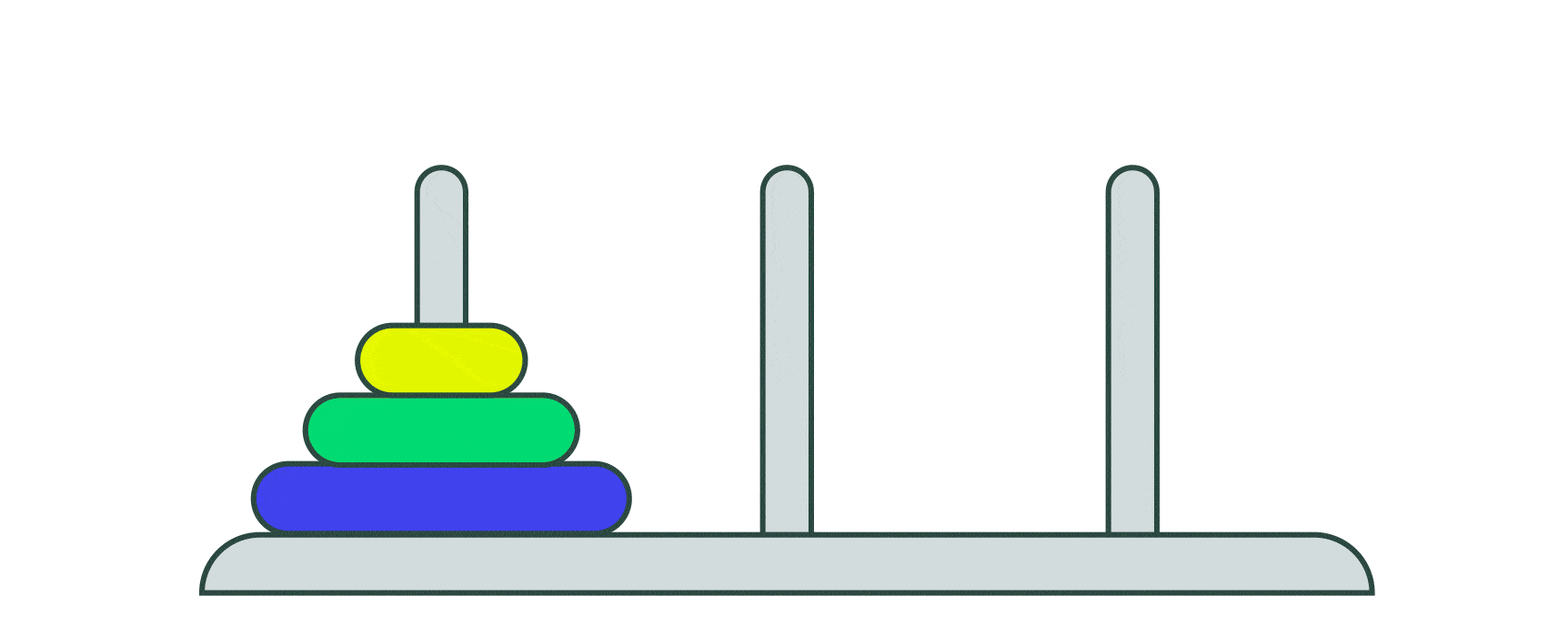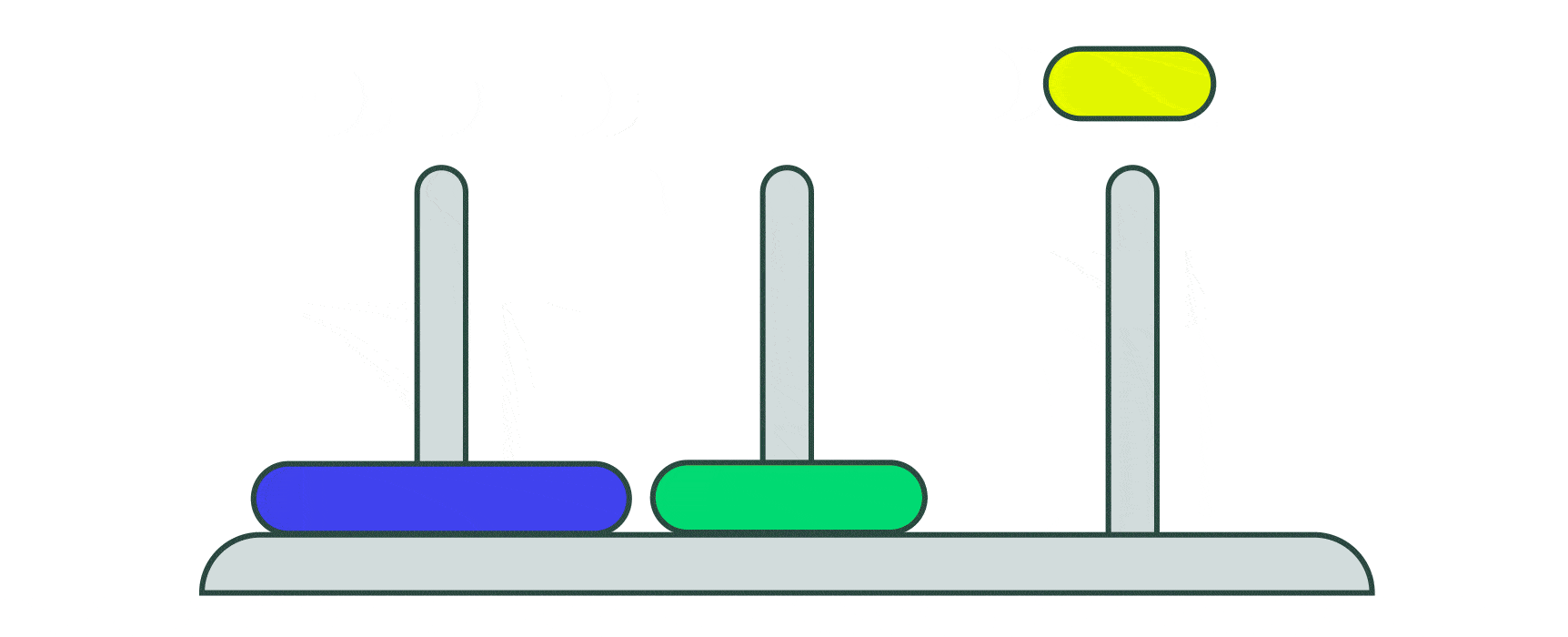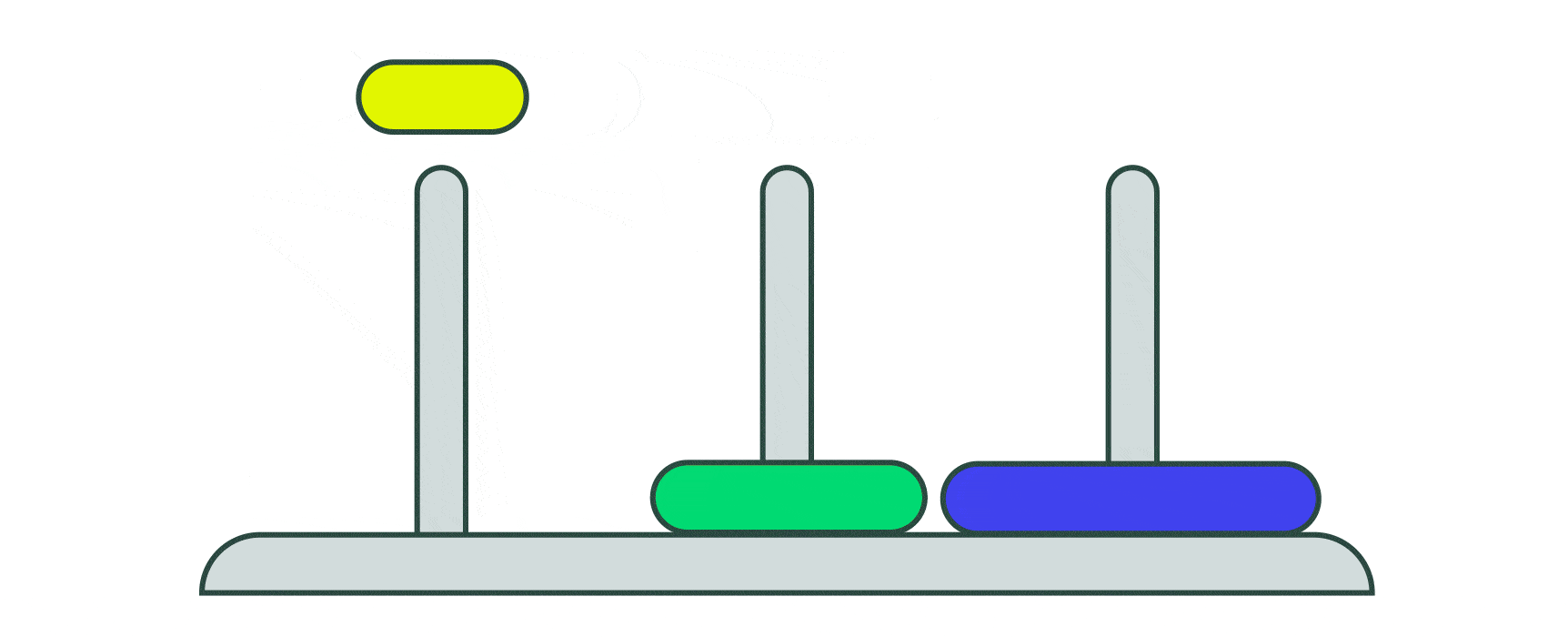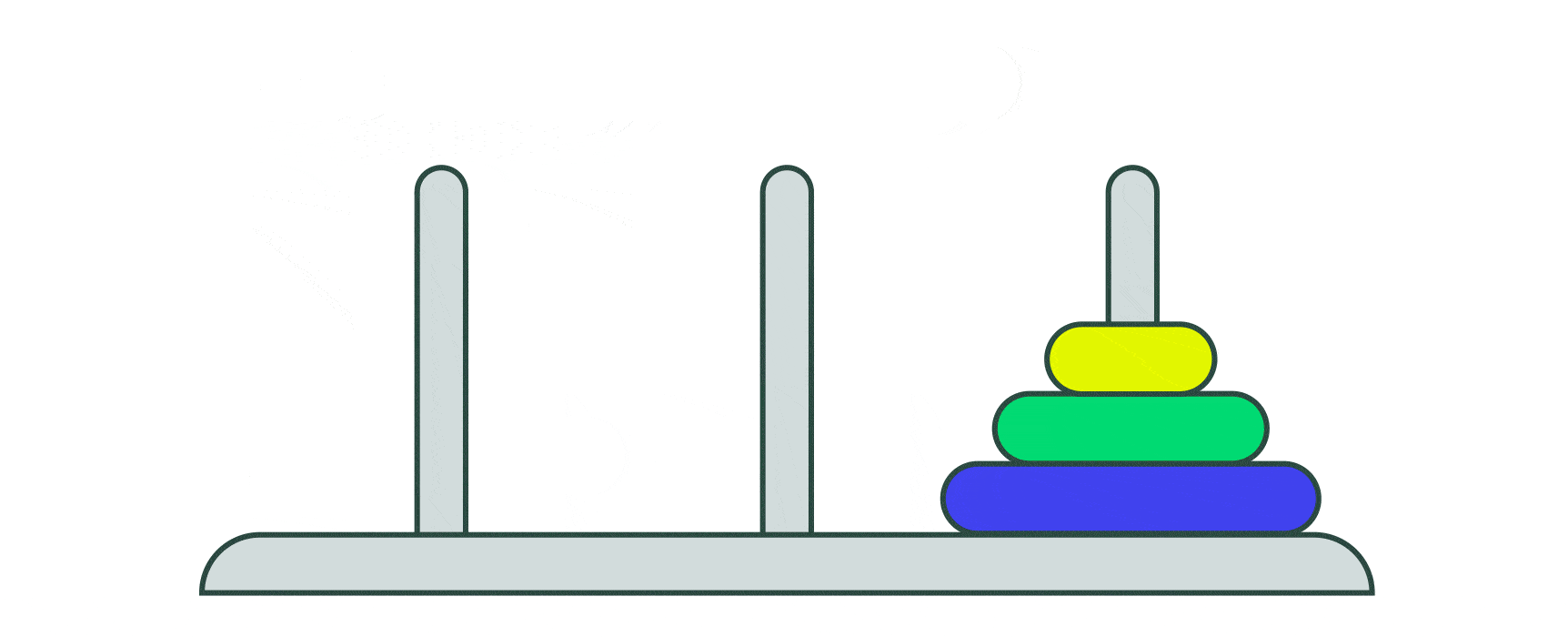
Подсчёт количества шагов для решения версии на четыре диска
Теперь давайте посчитаем, сколько шагов потребуется для решения версии на четыре диска.
- Нам нужно обязательно переместить самый большой диск, но для этого придётся сперва поместить все остальные диски на пустой стержень.
- Если у нас не три диска, а четыре, то нужно переложить три верхних диска на пустой стержень (7 действий), а затем переместить самый большой диск (1 действие).
- Теперь нужно снова переместить три диска с «временного» стержня на самый большой диск (еще 7 действий). Весь процесс будет состоять из действий.
Обобщим
- Чтобы переместить дисков с левого стержня на правый, сначала необходимо переместить дисков на стержень посередине.
- Затем, когда диск под номером , самый большой, оказывается на правом стержне, нужно переместить на него оставшиеся диски со стержня посередине.
- Чтобы переместить дисков со стержня посередине направо, нужно сначала переместить дисков на стержень слева, затем переместить -й диск вправо, потом переместить дисков с левого стержня на правый и так далее.
Рекурсивный алгоритм в решении головоломки
На первый взгляд задача «Ханойские башни» может показаться сложной. Тем не менее данный рекурсивный алгоритм находит нужные перемещения дисков всего за 8 строк!
1 HanoiTowers(n,fromPeg,toPeg)
2 if n = 1:
3 output “Move disk from peg fromPeg to peg toPeg”
4 return
5 unusedPeg = 6 - fromPeg - toPeg
6 HanoiTowers(n−1,fromPeg,unusedPeg)
7 output “Move disk from peg fromPeg to peg toPeg”
8 HanoiTowers(n−1,unusedPeg,toPeg)
Переменные и указывают на три разных стержня.
Таким образом, HanoiTowers(n, 1, 3) перемещает диски ( шт.) с первого стержня на третий. Переменная указывает, какой из трёх стержней можно использовать для временного хранения первых () дисков.
Обратите внимание, что всегда равняется . Таким образом, значение переменной можно определить как .
Представленная таблица показывает результаты для всех возможных переменных и .
|
fromPeg |
toPeg |
unusedPeg |
|
1 |
2 |
3 |
|
1 |
3 |
2 |
|
2 |
1 |
3 |
|
2 |
3 |
1 |
|
3 |
1 |
2 |
|
3 |
2 |
1 |
Определив как , операторы выполняют более простую задачу: они сначала перемещают дисков на временный стержень, затем перекладывают большой диск, а потом складывают на него оставшиеся дисков.
1HanoiTowers(n−1,fromPeg,unusedPeg)
2output “Move disk from peg fromPeg to peg toPeg”
3HanoiTowers(n−1,unusedPeg,toPeg)
Обратите внимание, что нет необходимости указывать, какой диск игрок должен переложить с на : перемещается всегда тот диск, что является верхним на .
Остановитесь и подумайте:
Сколько нужно действий, чтобы переместить дисков?
Рекурсивное дерево в головоломке
Хотя решение Ханойских башен можно уложить в 9 строк псевдокода, его выполнение займет на удивление много времени. Решение головоломки на пять дисков состоит из 31 действия. А в решении башни из сотни дисков количество действий будет исчисляться “страшными” нонилионами.
Такое резкое увеличение числа действий для HanoiTowers неудивительно. Заметим, что каждый раз, когда вызывается HanoiTowers(n, 1, 3), алгоритм дважды вызывает сам себя для перемещения дисков, что запускает четыре вызова для перемещения дисков и так далее.
Это можно проиллюстрировать с помощью рекурсивного дерева, изображенного на рис.. Вызов HanoiTowers(4, 1, 3) приводит к вызовам HanoiTowers(3, 1, 2) и HanoiTowers(3, 2, 3); каждый из них вызывает HanoiTowers(2, 1, 3), HanoiTowers(2, 3, 2) и HanoiTowers(2, 2, 1), HanoiTowers(2, 1, 3) и так далее. Каждый вызов подпрограммы HanoiTowers занимает определенное время. Мы хотим узнать, сколько времени уйдёт на такой алгоритм.

Вычисление времени на алгоритм в головоломке
Чтобы вычислить время выполнения HanoiTowers размера , мы введём в рассмотрение функцию — количество перемещений дисков, которые выполняет HanoiTowers(n). Получается следующее уравнение:
Начиная с , это рекуррентное соотношение задаёт последовательность:
и так далее. Мы можем вычислить , прибавив 1 с обеих сторон и обнаружив, что
Если мы введём новое обозначение, , то . Таким образом, нужно решить следующее рекуррентное соотношение:
Начиная с , получаем последовательность
То есть, и . Следовательно, HanoiTowers(n) — экспоненциальный алгоритм.
Что дальше
Теперь вы знаете, как работает рекурсия и почему она может быть мощным инструментом для построения алгоритма. Вы научились разбивать задачу на шаги, каждый из которых решается тем же способом, что и вся задача целиком.
Далее — алгоритмы «Разделяй и властвуй». Мы разберём, как делить задачу на независимые части, решать каждую по отдельности и собирать общее решение. Вы увидите, как этот подход ложится в основу быстрой сортировки и других эффективных алгоритмов.
А пока вы не ушли дальше — закрепите материал на практике:
- Отметьте, что урок прочитан, при помощи кнопки ниже.
- Пройдите мини-квиз, чтобы проверить, насколько хорошо вы усвоили тему.
- Перейдите к задачам этого параграфа и потренируйтесь.
- Перед этим — загляните в короткий гайд о том, как работает система проверки.
Хотите обсудить, задать вопрос или не понимаете, почему код не работает? Мы всё предусмотрели — вступайте в сообщество Хендбука! Там студенты помогают друг другу разобраться.
Ключевые выводы параграфа
- Рекурсия — это подход, при котором функция вызывает саму себя для решения подзадачи.
- Чтобы рекурсивное решение работало, важно определить базовый случай и убедиться, что каждый шаг приближает нас к нему.
- Задача «Ханойские башни» — классический пример, в котором рекурсивная стратегия описывает процесс из десятков или сотен шагов с минимальным кодом.
- Количество операций в рекурсивных алгоритмах может расти экспоненциально — это важно учитывать при выборе метода решения задачи.



