Как с помощью моделей мы можем прогнозировать результаты и почему поведение этих моделей может резко меняться при малых изменениях в данных?
Ответы на эти вопросы кроются в понятиях предела и непрерывности. В этом параграфе мы разберём, как эти математические идеи связаны с устойчивостью алгоритмов оптимизации, их сходимостью и общей надёжностью решений в задачах анализа данных.
Но начнём мы наше погружение с функций. Это основной инструмент математики, и он широко используется в анализе данных и машинном обучении для моделирования отношений между переменными.
Функции
Функция — это правило, сопоставляющее каждому элементу области определения ровно одно значение из области значений.
Проще говоря, функция принимает на вход некоторое значение и выдаёт соответствующее ему выходное значение. В математике функцию обычно обозначают как , где — входная переменная, а — соответствующее ей выходное значение.
Пример — функция .
Она берёт число (входное значение) и возвращает результат его удвоения (выходное значение).
- Если на вход подать , то функция вернёт .
- Если на вход подать , то функция вернёт .
Это правило связывает каждое входное значение с ровно одним выходным значением, что соответствует определению функции.
Множество входных значений ещё называют
областью определения, а множество выходных значений —областью значений. Дальше мы будем использовать именно эти термины, не теряйтесь!
Вот некоторые типы функций:
|
Тип функции |
Формула |
Пояснения |
Для чего нужна |
Пример |
|
Линейная функция |
|
— коэффициент наклона, — сдвиг |
Моделирование прямой пропорциональности |
Зависимость цены товара от количества. Если , цена растёт, если , падает |
|
Квадратичная функция |
|
, , — константы, |
Моделирование параболических зависимостей |
Затраты на производство товара в зависимости от объёма выпуска |
|
Экспоненциальная функция |
|
— масштаб, — скорость роста или распада, — основание натурального логарифма, |
Описание процессов роста или распада |
Рост популяции бактерий или распад радиоактивных веществ |
|
Логарифмическая функция |
|
, — константы, |
Анализ процессов с затухающей динамикой |
Уровень насыщения в маркетинговых кампаниях: добавление рекламы увеличивает продажи, но с каждым разом эффект от рекламы становится меньше |
|
Гиперболическая функция |
|
— масштаб, |
Моделирование процессов, где результат убывает обратно пропорционально входным данным |
Распределение давления в жидкости по мере удаления от источника |
Функции особенно важны в анализе данных и машинном обучении, поскольку они:
- Позволяют моделировать зависимость между входными признаками и целевой переменной.
- Помогают оценить качество модели (через функцию потерь).
- Лежат в основе алгоритмов оптимизации, которые настраивают параметры моделей, чтобы добиться их наилучшего функционирования.
Но, чтобы эффективно работать с функциями в контексте оптимизации и анализа данных, необходимо понимать, как они ведут себя при изменении входных значений. Это приводит нас к изучению понятий предела и непрерывности — давайте рассмотрим их.
Понятие предела последовательности и функции
В анализе данных и машинном обучении многие алгоритмы работают итеративно, шаг за шагом приближаясь к оптимальному решению. Этот процесс невозможно представить без применения основ математического анализа, где понятие предела играет фундаментальную роль.
Хотя пределы редко применяются напрямую, они служат основой для других важных концепций — непрерывности, производных и интегралов, — которые позволяют описывать поведение алгоритмов, анализировать их сходимость и разрабатывать надёжные методы оптимизации.
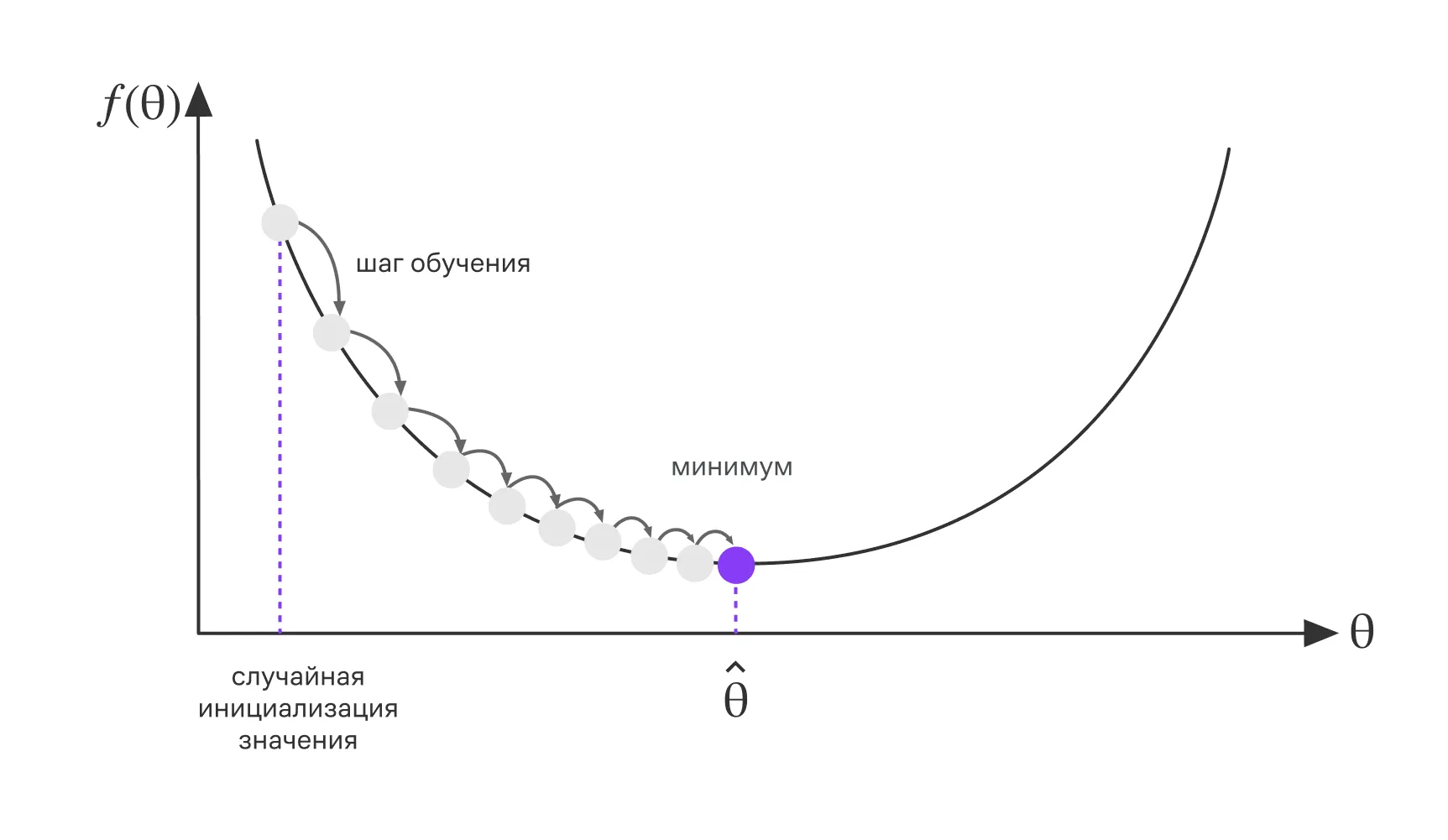
Итеративное обновление параметра методом градиентного спуска
Например, для минимизации функции потерь мы применяем градиентный спуск. Это один из самых распространённых методов оптимизации. Он обновляет параметры модели на каждом шаге, изменяя их значения по направлению наискорейшего убывания функции потерь. Таким образом, параметры модели образуют последовательность значений, которая с каждой итерацией становится всё ближе к оптимальному решению.
Анализ пределов таких последовательностей позволяет оценить, сходятся ли они к желаемому результату, а понятие непрерывности помогает понять, как малые изменения входных данных влияют на выход модели.
Это основа для разработки надёжных, устойчивых и эффективных алгоритмов.
Теперь давайте детальнее посмотрим на определения предела и непрерывности.
Предел последовательности
Предел последовательности — это значение, к которому приближаются элементы последовательности по мере роста их номеров.
Формально последовательность чисел имеет конечный предел (записывают или при ), если для любого сколь угодно малого положительного числа существует такое натуральное число , что для всех выполняется неравенство:
Это означает, что начиная с некоторого номера все члены последовательности находятся в -окрестности числа .
Пример: Рассмотрим последовательность . Покажем, что .
Для любого выберем . Тогда для всех :
Таким образом, данная последовательность сходится к нулю.
В некоторых задачах оптимизации нам потребуется понимание, как функция ведёт себя в окрестности определённой точки, поэтому рассмотрим определение предела функции в точке.
Предел функции в точке
Предел функции описывает поведение её значений при приближении аргумента к определённой точке.
Если значения функции становятся всё ближе к конкретному числу по мере приближения аргумента к , говорят, что функция имеет предел в точке .
С точки зрения строгого определения, функция имеет предел в точке (записывают ), если для любого существует такое , что для всех , удовлетворяющих условию , выполняется неравенство:
Это означает, что значения функции сколь угодно близки к , если достаточно близок к , но не равен .
Пример: Найдем предел .
Пусть . Для любого выберем . Тогда при имеем:
Таким образом, предел существует и равен 5.
Один из примеров применения предела функции в задачах анализа данных — это прогнозирование значений временного ряда на основе предыдущих данных. Предположим, у нас есть модель, предсказывающая среднедневную температуру в зависимости от времени . Если при небольших изменениях времени предсказанное значение меняется совсем незначительно, то при предсказываемая температура приблизится к значению , наблюдаемому в этот момент.
Иными словами, при достаточно малых изменениях значение остаётся близким к , что записывается следующим образом:
где может быть сколь угодно малым.
Но некоторые функции бывают негладкими. Это значит, что у них есть точки разрыва или участки, где невозможно вычислить производную (о производной мы поговорим подробно в следующем параграфе).
Для анализа негладких функций применяются односторонние пределы. Рассмотрим их подробнее.
Односторонние пределы
Когда функция приближается к точке с разных сторон, её поведение может быть различным. Для описания таких ситуаций существуют понятия левостороннего и правостороннего пределов:
- Левосторонний предел — предел функции при , стремящемся к слева ().
- Правосторонний предел — предел функции при , стремящемся к справа ().
Чтобы функция имела предел в точке , левосторонний и правосторонний пределы в этой точке должны существовать и быть равны между собой. В противном случае говорят, что функция имеет разрыв.
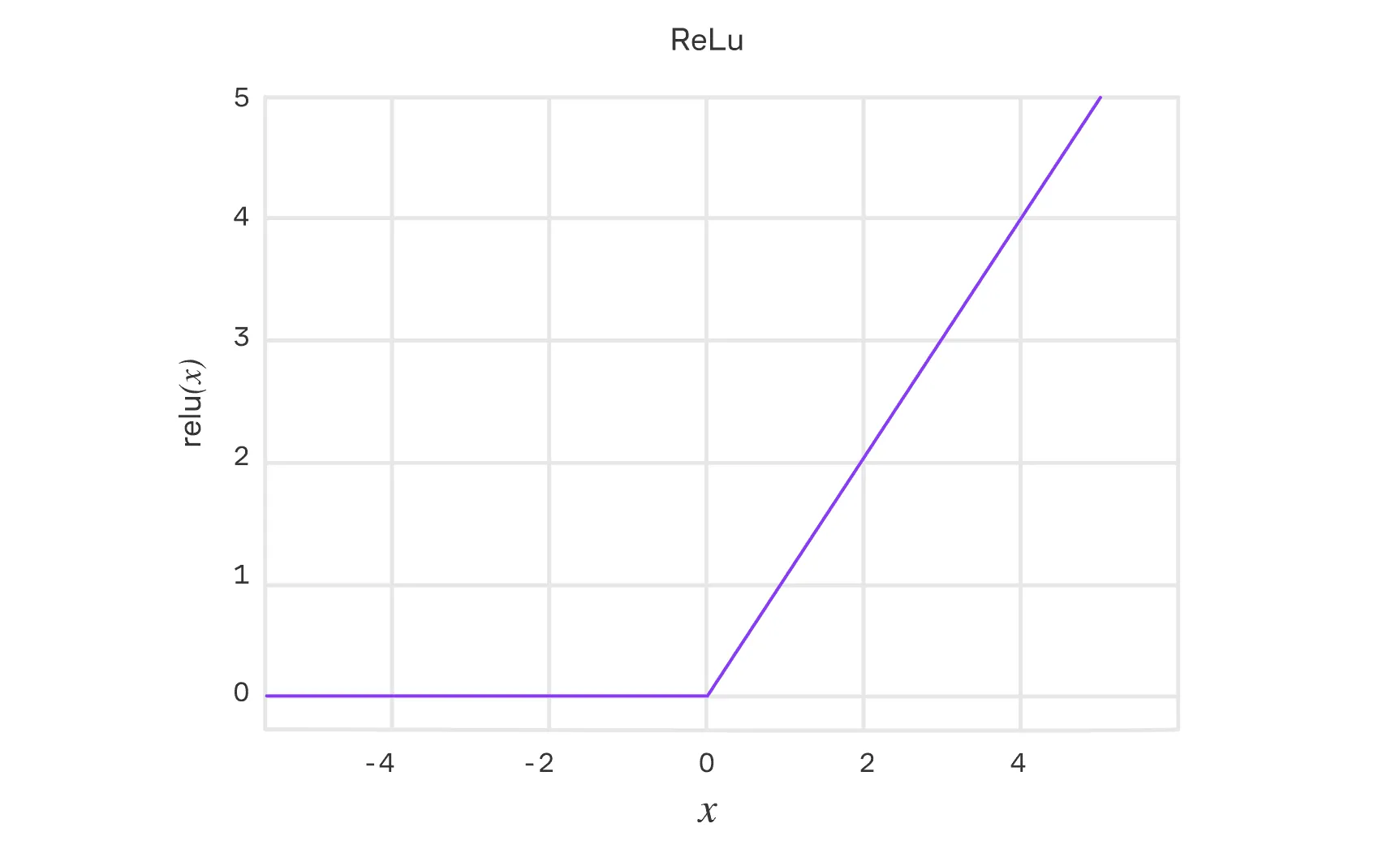
Пример 1: Возьмем функцию активации в нейронных сетях ReLU: . Сама эта функция непрерывна в точке , так как слева и справа пределы совпадают. Однако, если рассматривать её производную как новую функцию, то для неё в точке левосторонний и правосторонний пределы различны ( и соответственно). Значит, у производной в этой точке нет предела, хотя исходная функция остаётся непрерывной.
Пример 2: Рассмотрим функцию ошибки Huber Loss, которая используется для задач регрессии. Она сочетает в себе свойства квадратичной и линейной функций, что делает её устойчивой к выбросам. Вот определение Huber Loss:
Где:
- — разница между истинным значением и предсказанием модели .
- — параметр, определяющий область перехода между квадратичной и линейной частями функции (порог).
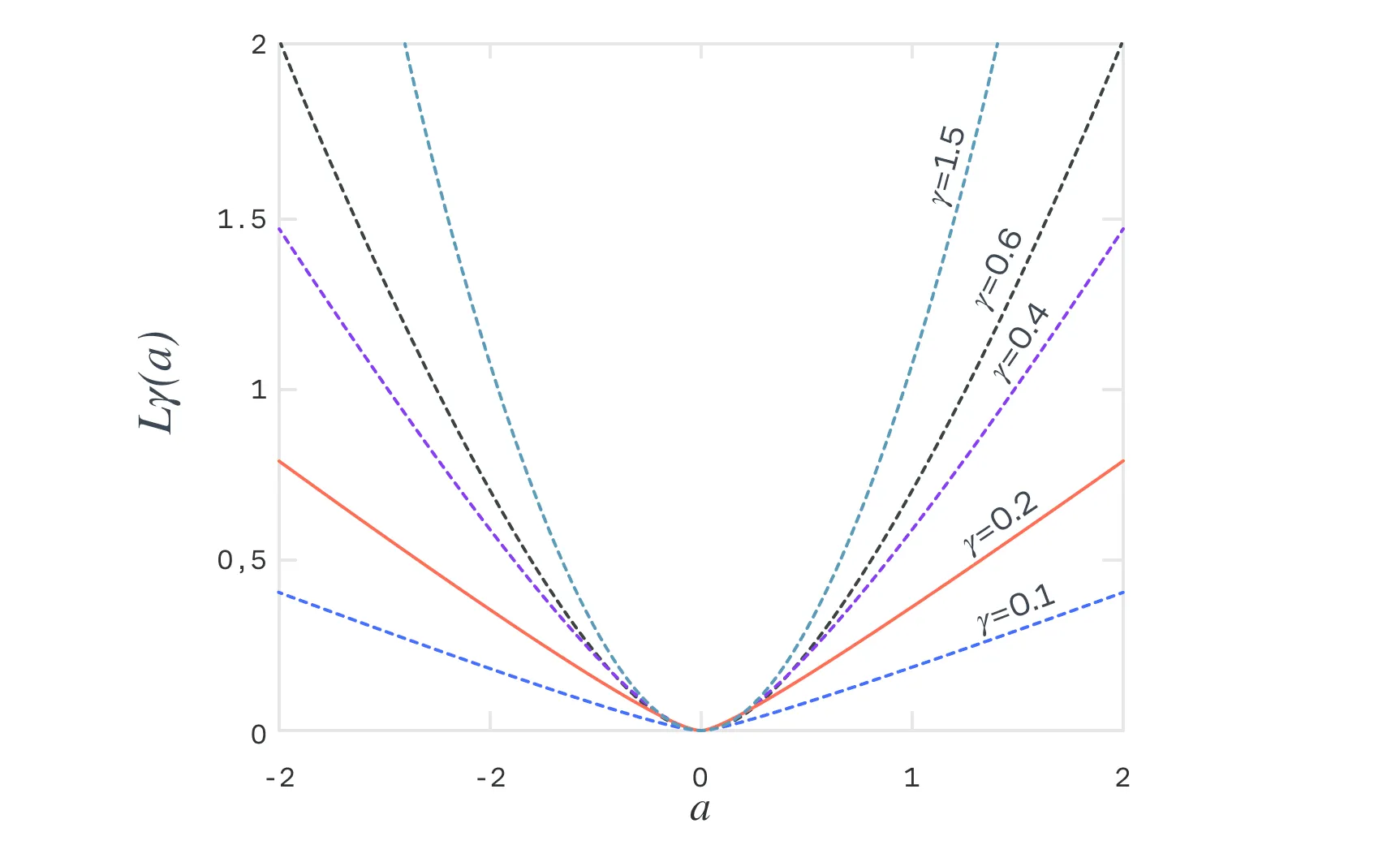
Давайте проанализируем функцию:
- При функция ведет себя как квадратичная функция потерь , что обеспечивает чувствительность к небольшим ошибкам и позволяет эффективно минимизировать малые отклонения.
- При функция становится линейной , снижая влияние крупных ошибок (выбросов) и делая модель более устойчивой.
В точках и функция Huber Loss остаётся непрерывной и имеет непрерывную первую производную (это показатель скорости изменений). Однако вторая производная испытывает скачок в этих точках, что приводит к излому на графике функции.
- Левосторонняя производная при равна .
- Правосторонняя производная при равна .
Хотя значения первой производной совпадают, вторая производная меняется скачкообразно (с 1 до 0) в точках . Это означает, что функция не является гладкой второго порядка в этих местах, несмотря на непрерывность и дифференцируемость её первой производной.
Благодаря своим свойствам функция ошибки Huber Loss позволяет модели быть более устойчивой к выбросам, сочетая преимущества MSE (Mean Squared Error) и MAE (Mean Absolute Error).
Рассмотрев понятие предела, мы можем перейти к следующему фундаментальному свойству функций — их непрерывности.
Непрерывность и свойства непрерывных функций
Непрерывность обеспечивает стабильность и предсказуемость поведения моделей, позволяя понять, как малейшие изменения входных данных отражаются на результате. Это особенно важно для создания надёжных и эффективных алгоритмов.
Перед тем как углубиться в понятие непрерывности, важно определить ключевые термины, связанные с её практическим применением:
- Стабильность модели — это способность алгоритма давать предсказуемые результаты при небольших изменениях входных данных. Малые возмущения на входе не должны приводить к существенным отклонениям на выходе, что особенно важно в условиях работы с шумными или неидеальными данными.
- Устойчивость модели — это её способность сохранять точность и производительность даже при наличии шума, выбросов или изменений в данных. Устойчивая модель демонстрирует хорошую обобщающую способность на новых данных и не склонна к переобучению.
- Предсказуемость модели — это её способность выдавать результаты, которые интуитивно или математически согласуются с изменениями входных данных. Например, если модель прогнозирует температуру на основе времени суток, мы ожидаем, что небольшое изменение времени не приведёт к резким скачкам температуры, как если бы предсказания показывали +30°C на рассвете и –10°C через минуту. Предсказуемость повышает доверие к модели.
Эти понятия служат основой для понимания важности непрерывности функций в математическом анализе и их роли в машинном обучении. Вернемся теперь к понятию непрерывности.
Интуитивно функция называется непрерывной в точке, если небольшие изменения аргумента приводят к небольшим изменениям значения функции. Другими словами, функция ведёт себя предсказуемо, без резких скачков, в каждой точке своей области определения.
Более формально функция называется непрерывной в точке , если выполняются два условия:
- Существует значение .
- Существует предел , и он равен значению функции в этой точке: .
Если хотя бы одно из этих условий нарушается, функция называется разрывной в точке .
Рассмотрим пример функции потерь, которая естественным образом возникает в задачах бинарной классификации. Пусть , где — истинное значение целевой переменной, а — предсказание модели. Определим функцию потерь следующим образом:
В интерпретации задач классификации, если предсказание совпало с истиной (), потери равны нулю, иначе — единице. Несмотря на свою интуитивную понятность, такая функция потерь не подходит для оптимизации, так как её производная в точках разрыва не определена.
Получается проблема: градиентный спуск и другие оптимизационные методы не смогут корректно обновлять параметры модели. Чтобы обойти её, разрывные функции заменяют непрерывными аппроксимациями, которые сохраняют общий смысл задачи, но позволяют использовать математические методы.
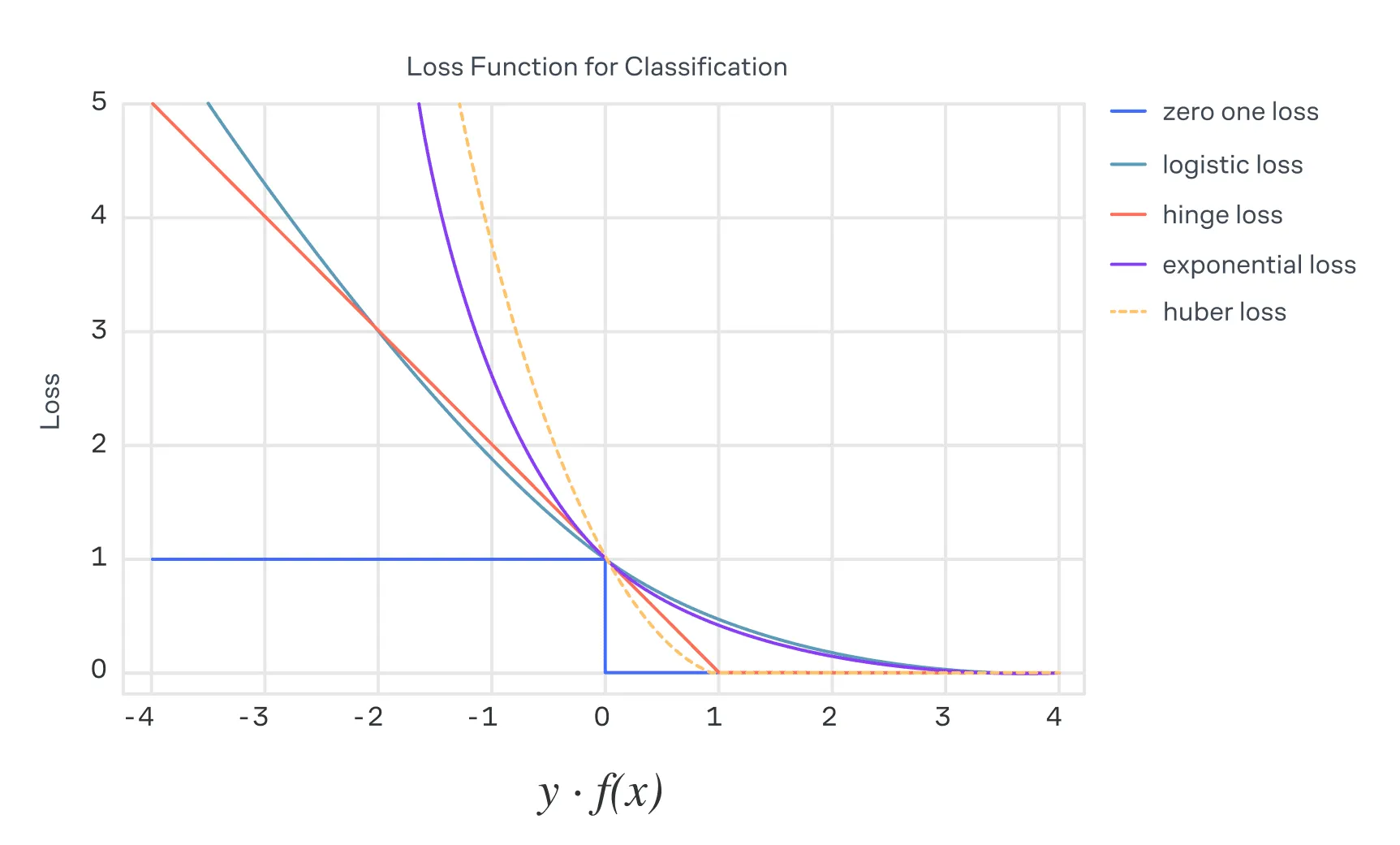
Рассмотрим одну из функций потерь, на которую заменяют ступенчатую функцию в задачах бинарной классификации, — логистическую функцию:
Почему запись именно такая
Этот вид записи эквивалентен более привычной форме логистической функции, представляемой через сигмоиду , где — логарифм от знаменателя . Такая запись часто используется в задачах оптимизации, так как она упрощает вычисления градиентов.
Эта функция — гладкая, что позволяет эффективно использовать градиентный спуск. Использование таких функций для решения задач оптимизации делает задачу не только решаемой, но и вычислительно более эффективной.
Познакомимся с основными свойствами непрерывных функций:
- Арифметические операции. Если функции и непрерывны в точке , то их сумма, разность, произведение и частное (при ) также будут непрерывны в этой точке. Это свойство делает возможным построение сложных моделей из простых компонентов.
Пример: В нейронных сетях непрерывность сохраняется на всех уровнях благодаря тому, что линейные преобразования и функции активации (например, уже известная нам ReLU) являются непрерывными.
-
Составные функции. Если непрерывна в точке , а непрерывна в и , то составная функция также непрерывна в .
-
Теоремы о непрерывности:
- Больцано — Коши. Если функция непрерывна на отрезке и значения на концах отрезка имеют противоположные знаки (), то существует хотя бы одна точка , где . Эта теорема лежит в основе методов численного поиска корней уравнений.
- Вейерштрасс. Непрерывная функция на отрезке достигает своего максимума и минимума. Это свойство важно, например, для определения границ значений в задачах оптимизации.
Когда мы говорим о непрерывных функциях, важно помнить, что непрерывность сама по себе не накладывает ограничений на скорость изменения функции. Функция может быть непрерывной, но при этом резко меняться, что может вызвать сложности в задачах оптимизации и анализа. Именно здесь на помощь приходит понятие Липшицевой непрерывности, которое вводит более строгий контроль за тем, насколько сильно значения функции могут изменяться в ответ на изменения входных данных.
Липшицева непрерывность
Функция называется непрерывной по Липшицу на множестве , если существует константа , такая, что для любых выполняется:
Липшицева непрерывность — более строгая форма непрерывности, которая ограничивает скорость изменения функции. Это свойство важно для анализа сходимости и устойчивости алгоритмов.
Почему это важно для нас: Липшицева непрерывность градиента функции потерь позволяет ограничивать шаг обучения в градиентном спуске, обеспечивая стабильность и быструю сходимость алгоритма, то есть уменьшение числа итераций, необходимых для достижения заданного уровня точности.
В алгоритмах оптимизации градиентного спуска с адаптивным шагом мы будем использовать именно предположение о непрерывности по Липшицу — чтобы обеспечить корректное поведение.
Теперь рассмотрим пример, где градиент функции не является Липшицевым на всей области определения, но становится таким при ограничении интервала — это позволит лучше понять, как непрерывность по Липшицу зависит от области анализа.
Возьмем функцию: , где градиент функции:
Проверим непрерывность градиента по Липшицу:
Для функции градиент не ограничен на всей числовой прямой, поэтому он не является непрерывным по Липшицу на . Однако если мы ограничим область определения, например, интервалом , то можем найти константу Липшица на этом интервале.
Допустим, рассматриваем .
Тогда для любых :
Таким образом, на интервале градиент функции является непрерывным по Липшицу с константой .
Константа Липшица: .
Как мы нашли константу Липшица?
В данном случае мы воспользовались свойством, что если функция дважды дифференцируема и её вторая производная ограничена, то градиент функции является Липшицевым с константой, равной максимальному значению второй производной.
Для функции :
- Первая производная (градиент):
- Вторая производная:
На интервале :
-
Максимальное значение второй производной:
Как итог:
- Градиент является Липшицевым с константой .
Выберем шаг обучения: .
Итеративное обновление:
Сходимость:
Поскольку функция выпукла и её градиент Липшицев с константой на отрезке , последовательность будет сходиться к точке минимума на этом интервале.
Однако заметим, что функция не имеет глобального минимума на , так как она неограниченно возрастает при и стремится к нулю при . Поэтому градиентный спуск будет стремиться к .
Данный пример демонстрирует важный факт:
Сходимость градиентного спуска не требует глобальной непрерывности градиента по Липшицу на всей области определения функции. Достаточно, чтобы градиент обладал этим свойством локально, в окрестности оптимального решения.
Ведь на практике множество задач оптимизации предполагает, что искомый минимум функции лежит в некоторой компактной области, где условия Липшица выполняются. Например, если шаг обучения выбран из интервала , где — локальная константа Липшица для градиента, то градиентный спуск будет сходиться к минимуму, даже если глобальная непрерывность градиента по Липшицу нарушается.
Применение этого подхода:
- Вместо работы с глобальной областью достаточно сосредоточиться на компактной области вокруг решения, где выполняются условия гладкости. Это снижает требования к функциям и упрощает анализ.
- В реальных задачах важно понимать, что сходимость алгоритмов оптимизации может быть обеспечена даже для функций, не обладающих глобальной Липшицевой гладкостью, если проблема ограничивается локальной областью, где условия гладкости выполняются.
Другой пример функции, не обладающей непрерывностью по Липшицу
Рассмотрим функцию на интервале .
Анализ:
-
Для и имеем:
-
Разделим это выражение на :
- При значение стремится к бесконечности, что означает, что не существует конечной константы , удовлетворяющей условию Липшица.
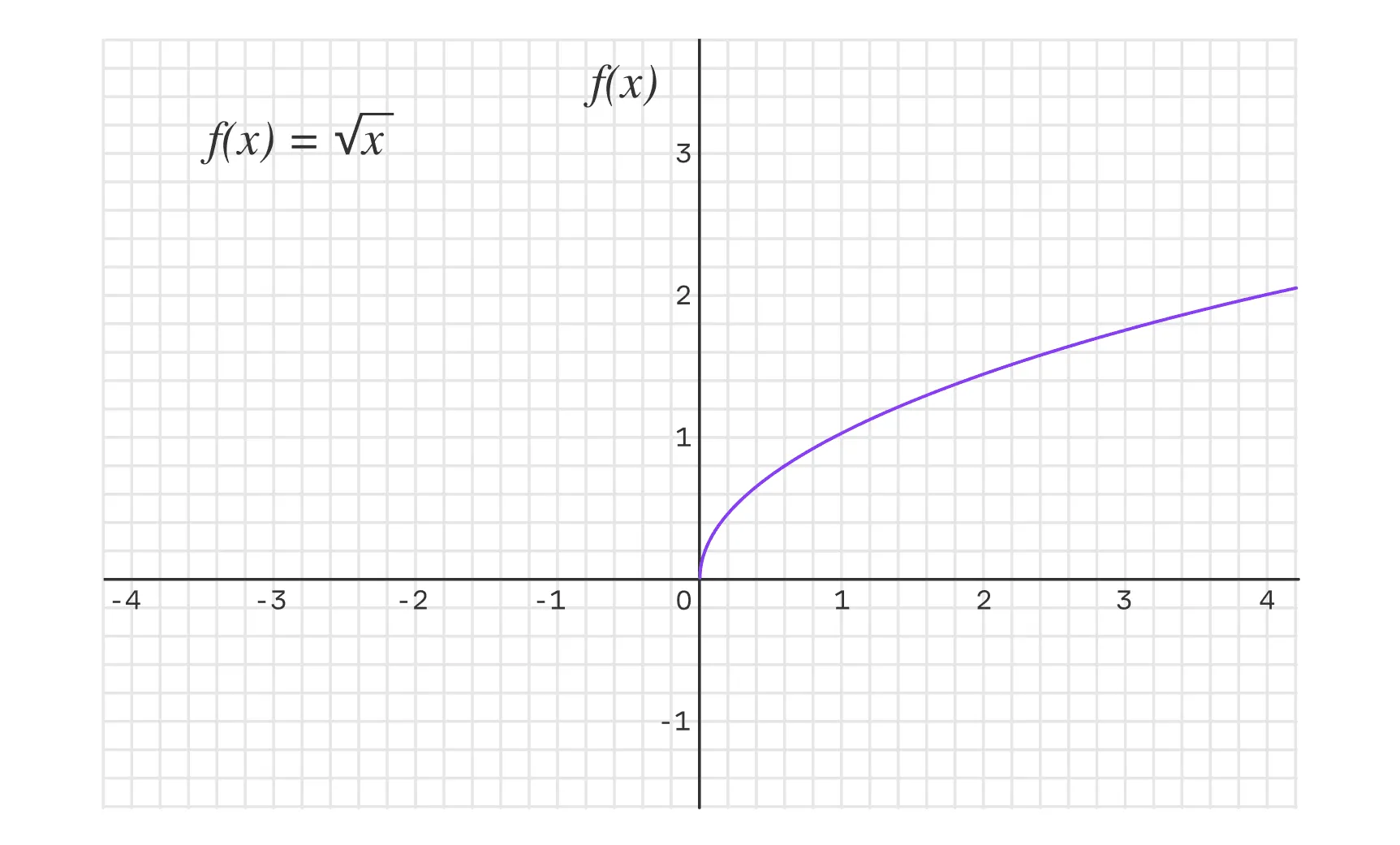
Теперь посмотрим, как реализуется градиентный спуск для нашей функции. Функция определена для , и её градиент (производная) равен . Однако из-за того, что градиент стремится к бесконечности при , градиентный спуск на этой функции может быть нестабильным.
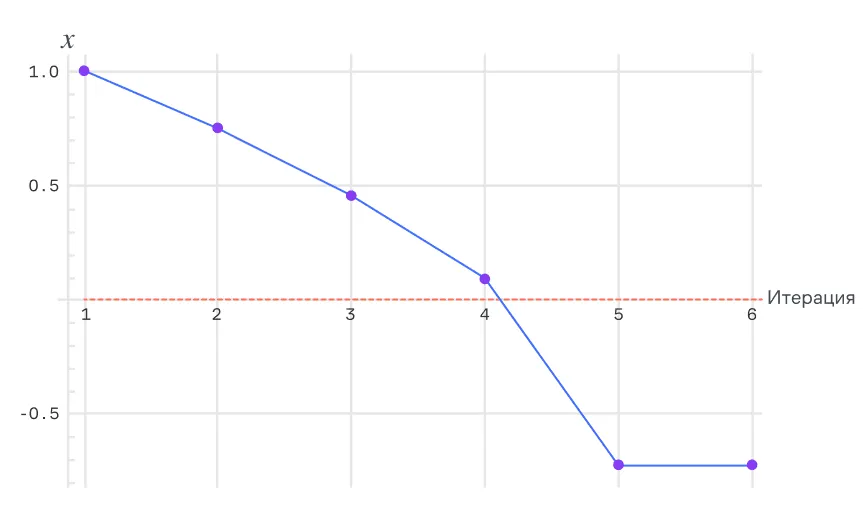
Спуск для
Основная проблема, демонстрируемая на графике, связана с тем, что функция определена только для . Однако в процессе градиентного спуска значение уменьшается и в итоге становится отрицательным, из-за чего дальнейшие вычисления становятся невозможными (градиент перестаёт существовать при ).
Вот что мы видим на графике:
- , расположенный по оси , постепенно уменьшается на каждом шаге (градиентный спуск корректно работает для положительных значений ).
- Критический момент: значение становится отрицательным (пересекает красную линию ), что не соответствует области определения функции .
- После пересечения градиентный спуск не может продолжаться, так как вычисление градиента невозможно.
Градиентный спуск «ломается», потому что:
- Функция не является Липшицевой на всей области, а градиент не определён при .
- Шаг обучения не ограничивает уменьшение до допустимой области.
А теперь пора посмотреть на практическом примере, как концепции предела и непрерывности функции реализуются в анализе сходимости реальных алгоритмов машинного обучения, а также при обеспечении устойчивости моделей.
Анализ сходимости алгоритмов и устойчивости моделей
Итак, давайте представим, что мы решаем задачу машинного обучения, где необходимо найти такие параметры модели, которые минимизируют ошибку предсказания, — это центральная идея большинства алгоритмов. Эти параметры обновляются на каждом шаге, и анализ того, как они ведут себя со временем, помогает понять, действительно ли алгоритм приближается к цели.
Один из наиболее известных подходов — это градиентный спуск, целью которого является минимизация функции потерь . Она показывает, насколько текущая модель далека от истинных значений или реальных меток. Параметры , которые определяют модель, обновляются по следующему правилу:
где:
- — шаг обучения (контролирует размер шага в направлении уменьшения ошибки),
- — градиент функции потерь, указывающий направление возрастания и скорость изменения в текущей точке .
Как видите, здесь важны предел и непрерывность:
- Предел последовательности. Последовательность должна сходиться к оптимальному значению . Анализ сходимости позволяет определить, произойдёт ли это при выбранных условиях (например, при правильном шаге обучения ).
- Непрерывность функции потерь. Если функция непрерывна и её градиент не изменяется резко, алгоритм работает более стабильно и предсказуемо.
Для иллюстрации основного принципа градиентного спуска рассмотрим максимально упрощённую задачу линейной регрессии с одним наблюдением:
- Градиент .
- Итеративное обновление:
В зависимости от значений и мы можем проанализировать сходимость алгоритма. Чтобы сосредоточиться исключительно на анализе, мы возьмём и . При этих значениях задача сводится к следующему:
- Функция потерь: .
- Градиент: .
- Обновление параметра: .
Здесь параметр — это шаг обучения, который контролирует, насколько сильно мы обновляем на каждом шаге. Для того чтобы последовательность параметров сходилась к минимуму функции потерь (), необходимо выполнение условия:
Раскроем это неравенство:
- ,
- .
Таким образом, градиентный спуск сходится к минимуму, если шаг обучения удовлетворяет условию .
Это условие связано с непрерывностью градиента функции потерь . Для текущего примера константа Липшица , что позволяет явно установить границы на . Если выходит за пределы этого диапазона, то обновления параметра становятся слишком резкими и последовательность начинает расходиться.
Анализ сходимости показывает, как алгоритмы оптимизации приближаются к желаемому результату, шаг за шагом минимизируя ошибку. При этом ключевую роль играют пределы и непрерывность: они не только гарантируют, что процесс сходится, но и делают его предсказуемым и стабильным. Однако сходимость — это лишь часть задачи. Чтобы алгоритм был действительно эффективным, важно, чтобы модель оставалась устойчивой, даже если данные содержат шум или небольшие отклонения. Поговорим теперь об устойчивости моделей.
Устойчивость моделей
Устойчивая модель — это модель, результаты которой не меняются кардинально при небольших изменениях входных данных. Например, если мы добавим небольшой шум к нашим данным, устойчивая модель должна выдавать предсказания, которые остаются близкими к исходным.
Как раз здесь мы и можем оценить роль непрерывности:
- Непрерывность функции модели гарантирует, что малые изменения входных данных приводят к небольшим изменениям в предсказаниях модели. Это делает модель предсказуемой и надёжной.
- Если модель обладает
непрерывностью по Липшицу, можно количественно оценить, насколько сильно изменится результат при небольших изменениях на входе.
В этот раз в качестве примера устойчивой модели возьмем линейную регрессию. Функция потерь линейной регрессии включает регуляризационный член , который ограничивает величину параметров модели:
где:
- — вектор признаков,
- — целевая переменная,
- — коэффициент регуляризации.
Регуляризация делает модель устойчивее, так как большие значения параметров подавляются, что предотвращает резкие изменения предсказаний.
В этом параграфе мы увидели, как ключевые понятия математического анализа — пределы и непрерывность — помогают понять и гарантировать сходимость алгоритмов к оптимальному решению. Непрерывность функций и регуляризация способствуют устойчивости моделей, обеспечивая их надёжность даже при наличии шума или отклонений во входных данных.
Теперь, когда мы разобрались с теорией, давайте перейдём к практике. Попробуйте решить задания по этой теме, чтобы закрепить материал и увидеть, как эти концепции работают в реальных задачах.


