При исследовании графов важно не только знать способы их хранения и анализа, но и понимать их особенные характеристики — от этого зависит выбор подходящего для вашей задачи графа.
Рассмотрим, например, граф социальных связей. Если мы выберем группу из пяти случайных людей, перед нами откроются две интересные перспективы:
- Если мы хотим узнать, кто с кем знаком, можно представить людей как вершины графа, а факт знакомства — как рёбра. Такой граф покажет все дружеские связи внутри группы.
- Если же нас интересуют денежные переводы между ними, мы построим ориентированный граф. Здесь вершины будут представлять людей, а рёбра — транзакции, и каждое ребро укажет направление, от кого к кому поступили средства.
Чтобы точнее описать различные сценарии и отношения, давайте разберёмся, как графы классифицируются в зависимости от рёбер, петель, направленности и других характеристик.
Также в этом параграфе мы познакомимся с леммой о рукопожатиях — важным результатом, который связывает структуру графа с его свойствами. Понимание этой леммы позволит глубже разобраться в особенностях различных типов графов и их взаимосвязях.
Классификация №1: по кратным рёбрам и петлям
Первый шаг в классификации графов — анализ наличия кратных рёбер и петель.
Обыкновенный граф — это строгая, упорядоченная структура, где между любыми двумя вершинами может быть не более одного ребра и отсутствуют петли, то есть рёбра, соединяющие вершину саму с собой.
Такой тип графа хорош для ситуаций, где важно учитывать лишь одно отношение между элементами, например в логистическом графе транспортной сети с двусторонними дорогами, где каждая связь между двумя точками представлена единственным ребром.
Если граф допускает кратные рёбра, то он называется мультиграфом. В этом случае между двумя вершинами может быть несколько рёбер, а также разрешаются петли.
Мультиграф подойдёт, если нужно моделировать систему, где может существовать несколько видов связей между одними и теми же элементами. Такие системы включают транспортные сети с различными маршрутами между городами (автобусные, железнодорожные, авиалинии) или компьютерные сети со множеством каналов связи между серверами.
Граф с петлями допускает наличие рёбер, соединяющих вершину саму с собой. Это полезно, когда важно учитывать возможные самоотношения, например обратные связи в системе.
Данные графы применяются, например, в сетях рекомендаций, где петля может указывать на повторное взаимодействие пользователя с одним и тем же объектом (например, заказ любимого блюда в ресторане или повторное приобретение товара).
Пустой граф, в отличие от всех предыдущих, представляет собой структуру без рёбер, состоящую только из изолированных вершин. Здесь каждый элемент автономен и не имеет связей с другими.
Он редко встречается на практике, однако играет важную роль в теории графов — используется при изучении предельных случаев и формулировке общих теорем, где необходимо учитывать все возможные типы графов, включая крайние. То есть пустой граф — это теоретическая модель, а иногда и отправная точка для построения более сложных структур.
Классификация №2: по направленности рёбер
Другая важная характеристика графов — это направленность рёбер. В предыдущем параграфе мы коротко коснулись этой темы, сейчас разберёмся полнее.
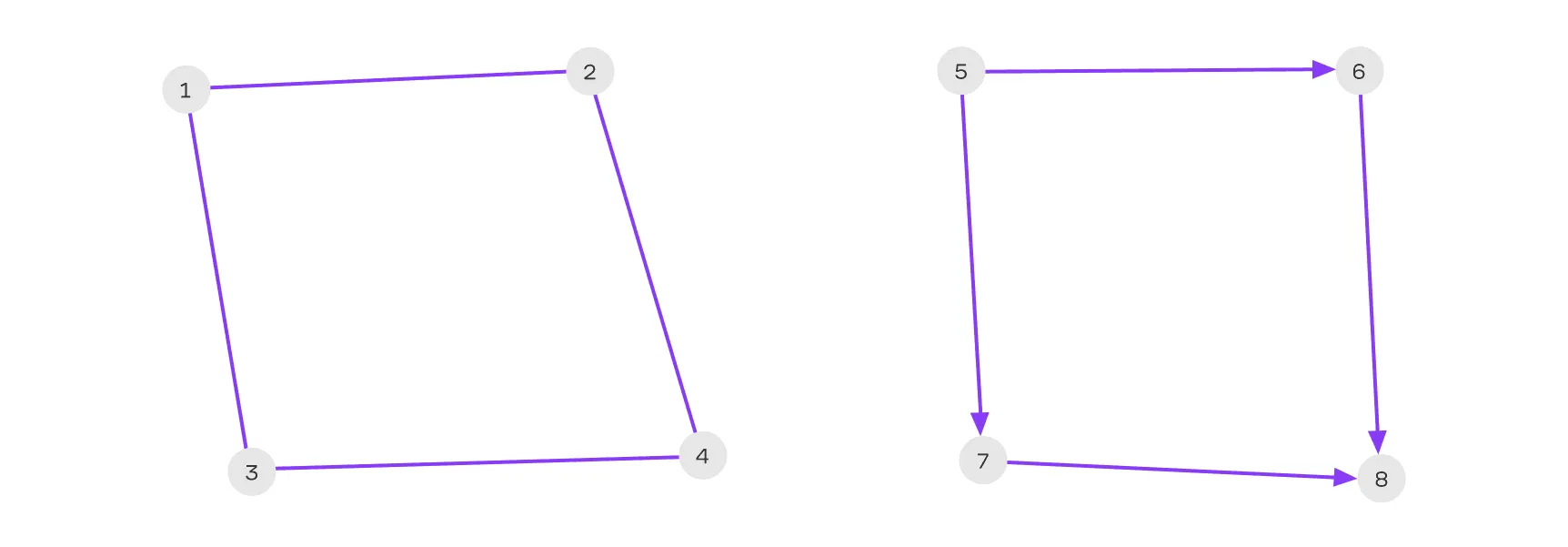
Неориентированный граф — это граф, где рёбра не имеют направления, что делает связь между вершинами двусторонней. Например, если вершина соединена с вершиной , то и связана с , и связана с .
Такие графы удобны для моделирования симметричных отношений, где взаимосвязи равноправны. Например, такую модель можно использовать, чтобы отразить социальный граф знакомств, где связь между двумя людьми указывает на взаимное согласие на общение.
У ориентированного графа, напротив, есть направление рёбер, что делает связи между вершинами односторонними. Если, например, ребро направлено от вершины к вершине , это означает, что связана с , но не наоборот.
Такой граф полезен для направленных взаимодействий. Например, в гейм-дизайне для проектирования сюжетных линий в зависимости от выбора игрока.
Неориентированный граф можно рассматривать как частный случай ориентированного, в котором каждое ребро направлено в обе стороны.
Классификация №3: по связности
Графы также различаются по степени связности.
Связный неориентированный граф — это граф, в котором можно добраться от любой вершины к любой другой по последовательности рёбер. Такой граф образует единую компоненту связности, что полезно в моделях, где каждый элемент связан с другими.
Например, в логистической сети транспортной системы города или пункты доставки представлены вершинами, а дороги между ними — рёбрами. Связный граф в этом случае гарантирует, что из любого города можно доставить груз в любой другой, что важно для эффективного функционирования логистики и оптимизации маршрутов.
В случае сильно связного ориентированного графа каждая вершина достижима из любой другой с учётом направлений рёбер. Примером такого графа может служить система обмена электронными сообщениями внутри организации, где каждый сотрудник может отправить сообщение любому другому сотруднику через внутреннюю почтовую систему.
Здесь узлы — сотрудники, а направленные рёбра — возможность отправки сообщения от одного сотрудника к другому. Сильная связность обеспечивает полную коммуникацию внутри организации.
Слабо связный ориентированный граф — это граф, который становится связным, если его рёбра рассматривать как неориентированные. Иными словами, если игнорировать направления рёбер, вершины будут соединены.
Например, в графе подписок социальных сетей, где узлы представляют пользователей, а направленные рёбра — подписки одного пользователя на другого, такая связность позволяет изучать общую структуру сети через цепочки подписок, образуя связный граф.
Однако важно подчеркнуть, что слабо связный граф не становится сильно связным, поскольку достижимость всех вершин в обоих направлениях в нём не гарантируется.
Вот как выглядят эти графы:
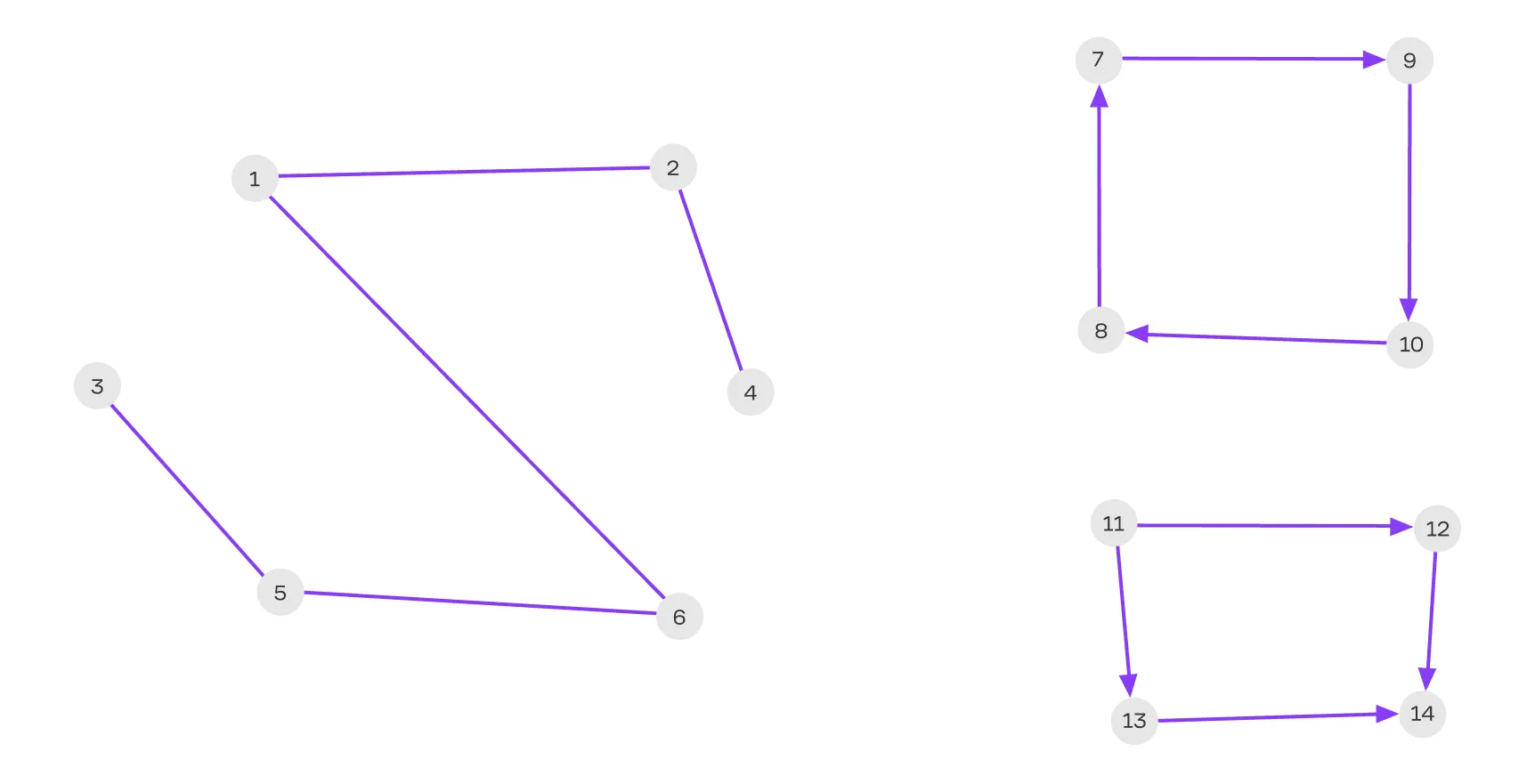
На иллюстрации выше:
- Граф 1–6 — связный неориентированный.
- Граф 7–10 — сильно связный ориентированный.
- Граф 11–14 — слабо связный ориентированный.
Классификация №4: по полноте
Мы коснулись полноты в предыдущем параграфе. Давайте чуть углубимся.
Полные графы — это графы, в которых каждая пара различных вершин соединена рёбрами. В полном неориентированном графе каждая пара вершин соединена ровно одним ребром, что создаёт максимально плотную структуру, где каждая вершина напрямую связана с любой другой.
В контексте анализа данных полный граф может использоваться для отображения всех возможных связей между объектами, например для вычисления попарных расстояний или сходства между элементами в задаче кластеризации.
В полном ориентированном графе каждая пара различных вершин соединена двумя рёбрами, направленными в противоположные стороны. Такое построение позволяет каждой вершине иметь прямую и обратную связь с любой другой.
Полные ориентированные графы могут быть полезны для моделирования систем, где важно учитывать двусторонние взаимодействия между всеми элементами: допустим, в сети финансовых потоков такая структура может отображать движение средств между узлами (компаниями, банками или регионами), где каждая вершина связана с любой другой как отправителем, так и получателем. Это помогает анализировать максимальные потоки, баланс транзакций и выявлять ключевые точки концентрации финансовых ресурсов.
Теперь, разобрав основные типы графов и их классификации, рассмотрим одно из фундаментальных свойств графов — лемму о рукопожатиях.
Это полезный инструмент — она позволяет быстро определить общее количество связей в графе по количеству связей каждого элемента. Зная это, мы можем получить другие данные или проверить правильность нашего графа.
Давайте посмотрим, как это работает в реальной ситуации.
Лемма о рукопожатиях
Представьте вечеринку, где каждый гость поочерёдно здоровается с остальными гостями. Сколько всего рукопожатий между ними произошло? Чтобы ответить на этот вопрос, представим гостей как вершины графа, а рукопожатия между ними — как рёбра, соединяющие вершины.
Лемма о рукопожатиях утверждает, что сумма степеней всех вершин графа всегда равна удвоенному числу его рёбер. Это значит, что, чтобы найти количество рукопожатий на вечеринке, нужно сложить количество рукопожатий каждого гостя и разделить на 2 — потому что каждое рукопожатие учитывается дважды: по одному разу для каждого из участников.
Формально это можно записать следующим образом:
, где:
- — степень вершины , то есть количество рёбер, соединяющих эту вершину с другими;
- — это сумма степеней всех вершин;
- — удвоенное число рёбер графа.
Это выражение показывает, что сумма степеней всех вершин графа всегда является чётным числом, так как каждое ребро добавляет ровно по единице к степени двух вершин, которые оно соединяет.
Попробуйте самостоятельно посчитать сумму степеней вершин и удвоенное количество рёбер для любого графа. Вот небольшой пример в Python с библиотекой networkx:
1import networkx as nx
2import random
3
4random.seed(42) # Фиксируем состояние для воспроизводимости
5graph = nx.erdos_renyi_graph(10, 0.3) # Создаём случайный граф с 10 вершинами и вероятностью ребра 0.3
6
7# Считаем сумму степеней всех вершин
8sum_degrees = sum(dict(graph.degree()).values())
9
10# Считаем удвоенное количество рёбер
11double_edges = 2 * graph.number_of_edges()
12
13print(f"Сумма степеней: {sum_degrees}") # должно получиться 34
14print(f"Удвоенное количество рёбер: {double_edges}") # должно получиться 34
В этом примере мы создаём случайный граф, а затем считаем сумму степеней его вершин и удвоенное количество ребер, которые оказываются равны, что и подтверждает лемму о рукопожатиях.
Доказательство леммы о рукопожатиях
Для наглядности рассмотрим сначала пустой граф — граф без рёбер. В таком графе сумма степеней всех вершин равна нулю. При добавлении нового ребра степень каждой из двух инцидентных ему вершин увеличивается на единицу. Это значит, что общая сумма степеней возрастает на два.
Таким образом, добавление каждого ребра в граф увеличивает сумму степеней на два, что в итоге и приводит к удвоенному количеству рёбер.
Следствие из леммы о рукопожатиях
Одним из важных выводов из этой леммы является следующее утверждение:
В любом графе число вершин нечётной степени является чётным.
Это следствие логически вытекает из формулы: так как сумма степеней всех вершин чётна, то и число вершин, имеющих нечётные степени, также должно быть чётным.
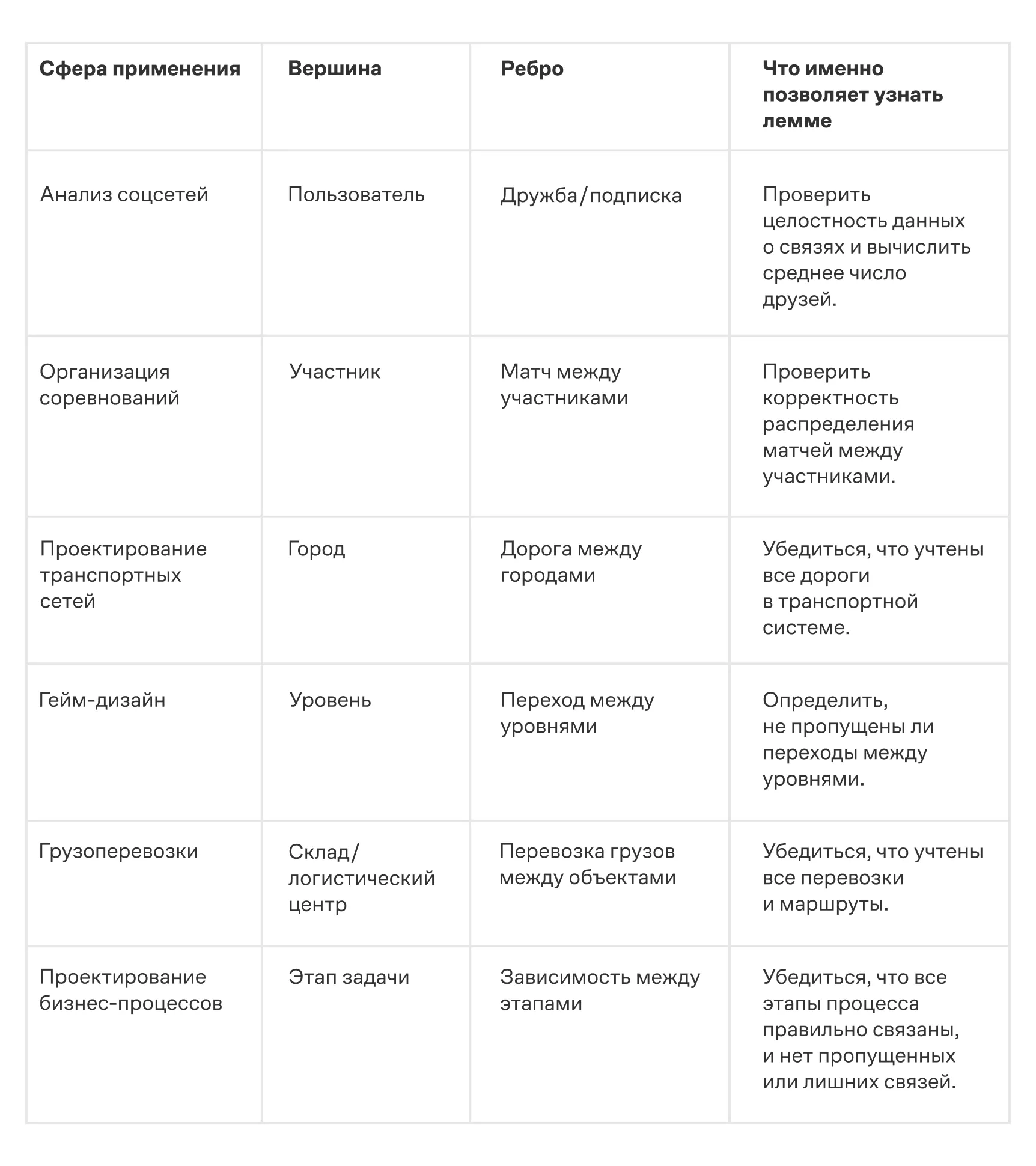
Прежде чем двинуться дальше — вот небольшая таблица о том, в каких сферах может пригодиться лемма о рукопожатиях:
Теперь, когда мы познакомились с основными свойствами графов и леммой о рукопожатиях, перейдём к изучению двудольных графов — особого типа графов с интересной структурой, который применяется в различных областях, от алгоритмов поиска до моделирования систем.
Двудольные графы
Двудольный граф — это граф, в котором все вершины можно разделить на две группы, или доли, так, что рёбра соединяют только вершины из разных долей.
В двудольном графе не существует рёбер, которые соединяли бы вершины внутри одной и той же доли. Это свойство двудольных графов делает их легко распознаваемыми и структурно простыми.
Представьте себе двудольный граф в роли большой торговой площадки, где покупатели и товары разошлись по двум лагерям. Каждый покупатель соединён с теми товарами, которые он добавил в корзину, образуя рёбра графа — своего рода «покупательские следы». Подобный граф отлично показывает, кто что купил, и помогает найти популярные товары, к которым тянутся многие покупатели.
Или другой пример: университет. Одна доля графа — это студенты, а другая — курсы, и рёбра связывают студентов с теми курсами, на которые они записались. Такой граф помогает увидеть, какие курсы наиболее востребованы и как распределяются интересы студентов.
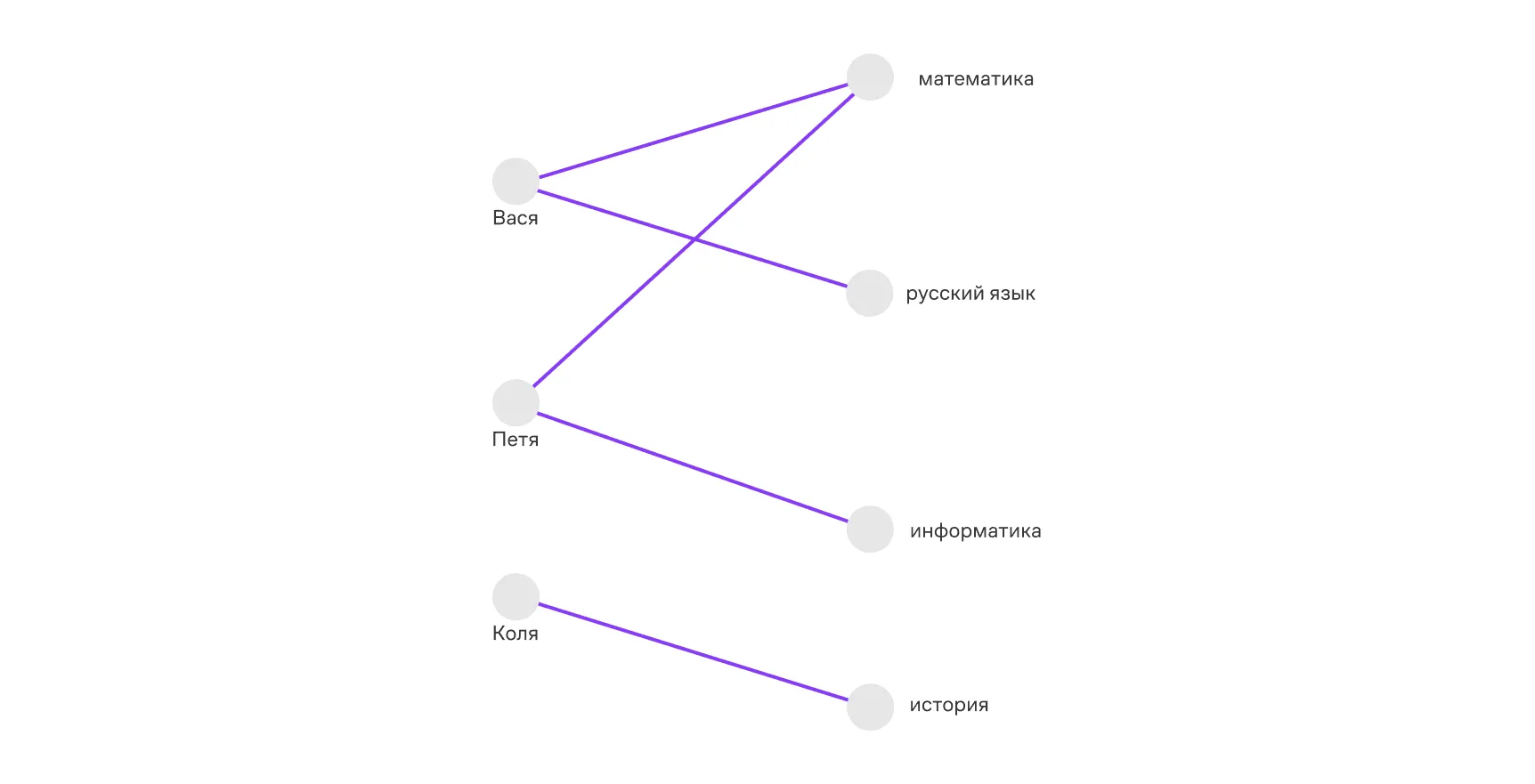
Для наглядного представления двудольного графа часто используется графическая визуализация, где вершины каждой доли располагаются на отдельной прямой линии. Такая схема позволяет сразу увидеть, какие вершины принадлежат каждой доле и как они связаны между собой.
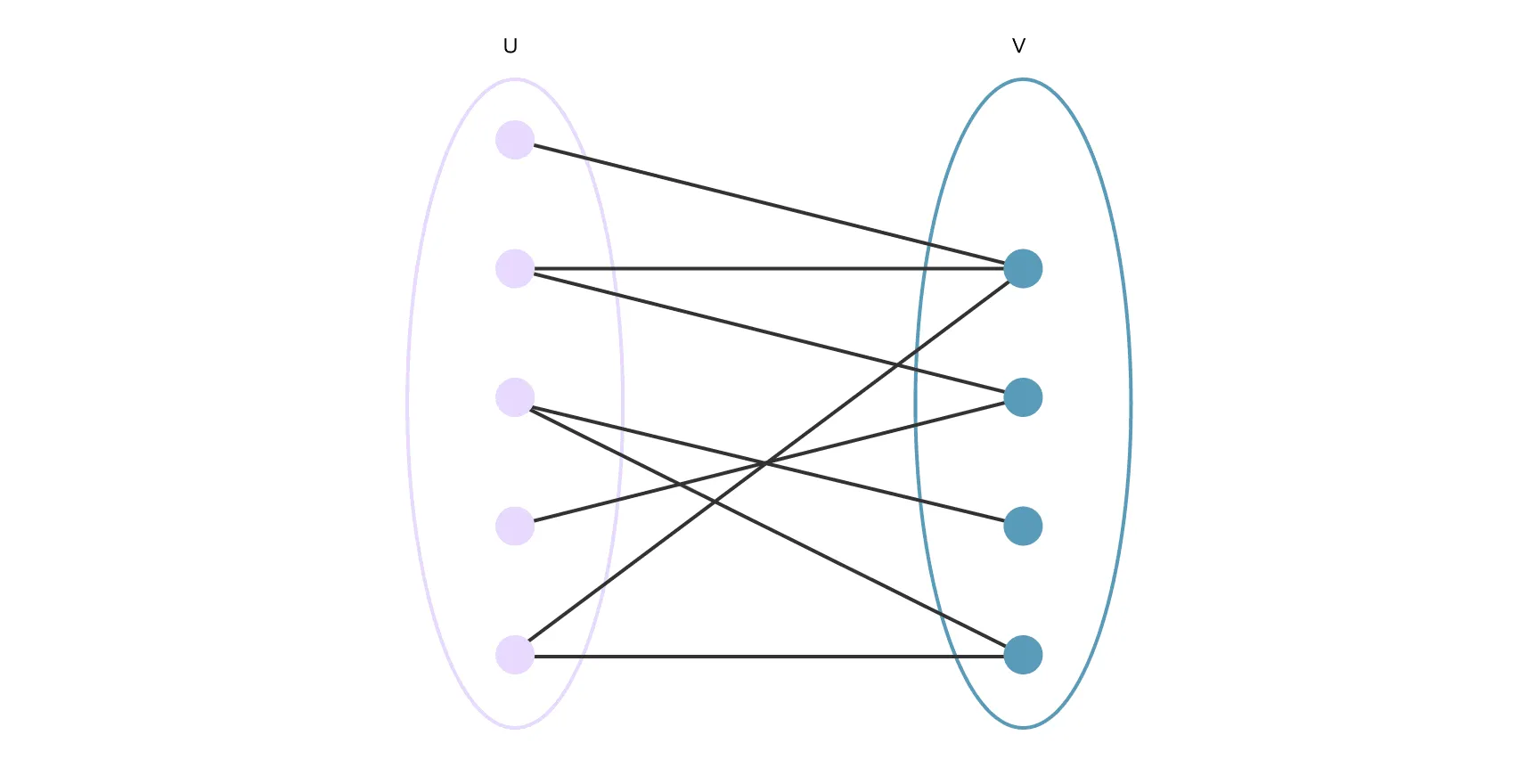
А чтобы и без красивой иллюстрации понять, что перед вами именно двудольный граф, можно воспользоваться теоремой Кёнига. Давайте разберём её подробнее.
Теорема Кёнига
Эта теорема гласит, что граф является двудольным тогда и только тогда, когда в нём нет циклов вообще или нет циклов нечётной длины. Это свойство удобно использовать при анализе графа, так как проверка на отсутствие нечётных циклов позволяет быстро определить, является ли граф двудольным.
Теорему Кёнига можно объяснить следующим образом:
- Если граф двудольный, то в нём действительно не может быть циклов нечётной длины. Представьте, что мы начинаем обход цикла с вершины одной доли и переходим по рёбрам к вершинам другой доли. Чтобы вернуться в начальную вершину, мы должны пройти чётное количество рёбер, и, следовательно, цикл будет чётным.
- Если в графе нет циклов нечётной длины, то его можно разделить на две доли. Для доказательства этого можно использовать метод раскраски: раскрасьте вершины графа в два цвета (например, чёрный и белый), так чтобы соседние вершины всегда имели разные цвета. Если в графе нет циклов нечётной длины, такая раскраска будет успешной, и граф можно будет считать двудольным.
Строгое доказательство теоремы Кёнига
Утверждение: Граф является двудольным тогда и только тогда, когда все циклы в графе имеют чётную длину.
Доказательство:
-
Необходимое условие
Пусть граф — двудольный. Разделим его вершины на две доли, обозначенные и , где рёбра могут соединять вершины только из разных долей. Если мы начнём обход цикла с некоторой вершины в доле , то каждый шаг, представляющий ребро, переносит нас из одной доли в другую. Следовательно, чтобы вернуться в начальную вершину, нам нужно пройти чётное количество рeбер, поскольку каждый переход переносит нас в противоположную долю. Таким образом, любой цикл в двудольном графе имеет чётную длину. -
Достаточное условие
Пусть теперь граф не содержит циклов нечётной длины. Выберем произвольную вершину и определим её как начальную. Разделим все вершины графа на два множества: , содержащее вершины, которые находятся на чётном расстоянии от , и , содержащее вершины, которые расположены на нечётном расстоянии от (если расстояние определяется минимальным числом рёбер). Такое разбиение гарантирует, что и включает все вершины графа.
Теперь, допустим, что существует ребро, соединяющее две вершины внутри одной доли, например вершины и в . Пусть — кратчайший путь от до и — кратчайший путь от до . Поскольку обе вершины находятся в , длины путей и будут чётными. Если теперь соединить эти пути ребром , то получится цикл, длина которого также будет нечётной, что противоречит предположению об отсутствии нечётных циклов. Аналогичное рассуждение верно и для вершин в .
Теорема Кёнига важна для понимания структуры двудольных графов, так как она позволяет легко проверять двудольность графа с помощью анализа циклов. Это свойство лежит в основе многих алгоритмических приложений. Например:
- Паросочетания в задачах распределения ресурсов. Представьте компанию, которая хочет распределить сотрудников (одна доля графа) на проекты (другая доля графа) так, чтобы максимально учесть предпочтения сотрудников и требования проектов. Двудольный граф здесь позволяет применять алгоритмы нахождения максимального паросочетания, эффективно решая задачу.
- Оптимальное разбиение в логистике. Например, при организации распределительных центров, где точки доставки и склады представляют собой две доли графа. Оптимальное разбиение помогает минимизировать транспортные расходы, создавая сбалансированные маршруты между складами и клиентами.
Теперь рассмотрим подробнее несколько видов двудольных графов.
Полный двудольный граф
В таком графе каждая вершина одной доли соединена с каждой вершиной другой доли. Он обозначается как , где и — это количество вершин в каждой из долей.
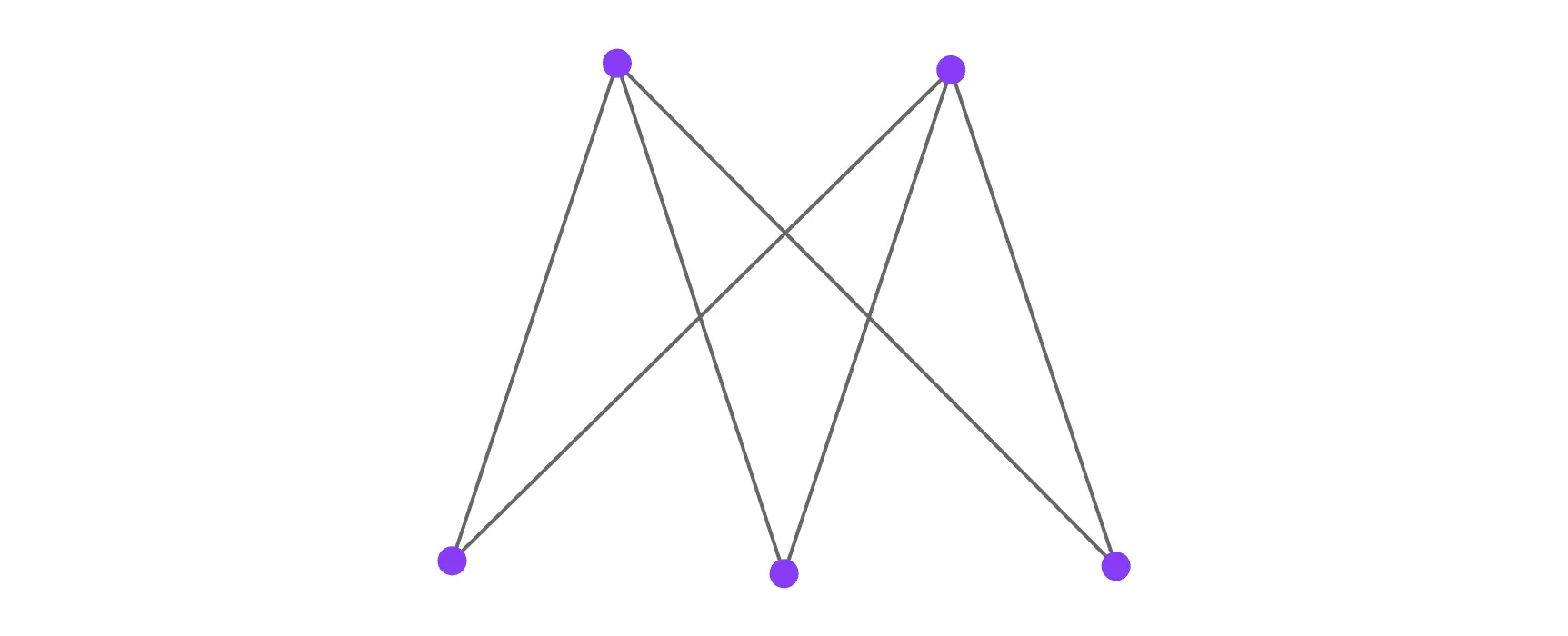
Например, — это граф, где одна доля содержит 2 вершины, а другая — 3 вершины. Граф представляет собой звезду, где одна центральная вершина соединена со всеми вершинами другой доли. В полном двудольном графе содержится рёбер и каждая вершина имеет степень, равную количеству вершин в другой доле.
Бинарное дерево
Это особый вид двудольного графа, в котором каждая вершина имеет не более двух потомков и не содержит циклов. В бинарных деревьях существуют понятия корня (вершина, не имеющая предков), листьев (вершины без потомков) и узлов (все остальные вершины). Деревья — это важная структура в информатике, особенно в алгоритмах сортировки, поиска и сжатия данных.
Хотя двудольные графы могут быть различными по форме, все деревья, независимо от количества потомков у каждой вершины, тоже считаются двудольными графами.
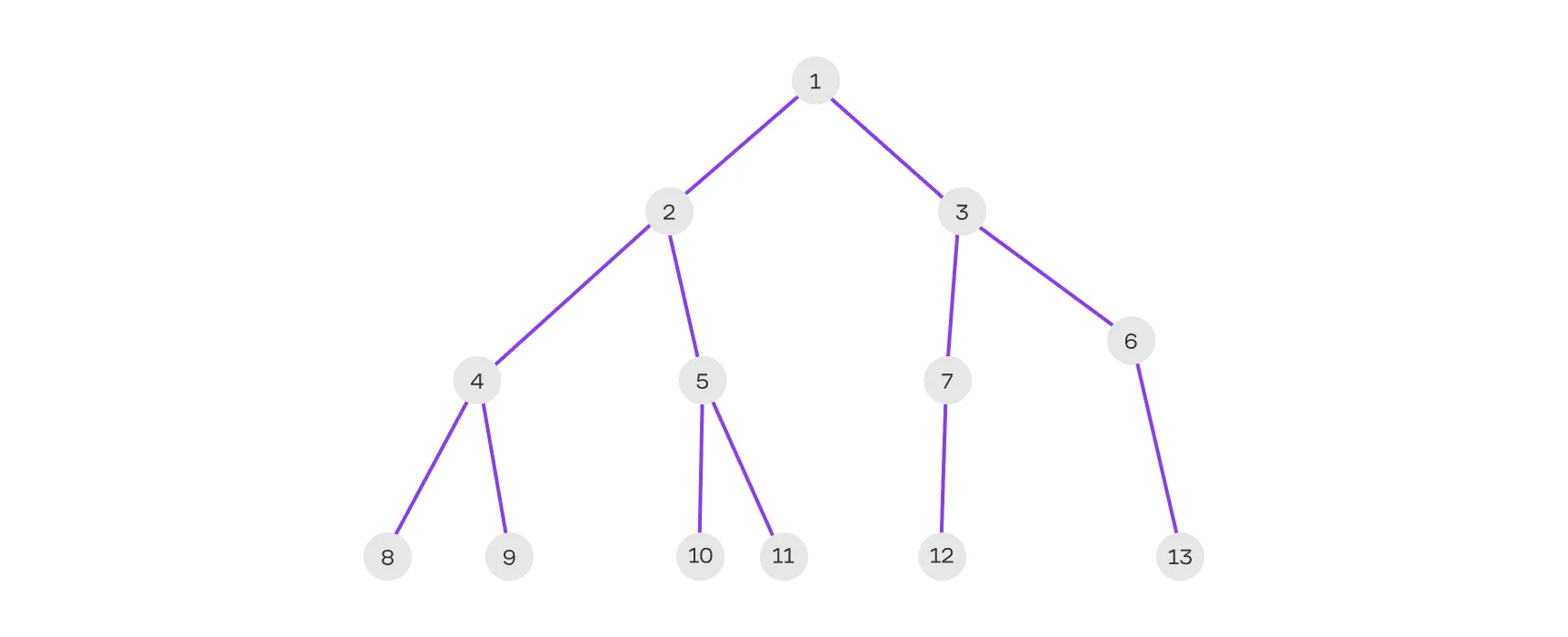
На иллюстрации выше: вершина 1 — это корень, 8–13 — листья, 2–7 — узлы.
В этом разделе мы рассмотрели основные типы графов, лемму о рукопожатиях и свойства двудольных графов. Эти концепции формируют базис для анализа графов и поиска оптимальных решений в задачах, связанных с сетями и структурами данных.
Закрепим эти знания на практике c помощью задач, которые демонстрируют применение теории графов в реальных примерах.
Объяснение
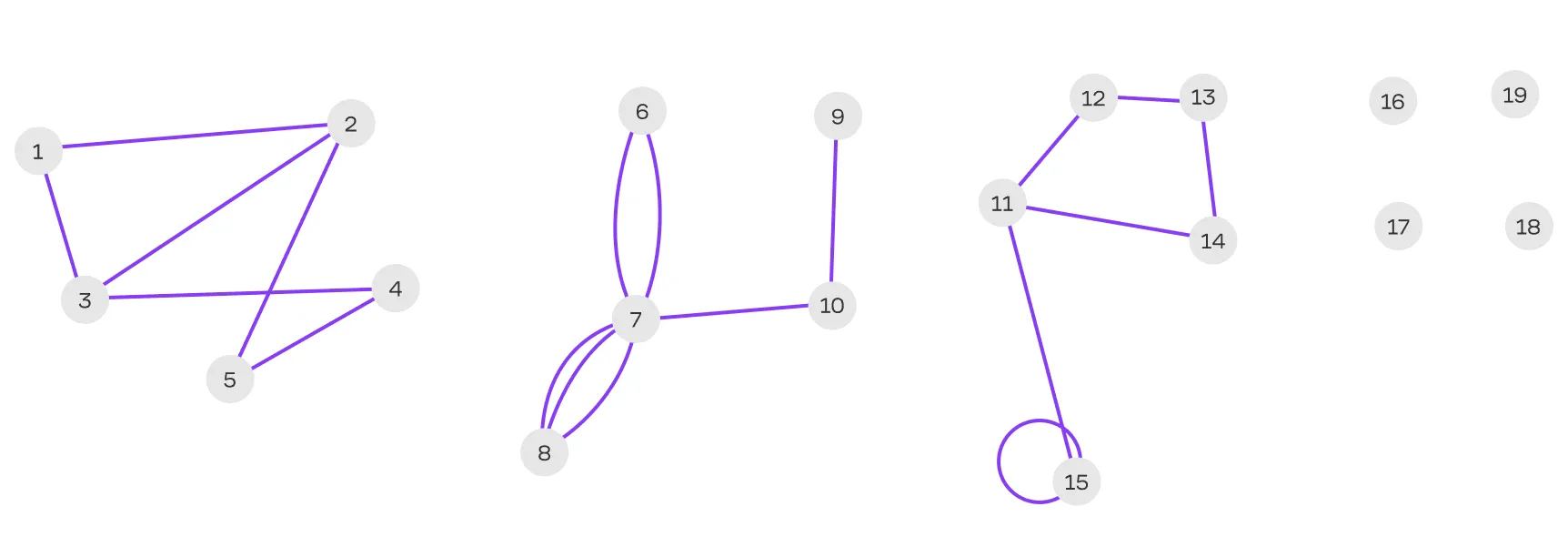
- Граф не является обыкновенным, так как содержит петлю в вершине 1 и кратное ребро между вершинами 4 и 5.
- Граф является мультиграфом, так как содержит кратное ребро.
- Граф содержит петли.
- Граф является неориентированным, так как рёбра не имеют направления.
- Граф является связным, так как все вершины достижимы друг от друга.
- Граф не является сильно связным и слабо связным, так как эти понятия применимы только к ориентированным графам, а данный граф является неориентированным.
Объяснение
В социальной сети любые пользователи могут быть связаны друг с другом, что нарушает принцип двудольности.
Объяснение
Полный двудольный граф может быть использован для отображения всех возможных сочетаний ресторанов и желаемых блюд, что полезно для поиска.
Объяснение
Граф является двудольным, потому что все вершины разделены на две группы (пользователи и рестораны) и рёбра соединяют только вершины из разных групп.
Пример программы на Python для визуализации такого графа:
1import networkx as nx
2import matplotlib.pyplot as plt
3
4# Создаём граф
5G = nx.Graph()
6
7# Добавляем вершины
8G.add_nodes_from(['A1', 'A2', 'A3', 'B1', 'B2', 'B3'])
9
10# Добавляем рёбра
11G.add_edges_from([('A1', 'B1'), ('A1', 'B2'), ('A1', 'B3'), ('A2', 'B2'), ('A2', 'B3'), ('A3', 'B2'), ('A3', 'B3')])
12
13# Определяем цвета для вершин
14node_colors = ['red' if node.startswith('A') else 'blue' for node in G.nodes]
15
16# Рисуем граф
17nx.draw(G, with_labels=True, node_color=node_colors)
18
19# Отображаем граф
20plt.show()




