2.4. Деревья в теории графов

Представьте себе организационную схему крупной компании. В самом верху будет руководитель, чуть ниже — его заместители, затем — главы департаментов и подчинённые им главы отделов. В самом низу — линейные сотрудники.

В мире графов такие схемы называются деревьями. Они выделяются своей уникальной структурой: деревья не содержат циклов, всегда связны и имеют ровно на одно ребро меньше, чем вершин.

Эти свойства делают деревья чрезвычайно удобными для задач, где важно избежать избыточности и построить оптимальные связи. Именно поэтому деревья заслуживают отдельного внимания как одна из ключевых моделей в теории графов.

Типы деревьев

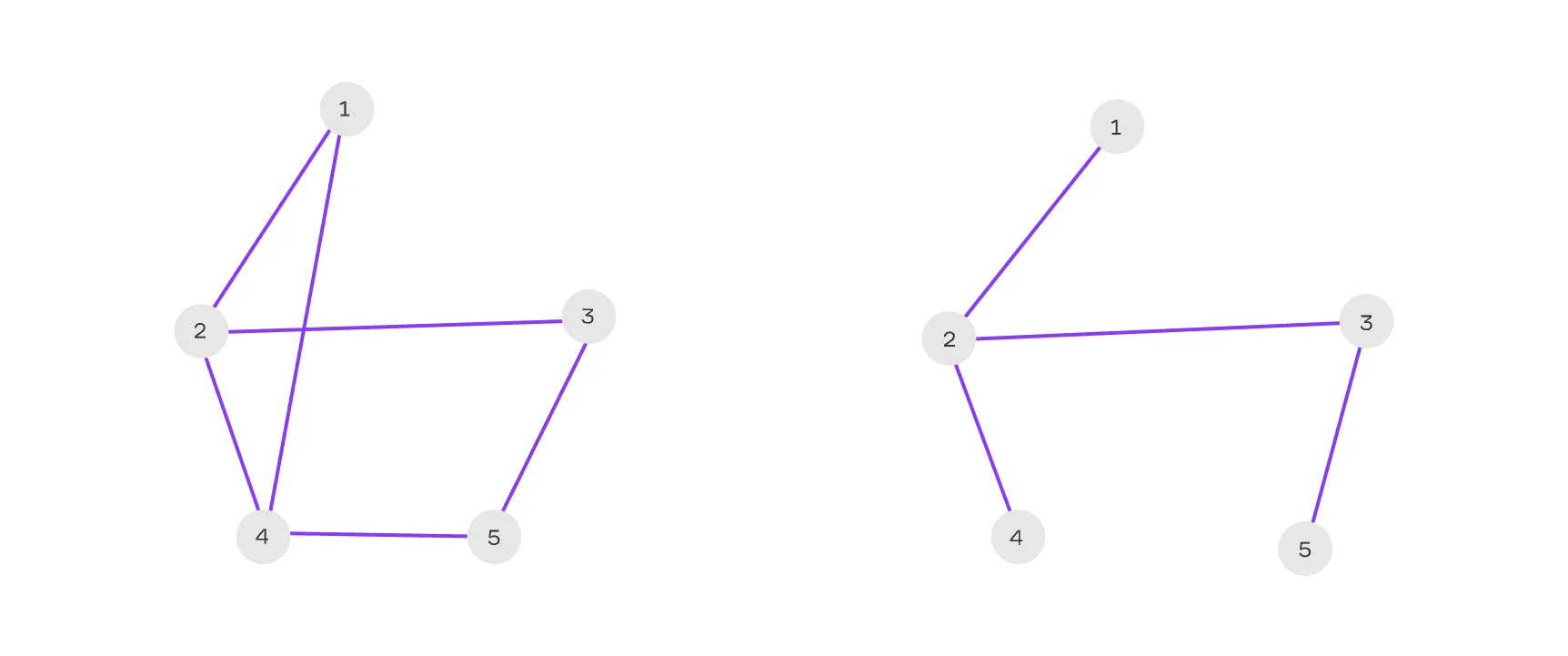
Остовное дерево — это подграф связного графа, который содержит все его вершины и также представляет собой дерево.

Можно представить остовное дерево как минимальный набор дорог, соединяющих все города страны без образования круговых маршрутов. Это важно в задачах оптимизации, где нужно минимизировать стоимость или длину связей.

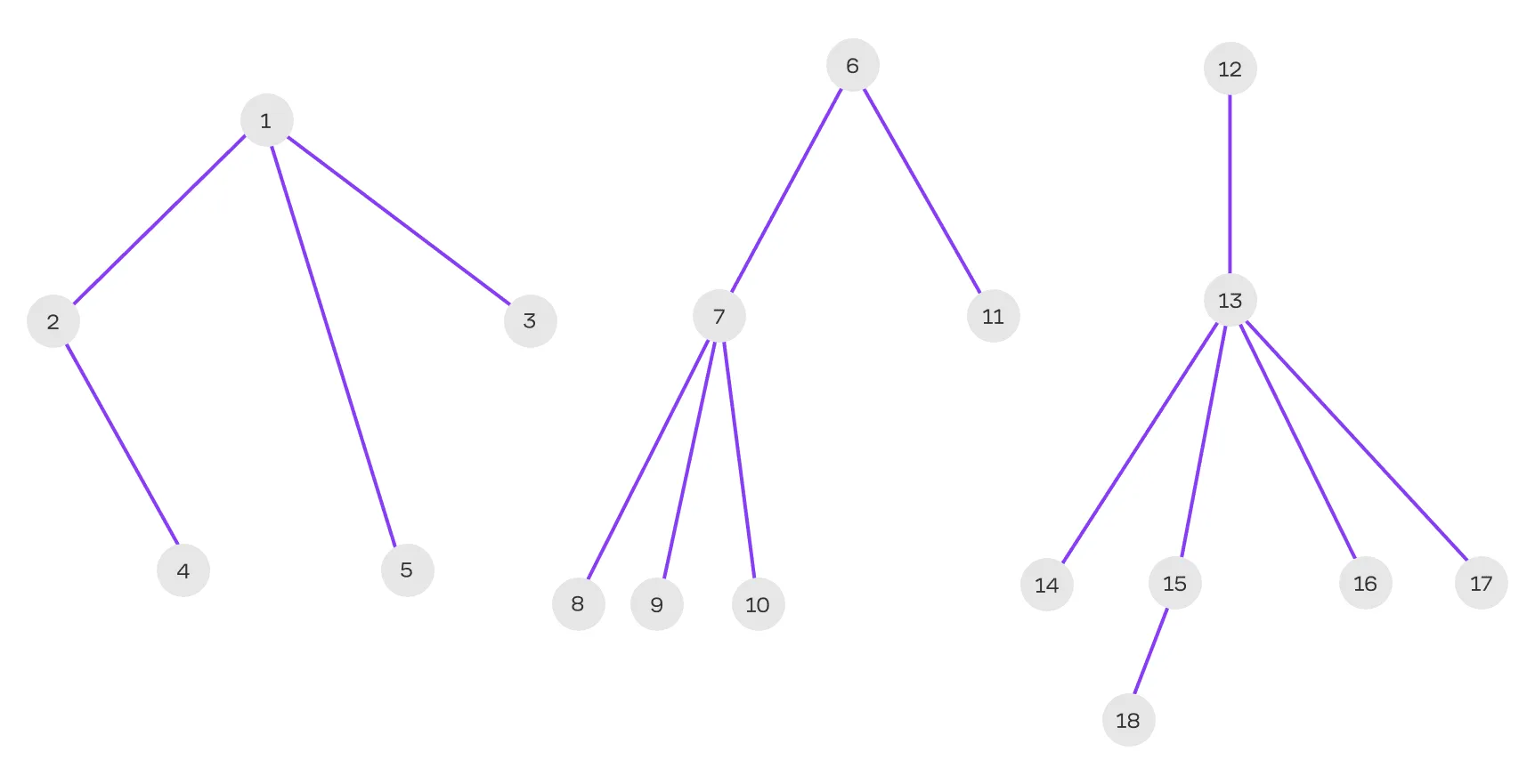
Если мы возьмём несколько деревьев и поместим их вместе без соединения между ними, мы получим лес.

В терминологии графов это несвязный неориентированный граф без циклов, состоящий из нескольких компонент, каждая из которых является деревом. Как множество отдельных островов с собственными деревьями, не связанных между собой.

С типами разобрались, давайте теперь рассмотрим ключевые теоремы о деревьях.

Теоремы о деревьях

Деревья обладают рядом уникальных свойств, которые делают их удобными для анализа и практических задач:

1. В любом дереве с двумя и более вершинами есть хотя бы одна висячая вершина (лист, вершина степени 1).
2. В дереве число вершин всегда на единицу больше, чем число рёбер.
3. У любого связного графа существует остовное дерево

Это важно: свойство №1 лежит в основе многих алгоритмов обработки деревьев. Свойство №2 помогает интуитивно понять структуру деревьев. А свойство №3 помогает оптимизировать графы.

И вот как можно формализовать и доказать эти свойства.

Теорема №1: висячая вершина в дереве

У нас есть утверждение: в дереве с более чем одной вершиной всегда существует хотя бы одна висячая вершина (лист).

Попробуем доказать его. Представьте, что вы гуляете по лабиринту без циклов (нашему дереву). Начав с любой вершины, вы можете идти по рёбрам, не возвращаясь назад. Поскольку дерево конечно, вы в итоге достигнете точки, из которой нет выхода, — это и будет висячая вершина.

Теорема №2: соотношение между вершинами и рёбрами

Утверждение следующее: в дереве число вершин на единицу больше, чем число рёбер, то есть , где — число вершин, — число рёбер.

Доказательство по индукции:

• База индукции: Для дерева с одной вершиной нет рёбер и соотношение выполняется.
• Шаг индукции: Предположим, что теорема верна для всех деревьев с вершиной. Возьмём дерево с вершинами. По теореме 1, у него есть висячая вершина. Удалим эту вершину и её единственное ребро. Оставшееся — дерево с вершиной и рёбрами, для которого, по предположению, верно . Возвращаясь к исходному дереву, получаем .

Это как строить цепочку из звеньев: каждое новое звено (вершина) добавляет одну связь (ребро), сохраняя целостность цепочки без замкнутых колец.

Теорема №3: остовное дерево связного графа

Мы утверждаем, у любого связного графа существует остовное дерево.

Рассмотрим связный граф, который можно представить как структуру со множеством узлов и циклов. Наша задача — удалить из графа избыточные рёбра, сохраняя связность и избегая образования циклов.

1. Начинаем с исходного связного графа.
2. Пока присутствуют циклы, удаляем по одному ребру из каждого из них. Это сохраняет связность, но устраняет замкнутость.
3. В результате получаем граф без циклов, который остаётся связным, — остовное дерево.

Мы рассмотрели основные свойства и теоремы, которые формализуют фундаментальные характеристики деревьев, подчёркивая их простоту и эффективность. Однако на практике связи между объектами редко бывают равнозначными: они часто сопровождаются дополнительной информацией — некоторыми весами.

Именно здесь на первый план выходят взвешенные деревья, позволяющие учитывать эти особенности и решать задачи оптимизации, где важна не только структура, но и её параметры.

Взвешенные деревья

В реальном мире связи между объектами часто имеют вес: расстояние между городами, стоимость перелётов, время передачи данных. Взвешенное дерево учитывает эти веса, что позволяет решать задачи оптимизации. Вес ребра может представлять различные величины, например:

• Расстояние. В транспортной сети вес ребра может представлять расстояние между двумя городами.
• Время. В сети передачи данных вес ребра может представлять время, необходимое для передачи данных между двумя узлами.
• Стоимость. В сети поставок вес ребра может представлять стоимость перевозки груза между двумя складами

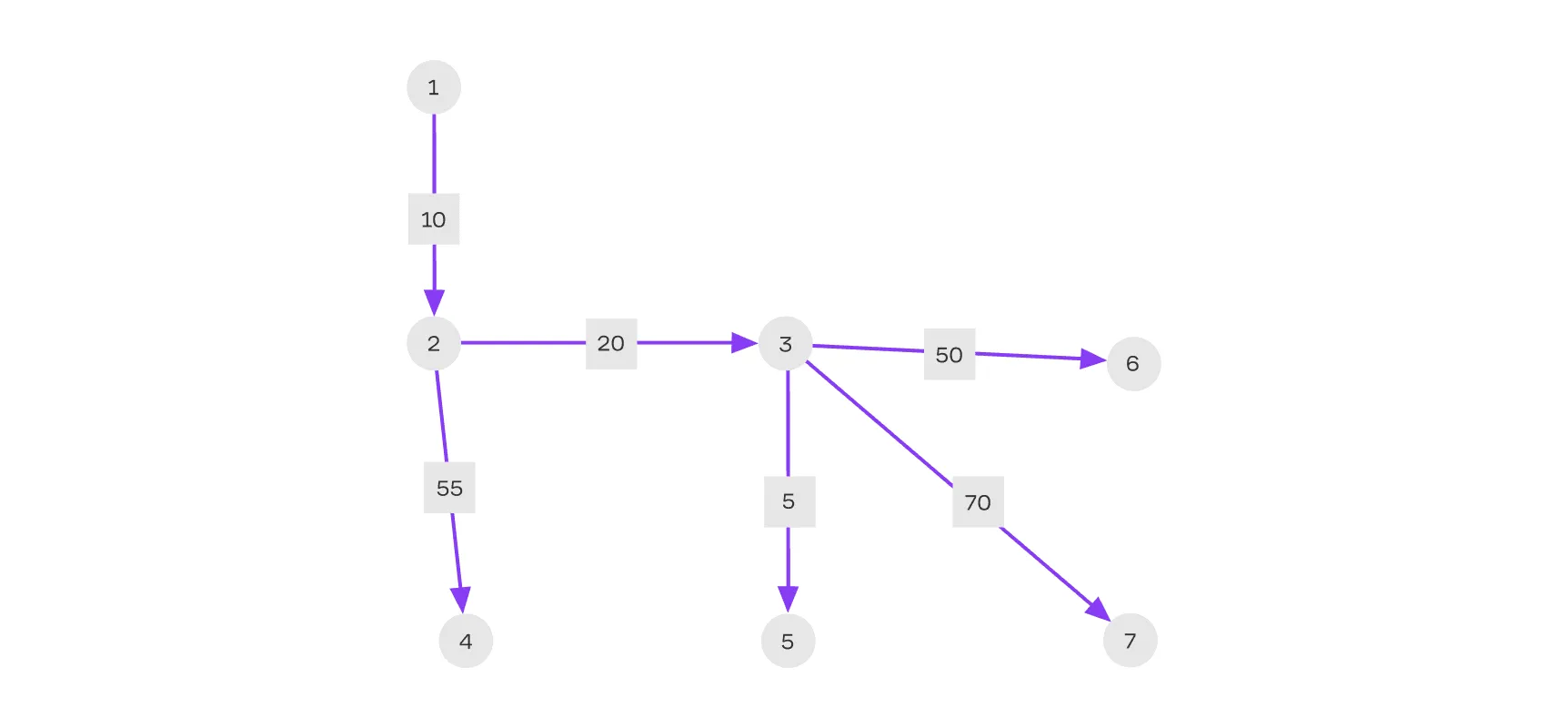
Для поиска оптимальных путей во взвешенных деревьях есть специальные алгоритмы. Рассмотрим их подробнее.

Алгоритм Дейкстры

Суть:

Это оптимальный выбор для нахождения кратчайших путей от начальной вершины к остальным, если все веса рёбер неотрицательные. Его логарифмическая сложность делает его подходящим для больших графов при условии, что отсутствуют отрицательные веса.

Принцип работы:

Представьте, что вы путешественник в незнакомом городе и хотите посетить все достопримечательности с минимальными затратами времени.

1. Инициализация:
   • Устанавливаем начальную вершину с нулевым расстоянием.
   • Остальные вершины получают бесконечное расстояние.
   • Все вершины считаются необработанными.
2. Шаги алгоритма:
   • Выбираем необработанную вершину с наименьшим текущим расстоянием до неё.
   • Для каждого соседа текущей вершины:
     • Вес ребра между текущей вершиной и соседом — это заданная величина, характеризующая связь между ними.
     • Вычисляем новое потенциальное расстояние до соседа: сумма текущего расстояния до вершины и веса ребра между ними.
     • Если это расстояние меньше ранее известного расстояния до соседа, обновляем его.
   • Помечаем текущую вершину как обработанную.
3. Завершение:
   • Процесс повторяется, пока все вершины не будут обработаны.

Преимущества и ограничения:

• Плюсы: эффективен и гарантирует оптимальные решения для графов с неотрицательными весами.
• Минусы: не работает с отрицательными весами рёбер.

1import heapq
2
3def dijkstra(graph, start):
4    distance = {vertex: float('inf') for vertex in graph}
5    distance[start] = 0
6    priority_queue = [(0, start)]  # (расстояние, вершина)
7
8    while priority_queue:
9        current_distance, current_vertex = heapq.heappop(priority_queue)
10
11        # Если найден более короткий путь, пропускаем
12        if current_distance > distance[current_vertex]:
13            continue
14
15        for neighbor, weight in graph[current_vertex]:
16            distance_to_neighbor = current_distance + weight
17
18            if distance_to_neighbor < distance[neighbor]:
19                distance[neighbor] = distance_to_neighbor
20                heapq.heappush(priority_queue, (distance_to_neighbor, neighbor))
21
22    return distance
23
24# Пример использования
25graph = {
26    'A': [('B', 1), ('C', 4)],
27    'B': [('C', 2), ('D', 5)],
28    'C': [('D', 1)],
29    'D': []
30}
31
32distances = dijkstra(graph, 'A')
33print(distances)  # {'A': 0, 'B': 1, 'C': 3, 'D': 4}

Алгоритм Беллмана — Форда

Суть:

Позволяет находить кратчайшие пути от заданной вершины до всех остальных, даже если в графе присутствуют отрицательные веса рёбер. Однако алгоритм лучше применять для средних по размеру графов, поскольку его временная сложность составляет , где:

• — количество вершин в графе,
• — количество рёбер в графе.

Принцип работы:

Алгоритм последовательно релаксирует (обновляет) расстояния, проходя по всем рёбрам многократно.

1. Инициализация:
   • Как в алгоритме Дейкстры.
2. Шаги алгоритма:
   • Повторяем процесс релаксации ребер раз, где — количество вершин.
   • Проверяем на наличие отрицательных циклов.

Преимущества и ограничения:

• Плюсы: работает с отрицательными весами.
• Минусы: более медленный, сложность .

1def bellman_ford(graph, source):
2    distance = {vertex: float('inf') for vertex in graph}
3    distance[source] = 0
4
5    for _ in range(len(graph) - 1):
6        for vertex in graph:
7            for neighbor, weight in graph[vertex]:
8                if distance[vertex] + weight < distance[neighbor]:
9                    distance[neighbor] = distance[vertex] + weight
10
11    # Проверка на отрицательные циклы
12    for vertex in graph:
13        for neighbor, weight in graph[vertex]:
14            if distance[vertex] + weight < distance[neighbor]:
15                raise ValueError("Граф содержит отрицательный цикл")
16
17    return distance
18
19# Пример использования
20graph = {
21    'A': [('B', 4), ('C', 2)],
22    'B': [('C', -1), ('D', 2)],
23    'C': [('D', 3)],
24    'D': []
25}
26
27distances = bellman_ford(graph, 'A')
28print(distances)  # {'A': 0, 'B': 4, 'C': 2, 'D': 5}

Алгоритм Флойда — Уоршелла

Суть:

Подходит для поиска кратчайших путей между всеми парами вершин. Он работает на основе матрицы расстояний, которая представляет собой квадратную таблицу, где элемент на пересечении строки и столбца показывает текущее минимальное расстояние от вершины
до вершины . Постепенно обновляя значения в этой таблице, алгоритм находит минимальные пути между всеми парами вершин.

При этом алгоритм способен обрабатывать графы с отрицательными весами рёбер, хотя его сложность делает его менее эффективным для очень больших сетей.

Принцип работы:

Представьте, что вы хотите узнать минимальные расстояния между всеми парами городов в стране.

1. Инициализация:
   • Создаём матрицу расстояний между всеми вершинами.
2. Шаги алгоритма:
   • Постепенно улучшаем оценки расстояний, рассматривая все возможные промежуточные вершины.

Преимущества и ограничения:

• Плюсы: работает с отрицательными весами рёбер и прост в реализации.
• Минусы: сложность делает алгоритм медленным для больших графов.

1import numpy as np
2
3def floyd_warshall(graph):
4    num_vertices = len(graph)
5    dist = np.array(graph)
6
7    for k in range(num_vertices):
8        for i in range(num_vertices):
9            for j in range(num_vertices):
10                if dist[i][k] + dist[k][j] < dist[i][j]:
11                    dist[i][j] = dist[i][k] + dist[k][j]
12
13    return dist
14
15# Пример использования
16graph = [
17    [0, 3, float('inf'), 5],
18    [2, 0, float('inf'), 4],
19    [float('inf'), 1, 0, float('inf')],
20    [float('inf'), float('inf'), 2, 0]
21]
22
23shortest_paths = floyd_warshall(graph)
24print(shortest_paths)

Теория графов и, в частности, деревья — это мощный инструмент для моделирования и решения разнообразных задач. Понимая, как элементы связаны между собой, мы можем принимать более обоснованные решения и находить эффективные пути решения проблем.

Если вы хотите углубить свои знания и применить их на практике, с алгоритмическими заданиями по графам вы можете ознакомиться в хендбуке по алгоритмическому программированию.

В нём рассматриваются такие важные темы, как поиск в ширину (BFS), поиск в глубину (DFS), обходы графа, алгоритм нахождения компонент связности в графе и многое другое. Это поможет вам освоить ключевые алгоритмы и применить теоретические знания на практике, делая ваши решения ещё более эффективными и продуманными.

А сейчас перейдём к квизам и задачам на закрепление материала.