Дифференцирование — это один из ключевых инструментов математического анализа, который позволяет исследовать, как функция изменяется в каждой точке. Это понятие лежит в основе многих процессов в анализе данных и машинном обучении: от оптимизации функций потерь до вычисления градиентов и анализа поведения сложных моделей.
В этом параграфе мы подробно разберём:
- Производную и правила дифференцирования, чтобы понять, как находить скорость изменения функции и применять основные правила для работы со сложными выражениями.
- Теоремы Ролля и Лагранжа, которые дадут представление о том, как экстремумы (точки максимума и минимума функций) и изменения функции связаны с её производной.
- Применение производной на практике, где на конкретных примерах посмотрим, как использовать дифференцирование для нахождения экстремумов и анализа моделей.
Вы познакомитесь с основами, которые не только расширят понимание теории, но и помогут разобраться, как применять эти методы в задачах оптимизации и анализа данных.
А начнём мы с понятия производной и основных правил дифференцирования, которые служат фундаментом для дальнейших разделов.
Производная и правила дифференцирования
Когда мы изучаем поведение функции, нам важно не только знать значения самой функции в различных точках, но и понимать, как они меняются. Производная — это ключевой инструмент, который позволяет количественно описать скорость изменения функции в точке. Она описывает, насколько быстро изменяется значение функции , когда её аргумент изменяется на бесконечно малую величину.
Формальное определение
Производная функции в точке определяется как предел отношения приращения функции к приращению аргумента, если этот предел существует:
Где:
- — малое изменение (приращение) аргумента функции,
- — соответствующее изменение (приращение) значения функции.
Функция называется дифференцируемой в точке , если её производная существует. Это означает, что предел, представленный в формальном определении, существует и конечен.
Если функция дифференцируема в каждой точке некоторого интервала, она называется дифференцируемой на этом интервале.
Важно отметить, что если функция дифференцируема в точке , то она обязательно непрерывна в этой точке. Однако обратное не всегда верно: непрерывность функции не гарантирует её дифференцируемость. Например, функция непрерывна во всех точках, но не дифференцируема в точке .
О различных формах нотации производной
Для обозначения производной существуют разные нотации, каждая из которых находит применение в зависимости от ситуации и удобства. Давайте рассмотрим основные из них.
-
Лагранжева нотация:
Эта нотация наиболее часто используется в классическом математическом анализе и кратко указывает на производную функции или по её аргументу .
- Пример: — производная функции в точке .
-
Нотация Лейбница:
Эта нотация подчёркивает изменения зависимой переменной относительно независимой переменной . Она особенно удобна в приложениях, таких как физика, где важно различать изменение переменных.
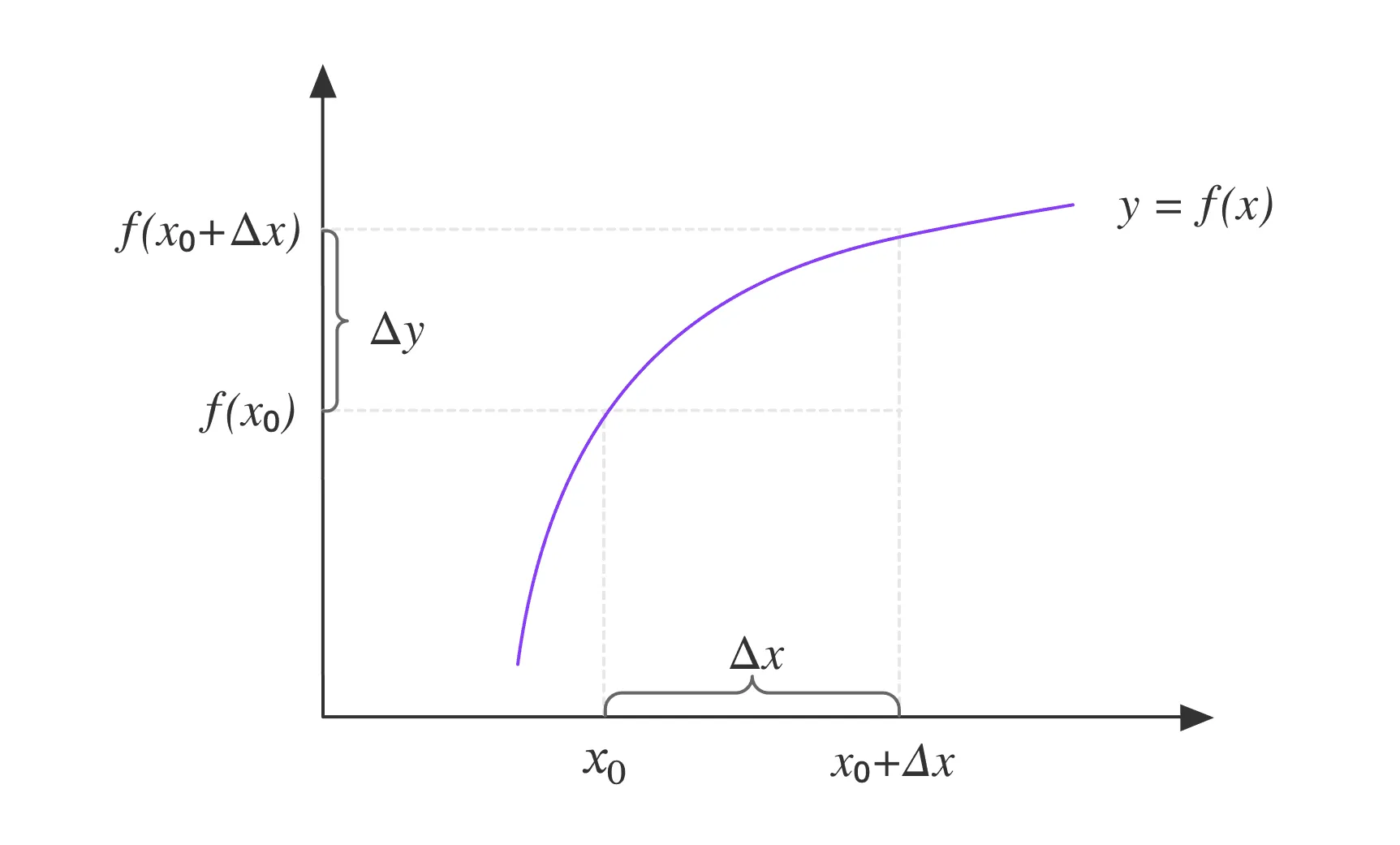
- Пример: читается как «изменение относительно изменения ».
-
Ньютонианская нотация:
Эта форма используется в основном для производных по времени, например в механике. Первая производная обозначается одной точкой над функцией, а вторая — двумя. Такая нотация полезна, например, в задачах динамики.
- Пример: — скорость, — ускорение.
-
Операторная нотация:
Здесь используется для обозначения дифференцирования. Такой формат удобен для работы с более сложными операторами, особенно в многомерных задачах.
- Пример: обозначает вторую производную функции .
В каждой нотации скрыта идея предела:
Все эти формы отражают одно и то же: стремление к локальному описанию изменений функции. Каждое из них подходит для определённого контекста: от глубокого теоретического анализа до прикладных задач в вычислениях и программировании. Важно помнить, что, независимо от выбранной нотации, суть операции остаётся неизменной.
Теперь попробуем понять геометрический смысл производной через такие понятия, как секущая линия и касательная.
Секущая линия — это прямая, которая пересекает график функции в двух точках. Если эти две точки всё ближе смещаются друг к другу, секущая линия начинает «приближаться» к касательной — прямой, которая касается графика функции только в одной точке и имеет с ним одинаковый наклон.
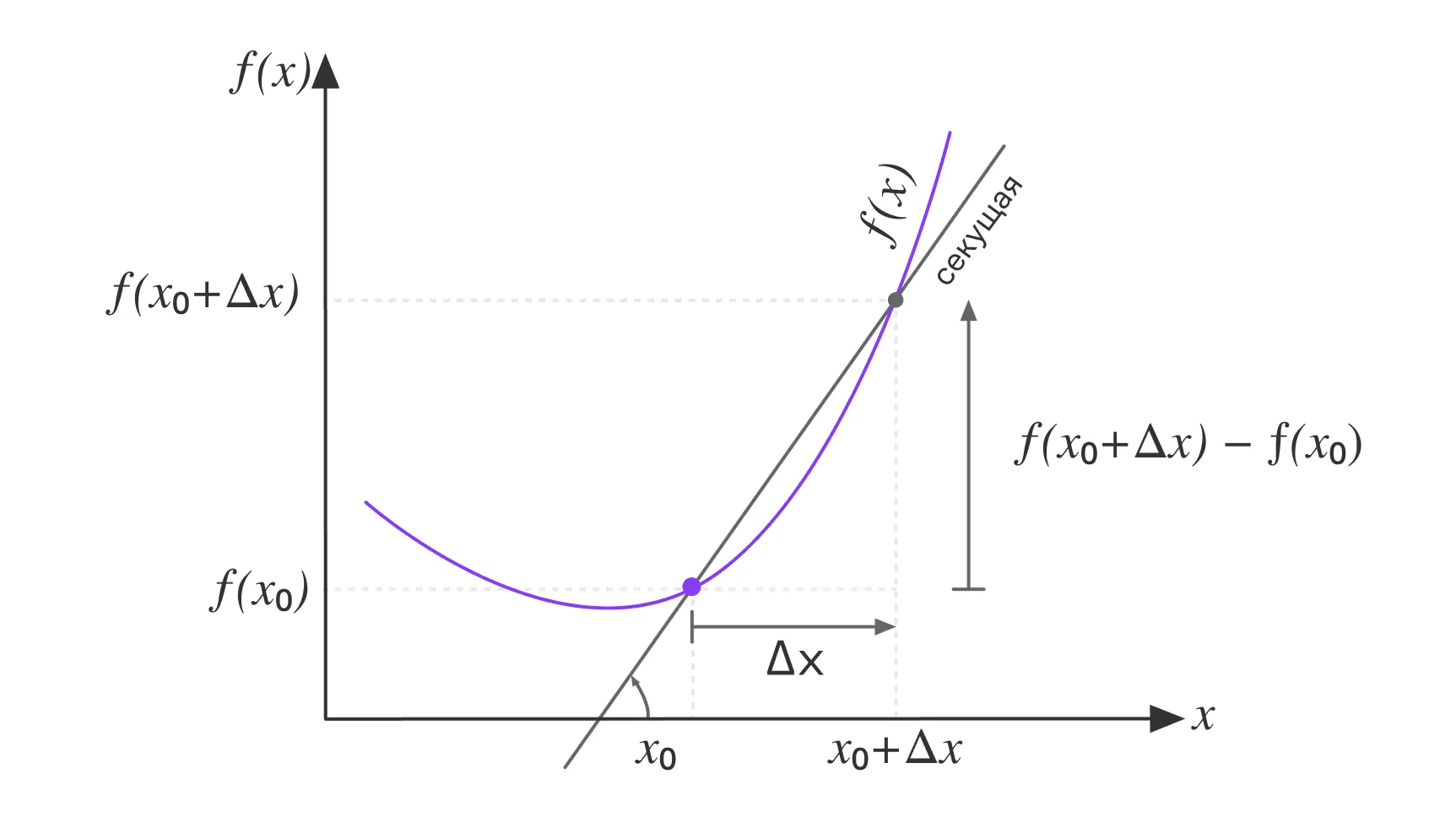
На иллюстрации мы видим, как формула производной основывается на секущей линии, наклон которой определяется отношением приращений и :
Здесь — расстояние между точками по горизонтали, а это изменение функции между этими точками. Это отношение даёт наклон секущей, который описывает среднюю скорость изменения функции на интервале . Однако это ещё не производная.
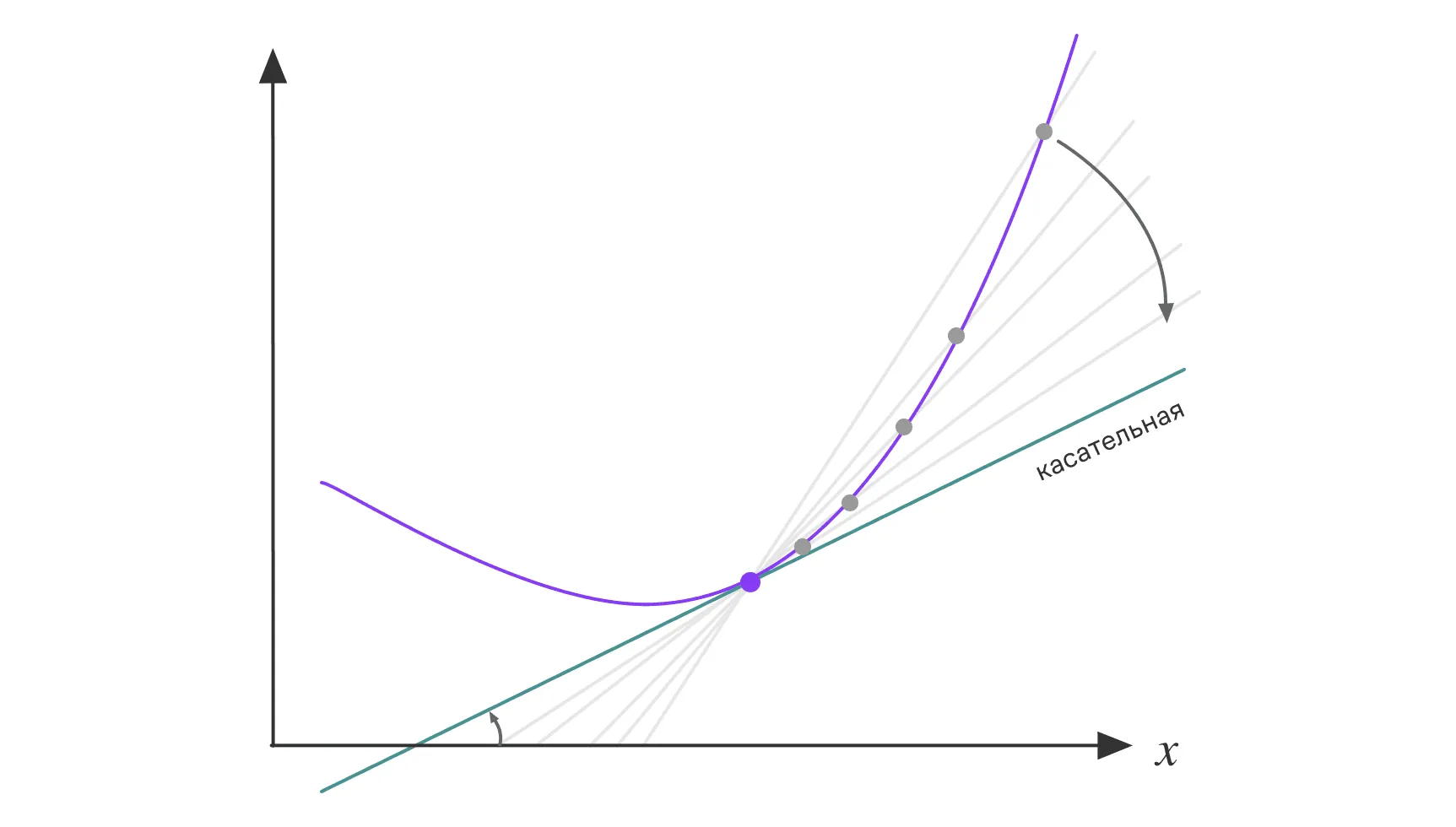
Производная появляется, когда мы «приближаем» точку пересечения секущей с графиком к одной-единственной точке с координатами , то есть берём предел при . В этом случае секущая линия становится касательной, а её наклон — это уже точная скорость изменения функции в точке:
В реальных вычислениях (например, в численных методах) мы часто не можем работать с идеальными математическими пределами. Вместо этого мы используем приближения:
- Если у нас есть только конечные данные (например, измеренные точки функции), мы можем построить секущую линию между двумя соседними точками и оценить производную.
- Это приближение особенно важно для численного дифференцирования в таких областях, как обработка сигналов, оптимизация и машинное обучение.
Пример вычисления производной
Рассмотрим функцию . Найдем её производную в точке :
Раскроем скобки:
Сокращаем на :
При :
В точке :
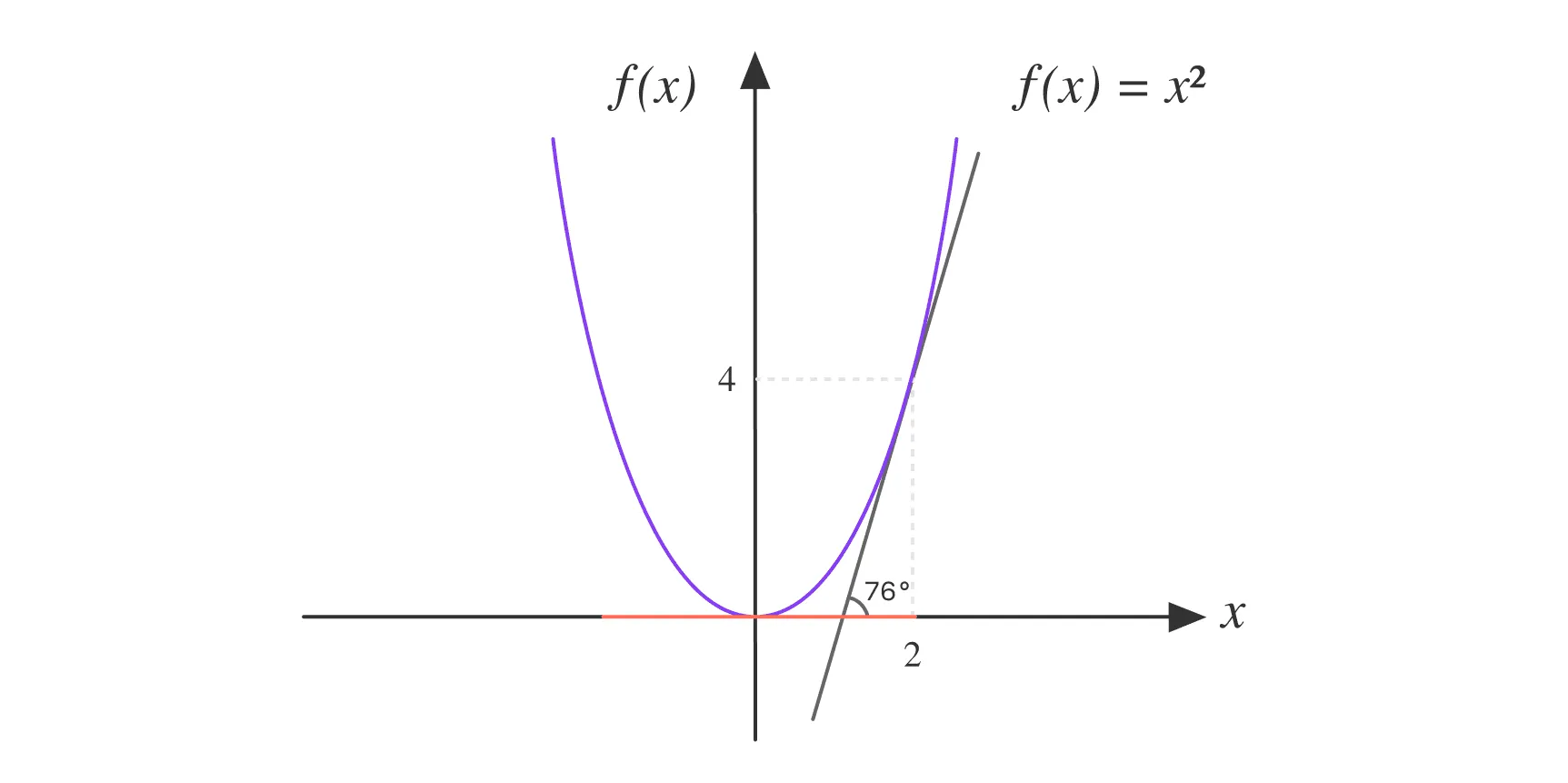
Важно: В примере выше мы использовали формальное определение производной через предел, чтобы показать весь процесс вычисления «с нуля». Однако в большинстве случаев такой подход оказывается избыточно громоздким.
В повседневной работе часто используются заранее известные производные для наиболее распространённых функций, таких как степенные, экспоненциальные, логарифмические и тригонометрические. Эти производные составляют основу, на которой строится работа с более сложными выражениями.
Давайте рассмотрим производные основных функций, прежде чем перейти к правилам дифференцирования.
Производные основных функций
Для дальнейшей работы с производными важно знать производные наиболее часто встречающихся функций. Ниже приведены основные из них:
- Степенная функция: .
- Экспоненциальная функция: .
- Логарифм: .
- Синус и косинус: , .
Полную таблицу с основными функциями и их производными можно найти в справочной таблице ниже.
Справочная таблица по производным основных функций

Примечания:
- Сложные функции. Для функций, которые представляют собой комбинации основных, можно применять правила дифференцирования, такие как правило суммы, произведения, частного и цепное правило.
- Периодические ограничения. Для тригонометрических функций производные имеют ограничения в точках разрывов (например, разрывна в ).
Освоив их, вы сможете быстро находить производные сложных функций, комбинируя правила дифференцирования, которые мы рассмотрим далее.
Правила дифференцирования
Чтобы вычислять производные сложных функций, используются специальные правила, которые упрощают процесс.
- Производная суммы или разности:
Если и — дифференцируемые функции, то:
Пример: Пусть . Тогда: .
- Производная произведения (правило Лейбница):
Если и — дифференцируемые функции, то:
Пример: Пусть . Тогда:
- Производная частного:
Если и — дифференцируемые функции, и , то:
Пример: Пусть . Тогда:
- Производная сложной функции (правило цепочки):
Если и , то:
Пример: Пусть . Тогда:
Итак, с производными разобрались. Теперь самое время поговорить о том, как изменение функции на некотором интервале связано со значениями её производных внутри этого интервала.
В этом нам помогут теоремы Ролля и Лагранжа, которые играют ключевую роль в анализе поведения функций и предоставляют теоретическую основу для многих методов оптимизации и решения прикладных задач.
Теоремы Ролля и Лагранжа
В дифференциальном исчислении существуют фундаментальные теоремы, которые связывают поведение функции на отрезке с поведением её производных. Две из таких теорем — теорема Ролля и теорема Лагранжа (также известная как теорема о среднем значении). Они дают теоретическую основу для многих методов оптимизации и решения прикладных задач, например анализа изменений функции потерь в обучении моделей машинного обучения.
Теорема Ролля
Сначала посмотрим на формулировку теоремы Ролля, а затем на её интуитивное понимание:
Пусть функция удовлетворяет следующим условиям на отрезке :
- Непрерывность на отрезке . Функция непрерывна на всём отрезке от до .
- Дифференцируемость на интервале . Функция имеет производную в каждой точке внутри интервала .
- Равенство значений на концах отрезка: .
Тогда существует хотя бы одна точка в интервале такая, что:
Теорема Ролля говорит нам, что если функция начинается и заканчивается на одной и той же высоте (т. е. ) и она непрерывна и дифференцируема внутри отрезка, то где-то между и функция должна иметь горизонтальную касательную, то есть производная должна быть нулевой. Это похоже на то, как если бы вы шли по холму и вернулись в ту же самую точку по высоте — где-то вы должны были либо подниматься, либо спускаться, а в какой-то момент идти по горизонтали.
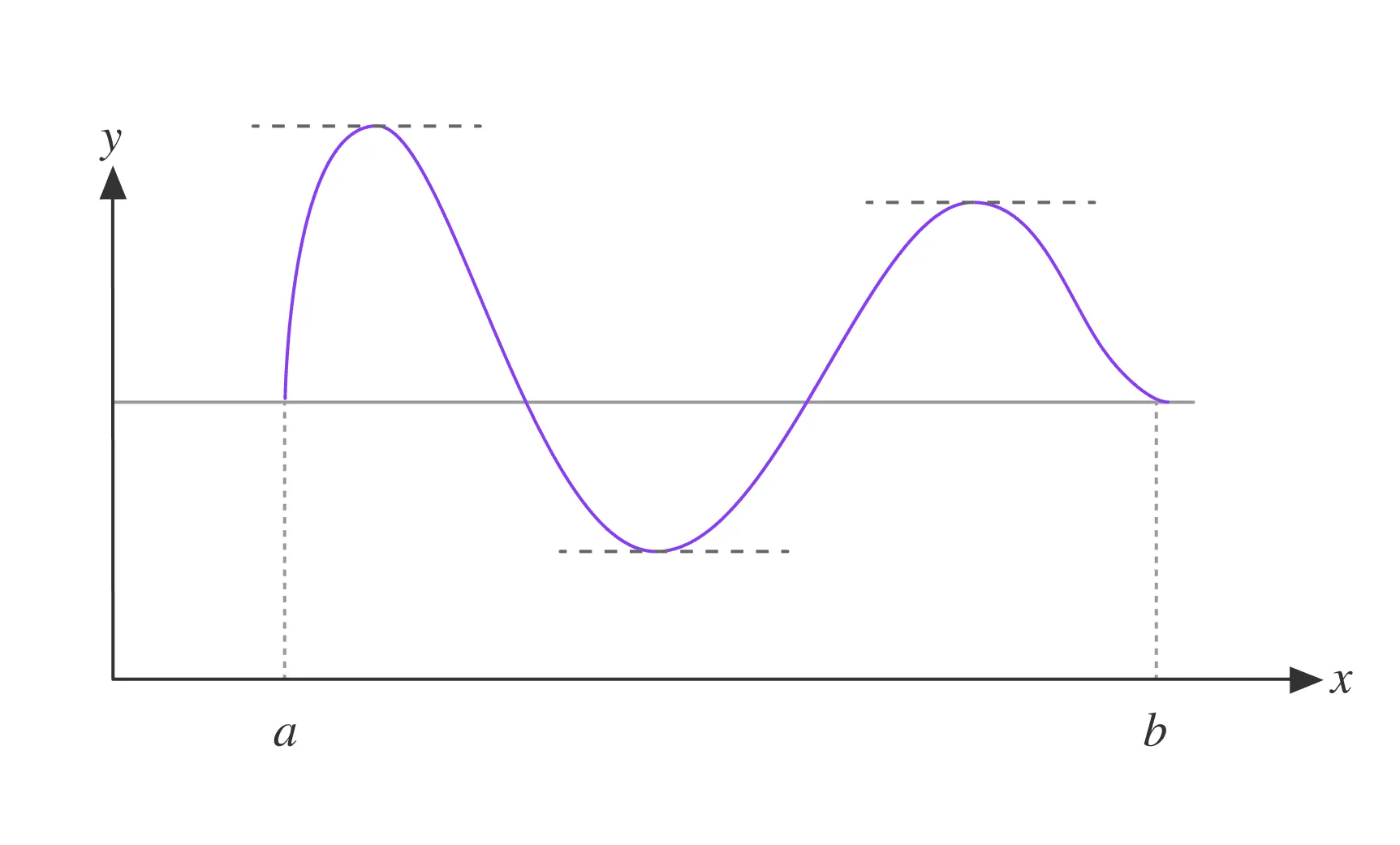
Пример
Рассмотрим функцию на отрезке :
- Непрерывность. Функция непрерывна на всём множестве действительных чисел, в частности на .
- Дифференцируемость. Производная существует для всех , значит, функция дифференцируема на .
- Равенство значений на концах отрезка. и .
По теореме Ролля, существует точка , такая что . Найдём эту точку:
Таким образом, в точке производная функции равна нулю.
Если совсем упростить значимость теоремы Ролля, то она гарантирует наличие экстремума (минимума или максимума) при определённых условиях. Получается, что в задачах минимизации или максимизации функций (например, в машинном обучении при оптимизации функции потерь) именно эта теорема помогает установить условия существования экстремумов.
Прикладной пример
Рассмотрим задачу прогнозирования сезонных продаж, где требуется определить, в какой момент продажи достигли локального пика (максимума) или дна (минимума) за месяц. Пусть значения продаж заданы как функция , где — дни месяца. Предположим, что продажи в первый и последний день месяца совпадают, т. е. .
Применяя теорему Ролля, можем утверждать, что существует хотя бы один день , в который производная равна нулю, т. е. продажи не меняются (локальный пик или дно). Этот результат может быть использован для анализа трендов и определения наиболее значимых дней в месяце, когда изменения в продажах могут повлиять на стратегию.
Возьмём , где :
- Непрерывность: непрерывна на .
- Дифференцируемость: существует на .
- Равенство значений на концах отрезка:
По теореме Ролля, существует точка , где . Найдём эту точку, решив уравнение:
Решение:
На интервале единственным решением является: , что соответствует середине между 15-м и 16-м днями месяца.
Таким образом, продажи достигают локального максимума или минимума вблизи 15-го и 16-го дней месяца. Этот результат можно использовать для прогнозирования сезонных изменений продаж или планирования акций, определяя ключевые периоды, когда изменения в продажах наиболее значимы.
Теорема Лагранжа
Взглянем на формулировку теоремы:
Пусть функция удовлетворяет следующим условиям на отрезке :
- Непрерывность на отрезке . Функция непрерывна на всём отрезке от до .
- Дифференцируемость на интервале . Функция имеет производную в каждой точке внутри интервала .
Тогда существует хотя бы одна точка в интервале такая, что:
Теорема Лагранжа утверждает, что на интервале существует точка, в которой мгновенная скорость изменения функции (производная) равна средней скорости изменения функции на всём отрезке.
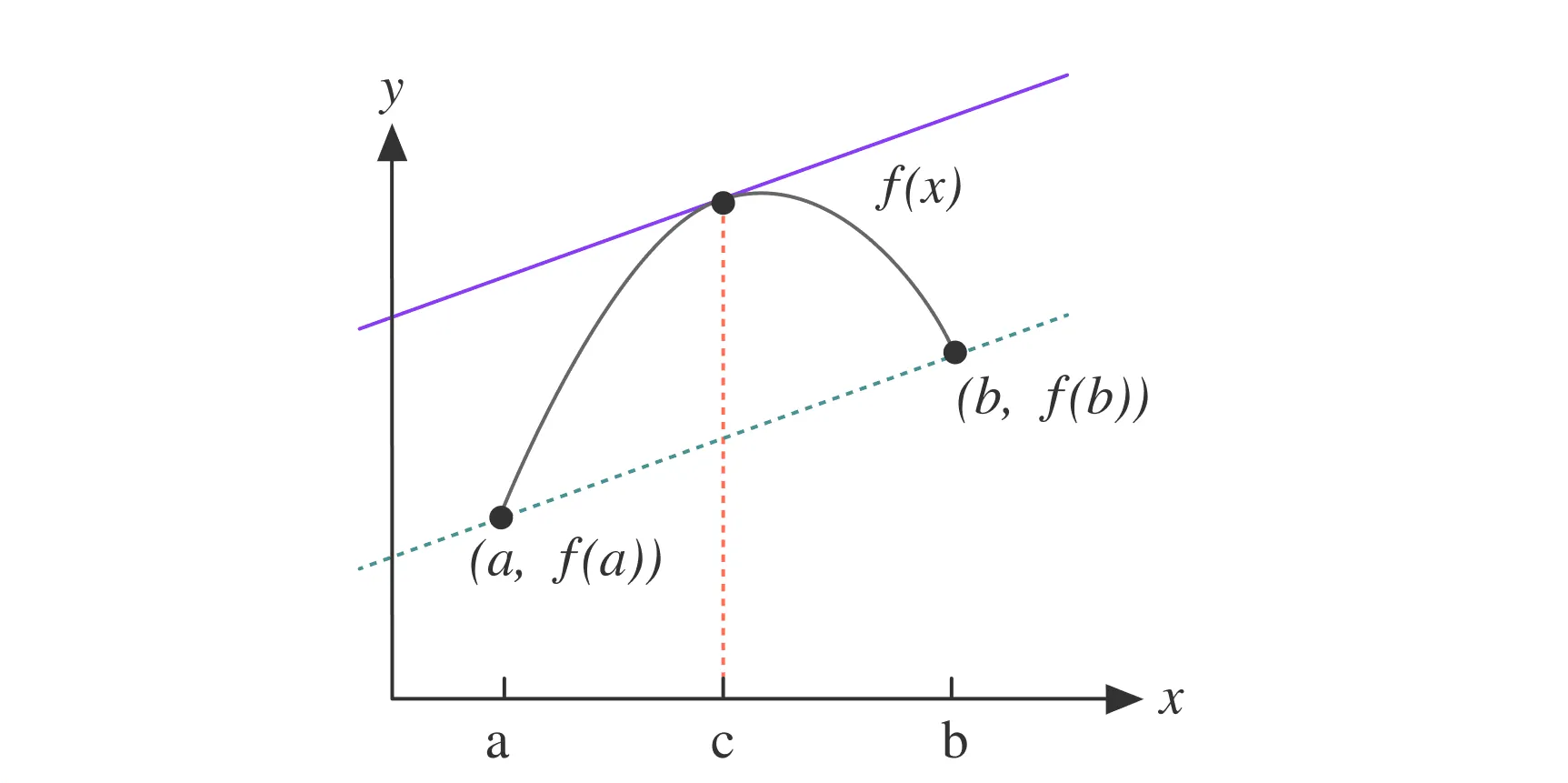
Это означает, что касательная к графику функции в точке параллельна секущей, которая соединяет точки и . В какой-то мере теорема обобщает утверждение теоремы Ролля и связывает среднее изменение функции с её производной.
Пример
В качестве примера рассмотрим функцию на отрезке :
- Непрерывность. Полиномиальные функции, такие как , непрерывны на всём множестве действительных чисел.
- Дифференцируемость. Производная существует для всех , значит, функция дифференцируема на .
Вычислим среднюю скорость изменения функции на отрезке :
По теореме Лагранжа, существует точка , такая, что:
Вычислим и решим уравнение:
Таким образом, в точке мгновенная скорость изменения функции равна средней скорости изменения на отрезке.
Теорема Лагранжа находит применение в оптимизации и анализе производительности функций, показывая, где скорость изменения функции соответствует средней. А также в контексте машинного обучения данная теорема помогает понять и доказать сходимость алгоритмов, поведение функций потерь и градиентов.
Прикладной пример
Предположим, мы обучаем модель линейной регрессии и используем функцию потерь , зависящую от параметра . Если непрерывна и дифференцируема на отрезке , то, по теореме Лагранжа, существует значение между и , такое, что:
Это значит, что изменение функции потерь между двумя значениями параметра можно связать с производной в некоторой точке между ними. Это полезно для анализа скорости сходимости алгоритмов оптимизации и выбора шагов изменения параметров.
Обе теоремы — мощные инструменты, которые помогают глубже понять поведение функций. Они связывают значение функции с её производной, предоставляя теоретическую основу для анализа изменения функций и задач оптимизации.
В следующей части мы применим эти результаты для оптимизации простых моделей.
Оптимизация простых моделей и анализ изменения функций
Давайте разберём основы оптимизации функций — процесса поиска экстремальных значений (минимумов и максимумов), которые играют важную роль в математическом анализе, физике, экономике и особенно в машинном обучении.
Мы посмотрим, как производные позволяют находить точки экстремумов и анализировать поведение функций на разных интервалах.
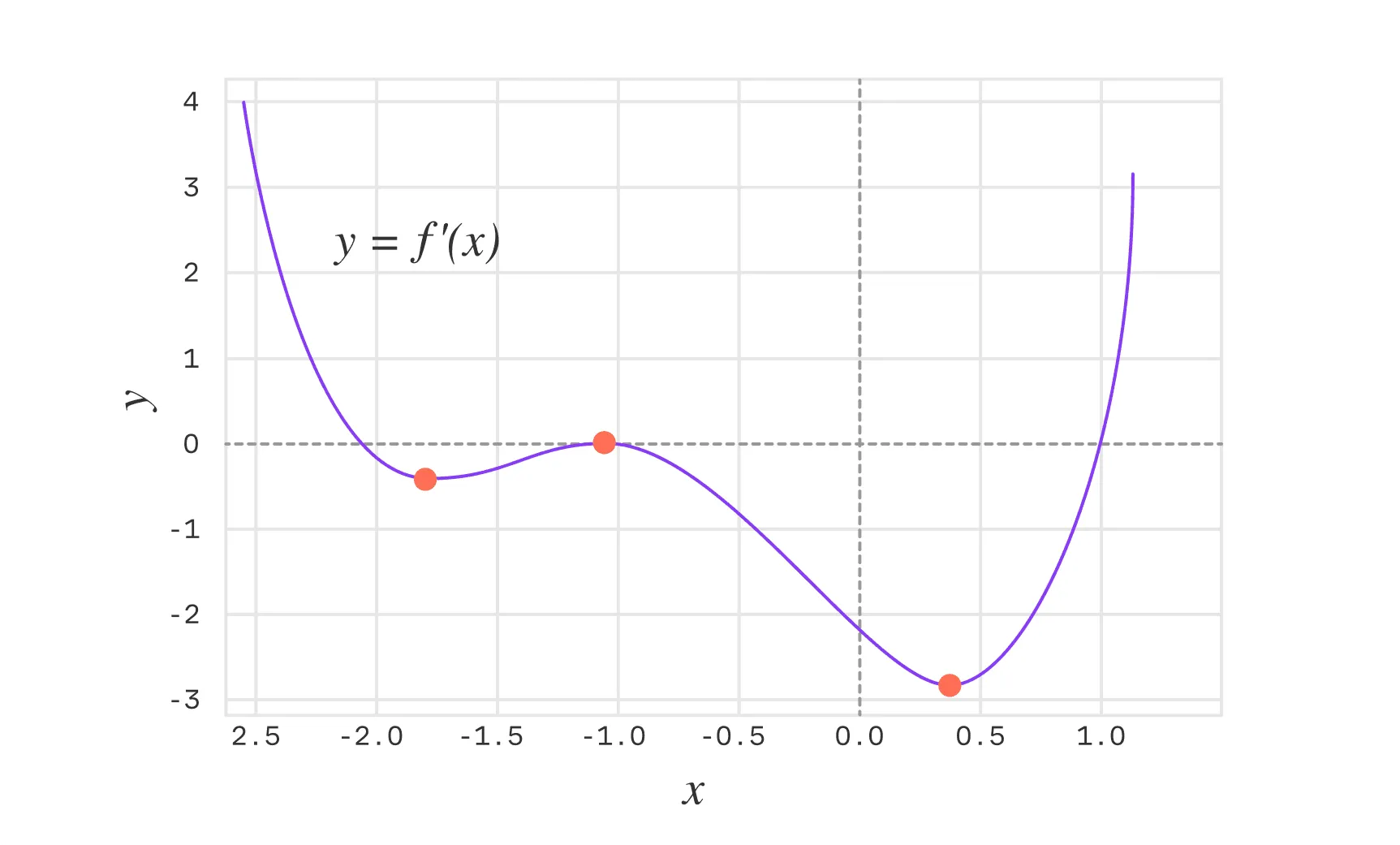
Критические точки функции
Оптимизация — это поиск таких значений, при которых функция принимает своё наименьшее или наибольшее значение. Например:
- В экономике задача может заключаться в максимизации прибыли.
- В машинном обучении — в минимизации функции потерь для настройки параметров модели.
Производные дают точный инструмент для решения этих задач, так как они описывают скорость изменения функции и позволяют выявить её критические точки — места, где функция перестаёт возрастать или убывать. В критических точках первая производная функции равна нулю или не существует. То есть такие точки — потенциальные кандидаты на искомые экстремумы.
Функция имеет экстремум в точке , если в этой точке она достигает локального минимума или максимума:
- Локальный минимум — значение функции меньше всех остальных значений в небольшой окрестности точки.
- Локальный максимум — значение функции больше всех остальных значений в небольшой окрестности точки.
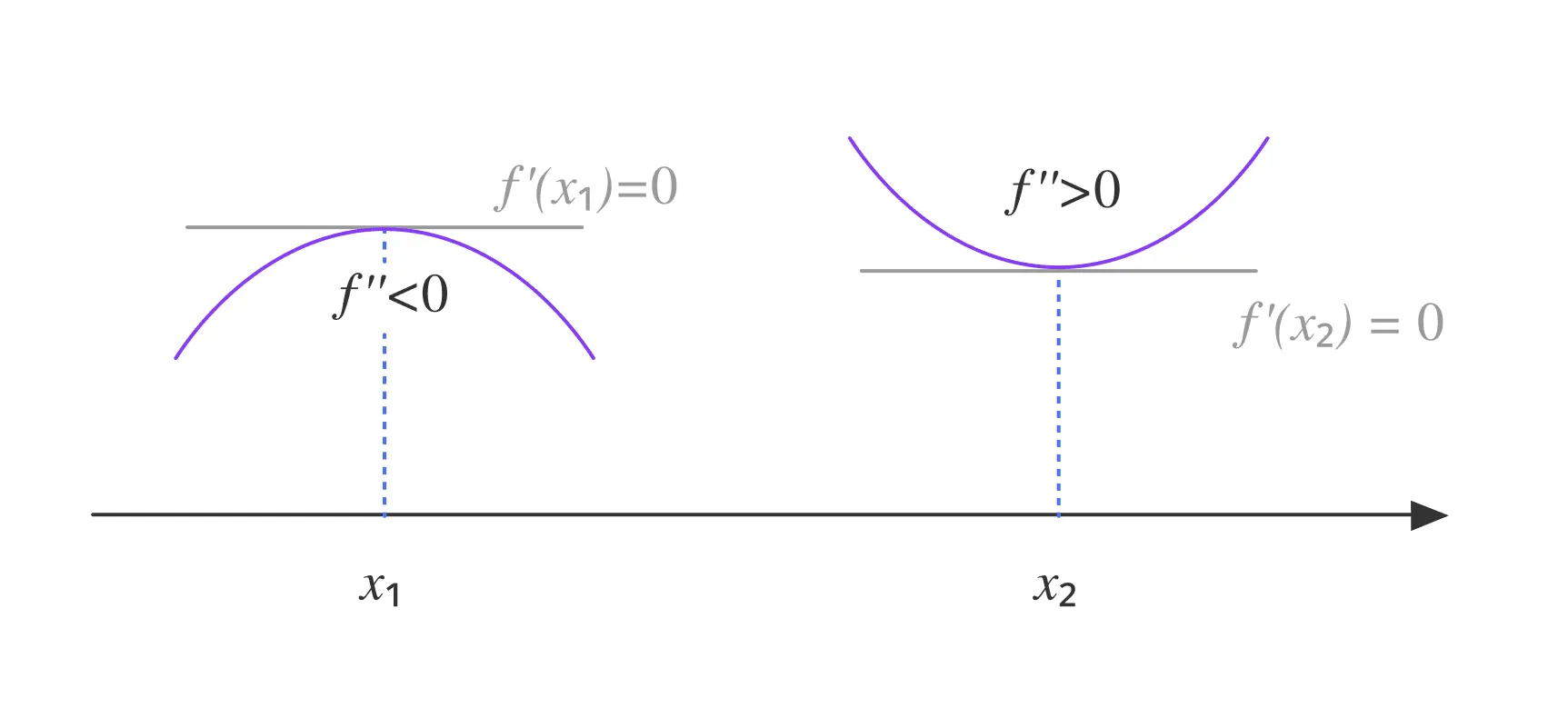
Важно отметить, что в точках экстремума , где функция дифференцируема, её первая производная равна нулю: . Однако не все критические точки являются экстремумами — это зависит от поведения функции в окрестности точки.
Для анализа характера этих точек (локальный минимум, максимум или перегиб) используется:
- Первая производная — для нахождения критических точек.
- Вторая производная — для определения выпуклости функции в этих точках.
Выпуклость функции — это свойство, описывающее, как функция изменяется на заданном интервале. Функция называется выпуклой вниз (или просто выпуклой), если её график «лежит ниже» любой прямой, соединяющей две произвольные точки на графике. Аналогично функция выпукла вверх (или вогнута), если её график «лежит выше» такой прямой.
Этапы оптимизации функций
- Нахождение критических точек:
- Вычисляем первую производную .
- Находим точки, где или не существует. Эти точки называются критическими.
- Анализ характера критических точек:
- С помощью второй производной :
- Если , в точке — локальный минимум.
- Если , в точке — локальный максимум.
- Если , требуется дополнительный анализ (например, исследование выпуклости функции).
- С помощью второй производной :
- Определение интервалов возрастания и убывания:
- Если на интервале, функция возрастает.
- Если , функция убывает.
- Анализ выпуклости функции:
- Если на интервале, функция выпукла вниз.
- Если , функция выпукла вверх.
- Оценка на границах:
- Если функция определена на отрезке , нужно также проверить её значения в точках , и критических точках.
Пример
Рассмотрим функцию . Найдём её экстремумы.
-
Находим первую производную: .
-
Решаем уравнение :
-
Находим вторую производную:
Следовательно, точка является локальным минимумом.
-
Вычисляем значение функции в этой точке:
-
Интервалы возрастания и убывания:
- для : функция возрастает.
- для : функция убывает.
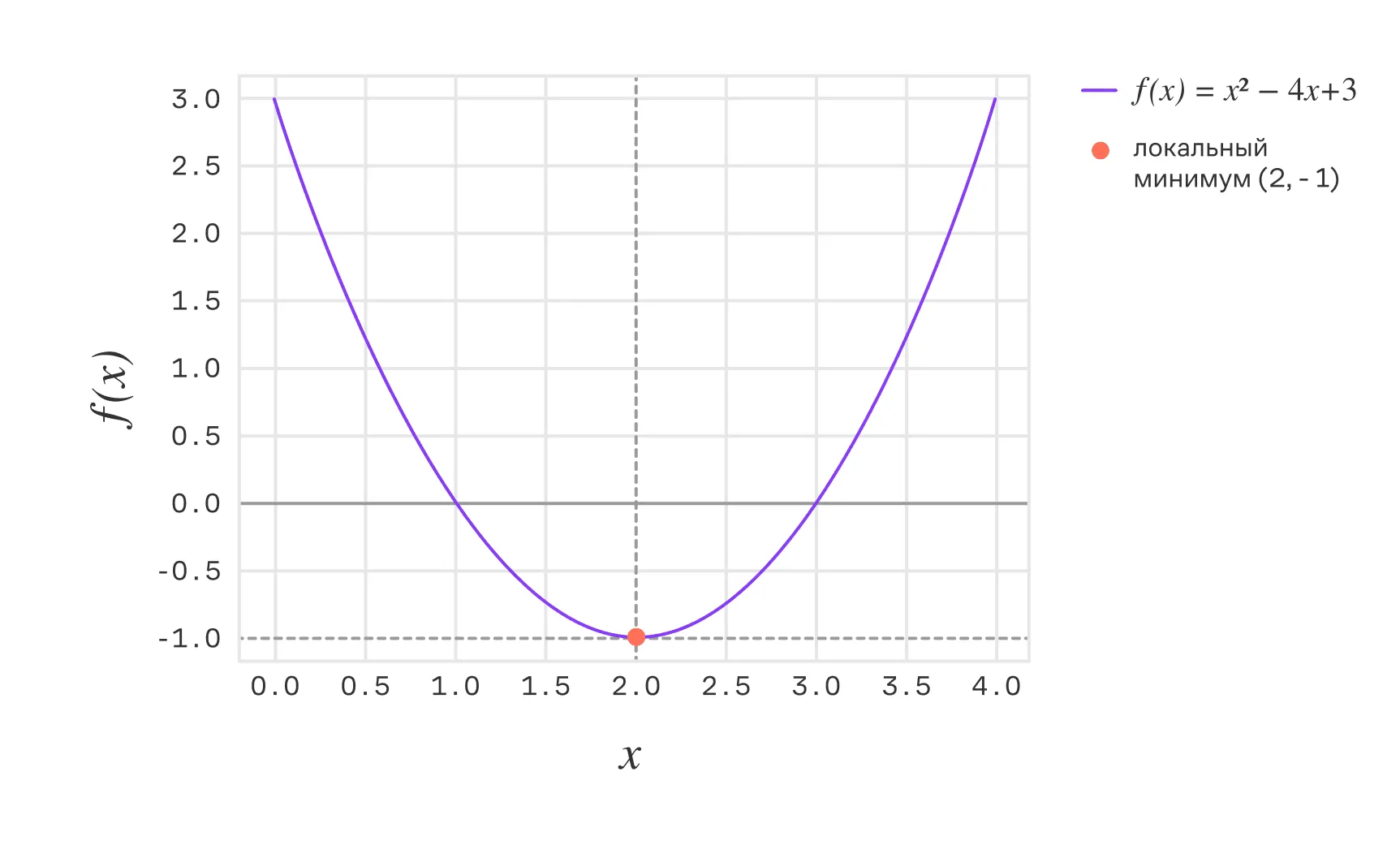
Таким образом, функция достигает локального минимума в точке , где её значение равно . На интервале функция убывает, а на интервале — возрастает.
Производные — это инструмент, который помогает понять, как ведёт себя функция, находить её максимумы и минимумы, а также принимать взвешенные решения.
Вы уже узнали, что такое производная функции одной переменной, каков её геометрический и физический смысл, познакомились с основными правилами дифференцирования и научились их применять.
Эти знания — основа для понимания сложных алгоритмов и моделей, которые используются в анализе данных и машинном обучении. Оптимизация с помощью производных — это не просто математика, а универсальный метод решения задач в разных сферах.
Переходите к квизу и задачам, чтобы закрепить изученный материал. Это поможет вам лучше понять, как производные и оптимизация применяются в реальных сценариях.


