В этом параграфе мы разберём, что такое системы линейных уравнений (СЛУ), каких видов они бывают и как их можно эффективно решать с помощью алгоритма Гаусса.

Но самое главное — мы разберёмся, зачем вообще всё это нужно. Ведь системы линейных уравнений лежат в основе огромного числа прикладных задач анализа данных: от обучения линейной регрессии до оптимизации параметров в нейросетях.

Каждый раз, когда мы хотим наилучшим образом подогнать модель под данные, минимизируя ошибку, задача в итоге сводится к решению СЛУ. Без них было бы невозможно эффективно решать задачи прогноза, факторизации, даже построения графов и вероятностных моделей.

👉 Поэтому понять, как работают СЛУ, — значит научиться видеть скелет большинства алгоритмов машинного обучения.

Определение

Система линейных уравнений (СЛУ) — это набор уравнений и неизвестных переменных, где в каждом уравнении каждая переменная входит только в первой степени и не перемножается с другими переменными.

Также выделяют однородную систему линейных уравнений (ОСЛУ), где вектор свободных членов (число без переменных в правой части уравнений) состоит из нулей.

В предыдущей главе мы уже познакомились с векторами и матрицами, поэтому удобно будет представить СЛУ с их помощью: , где — это матрица коэффициентов , — вектор неизвестных, — вектор свободных членов. Также выделяют расширенную запись системы .

Рассмотрим, какими бывают системы линейных уравнений с точки зрения количества решений, а также приведём конкретные примеры для каждого из видов систем.

Виды систем линейных уравнений

Все системы линейных уравнений можно разделить на три вида относительно их количества решений:

1. Нет решений.
2. Одно решение.
3. Бесконечно много решений.

Давайте рассмотрим базовый случай, когда СЛУ содержит одно уравнение и одну неизвестную:

• (нет решений)
• (одно решение)
• (бесконечно много решений)

Теперь рассмотрим более интересный случай: в пространстве каждое уравнение задаёт прямую, а решение СЛУ — точка их пересечения. Рассмотрим несколько численных примеров для наглядности.

Несовместная СЛУ — нет решений:

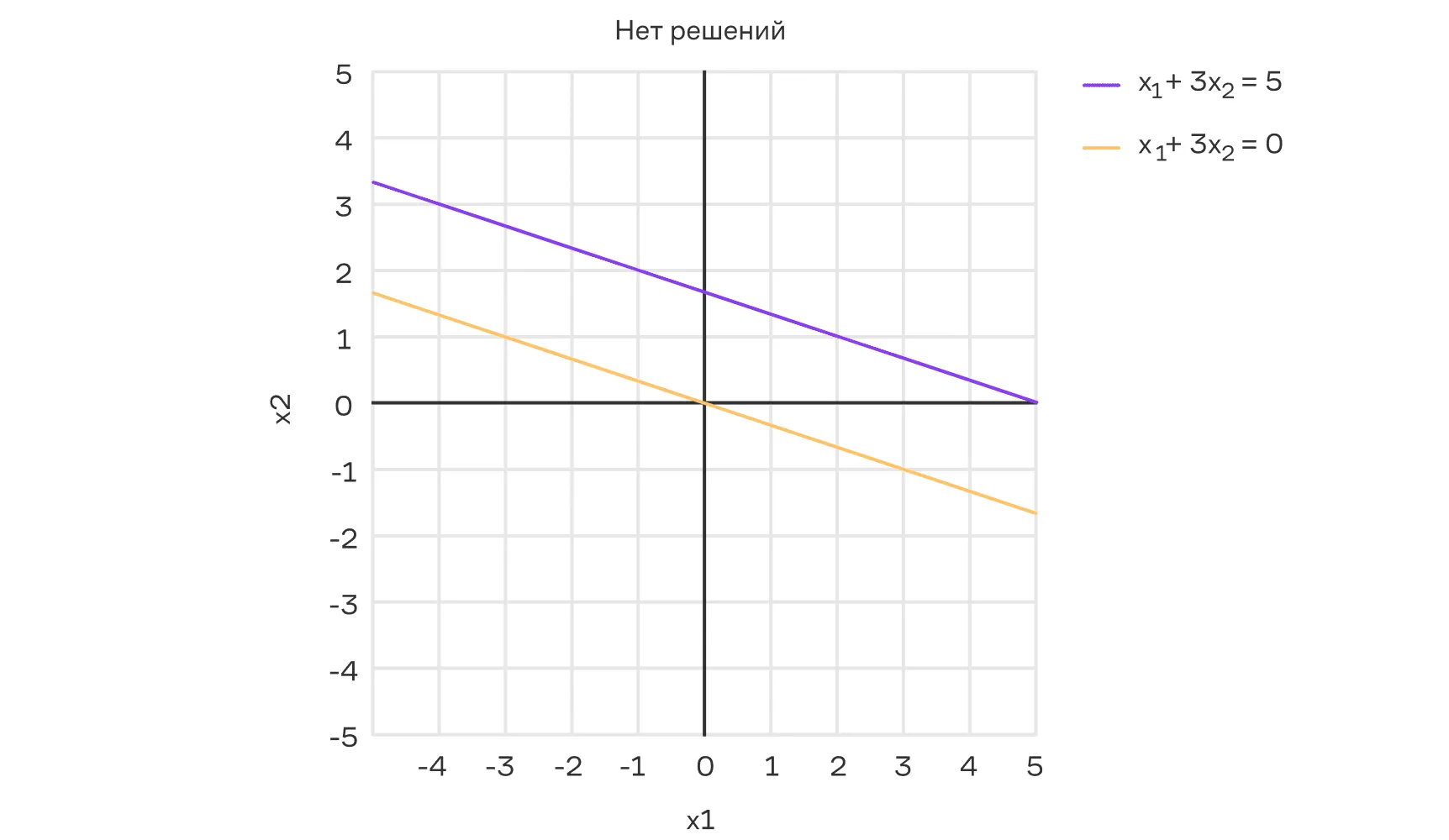
Совместная СЛУ (определённая) — имеет ровно одно решение:

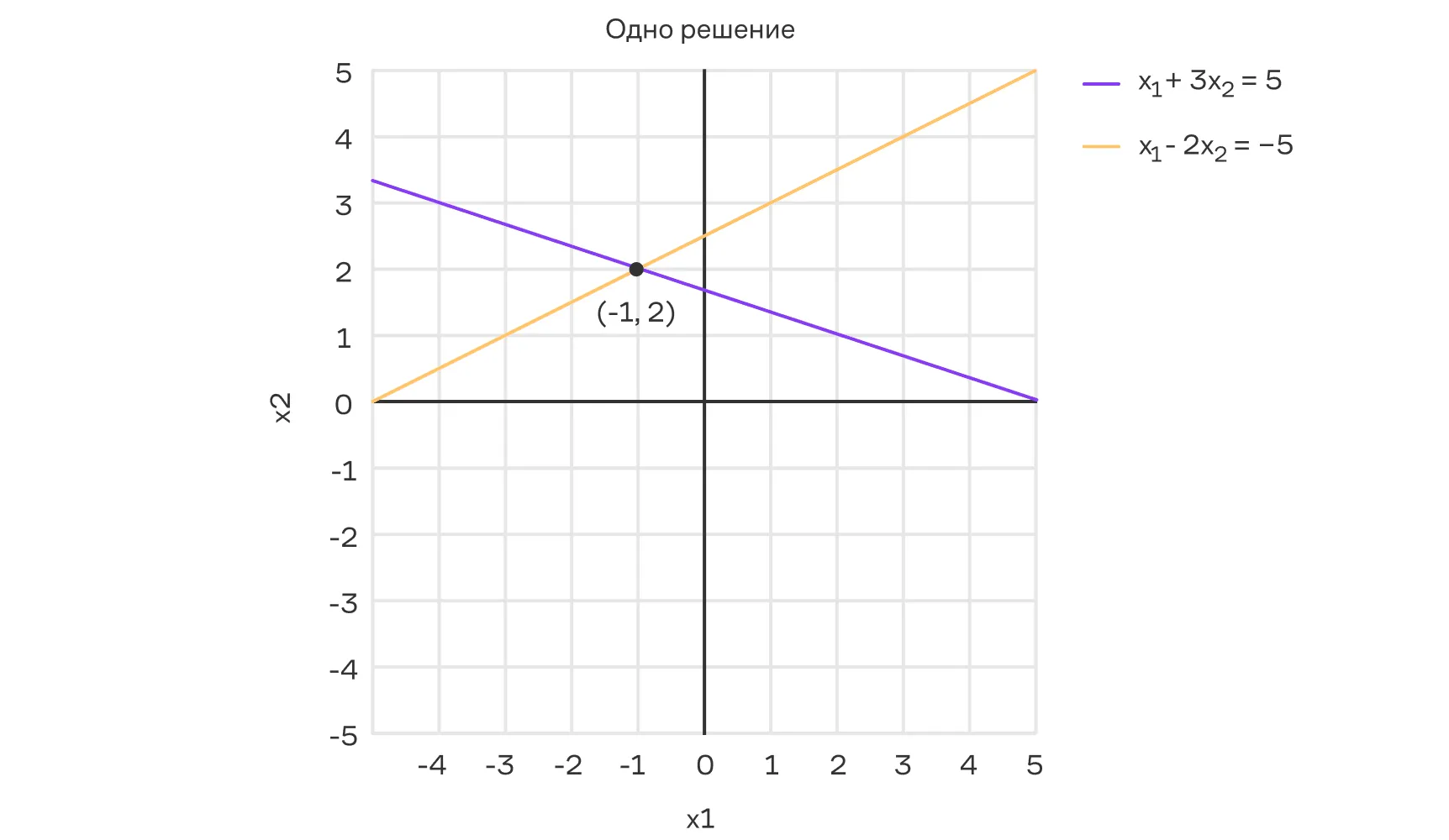
Совместная СЛУ (неопределённая) — имеет бесконечно много решений:

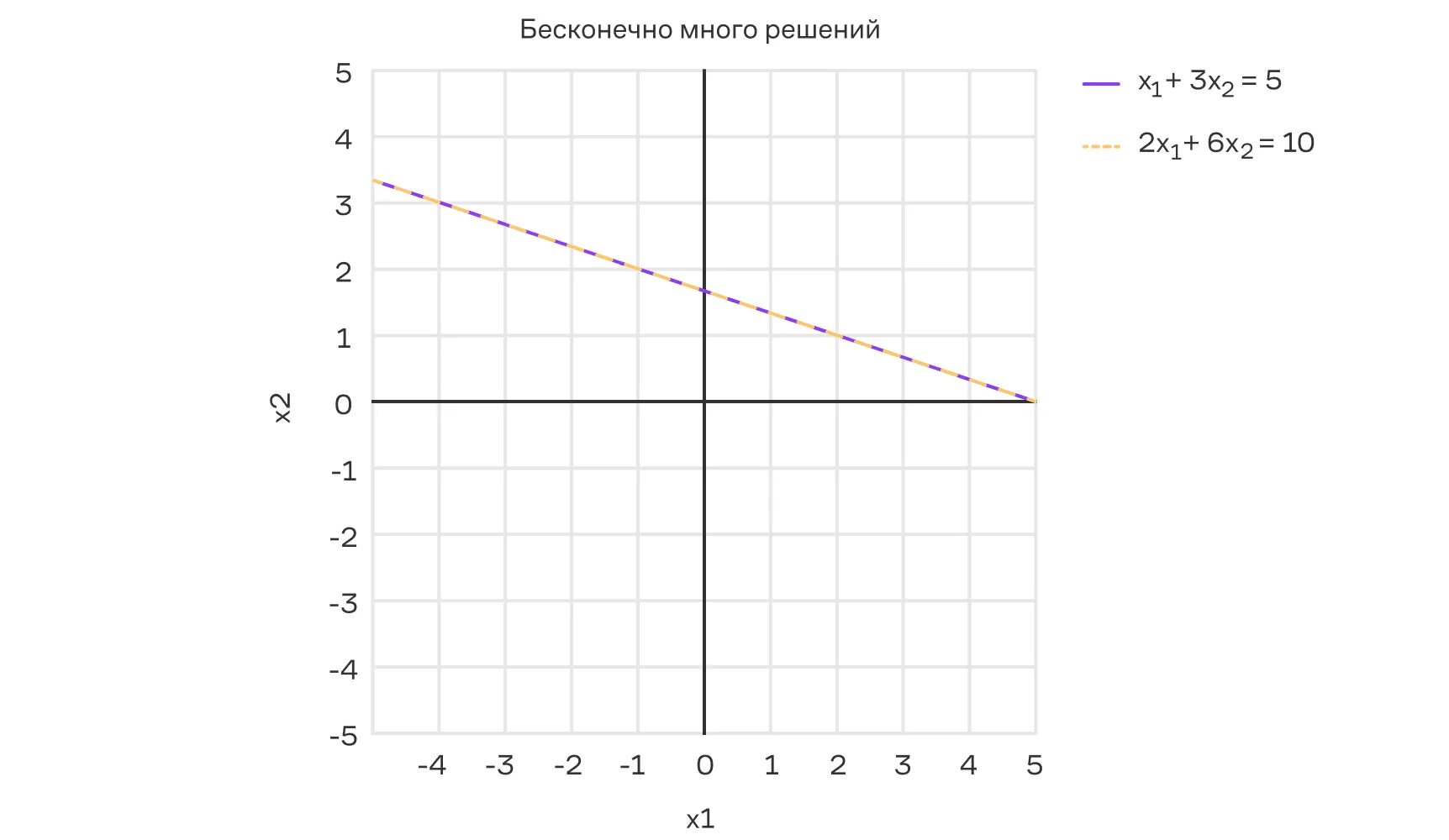
В машинном обучении с каждой из трёх ситуаций мы сталкиваемся постоянно.

• Нет решений (несовместная СЛУ) ­— классический признак переопределённой модели с жёсткими ограничениями. Например, когда мы пытаемся подобрать точно совпадающее значение параметров под все заказанные бизнес‑метрики сразу.
• Одно решение ­— идеальный сценарий в обычной линейной регрессии без мультиколлинеарности, то есть без линейно зависимых признаков в матрице.
• Бесконечно много решений появляется, когда признаков сильно больше наблюдений (типичная широкая матрица в NLP или CV). Здесь и рождаются методы регуляризации (L2, L1, Dropout‑like шумы) — они выбирают единственное «наиболее простое» решение из бесконечного семейства.

Прежде чем двинуться дальше, давайте чуть остановимся. Как вы думаете, возможен ли случай, когда СЛУ имеет ровно два решения?

Двигаемся дальше. Теперь поговорим о том, как решать системы линейных уравнений. Основной метод — это алгоритм Гаусса. Давайте разберём его подробнее.

Алгоритм Гаусса

Цель данного алгоритма заключается в том, чтобы с помощью последовательности элементарных преобразований привести систему к такому «упрощённому» виду, в котором легко описать все её решения или понять, что решений нет.

Чтобы раскрыть метод Гаусса, нужно рассмотреть три аспекта:

• элементарные преобразования, применяемые в этом алгоритме;
• вид, к которому приводится система;
• и сам алгоритм.

Давайте приступим.

Элементарные преобразования

Чтобы уметь переходить от одной системы линейных уравнений к другой без изменения множества решений — то есть так, чтобы все старые решения оставались решениями новой системы и наоборот, — используют следующие элементарные преобразования:

1. Прибавление одной строки к другой с множителем ()

2. Перестановка двух строк

3. Умножение строки на ненулевую константу ()

На практике подобные преобразования часто применяют одновременно (за один шаг) с целью ускорения вычислений. Хороший вопрос заключается в том, почему такие преобразования не меняют множество решений?

Рассмотренные элементарные преобразования можно представить и как умножение исходной матрицы на матрицу слева. Это очень удобно, когда нам нужно структурировано представить операции над матрицами.

1. Прибавление одной строки к другой с множителем (). Пусть — матрица, полученная из единичной, где на позиции элемента строки и столбца стоит .

   Тогда умножение на слева прибавляет строку, умноженную на , к строке матрицы .

2. Перестановка двух строк. Пусть — матрица, полученная из единичной путём перестановки местами и столбцов.

   Тогда умножение на слева переставляет и строки матрицы .

3. Умножение строки на ненулевую константу (). Пусть — матрица, полученная из единичной умножением строки на .

   Тогда умножение на слева умножает строку матрицы на .

Мы рассмотрели, какие бывают элементарные преобразования и как их можно задавать с помощью матриц. Важно отметить, что элементарные преобразования можно выполнять как над строками, так и над столбцами матрицы.

На практике обычно делают преобразования строк, так как в этом случае множество решений СЛУ не меняется. При преобразовании столбцов СЛУ задаётся уже в новых переменных, поэтому и исходное множество решений может измениться.

Далее мы увидим, как элементарные преобразования используются для упрощения структуры матрицы.

Ступенчатый вид

Рассмотрим вид, к которому мы хотим привести матрицу. Важным элементом в матрице при приведении к ступенчатому виду является первый (если смотреть слева направо) ненулевой элемент в каждой строке, который называется ведущим ,опорным или главным элементом. Он используется при исключении неизвестных из остальных строк.

Ступенчатый вид матрицы — это форма записи матрицы, которая удовлетворяет следующим условиям:

• Все ненулевые строки располагаются выше строк, состоящих только из нулей.
• В каждой ненулевой строке ведущий элемент располагается правее ведущего элемента предыдущей строки.

В общем виде матрица после приведения к ступенчатому виду выглядит так:

Где * — это ненулевые элементы в общем случае. Может показаться, что матрица приведенная к ступенчатому виду, — это верхнетреугольная матрица. На самом деле это не совсем так. Отличия заключаются в следующем:

Приведем конкретный пример верхнетреугольной матрицы, которая при этом не соответствует ступенчатому виду:

Пояснение:

• Матрица верхнетреугольная, потому что все элементы ниже главной диагонали равны нулю.
• Матрица не ступенчатая, поскольку в первой строке первый ненулевой элемент стоит во втором столбце, но во второй строке первый ненулевой элемент также стоит во втором столбце. По определению ступенчатого вида, в каждой следующей ненулевой строке ведущий элемент должен идти строго правее ведущего элемента в предыдущей строке — здесь это условие не выполняется.

Но важно отметить, что с помощью элементарных преобразований её легко можно привести к ступенчатому виду — попробуйте сделать это самостоятельно.

Улучшенный ступенчатый вид матрицы — это форма записи матрицы, которая удовлетворяет условиям ступенчатого вида матрицы, а также дополнительно:

• каждый ведущий элемент равен 1;
• в каждом столбце, где находится ведущий элемент, все остальные элементы как выше, так и ниже равны нулю.

В общем виде матрица после приведения к улучшенному ступенчатому виду может выглядеть так (это не полный список всех вариантов):

Где * — это ненулевые элементы в общем случае.

Теперь разберёмся, в чем заключается сам алгоритм, который позволяет с помощью рассмотренных выше элементарных преобразований перейти сперва к ступенчатому, а потом и к улучшенному ступенчатому виду.

👉 На этом этапе у вас уже есть всё необходимое, чтобы составить алгоритм самостоятельно.

Так что, если вам любопытно, советуем сделать паузу и попробовать, а затем сравнить результат.

Алгоритм

В алгоритме Гаусса обычно выделяют два этапа: прямой ход и обратный ход. При этом иногда алгоритмом Гаусса называют только прямой ход, после которого для получения решений из ступенчатого вида системы пользуются обратной подстановкой.

Также иногда отдельно выделяют алгоритм Гаусса — Жордана, в котором прямой и обратный ход реализуются одновременно. Далее, чтобы избежать коллизии в терминологии, давайте будем рассматривать именно алгоритм Гаусса, в котором реализуются прямой и обратный ход за два отдельных шага.

Прямой ход — мы зануляем элементы в столбцах, приводя матрицу системы к ступенчатому виду.

1. Выбирается первый столбец, в котором среди ещё не обработанных строк обнаруживается ненулевой элемент.
2. Строка с таким ненулевым элементом меняется местами с первой из ещё не обработанных строк и далее считается текущей строкой.
3. Из каждой из оставшихся ещё не обработанных строк (стоящих ниже текущей строки) вычитают текущую строку, умноженную на соответствующий коэффициент, чтобы занулить все элементы в выбранном столбце под ведущим элементом.
4. Шаги 1–3 повторяются для каждого следующего столбца справа. Если в каком-то столбце среди непройденных строк ненулевых элементов нет, сразу перейти к следующему.

Разберем прямой ход алгоритма на примере системы из трёх уравнений и четырёх неизвестных, записанной в общем виде.

Примечание:

1. При переходе от одной матрицы к другой у нас будут меняться некоторые коэффициенты, но давайте оставим им прежние имена, чтобы не усложнять запись.
2. Будем считать, что подчёркнутые элементы не равны нулю, чтобы можно было на них делить.
3. Будем обозначать -ю строку как для обозначения элементарных операций со строками. Например, запись означает, что из второй строки вычитается первая строка, умноженная на , и полученный результат записывается в качестве второй строки.

Действие №1:

Действие №2:

Действие №3:

В результате получаем расширенную матрицу, записанную в ступенчатом виде. Ранее мы сказали, что в каждой ненулевой строке первый ненулевой элемент называется ведущим. В данном случае такими элементами будут: .

Остальные ненулевые элементы (переменные и коэффициенты при них) называются свободными. Также важно понимать, что в ходе операций со строками некоторые из ведущих элементов могли занулиться, — например, возможны такие случаи:

В первом случае ведущими элементами будут , а во втором — . При этом после выполнения элементарных операций возможны и другие случаи, кроме приведённых выше.

Обратный ход — после прямого хода матрица системы оказывается в ступенчатом виде, и теперь мы приводим её к более простому виду, который называют улучшенным ступенчатым видом. На этом этапе легко найти все решения или показать, что их нет.

Применяя прямой ход алгоритма, мы получили:

Действие №1:

Действие №2:

Действие №3:

Действие №4:

Стоит отметить, что при некоторых действиях какие-то коэффициенты могли занулиться. Но мы осознанно считали их ненулевыми, чтобы рассмотреть наиболее общий случай. Для двух других специальных случаев, полученных после прямого хода, мы бы получили соответственно:

Остался последний вопрос, который мы не раскрыли в алгоритме Гаусса, — это как из полученной матрицы в улучшенном ступенчатом виде получить решения системы.

Получение решений

В полученной системе у нас есть свободная переменная — , то есть мы можем назначить ей любое значение. Поэтому выберем переменную как параметр и выразим главные переменные через неё:

Тогда решения имеют вид:

Для двух других специальных случаев, полученных после обратного хода, мы бы получили соответственно:

Главные переменные — , а — свободная.

Получили противоречие , то есть система несовместна и решений нет.

Общее правило следующее:

1. Если на этапе прямого хода получилась строка вида , где , то решений не существует, система несовместна.
2. Иначе (система совместна):
   1. Если количество главных переменных равно количеству неизвестных, тогда получаем одно единственное решение, так как все переменные восстанавливаются однозначно.
   2. Если есть свободные переменные, то решений бесконечно много — каждую свободную переменную можно выбрать произвольно, а остальные выразить через неё.

Давайте рассмотрим по одному конкретному примеру для каждого случая.

Пример №1

Выполним алгоритм Гаусса:

Запишем решение:

Получили, что является свободной переменной. Поэтому система имеет бесконечное множество решений.

Пример №2

Выполним алгоритм Гаусса:

Запишем решение:

Получили, что количество главных переменных равно количеству неизвестных, поэтому все переменные восстанавливаются однозначно.

Пример №3

Выполним алгоритм Гаусса:

На этапе прямого хода мы получили строку вида , то есть система несовместная, поэтому решений нет.

Алгоритм Гаусса в Python

Мы рассмотрели, как можно решать СЛУ, используя для этого алгоритм Гаусса. Давайте также разберёмся, как это можно делать в Python c помощью уже знакомых нам библиотек numpy и scipy.

1import numpy as np
2
3# Матрица коэффициентов
4A = np.array([
5    [1, 1, 1],
6    [2, -1, 3],
7    [-1, 4, 2]
8], dtype=float)
9
10# Вектор свободных членов
11b = np.array([6, 8, 10], dtype=float)
12
13# Решаем систему Ax = b
14x = np.linalg.solve(A, b)
15
16print("Решение системы (x, y):", x)
17
18# Output:
19# Решение системы: [2. 2. 2.]

1import numpy as np
2import scipy
3
4# Матрица коэффициентов
5A = np.array([
6    [1, 1, 1],
7    [2, -1, 3],
8    [-1, 4, 2]
9], dtype=float)
10
11# Вектор свободных членов
12b = np.array([6, 8, 10], dtype=float)
13
14# Решаем систему уравнений Ax = b
15x = scipy.linalg.solve(A, b)
16
17print("Решение системы:", x)
18
19# Output:
20# Решение системы: [2. 2. 2.]

Как мы видим, код для решения СЛУ в этих двух библиотеках очень похожий и, более того, внутри библиотеки используют одни и те же алгоритмы из базовой библиотеки LAPACK. Однако библиотека scipy в сравнении с numpy предлагает больше возможностей, например поддержка разреженных матриц (scipy.sparse.linalg.spsolve) или выбор LAPACK-рутины для соответствующего типа матрицы.

Итак, мы разобрались, как работает алгоритм Гаусса и как с его помощью можно находить решения систем линейных уравнений. Важно заметить, что, несмотря на простоту реализации данного алгоритма, вычислительно он является далеко не самым эффективным.

Поэтому на практике при работе с большими объёмами данных алгоритм Гаусса обычно не используется в явном виде. Однако он очень тесно связан с другими более быстрыми алгоритмами (например, LU-разложением) и полезен для понимания работы с матрицами.

В следующем параграфе мы углубим понимание СЛУ: разберём LU-разложения и другие продвинутые методы решения, познакомимся с понятием обратимой матрицы и увидим, как современные библиотеки ускоряют расчёты, сохраняя при этом математическую точность.