В предыдущем параграфе мы научились разговаривать на языке множеств.
В этом — перейдём к подсчётам: соберём базовый набор правил и формул, из которых складывается подавляющее большинство комбинаторных задач.
Что вас ждёт:
- два фундаментальных принципа: правило суммы и правило произведения;
- принцип Дирихле («принцип ящиков») и его применение для быстрых оценок;
- классические конструкции: перестановки, размещения и сочетания — в версиях с повторениями и без них;
- аккуратные связи с алгеброй: биномиальные коэффициенты, треугольник Паскаля и формула бинома,
- мини-кейс из машинного обучения: Weight Agnostic Neural Networks (WANN) и идея эволюционного подбора архитектур (NEAT) как наглядная демонстрация комбинаторного выбора структур без настройки весов.
К концу параграфа вы сможете уверенно переводить текстовые условия в корректные схемы подсчёта, выбирать нужную формулу и быстро прикидывать число вариантов там, где полный перебор невозможен или нецелесообразен.
Начнём с правил и принципов.
Правило суммы
Если объекты выбираются из непересекающихся множеств и , то количество способов выбрать строго один элемент из или из равно .
Простыми словами, сначала мы делаем выбор, из какого множества взять элемент, а затем берём сам объект.
Представим себе ситуацию, в которой занудный сайт требует добавить ещё один символ к паролю, поскольку его длина слишком мала. Разрешены либо цифры (10 штук), либо буквы в нижнем регистре (33 штуки). Тогда всего мы можем выбрать из вариантов. Обратим внимание, что, добавляя лишь один символ, мы увеличиваем количество возможных комбинаций в раза — именно столько различных вариантов продолжить исходный пароль у нас есть.
Правило произведения
Но что, если нам нужно выбрать не один элемент, а несколько?
Например, нужно выполнить последовательность из двух действий: сначала выбрать объект из множества мощностью в элементов, а затем объект из множества мощностью . Независимо от того, пересекаются ли множества, общее число способов будет произведением .
Обратим внимание, что правило произведения вторит декартову произведению: любой возможный выбор будет одной из пар из множества .
Если же нужно выбрать сразу из нескольких множеств, то общее количество вариантов есть произведение мощностей множеств. Для примера давайте оценим количество уникальных автомобильных номеров привычного всем формата «буква, цифра, цифра, цифра, буква, буква» для одного региона. Множество букв включает 12 элементов (т. к. они должны читаться и за рубежом), множество цифр — 10. Следовательно, общее количество уникальных номеров составляет
Снова видим, что с помощью правила произведения легко посчитать мощность декартова произведения множеств.
Принцип Дирихле
Также мы не можем не упомянуть один из наиболее известных принципов в комбинаторике — принцип Дирихле, его ещё называют принципом ящиков.
Принцип Дирихле гласит: если у вас есть больше объектов, чем ячеек, то хотя бы в одной ячейке должно оказаться два объекта. Или, более формально, если объектов распределить по ячейкам, то хотя бы в одной ячейке окажутся два объекта.
Принцип Дирихле может показаться очевидным, или, как говорят математики, тривиальным, но в сложных задачах он зачастую помогает перейти от нетривиальных рассуждений (например, геометрических) к элементарной арифметике.
Для иллюстрации давайте рассмотрим простую задачку, которая когда-то встречалась на собеседованиях:
Докажите, что если взять пять случайных точек внутри квадрата , то найдутся хотя бы две на расстоянии .
Если у вас нет опыта решения подобных задач, то она поначалу может завести в тупик. Но здесь нам как раз поможет принцип Дирихле.
Для удобства нарисуем квадрат:
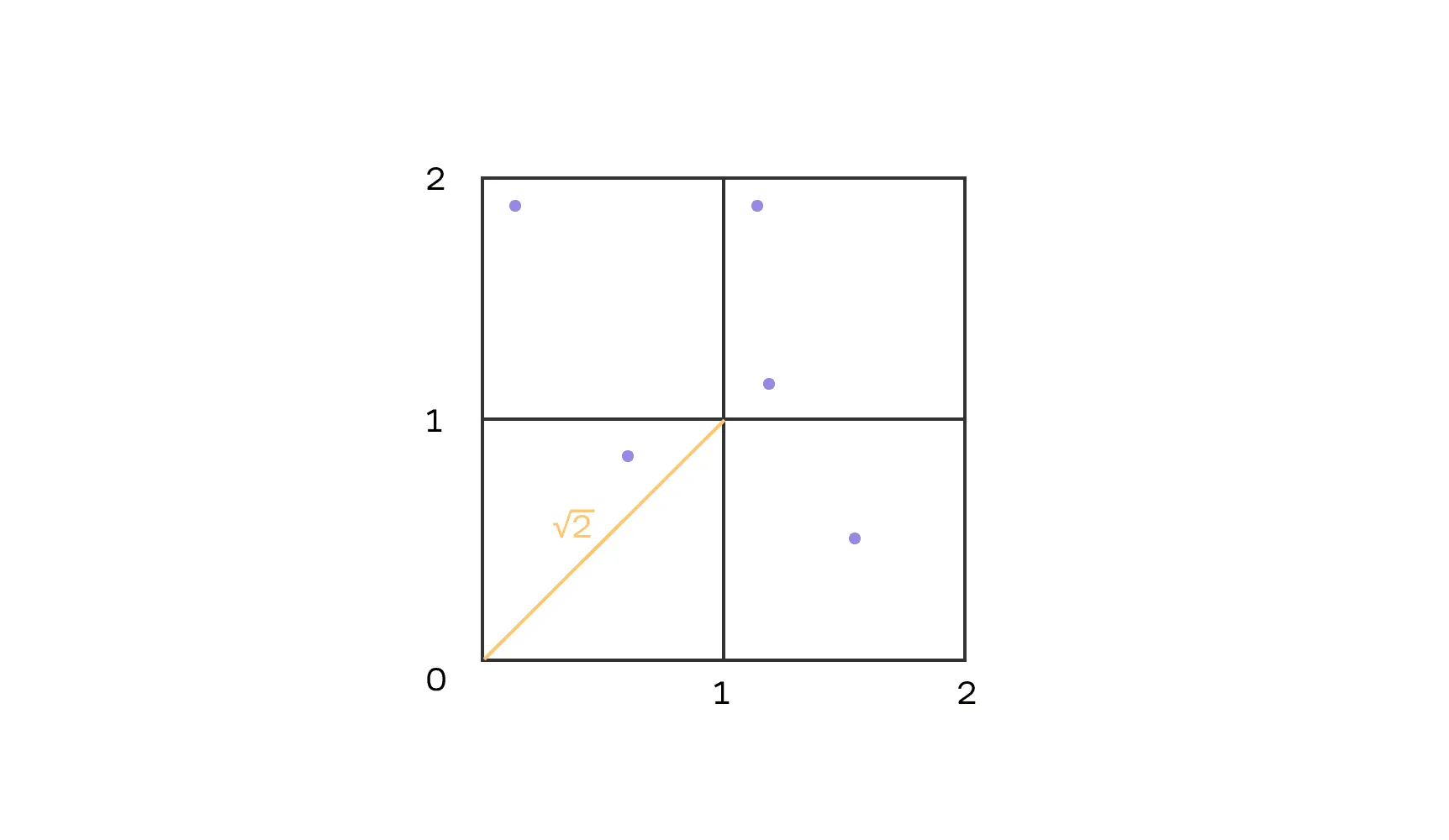
Обратим внимание, что размеры квадрата , т. е. он разделяется на четыре единичных квадрата. Так что если внутри квадрата лежат пять точек, то хотя бы две из них попадут в один квадрат — это и есть принцип Дирихле.
Далее решение становится тривиальным. Максимальное расстояние между двумя точками в единичном квадрате достигается, если они лежат в противоположных вершинах и расстояние между ними равно — длина диагонали единичного квадрата. Следовательно, расстояние между хотя бы одной парой точек не превышает .
Размещения, сочетания и перестановки
Теперь перейдём к понятиям сочетаний, размещений и перестановок. Обычно именно они ассоциируются со словом «комбинаторика» у людей, когда-то её изучавших. И зачастую они вызывают тоску, т. к. все эти верхние и нижние индексы лишь путают.
Но на самом деле эти числа лишь мощности множеств, которые достаточно просто подсчитать, если вы уже познакомились с операциями над множествами, которые мы обсуждали выше.
Количество перестановок
Ранее мы говорили про неупорядоченные множества. Но в некоторых случаях порядок играет роль — например, при выборе победителей олимпиады для участников крайне важно, кто получил золотую медаль, а кто — бронзовую. Так что для начала рассмотрим понятие перестановок.
💡
Количеством перестановокдля множества из элементов называется количество способов упорядочить его элементы. Важно заметить, что все элементы множества считаются уникальными.
Оценить количество перестановок для множества мощностью достаточно просто:
- Первый элемент мы можем выбрать способами.
- Второй — способами: нам доступны все элементы, кроме выбранного на первом шаге.
- Третий — способами.
- Последний — единственным способом.
Получается, общее число перестановок равно:
Здесь мы впервые явно знакомимся с понятием факториала. В рамках комбинаторики будем рассматривать факториал лишь для чисел из множества .
По определению, для натурального числа факториал есть перемножение всех натуральных чисел от до включительно.
Факториал для равен единице:
Например, в классе всего из человек возможно вариантов построений на физкультуре!
Количество размещений
Пусть нам необходимо выбрать элементов из множества без повторений, порядок которых важен. Все элементы множества уникальны, т. е. они не могут повторяться.
💡
Количеством размещений(читается « из по ») называется количество способов выбрать элементов из множества мощностью , порядок которых важен.
Например, вариантами можно выбрать топ-3 участников олимпиады с учётом их места — золотая, серебряная и бронзовые медали — из 100 человек. Далее мы явно посчитаем количество размещений для этого примера.
Для оценки числа размещений из по без повторений можно воспользоваться простой арифметикой: каждый раз выбирая элемент, мы сужаем область выбора, уменьшаем множество, из которого выбираем, на элемент. Мы можем воспользоваться правилом произведения:
Обычно число размещений записывают именно в виде финальной формулы через факториал.
Так, в примере выше мы хотели оценить количество способов выбрать трёх победителей из 100 участников соревнований:
Заметим, что количество перестановок можно обнаружить как частный случай количества размещений: если рассматривать размещения из элементов для множества мощностью , получится как раз число перестановок:
Количество сочетаний
Пусть теперь нам необходимо выбрать элементов из множества без повторений, порядок которых не важен. Все элементы множества уникальны, т. е. они не могут повторяться.
💡
Количеством сочетанийназывается количество способов выбрать элементов из множества мощностью , порядок которых не важен.
Обратите внимание, что различие между количеством размещений и сочетаний заключается лишь в том, важен ли порядок выбираемых элементов. В остальном они совпадают друг с другом.
Для множества мощностью доступно перестановок, а значит, каждое сочетание соответствует различным размещениям. Тогда число сочетаний можно вычислить как:
Упрощая, в примере выше мы выбрали топ-3 участников олимпиады. Для этой одной тройки (сочетания участников) есть способов распределить медали (разместить участников).
Так, например, пять случайных членов сборной университета по настольному теннису можно выбрать способами:
Если внимательно посмотреть на количество сочетаний , можно заметить, что оно позволяет оценить количество всех возможных подмножеств мощностью для множества мощностью .
В качестве упражнения давайте выведем рекуррентную формулу для сочетаний. Пусть нам доступно сочетание длиной из возможных элементов. Выберем отдельный элемент из множества, пусть это будет элемент . Тогда все сочетания делятся на два класса:
- Содержащие элемент . Таких сочетаний может быть , т. к. один элемент уже зафиксирован и в исходном множестве осталось элементов.
- Не содержащие элемент . Таких сочетаний может быть , т. к. один из элементов исходного множества не используется.
Т. к. эти два случая покрывают все возможные ситуации (элемент либо присутствует, либо нет), верна рекуррентная формула для количества сочетаний:
Также стоит обратить внимание на симметрию числа сочетаний, а именно:
ведь при выборе элементов из множества мощностью не выбранными остаются элементов. Иначе говоря, мы делим множество на две части размерами и . Логично, что количество способов такого разделения одинаковое для левой и правой части. Этот факт также очевиден из самой формулы числа сочетаний: в знаменателе стоят и , смена порядка которых не приводит к изменениям.
Сочетания с повторениями
В некоторых ситуациях один элемент можно выбрать несколько раз. На практике сочетания с повторениями встречаются не так часто, но в качестве иллюстрации может служить метод бутстрапа, который вы встретите или уже встречали в статистике.
Если коротко, бутстрап позволяет генерировать новые выборки на основе существующих путем выбирания элементов с возвращением. Порядок элементов в бутстрапированной выборке не важен, один и тот же элемент исходной выборки может попасть в бутстрапированную несколько раз.
Например, для создания бутстрапированной выборки размером из общей выборки размером каждый раз мы выбираем случайный объект из исходной выборки и «возвращаем» его на место, т. е. можем выбрать ещё раз. Таким образом, у нас могут получиться следующие бутстрапированные выборки:
- ,
- ,
- и даже .
Для оценки числа сочетаний с повторениями можно воспользоваться следующей формулой:
Доказательство этого факта требует введения дополнительных теорем и опущено в данном повествовании. Если вы хотите с ним ознакомиться, это можно сделать, например, здесь.
Размещения с повторениями
Размещения с повторениями обозначаются как . Предполагается, что при каждом выборе элемент также «возвращается» обратно в исходное множество и может быть выбран снова.
Для разминки докажем, что число размещений с повторениями вычисляется как
Для этого рассмотрим упорядоченный набор размером в элементов, из исходного множества размером . Отдельно обратим внимание на первый элемент и на все оставшиеся:
- Первый элемент мог быть выбран способами.
- Оставшиеся элементы в количестве штук представляют собой один из вариантов размещения элементов из множества элементов, т. е. могут быть выбраны способами согласно определению.
Следовательно,
Для случая видим, что один элемент можно выбрать ровно способами, следовательно, общее число размещений с повторениями по индукции равно:
Что и требовалось доказать.
Для иллюстрации данного факта вновь обратимся к паролям. Пусть нам доступен алфавит из элементов и мы хотим посчитать число уникальных паролей длиной . Символы могут повторяться и в общем случае вообще никак не зависят друг от друга.
А значит, каждый символ в пароле может быть выбран способами, а для пароля длиной мы получаем вариантов пароля. С другой стороны, число паролей длиной в алфавите из символов — это и есть число размещений с повторениями .
Например, если мы говорим только про цифры, то уникальных числовых паролей длиной в символа всего , а именно они использовались на мобильных телефонах до недавних пор. Сейчас же по умолчанию используются пароли длиной в шесть символов, и число комбинаций уже .
Рассмотрим, как меняется сложность пароля в зависимости от его длины и размера алфавита. Например, пароль в алфавите из 26 символов — английский алфавит в нижнем регистре — длиной в 8 символов примерно соответствует по «стойкости» паролю из 6 символов, который использует латиницу нижнего и верхнего регистра, а также цифры.
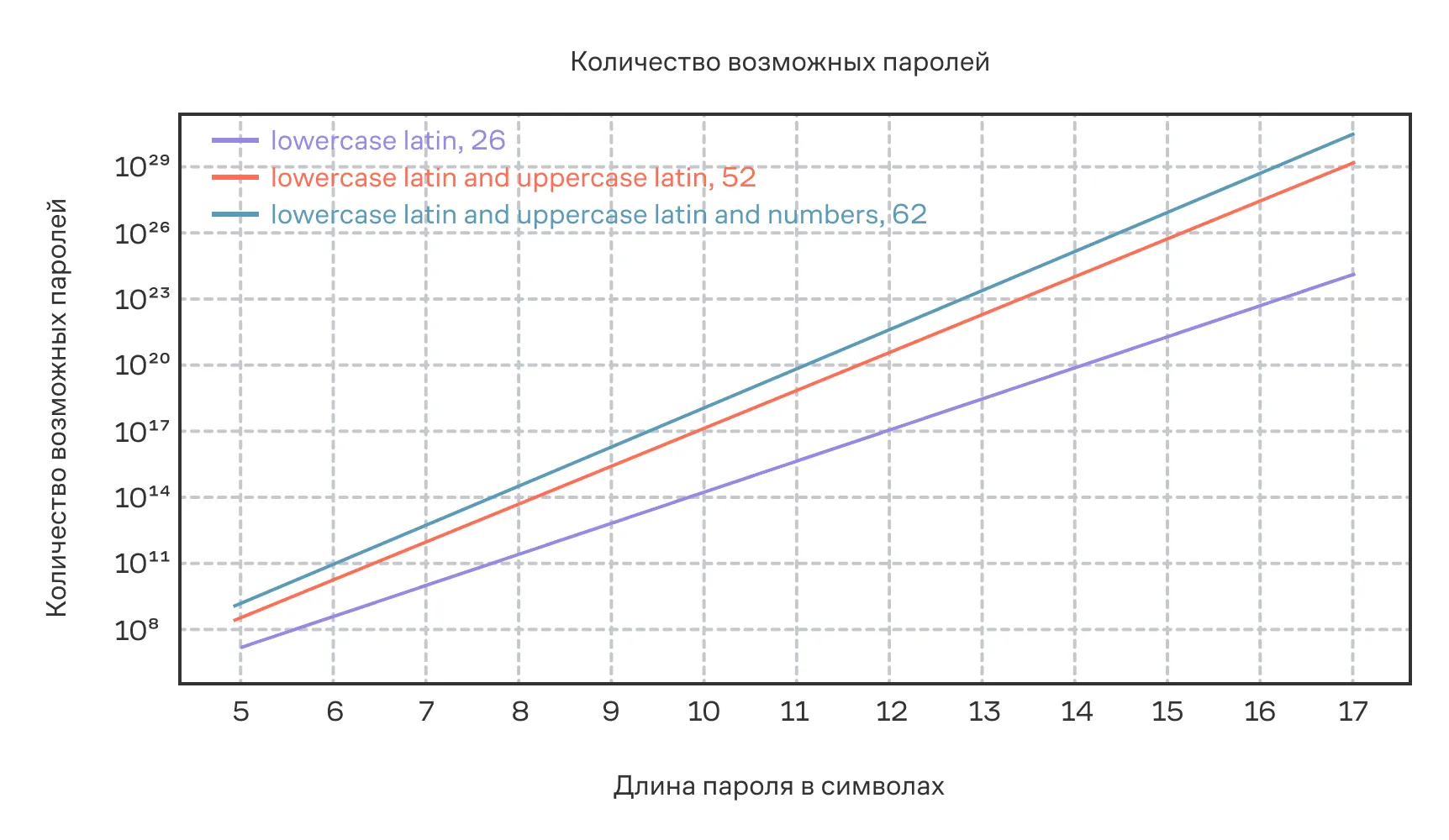
Из графика легко увидеть, что увеличение длины пароля даже на один символ увеличивает количество возможных комбинаций в раз и, соответственно, повышает безопасность пароля. Правда, люди обычно используют слова или значимые даты, что существенно снижает безопасность, но это уже вопрос психологии и криптографии, а потому его опустим.
Сводная таблица перестановок, сочетаний и повторений
Наконец, сведём все рассмотренные в данном параграфе сущности в одну таблицу для вашего удобства.
|
Обозначение |
Термин |
Чему равно |
Порядок важен |
Возможны повторения |
|
|
Перестановки |
|
да |
нет |
|
|
Размещение из по без повторений |
|
да |
нет |
|
|
Сочетание из по без повторений |
|
нет |
нет |
|
|
Сочетание из по с повторениями |
|
нет |
да |
|
|
Размещение из по с повторениями |
|
да |
да |
Особое место среди этих формул занимают сочетания . Как мы уже увидели, они обладают интересными свойствами. Например: они симметричны и подчиняются рекуррентному соотношению. Оказывается, эти свойства связывают комбинаторику с алгеброй через так называемые биномиальные коэффициенты, которые наглядно представляет треугольник Паскаля.
Представьте, что у вас есть алгоритм для генерации всех возможных путей в игре и на каждом шаге игрок может выбрать одно из двух действий, например «идти налево» или «идти направо» После трёх шагов количество возможных исходов равно . Но что, если нас интересует, сколько именно путей содержат ровно два «поворота налево»?
Это задача на биномиальные коэффициенты: число таких путей равно . А если построить треугольник Паскаля, то это число окажется прямо в нужной позиции — и так для любого количества шагов.
Поговорим об этом подробнее!
Биномиальные коэффициенты и треугольник Паскаля
Почти наверняка вы видели треугольник Паскаля в кабинете математики в школе, и его даже могли упоминать на занятиях. Сам треугольник устроен простым образом: он заполняется сверху вниз, края треугольника всегда состоят из единиц, а каждый элемент в новом ряду есть сумма двух ближайших по горизонтали к нему в предыдущем:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
Как мы уже говорили выше, каждый элемент этого треугольника есть биномиальный коэффициент — это , где — номер ряда, а — номер числа в ряде (начиная с ):
Биномиальными коэффициентами они называются потому, что именно с такими коэффициентами встречаются слагаемые различных степеней при возведении суммы в степень. Например, для степени 3:
мы видим, что коэффициенты соответствуют четвертой строке треугольника Паскаля.
В общем случае для суммы двух элементов в произвольной степени будет верна следующая формула:
Выше мы уже доказывали симметрию биномиальных коэффициентов (количества сочетаний) и рекуррентное соотношение для них, но в контексте треугольника Паскаля стоит упомянуть их ещё раз:
-
Биномиальные коэффициенты симметричны , что логично ввиду коммутативности операции сложения: если поменять и местами в формуле выше, то коэффициенты при их степенях не изменятся.
-
Рекуррентное соотношение появляется логичным образом. Если разложить степень суммы на два множителя:
то при раскрытии скобок член будет складываться из двух слагаемых:
где коэффициенты как раз соответствуют биномиальным коэффициентам меньшей степени:
Стоит заметить, что именно рекуррентное соотношение позволяет эффективно вычислять число сочетаний, ведь подсчёт факториалов для больших чисел — нетривиальная задача.
Иллюстрация из мира машинного обучения
Несмотря на то, что в явном виде комбинаторные задачи — не частые гости в мире машинного обучения, иногда они всё же встречаются. И зачастую это очень красивые задачи, которые показывают, как поиск правильной комбинации элементов может быть важнее, чем точная настройка их параметров.
Возможно, вы уже знакомы с понятием нейронных сетей. Если нет, то вы ещё обязательно познакомитесь с ними. Пока же можно просто сойтись на том, что нейронная сеть — это некоторая сложная математическая формула с множеством настраиваемых параметров — весовых коэффициентов. Любую математическую формулу можно представить в виде графа. Например, для функции граф будет иметь вид:
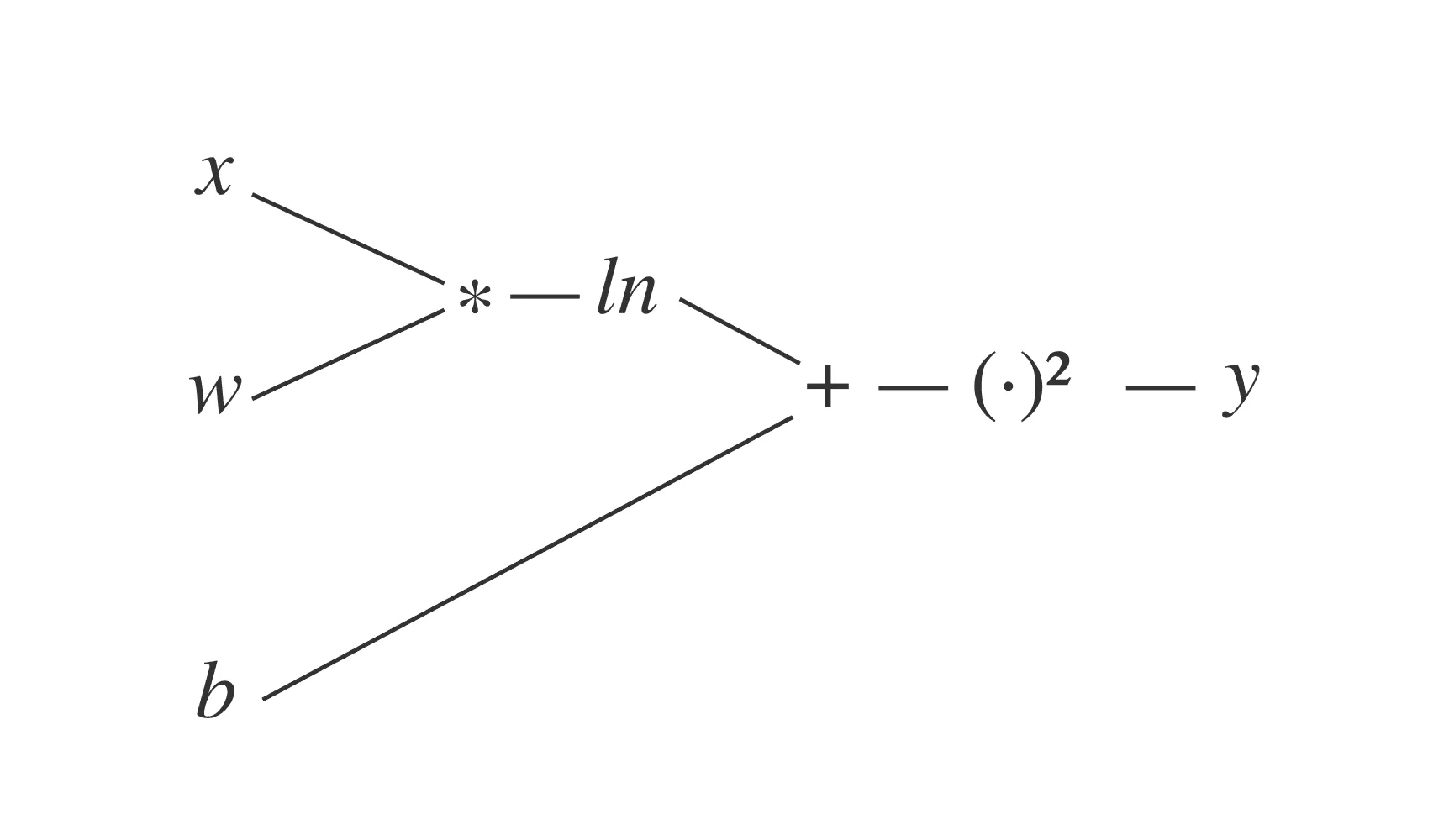
где и — как раз настраиваемые весовые коэффициенты, а — наблюдаемый объект.
Как правило, нейронные сети строятся в виде последовательно расположенных фиксированных блоков, наборов функций, называемых слоями, и настраиваются лишь весовые коэффициенты (или, как их чаще называют, веса).
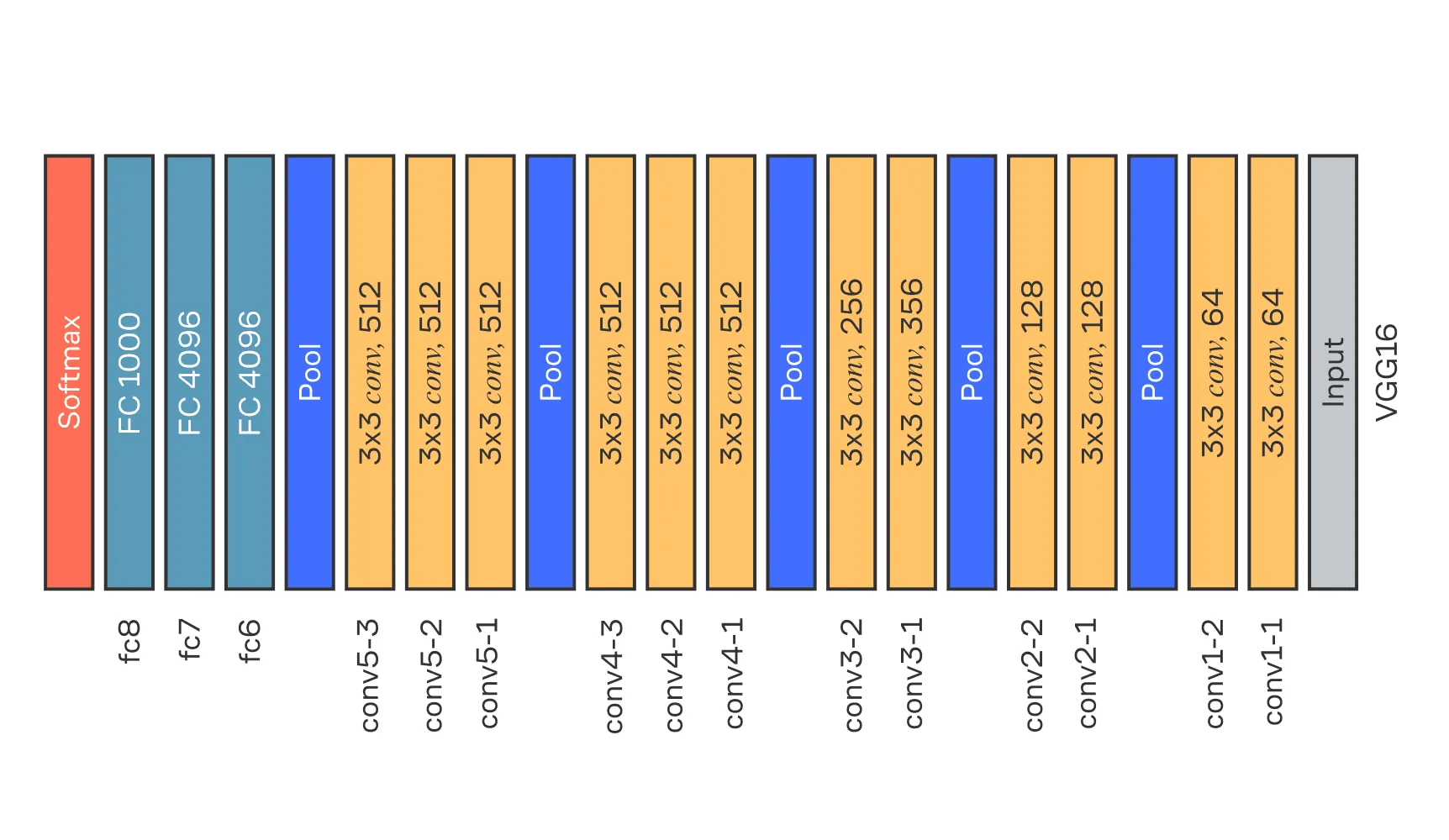
Нейронная сеть VGG-16, представленная в 2013 году. Каждый слой (за исключением входного Input-слоя) задаёт некоторое отображение из входного представления в некоторое промежуточное, латентное представление
Но в 2019 году на конференции NeurIPS была представлена работа Weight Agnostic Neural Networks (WANNs), в которой авторы решили совсем отказаться от настраиваемых весов. Вместо этого они предложили подбирать граф оптимальной структуры, то есть, по сути, искать математическую формулу, описывающую решение задачи, — практически физический закон! Для упрощения на искомое решение накладывалось ограничение: все связи обладают одним и тем же весовым коэффициентом, который задаётся экспертом извне.
Таким образом, нейронная сеть представляла собой набор операций, которые подбирались комбинаторно. Если существенно упростить описание этой процедуры, то она заключалась в следующем:
- На каждом шаге из модели (графа) получалось множество претендентов — либо за счёт добавления новой операции, либо заменой существующей.
- Множество претендентов оценивалось на фиксированной выборке, и лишь лучшие из них оставались для следующей итерации, а остальные удалялись
Внимательный читатель заметит, что это описание напоминает эволюционный алгоритм, и будет прав. В работе использовалась именно его модификация, называемая NEAT (англ. NeuroEvolution of Augmenting Topologies). Главный результат этого подхода заключается в том, что итоговые модели обладали на удивление простой структурой, особенно в сравнении с классическими нейросетями для тех же задач. При этом они обеспечивали качественное и, что важнее, устойчивое решение для задач классификации и обучения с подкреплением.
Мы не будем здесь углубляться в технические детали алгоритма. Желающие могут обратиться к оригинальной статье, но для её понимания мы рекомендуем сперва ознакомиться с этим хендбуком, а затем с хендбуком по машинному обучению.
Ниже — визуализации WANN в действии на двух модельных задачах.
Локомоция двуногого робота (Bipedal Walker)
Необходимо научить двуногого робота ходить, используя информацию с его датчиков: линейную скорость, углы в суставах, наличие контакта с поверхностью, расстояние до препятствия в определённом направлении (lidar) и др.
Как видно на иллюстрации, алгоритм нашёл нейросеть, обладающую очень простой структурой, но при этом успешно управляющую движениями робота.
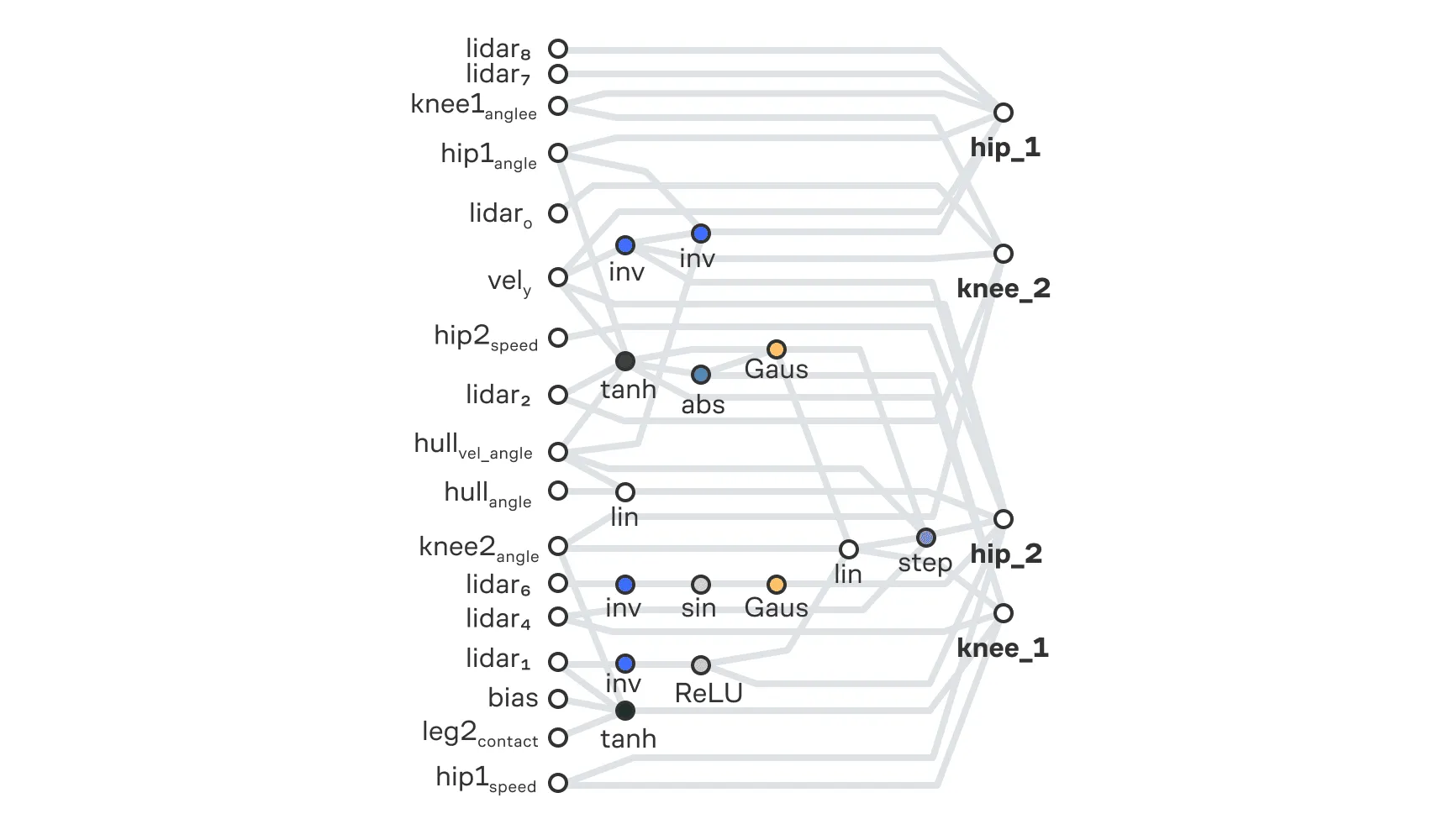
Пример топологии WANN для управления агентом в среде BipedalWalker
На схеме топологии показана найденная архитектура сети, где каждое ребро имеет одинаковый вес, но используются различные функции активации в узлах (tanh, ReLU, sin, abs, inv, Gauss, step). Слева расположены входные признаки, описывающие состояние робота и среды — углы и скорости суставов, данные лидара, контакт ног с поверхностью и т. д. Справа — управляющие выходы, отвечающие за сгибание и разгибание бёдер и коленей.
Просто оцените по видео, как такая минималистичная сеть без настройки параметров справилась с управлением персонажем.

Управление автомобилем в гонках (Car Racing)
Во второй задаче требовалось научить машину проходить гоночную трассу, ориентируясь по данным лидаров, наискорейшим образом. И здесь тоже итоговая архитектура сети оказалась минималистичной, но смогла обеспечить качественное управление.
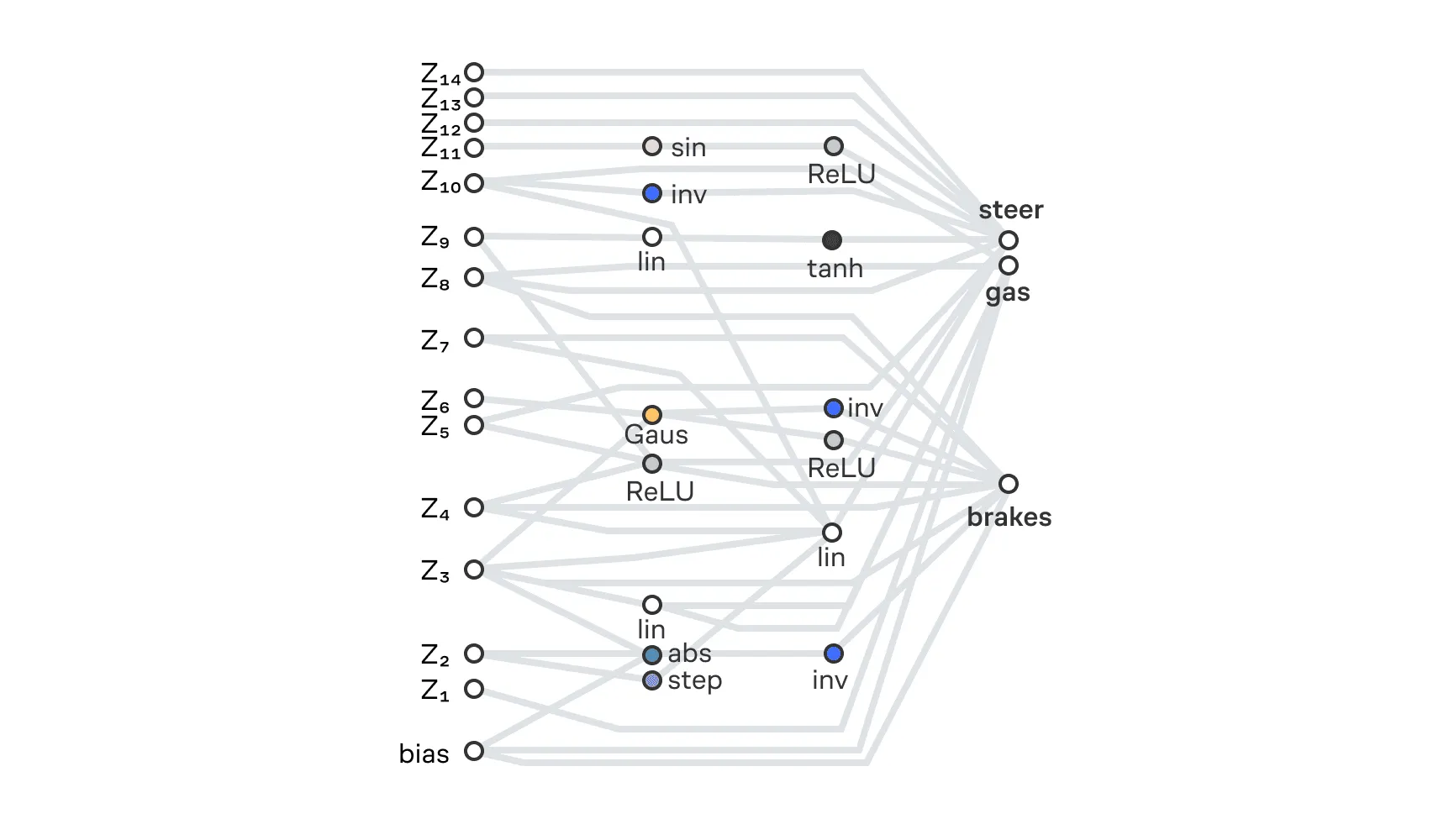
Архитектура WANN для задачи Car Racing
На рисунке изображена итоговая структура сети. Слева подаются входные признаки, включая данные с лидаров (z₁–z₁₃) и дополнительный bias-сигнал. А справа расположены выходы, управляющие поворотом руля (steer), подачей газа (gas) и тормозами (brakes).
Как и ранее, несмотря на отсутствие настройки индивидуальных весов, полученная модель оказалась способной эффективно управлять машиной на гоночной трассе, ориентируясь только по лидарным данным.
Вот демонстрация:

Работа WANN чудесно иллюстрирует применение комбинаторики (и неградиентных методов оптимизации) в машинном обучении — как их возможности, так и ограничения.
С одной стороны, подбор оптимальной архитектуры, как в WANN и NEAT, может привести к простым и устойчивым решениям, даже без настройки весов. С другой, с ростом сложности архитектуры количество вариантов растёт комбинаторно быстро. И вновь мы сталкиваемся с комбинаторным взрывом.
Получается, без введения дополнительных ограничений, использования эвристик, отсечения наименее перспективных решений получить эффективное решение не получится. Именно поэтому базовое понимание комбинаторики важно, ведь оно позволяет оценить сложность задачи и возможные ограничения, с которыми придётся столкнуться.
Короче говоря, комбинаторика — крайне полезная часть арсенала каждого, кто хочет создавать эффективные алгоритмы и модели.
Итак, мы познакомились с основными определениями и понятиями — это фундамент как для комбинаторики и многих других областей:
- правило суммы;
- правило произведения;
- принцип Дирихле;
- шесть классических формул для размещений, сочетаний и перестановок.
Эти понятия пригодятся нам как при работе с графами или статистикой, так и в алгоритмических задачах.
Теперь, вооружившись этим фундаментом, мы готовы решать более сложные задачи.
В следующем параграфе мы узнаем, как избегать двойного счёта при работе с пересекающимися группами объектов с помощью метода включений-исключений. И поймём, как оценить общее число всевозможных комбинаций — например, признаков в машинном обучении — с помощью множества всех подмножеств.



