Комбинаторные приёмы достаточно изящны. Иногда они позволяют найти неочевидное, но очень простое решение для математической задачи. Но гораздо чаще комбинаторика позволяет оценить сложность задачи и потенциального решения и выбрать более подходящий или эффективный вариант.
В этом параграфе мы поговорим о гиперпараметрах:
- что это такое, чем они отличаются от параметров и почему их подбор дороже;
- какие существуют методы подбора гиперпараметров;
- что такое проклятие размерности и комбинаторный взрыв.
К концу параграфа вы сможете прикидывать стоимость перебора, осознанно выбирать стратегию поиска и понимать, когда нужно сужать пространство решений или добавлять структурные предположения.
Приступим!
Гиперпараметры: что это и чем они отличаются от параметров
В машинном обучении можно разделить модели на параметрические и непараметрические.
Примеры параметрических моделей — линейная регрессия, метод опорных векторов, решающее дерево, нейронная сеть. То есть все модели, где настраиваются некоторые параметры (веса, коэффициенты) для лучшего соответствия данным.
Примером непараметрической модели может служить метод ближайших соседей (kNN) — в нём не происходит автоматической настройки чего-либо на основе обучающей выборки.
Помимо параметров, у моделей также выделяют гиперпараметры. Гиперпараметры отвечают за более общие свойства моделей: метрика в kNN, вид регуляризации в линейной регрессии, максимальное число листьев в дереве — это всё гиперпараметры.
💡Основное отличие гиперпараметров от параметров заключается в том, что перед обучением модели (нахождением оптимальных значений параметров) необходимо зафиксировать гиперпараметры.
Гиперпараметры могут быть категориальными (например метрика в kNN), дискретными (число соседей в kNN) или непрерывными (коэффициент регуляризации). Как правило, гиперпараметры выбираются экспертом вручную или же с помощью неградиентных методов оптимизации.
Примечание
Внимательный читатель заметит, что в моделях машинного обучения есть целая иерархия настраиваемых величин.
Например, в ансамблях деревьев нужно выбрать размер ансамбля, а каждое дерево, в свою очередь, обладает собственными гиперпараметрами (например, глубина). Подобные гиперпараметры «более высокого порядка» иногда называют «метапараметрами», но данный термин не является общепринятым и, вообще говоря, не имеет смысла: количество уровней гиперпараметров формально не ограничено сверху (хотя на практике редко встречается больше трёх-четырех).
В некотором смысле даже сам класс используемых моделей можно считать гиперпараметром — например, перед настройкой параметров линейной регрессии нужно принять решение использовать именно линейные модели, а не деревья решений.
Здесь важно отметить, что если мы не выберем гиперпараметры, то, как правило, не сможем настроить параметры — то есть обучить модель. Поэтому проверка каждого набора гиперпараметров требует полного или частичного обучения модели — то есть она крайне затратна для сложных моделей.
Методы подбора гиперпараметров
Существует множество методов подбора гиперпараметров — в этой части мы разберём только основные. Как правило, в сложных задачах используются библиотеки (например, optuna, которую мы рассмотрим дальше) — они объединяют в себе сразу несколько подходов.
Далее мы будем преимущественно рассматривать численные гиперпараметры, т. к. если гиперпараметр категориальный, то его значения не упорядочены и никак не связаны друг с другом, а значит, других вариантов, кроме его прямого перебора, нет.
Поговорим о следующих методах:
- Перебор по сетке (англ. Grid Search).
- Случайный поиск (англ. Random Search).
- Байесовская оптимизация.
А ещё посмотрим, что под капотом у библиотеки optuna.
Перебор по сетке
Пусть для модели доступно гиперпараметров, для -го гиперпараметра задан диапазон допустимых значений . В данном диапазоне выбирается различных значений гиперпараметра. Тогда общее число возможных комбинаций гиперпараметров равно:
Несложно заметить, что количество различных наборов гиперпараметров оценивается как число различных комбинаций элементов из множеств с мощностями .
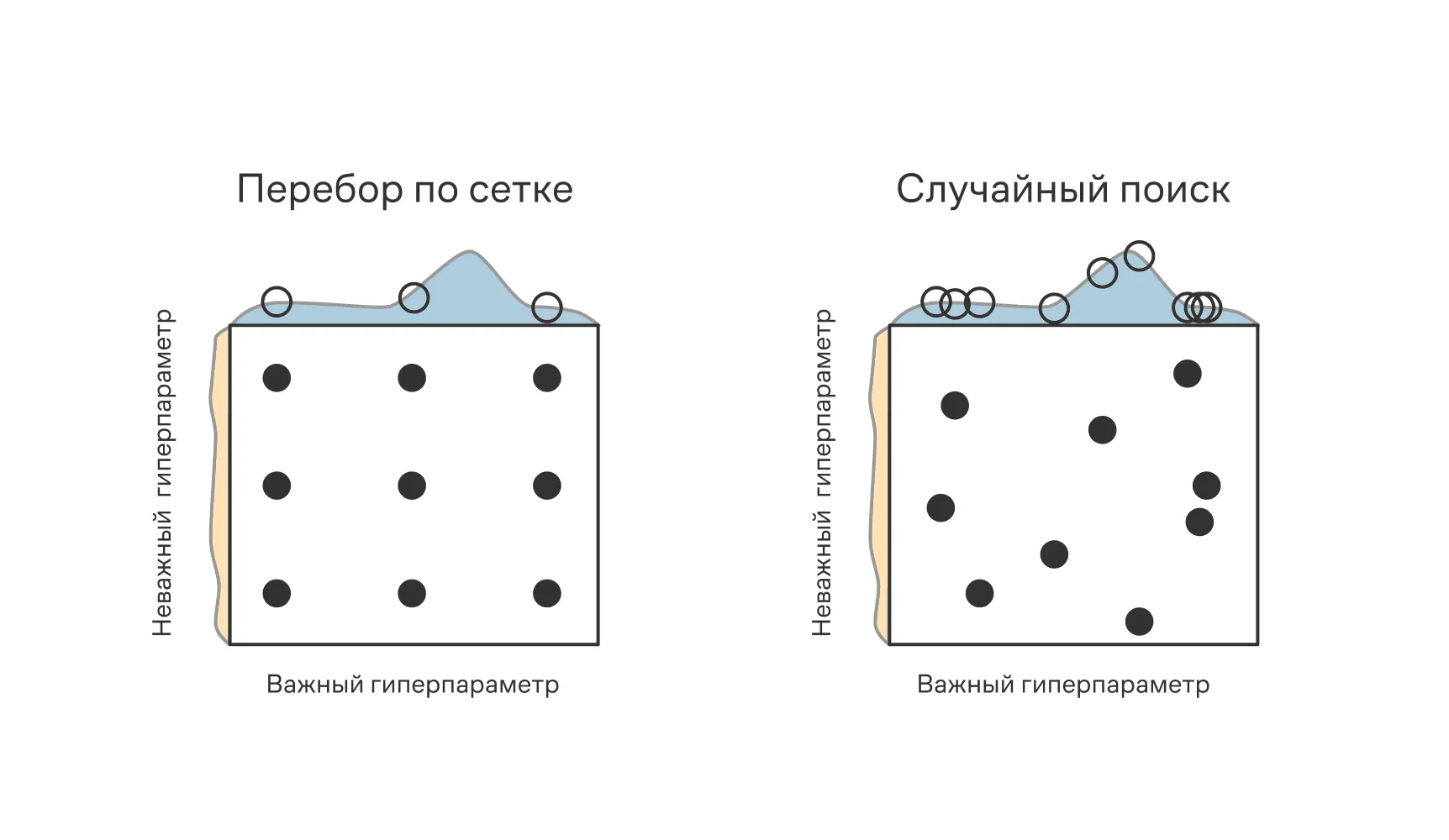
Поиском по сетке такой подход называется потому, что рассматриваемые значения гиперпараметров образуют сеть: каждый узел этой сети соответствует строго одному набору значений гиперпараметров.
На левой иллюстрации мы видим два гиперпараметра, для каждого из которых перебирается по сетке три значения, что суммарно даёт девять различных вариантов, для каждого из которых оценивается качество модели.
На правой иллюстрации также перебирается девять различных комбинаций гиперпараметров, но их значения выбираются случайно в допустимых диапазонах — это случайный поиск.
Например, мы решаем задачу регрессии и нужно выбрать вид регуляризации (, ) если нужно подобрать значения коэффициента регуляризации :
Пусть мы хотим проверить различных значений . Тогда всего нужно будет попробовать вариаций
Шаг сетки не обязательно должен быть одинаковым. Сетка может быть:
- Регулярной. Тогда все отсчёты расположены через равные промежутки. Пусть заданный интервал , тогда шаг будет равен и покроет варианты
- Логарифмической. Тогда значение гиперпараметра представляется в виде , где — некоторое основание, а меняется именно показатель степени. Так, в примере выше выгодно воспользоваться , а варьировать от до , тем самым среди вариантов будут . Такой подход более предпочтителен, если гиперпараметр существенно влияет, например, на оптимизируемый функционал (как в случае с коэффициентом регуляризации), — он позволяет более точно приблизиться к нужному значению за несколько итераций.
- Случайной. О ней расскажем чуть позже.
Важно отметить, что при использовании перебора по сетке не обязательно получать результат сразу. Полезно действовать в несколько шагов, особенно если некоторые гиперпараметры требуют больше внимания, чем другие.
Например, в случае работы с коэффициентом регуляризации можно сначала обнаружить, что оптимальные результаты достигаются при значении коэффициента регуляризации, равном , а затем сформировать новую сетку уже вокруг этого значения.
Задача для самопроверки. Сколько попыток обучения модели необходимо, чтобы перебрать три гиперпараметра, где первый принимает 7 значений, второй — 12, а третий — 4?
Ответ (не открывайте сразу; сперва подумайте сами!)
.
Случайный поиск
Вместо перебора по сетке можно случайным образом выбирать значение гиперпараметра из допустимого промежутка (или множества).
Данный подход работает одинаковым образом как с дискретными, так и с непрерывными величинами, и является рабочей альтернативой перебору по сетке. Работа «Случайный поиск для оптимизации гиперпараметров» (англ. Random Search for Hyper-Parameter Optimization) за авторством Джеймса Бергстры и Йошуа Бенджио (это один из «отцов» современного ИИ, в 2018 году он получил премию Тьюринга) показывает, что случайный поиск позволяет быстрее — за меньшее число итераций — найти оптимальный регион значений гиперпараметров.
Байесовская оптимизация
Если развить идею случайного поиска, получится подход, получивший название байесовской оптимизации (англ. bayesian optimization). Полное понимание байесовской оптимизации требует глубоких знаний в области теории вероятностей и байесовского подхода, поэтому ограничимся кратким обзором.
Пусть гиперпараметры влияют на значение оптимизируемого функционала , а значит, существует условное распределение , которое тем не менее нам не известно. Тогда при каждой попытке обучения модели с какими-то конкретными гиперпараметрами **мы узнаем, какое именно значение принял оптимизируемый функционал. На основе этой информации мы строим свою аппроксимацию распределения (называемого апостериорным), которое мы уточняем на каждом шаге и из которого семплируем значения гиперпараметров.
Апостериорное распределение, как правило, задаётся параметрически, и оптимизируются именно его параметры (да, в машинном обучении оптимизация параметров распределения гиперпараметров модели — обычный вторник).
В конечном итоге каждый шаг подбора гиперпараметров дороже с вычислительной точки зрения, но суммарное число попыток уменьшается в разы.
Если коротко подытожить, то в поиске по сетке и случайном поиске мы никак не используем информацию об уже «проверенных» значениях гиперпараметров, а в байесовской оптимизации мы опираемся на результаты уже проведённых экспериментов и рассматриваем ту часть пространства гиперпараметров, в которой вероятность получить лучший результат наивысшая.
Под капотом библиотеки optuna — комбинаторика и умный поиск
Идеи байесовского выбора новых точек хорошо работают на практике, но современные инструменты идут дальше.
Библиотека optuna сочетает вероятностный отбор со структурированием комбинаторного пространства и распределением бюджета экспериментов, что позволяет резко сократить число запусков без потери качества.
По сути, происходят две вещи: пространство поиска делают более «умным», а слабые варианты отсекают как можно раньше. Давайте посмотрим, как именно этого добиваются.
Сначала про структуру. Простейший способ оценить пространство поиска — перемножить число вариантов для каждого гиперпараметра, как мы делали в переборе по сетке выше. Но в реальных задачах всё сложнее: многие гиперпараметры условны и включаются только при определённом выборе других.
Это кардинально меняет математику подсчёта. Вместо одного большого декартова произведения мы получаем несколько независимых «ветвей» поиска. Общее число комбинаций тогда считается не по правилу произведения, а по правилу суммы — мы складываем размеры пространств для каждой ветки.
Более формально вместо мы получаем
где — ветка (набор согласованных выборов), — активные на ней параметры.
Рассмотрим довольно классический пример с SVM. Пусть у нас есть параметры:
- Ядро
kernel. - Коэффициент регуляризации
C(4 варианта). - Коэффициент ядра
gamma(4 варианта, только дляrbf). - Степень полинома degree (3 варианта, только для
poly).
Наивный подсчёт дал бы нам комбинации, большинство из которых недопустимы (например, kernel='linear' и degree=3). А правильный способ здесь — это именно сумма по веткам:
Всего 32 допустимые комбинации вместо 144. Этот простой подсчёт показывает, как учёт структуры задачи комбинаторно сжимает пространство поиска.
💡Если есть запрещённые сочетания (допустим, нельзя брать A и D вместе) или взаимоисключающие группы, их удобно учитывать правилом произведения и методом включений-исключений: вычитаем запрещённые подпространства и корректируем пересечения.
Теперь про экономию бюджета. Тратить ресурсы на обучение заведомо слабых конфигураций — непозволительная роскошь. Для борьбы с этим optuna использует pruning (отсечение), который работает по принципу турнира на выживание (алгоритм Successive Halving).
Представьте, что у нас есть 100 конфигураций гиперпараметров — это наши участники турнира на выживание:
- Раунд 1. Мы даём всем 100 участникам минимальный бюджет (например, обучаем всего одну эпоху) и оцениваем их результат.
- Раунд 2. Мы отбрасываем половину худших, а оставшимся 50 «выжившим» даём удвоенный бюджет (еще несколько эпох).
- Раунд 3. Снова отбрасываем половину и удваиваем бюджет для оставшихся 25.
И так далее. До финала (полного бюджета на обучение) доходят лишь несколько самых сильных конфигураций. Интуиция простая: лучше немного потратить на многих и быстро понять, кто перспективен, чем одинаково дорого обучать всех. С точки зрения комбинаторики это буквально отсечение целых ветвей в большом дереве возможных решений.
Наконец, откуда берутся новые кандидаты. Вместо того чтобы пробовать точки вслепую, optuna использует алгоритм TPE (англ. Tree-structured Parzen Estimator), который работает как опытный рыболов. Он делит уже просмотренные точки на удачные (скажем, верхние 25% по метрике, этот порог задаётся параметром ) и остальные, строит для каждой группы свою вероятностную модель и выбирает новые точки там, где хороший улов встречается чаще, а плохой — реже.
Формально мы получаем две функции плотности:
- — это распределение значений гиперпараметров , характерное для «удачных» результатов.
- — распределение, характерное для «неудачных» результатов.
Следующий кандидат для проверки выбирается из области, где вероятность получить хороший результат высока, а плохой — низка. Математически это означает, что TPE ищет точку , которая максимизирует отношение .
Таким образом, вместо равномерного обхода всего декартова произведения поиск разумно концентрируется на наиболее перспективных областях.
Вместе эти приёмы не отменяют рост пространства решений, но позволяют обращаться с ним бережно: учитывать структуру, быстро зачищать слабые ветви и направлять попытки туда, где это имеет смысл.
А теперь поговорим о том, почему вообще это пространство так быстро разрастается и к каким эффектам это приводит.
Проклятие размерности и комбинаторный взрыв
В мире машинного обучения достаточно часто упоминают т. н. «проклятие размерности», но далеко не всегда приводится понятное объяснение, в чём же оно заключается.
Термин «проклятие размерности» принадлежит Ричарду Беллману (1920–1984), американскому математику и основателю динамического программирования. Его мысль была простой: рост размерности сам по себе делает многие наивные методы непрактичными, но это не повод сдаваться.
«И хотя это „проклятие“ уже много лет висит над физиками и астрономами, не стоит отчаиваться: значимые результаты можно получить несмотря на него».
“Since this is a curse which has hung over the head of the physicist and astronomer for many a year, there is no need to feel discouraged about the possibility of obtaining significant results despite it”.
Чтобы не быть голословными, проиллюстрируем эту мысль Беллмана на упрощённом (и несколько теоретизированном) примере из замечательной книжки «Геометрическое глубокое обучение: решётки, группы, графы, геодезические и калибры».
Для этого нам придётся ввести определение функции, непрерывной по Липшицу: функция называется непрерывной по Липшицу, если существует такая константа , что для любых двух точек из области определения функции верно следующее выражение:
По сути мы утверждаем, что абсолютное значение производной (а значит, и скорости роста) функции ограничено сверху числом , и функция меняется достаточно плавно.
Зачем нам это определение? Мы сейчас построим очень послушную (гладкую) функцию, которая тем не менее потребует экспоненциально много наблюдений. Липшицевость зафиксирует именно эту «послушность».
Теперь перейдём к проклятию размерности. Для его иллюстрации нам понадобится понятие -мерного единичного гиперкуба — здесь мы понимаем множество . Проще всего представить его так:
- При это отрезок с двумя вершинами-концами: .
- При это квадрат с четырьмя вершинами: .
- При это куб с восемью вершинами.
Интуитивная картинка очень простая: представьте, что у нас есть независимых переключателей . Каждая возможная конфигурация этих переключателей — это одна из вершин гиперкуба. По правилу произведения, общее число таких конфигураций (а значит, и вершин) равно . Формально множество вершин — это , а сам гиперкуб — это всё пространство внутри них, то есть множество точек .
Рассмотрим теперь липшицеву функцию вида
где , расположены в вершинах гиперкуба, а – липшицева функция с константой , похожая, например, на гауссиану. Здесь липшицева, значит и вся сумма липшицева; знак задаёт «вверх» или «вниз» в окрестности вершины .
Поскольку знаки независимы, без наблюдения в вершине мы не узнаем, куда «загибается» функция именно там. Следовательно, чтобы корректно её аппроксимировать на всём гиперкубе, нужно минимум наблюдений — по одному на вершину.
Мы видим, что их число растёт экспоненциально с ростом размерности пространства, что недопустимо в задачах машинного обучения: в современных задачах размерность пространства может достигать десятков и сотен тысяч (а может быть, и больше).
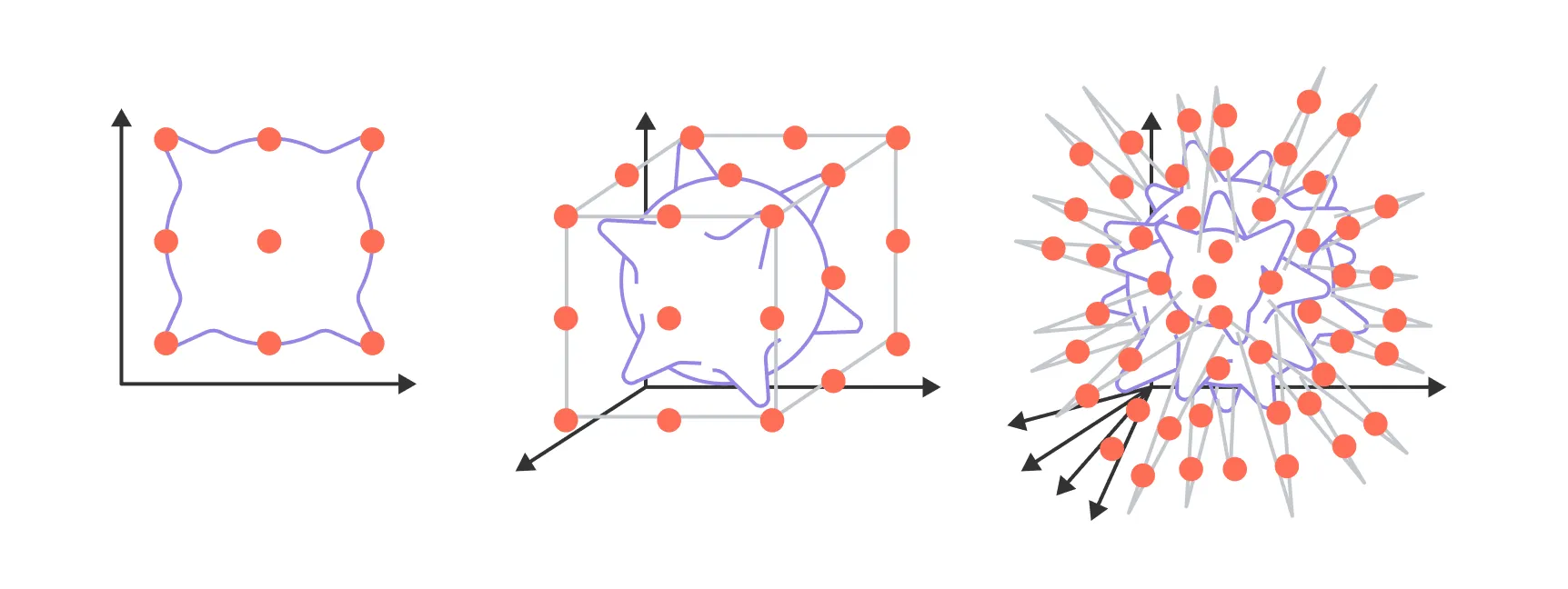
По сути, мы наблюдаем тот же комбинаторный взрыв, но уже в непрерывном представлении: чем больше размерность пространства, тем больше нам нужно примеров для обучения.
Если бы мы не пользовались дополнительной информацией о решаемой задаче, будь то физические ограничения, экспертные знания или симметрия данных, то решение сложных задач было бы для нас недоступным.
Чтобы было понятно, в какой задаче возникает проклятие, представим обычный процесс обучения: мы хотим построить классификатор , который по входу предсказывает класс. Если не накладывать дополнительных структурных предположений о данных или о самой (кроме общей плавности), то для надёжного обобщения нужно покрыть область достаточным числом примеров, а необходимое число таких точек растёт экспоненциально по размерности . На конкретном примере это видно особенно ясно.
Даже для классификации простой картинки размерами (как в наборе данных CIFAR) необходимо работать с пространством размерностью (пусть изображение приведено в чёрно-белую палитру). Даже если каждый пиксель принимает лишь значения или (т. е. по сути является бинарным), формально различных вариантов уже , и рассмотреть их все нет никакой физической возможности.
Именно поэтому во всех современных подходах в области глубокого обучения используются модели, которые учитывают симметрии данных. Например, операция свёртки эквивариантна к сдвигу, механизм внимания (англ. self-attention) — к перемешиванию и пр.
В этом параграфе мы разобрали, что гиперпараметры задают форму модели и почему их подбор дорог: каждый новый переключатель комбинаторно раздувает число конфигураций.
Сравнили три базовые стратегии: сетку, случайный поиск и байесовскую оптимизацию — и увидели, как практические инструменты вроде optuna структурируют пространство (условные ветки), экономят бюджет за счёт досрочного отсечения слабых конфигураций и направляют попытки туда, где есть шанс на выигрыш.
Наконец, мы ввели интуицию проклятия размерности: без дополнительных предположений объём данных, нужных для надёжного обучения в высоких размерностях, растёт экспоненциально. На практике нас выручают структура, симметрии и явные ограничения.
В мире машинного обучения комбинаторика обычно не даёт ответов на вопрос «как решать эту задачу?». Вместо этого она позволяет оценить сложность задачи, натолкнуть на мысли о поиске дополнительных ограничений и в целом оптимизировать трудозатраты. Многие из упомянутых подходов и тем ещё не раз встретятся вам в следующих главах и в реальных задачах.
В заключительном параграфе мы соберём ключевые идеи всей главы в одном месте — от языка множеств и правил подсчёта до метода включений-исключений. И зафиксируем, каким набором приёмов вы теперь владеете.




