Мы уже познакомились с основными понятиями из мира комбинаторики, с правилами суммы и произведения, а также с классическими формулами для размещений и сочетаний.

Наш следующий шаг — научиться аккуратно считать объединения пересекающихся множеств и упорядочивать пространство всех подмножеств. Эти инструменты пригодятся, когда условий и объектов много и легко допустить двойной счёт.

По дороге увидим, как эти идеи напрямую работают в задачах анализа данных и машинного обучения.

В этом параграфе вы узнаете:

• Метод включений-исключений: как считать мощность объединений пересекающихся множеств и вывести общую формулу.
• Множество всех подмножеств: что такое power set, почему его размер равен и как это связано с отбором признаков.

Но перед тем как мы продолжим, вот вам задачка:

Оцените, во сколько раз увеличится число возможных паролей длины 8 из букв латинского алфавита (26 букв) в нижнем регистре и цифр от 0 до 9, если помимо строчных букв могут использоваться и заглавные.

Ответ (не открывайте сразу; сперва подумайте сами!)

Общее число уникальных символов изначально составляло . Символы могут повторяться в пароле, т. е. общее число возможных паролей составляло

Если же мы будем использовать также буквы верхнего регистра, общее число символов станет равным . Следовательно, уникальных паролей теперь , и их количество увеличилось в раз.

Метод включений-исключений

Для начала рассмотрим один из центральных методов работы с множествами (или их подмножествами) сложной структуры.

Говоря формально, он позволяет найти мощность объединения конечного числа конечных множеств, которые могут пересекаться между собой. Говоря проще, он позволяет избежать многократного учёта элементов, которые сразу принадлежат нескольким множествам.

Например, если мы хотим найти мощность объединения множеств и , то мы не можем просто сложить их мощности, т. к. пересечение будет учтено дважды — его нужно исключить. Т. е. для случая двух множеств

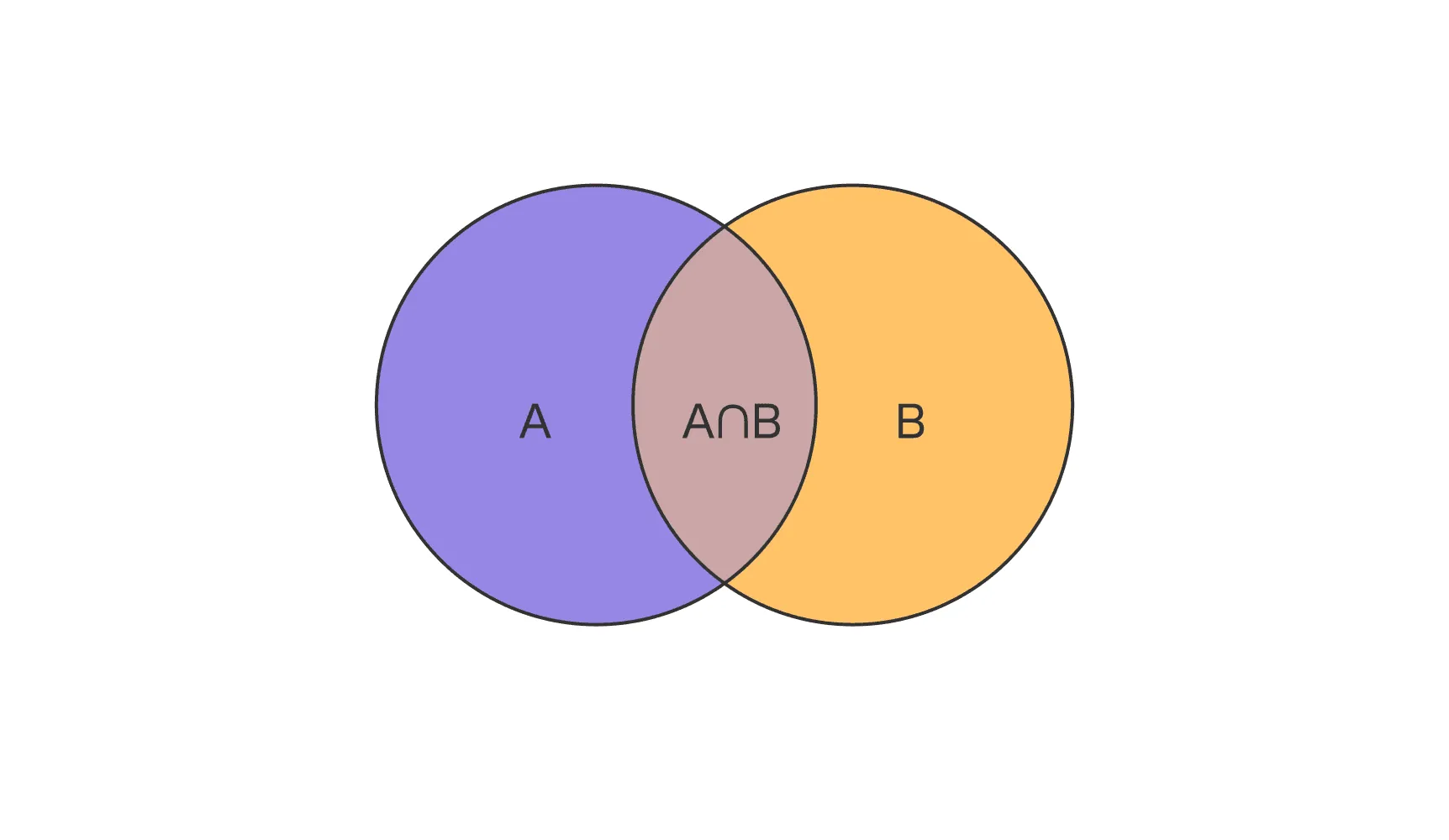
Но что делать, если этих множеств больше? Сначала разберемся с тремя множествами на живом примере.

Пример: три пересекающихся множества

В ШАД (Школе Анализа Данных Яндекса) читается множество курсов. Для простоты будем считать, что в первом семестре читаются три курса: алгоритмы , машинное обучение и разработка на Python — и у нас есть список всех студентов каждого из курсов. Если сложить численность студентов каждого курса, мы наверняка посчитаем кого-то дважды или трижды — люди ходят сразу на несколько курсов. Используя метод включений-исключений, мы сможем найти общее число студентов.

Сложим мощности , и , тогда студенты, принадлежащие их пересечениям, будут учтены дважды. Значит, исключим мощности пересечений — тех, кто ходит одновременно на два курса: , и . Но если студент записан на все три курса, то мы его проигнорировали (три раза учли, три раза исключили). Значит, всех таких студентов нужно учесть явным образом, т. е. добавить мощность множества . В конечном итоге получается формула:

Пример на числах

Пусть на трёх курсах у нас такие данные:
;
;
.
Тогда по формуле включений-исключений:

Итого: на трёх курсах обучаются 175 уникальных студентов.

💡Примечание: внимательный читатель заметит, что технически найти мощность объединения можно было бы напрямую, объединив все множества и посчитав итоговый размер. В Python, например, это делается буквально одной строчкой: len(A.union(B).union(C)).

Это верное замечание, но далеко не всегда нам удобно оперировать элементами множеств в явном виде. В одном из примеров далее мы это проиллюстрируем.

Ещё более внимательный читатель заметит некоторую регулярность: мы учитываем мощности самих множеств, вычитаем мощность пересечений пар, добавляем мощность пересечений троек... А что, если множеств не три, а некоторое число ? Именно на этот вопрос и отвечает формула включений-исключений в общем виде.

Формула включений-исключений

Для конечных множеств верно

Геометрически данный результат выглядит достаточно очевидным. Ниже в качестве иллюстрации приведена диаграмма Эйлера — Венна для трёх множеств: алфавитов греческого, русского и латинского языков.

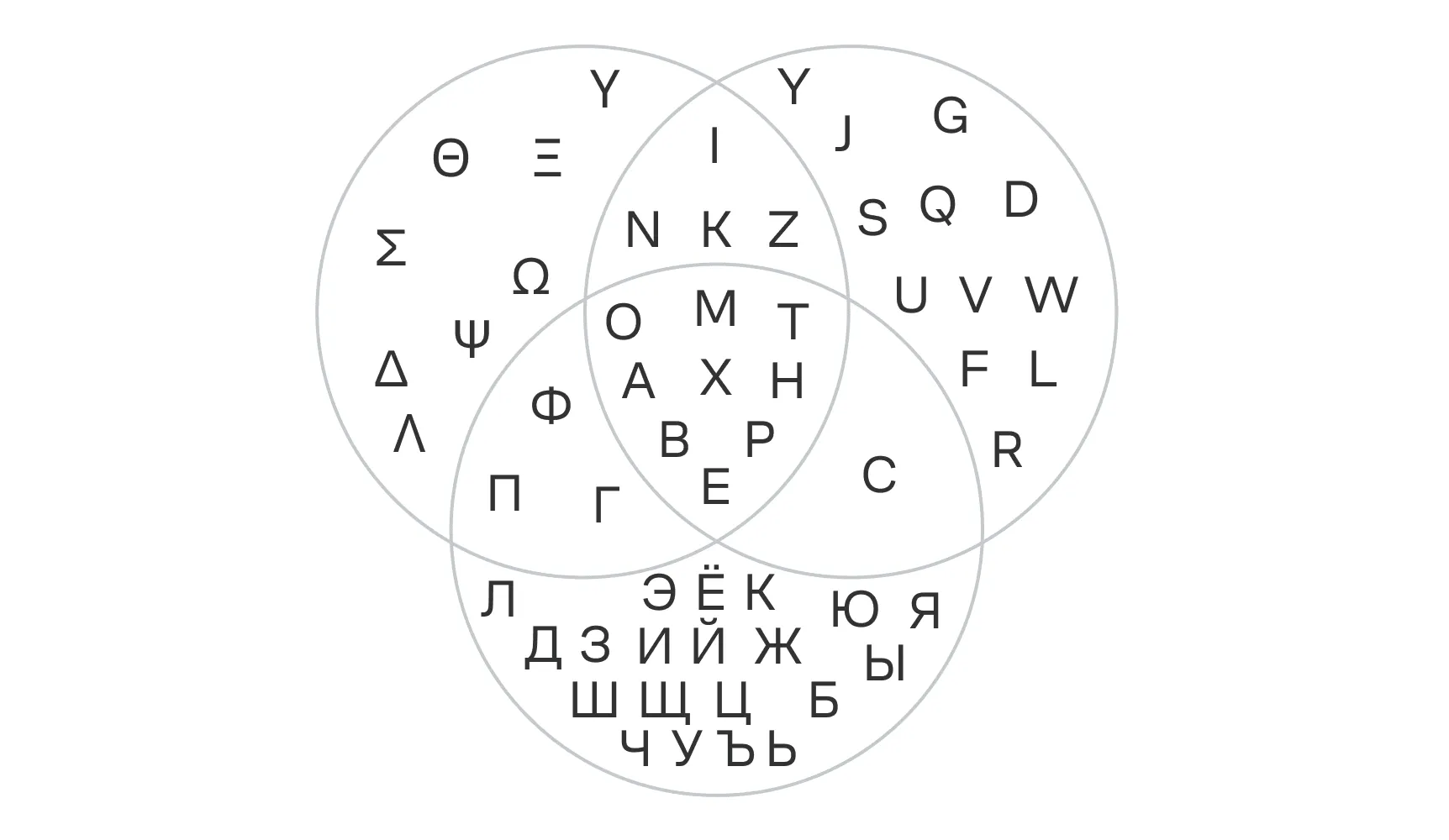
Чуть более комбинаторный пример

Рассмотрим задачу: сколькими способами можно выбрать число от 1 до 120, которое не делится ни на 2, ни на 3, ни на 5?

Обозначим множества:

,
,
,
.

Мощности этих множеств легко посчитать — это результат целочисленного деления общего числа элементов на соответственное число:

где обозначает число, округлённое вниз.

Аналогичным образом , .

Тогда мы также легко найдём количество чисел, которые делятся на 2 и на 3: .

Аналогично для 2 и 5: , и для 3 и 5: .

Для всех трёх чисел: .

Мы знаем количество чисел не превышающих 120, которые делятся на 2, 3 или 5, обозначим это число за . Т. к. числа могут либо делиться, либо не делиться на заданные, количество чисел, которые на 2, 3 или 5 не делятся, есть .

В конечном итоге:

Итого: от 1 до 120 всего 32 числа не делятся ни на 2, ни на 3, ни на 5.

Задание. Докажите, что в формуле включений-исключений для множеств ровно слагаемых.

Ответ (не открывайте сразу; сперва подумайте сами!)

К решению данной задачи можно подойти по-разному. Мы приведём лишь одно из возможных решений.

Рассмотрим формулу включений-исключений. Если доступных множеств , то в формуле мы получим:

• слагаемых от одиночных множеств
• слагаемых от пересечений пар множеств
• слагаемых от пересечений троек множеств
• слагаемое от пересечения всех множеств

Т. е. общее число слагаемых есть сумма:

В предыдущем параграфе мы разбирали треугольник Паскаля. В нём все элементы в каждой строке — это число сочетаний , где есть номер строки, а — номер элемента (но считая с нуля!). Пользуясь свойством биномиальных коэффициентов, а именно:

Обратим внимание, что суммы практически совпадают. Если положить , получим:

Осталось лишь вычесть единицу (), т. к. суммирование идёт не с , а с .

Множество всех подмножеств

Зачастую при работе с множествами возникает необходимости оценить количество всех возможных подмножеств. Например, при выборе оптимального набора признаков, что мы рассмотрим в дальнейшем.

Введем формальное определение:

Для конечного множества множество всех его подмножеств обозначается как , и его мощность (т. е. количество всех возможных подмножеств) равна . В англоязычной литературе оно часто обозначается как power set или powerset.

Стоит отметить, что множество всех подмножеств включает и пустое множество , и само множество .

Доказательство

Давайте формально покажем, что множество всех подмножеств состоит ровно из элементов.

Пронумеруем все элементы множества и сопоставим каждому элементу 1 бит — бинарную величину. Тогда любому подмножеству соответствует одна из строк длиной вида

000111010011...000

где на позиции соответствует включению -го элемента в множество, а — невключению.

Всего возможных строк такого вида будет ровно , причём строка из одних нулей соответствует пустому множеству , а из одних единиц — множеству .

Пример из практики — аугментации изображений

Когда обучают модель распознавать картинки, исходных фотографий часто мало. Чтобы не кормить модель одними и теми же кадрами, делают простые преобразования исходных изображений — аугментации.

Это вроде мелких искажений, которые не меняют смысл картинки (кот остаётся котом), но дают модели больше разнообразия: отразили по горизонтали, слегка повернули, чуть обрезали края, поменяли яркость/контраст, добавили немного шума.

Представьте, что у нас есть 5 независимых аугментаций:

1. Горизонтальный флип (зеркальное отражение кадра относительно вертикальной оси).
2. Небольшой поворот.
3. Случайный кроп (обрезка).
4. Изменение яркости/контраста.
5. Добавление шума.

Любая такая схема аугментаций — это буквально подмножество из этих пяти операций: какие-то включили, какие-то нет.

Значит, общее число схем — как раз мощность множества всех подмножеств: .

Для наглядности несколько вариантов из этих :

• - ничего не делать (исходное изображение);
• ;
• ;
• ;
• ;
• ;
• — все пять.

Каждая строка — это один набор флажков, и ровно такой набор соответствует одному подмножеству исходного множества аугментаций. Отсюда и формула : у каждой из операций два состояния — .

Примечание. В реальных системах порядок и сила аугментаций тоже имеют значение (например, повернуть на 5° или на 10°). Тогда пространство вариантов растет ещё быстрее. Но базовая идея с подсчётом отлично иллюстрирует именно «включение/выключение» операций как множества подмножеств.

Именно здесь комбинаторика проявляется в ML: когда выбор раскладывается на независимые бинарные решения, число конфигураций равно . Если у переключателя больше двух режимов, общее число вариантов — произведение мощностей соответствующих множеств. Давайте посмотрим на другой очень значительный пример из машинного обучения.

Отбор признаков в машинном обучении

В машинном обучении для получения точного, простого и интерпретируемого решения крайне важно иметь качественное признаковое описание для всех объектов. Но не все признаки одинаково полезны: многие из них могут дублировать друг друга (т. е. признаковое описание может являться избыточным) или же вовсе быть бесполезными. Поэтому часто необходимо оставить лишь наиболее значимые признаки, т. е. возникает задача отбора признаков.

Пусть нам доступна выборка, где каждый объект описывается 20 признаками. Полный перебор всех комбинаций означает проверку

подмножеств — и на каждом подмножестве нужно обучить модель, не забыть про валидационную выборку, а то и провести кросс-валидацию. Очевидно, что даже с современными вычислительными ресурсами эта задача нетривиальна.

💡А ведь признаков может быть гораздо больше, в реальных задачах их десятки, сотни или даже сотни тысяч.

Более того, добавление одного нового признака моментально удваивает количество усилий — теперь каждое изначальное подмножество либо включает его, либо нет. Поэтому на практике, ввиду экспоненциального роста сложности, полный перебор практически никогда не применяется.

К наиболее широко известным методам отбора признаков относятся:

• жадный перебор;
• методы, которые опираются на использование уже обученной модели (например, SHAP);
• некоторые методы регуляризации, например -регуляризация «отбирает» признаки путём зануления их весовых коэффициентов;
• случайный поиск (особенно если признаков много и потеря некоторых из них не является критичной);
• байесовская оптимизация и другие методы.

Примечание: ещё раз обратим внимание на интуитивно понятную иллюстрацию количества всех возможных подмножеств: в случае признаков каждый признак могут либо взять, либо нет, т. е. общее число комбинаций и будет .

Вопрос. Сколькими способами можно выбрать ровно 5 признаков из 12?

Ответ (не открывайте сразу; сперва подумайте сами!)

Достаточно воспользоваться формулой сочетаний из предыдущей главы: .

---

Итак, в этом параграфе мы научились аккуратно считать мощности объединений пересекающихся множеств: от наглядных диаграмм Венна до общей формулы включений-исключений для произвольного числа множеств.

Мы увидели, как эта техника помогает отвечать на вопросы о том, сколько объектов не подпадает ни под одно из ограничений, а также познакомились со множеством всех подмножеств и поняли, почему его размер равен в степени мощности исходного множества. Эти идеи уже прямо работают в практических задачах — например, при оценке пространства вариантов в отборе признаков.

Дальше перенесём этот инструментарий в машинное обучение: посмотрим, как считать и сравнивать размеры пространств гиперпараметров, чем отличаются сеточный и случайный поиск, зачем нужна байесовская оптимизация и как всё это связано с проклятием размерности.