В предыдущем параграфе мы познакомились с тем, что такое факторный анализ, и как его проводить в теории. В этой научимся проводить его с помощью Python — в качестве датасета будем использовать набор данных с характеристиками, которые могут быть связаны с сахарным диабетом. Скачайте его и положите в папку с проектом.
Подготовка данных
Начнем с того, что загрузим нужные нам библиотеки, методы и сам набор данных. Как всегда, нам понадобится pandas, кроме того из библиотеки statsmodels мы загрузим методы для реализации факторного анализа.
Если у вас не установлена библиотека statsmodels, то установить её можно так же, как и все другие библиотеки.
Наконец, мы загрузили наш набор данных и вывели список переменных с помощью метода columns, которые в нем содержатся.
1import pandas as pd
2from statsmodels.multivariate.factor import Factor
3df = pd.read_csv('diabetes_012_health_indicators_BRFSS2015.csv')
4df.columns
1Index(['Diabetes_012', 'HighBP', 'HighChol', 'CholCheck', 'BMI', 'Smoker',
2 'Stroke', 'HeartDiseaseorAttack', 'PhysActivity', 'Fruits', 'Veggies',
3 'HvyAlcoholConsump', 'AnyHealthcare', 'NoDocbcCost', 'GenHlth',
4 'MentHlth', 'PhysHlth', 'DiffWalk', 'Sex', 'Age', 'Education',
5 'Income'],
6 dtype='object')
Подробное описание переменных доступно по ссылке.
Мы видим, что тут есть переменная с информацией о наличии или отсутствии у индивида сахарного диабета. Все оставшиеся переменные — это его индивидуальные характеристики, предположительно связанные с возникновением сахарного диабета. Если мы захотим провести T-test или любой другой из тех, что мы обсуждали или ещё обсудим, то довольно сложно провести его для каждой из 22 переменных.
Ещё можно попробовать увидеть за переменными объёмную картину: как они связаны между собой. 22 переменных неизбежно как-то связаны между собой, мы можем попробовать выделить из них факторы. Если благодаря этому мы сможем преобразовать 22 переменные в три или четыре, то мы сможем дальше использовать их в анализе.
Но прежде чем мы пойдем дальше, взглянем на размер датафрейма. Это может быть важным — ниже мы объясним, почему.
1df.shape
1(253680, 22)
Как видите, наблюдений у нас очень много. Из-за этого обработка данных может быть долгой. Факторный анализ требует множества вычислений, поэтому работа с полными данными может быть довольно медленной. Решение простое — сделать случайную выборку из данных: например, взять всего 1000 наблюдений.
Вообще, это хороший способ упросить себе жизнь, когда вы пишете код. Вместо того чтобы использовать полный набор данных, можно сделать относительно маленькую выборку. Так окажется, что код, корректность которого вам нужно проверить, запускается быстрее, чем с полным набором данных. Это экономит ваше время. Главное, не забыть в конце провести все расчеты на полной версии данных.
1df_sample = df.sample(1000)
Выберем необходимые колонки. Фактически, мы исключили одну единственную: независимую переменную Diabetes_012.
1df_sample = df_sample[['HighBP', 'HighChol', 'CholCheck', 'BMI', 'Smoker',
2 'Stroke', 'HeartDiseaseorAttack', 'PhysActivity', 'Fruits', 'Veggies',
3 'HvyAlcoholConsump', 'AnyHealthcare', 'NoDocbcCost', 'GenHlth',
4 'MentHlth', 'PhysHlth', 'DiffWalk', 'Sex', 'Age', 'Education',
5 'Income']]
Это те колонки, с которыми мы будем работать. Посмотрим на них повнимательнее.
1print(df_sample.describe())
1 HighBP HighChol CholCheck BMI Smoker Stroke HeartDiseaseorAttack
20 1.0 1.0 1.0 40.0 1.0 0.0 0.0 \
31 0.0 0.0 0.0 25.0 1.0 0.0 0.0
42 1.0 1.0 1.0 28.0 0.0 0.0 0.0
53 1.0 0.0 1.0 27.0 0.0 0.0 0.0
64 1.0 1.0 1.0 24.0 0.0 0.0 0.0
7
8 PhysActivity Fruits Veggies ... AnyHealthcare NoDocbcCost GenHlth
90 0.0 0.0 1.0 ... 1.0 0.0 5.0 \
101 1.0 0.0 0.0 ... 0.0 1.0 3.0
112 0.0 1.0 0.0 ... 1.0 1.0 5.0
123 1.0 1.0 1.0 ... 1.0 0.0 2.0
134 1.0 1.0 1.0 ... 1.0 0.0 2.0
14
15 MentHlth PhysHlth DiffWalk Sex Age Education Income
160 18.0 15.0 1.0 0.0 9.0 4.0 3.0
171 0.0 0.0 0.0 0.0 7.0 6.0 1.0
182 30.0 30.0 1.0 0.0 9.0 4.0 8.0
193 0.0 0.0 0.0 0.0 11.0 3.0 6.0
204 3.0 0.0 0.0 0.0 11.0 5.0 4.0
21
22[5 rows x 21 columns]
Обратите внимание, что у разных переменных разные шкалы. В прошлом параграфе мы обсуждали, что это может снизить точность результатов факторного анализа. Поэтому нам нужно привести переменные к стандартизированным значениям. Так как формула преобразования довольно простая, то мы можем просто вычислить её для каждой переменной.
1for col in df.columns:
2 df[col] = (df[col] - df[col].mean()) / df[col].std()
Обратите внимание, что мы совершили преобразование над каждой колонкой по отдельности в цикле. Для этого мы получили список всех колонок с помощью метода df.columns, а дальше подставляли каждую из них по очереди в цикле. Вычисления в данном случае не отличаются от любого другого изменения переменной. После этого все наши переменные находятся на одной шкале и сравнимы друг с другом. В будущем мы неоднократно будем применять этот алгоритм, так что обратите на него внимание. Давайте воспользуемся готовыми переменными и приступим к факторному анализу!
Факторный анализ
Начнём с того, что вычислим связь между переменными и факторами для случайного числа факторов. Допустим, мы возьмем три. Мы начинаем с полностью случайного выбора числа факторов, чтобы потом уточнить и прийти к наилучшему варианту.
Для этого мы используем уже загруженный нами ранее метод Factor. В качестве аргументов мы указываем наш датафрейм, желаемое число факторов и метод, который мы будем использовать. В данном случае pa соответствует методу главных компонент.
Само преобразование делается в два шага. Сначала мы «создаём» модель с желаемыми параметрами и сохраняем её как переменную, а затем используем метод fit() и вычисляем результат преобразований.
Это тоже часто используемая схема, с которой вы столкнетесь в дальнейшем неоднократно. Сначала создаем объект с желаемыми параметрами, потом сводим их вместе.
1fa = Factor(df, n_factor=3, method='pa')
2res = fa.fit()
Давайте теперь поймем, что именно мы получили. Начнем с того, что посмотрим на таблицу факторных нагрузок. Она отражает корреляцию между фактором и переменной. Подсветим все значения больше 0.3 и меньше -0.3. Их мы будем считать достаточными.
1res.get_loadings_frame(threshold=0.3)

Мы видим в таблице какой-то первоначальный вариант группировки. Выделенные вместе переменные относятся к одному фактору, указанному в столбце. Мы можем попробовать интерпретировать их. Проще всего начать с третьего, который соответствует вопросам о наличии в рационе овощей и фруктов. Мы могли бы объединить его и сказать, что это скрытый фактор — «Питание».
Мы видим, что это очень-очень слабый фактор (все значения не укладываются в диапазон -0.3—0.3). Кроме того, он связан с полом, образованием и физическим здоровьем: интуитивно кажется, что все эти вопросы связаны с питанием.
Со вторым сложнее. Там есть вопросы о возрасте, уровне холестерина и два вопроса о доступности медицинской помощи. Мы можем предположить, что это возрастные изменения: холестерин повышается с возрастом, доступность медицинской помощи становится более важной с течением возраста. Давайте пока предположим, что этот фактор можно объединить и связать с «возрастными изменениями».
Наконец, factor0 — состоит из наибольшего числа переменных. Большая часть из них связана с разными формами здоровья, дохода и уровня образования. Все вместе это можно объединить и назвать «Уровень жизни».
Итого, у нас получилось три фактора: уровень жизни, возрастные изменения и питание. И мы могли бы удовлетвориться этим результатом, однако у нас нет уверенности, что именно такое число факторов будет подходящим. factor2 выглядит не очень надежно.
А что будет, если бы мы взяли не три фактора, а два или четыре? Мы говорили, что мы можем использовать метод локтя для проверки. Давайте посмотрим на это.
Выбор числа факторов
Как вы помните, метод локтя — это график, который мы оцениваем визуально. Чтобы его получить, нужно выполнить следующий код. Нам понадобится пакет matplotlib, так как без него нельзя создать график. Дальше мы используем метод plot_scree(), который применяем к переменной res с результатами прошлых вычислений.
1import matplotlib.pyplot as plt
2res.plot_scree()
3plt.show()

Однозначно можно сказать, что первые два фактора будут наиболее полезны — на них приходится наибольшая доля объяснённой дисперсии. Мы видим это, глядя на точку перегиба. Давайте попробуем оценить более строгий вариант с двумя факторами.
Факторный анализ альтернативного варианта
Содержательно, наш код совсем не изменится за исключением единственного числа: количества факторов.
1fa = Factor(df, n_factor=2, method='pa')
2res = fa.fit()
3res.get_loadings_frame(threshold=0.3)
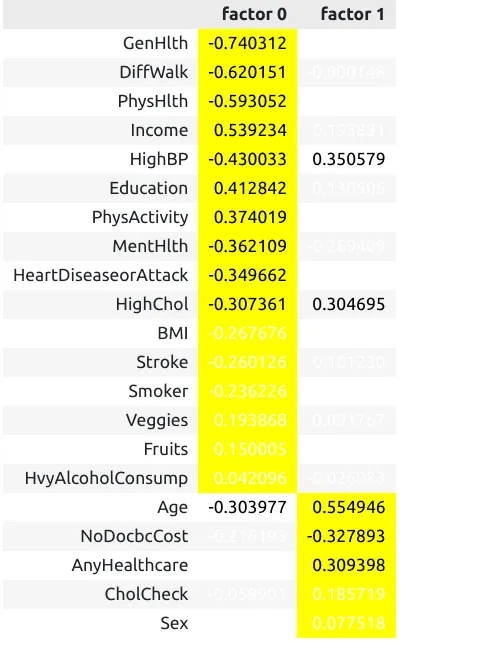
Мы видим, что фактически, сохраняются два первых фактора, которые мы условно назвали «уровень жизни» и «возрастные изменения». Кажется, что это наилучшая комбинация.
В итоге мы можем сделать следующий вывод: факторы, потенциально связанные с сахарным диабетом могут быть объединены в две группы. Одни касаются уровня жизни, другие возрастных изменений.
Обратите внимание, что мы не говорим о том, что какой-то из двух факторов связан с сахарным диабетом. Для этого мы могли бы использовать другие методы анализа данных.
Например, мы могли бы вычислить значения факторов, а потом разделить их на две группы (есть сахарных диабет или нет) и провести, например, T-test. В одном из следующих параграфов мы поговорим про регрессионный анализ, который тоже может быть использовать вместе с факторным анализом.
Сам по себе факторный анализ — это метод, который с одной стороны может использовать для получения содержательных интерпретаций, а с другой — как вспомогательный шаг при дальнейшем моделировании.
В следующем разделе мы поговорим о том, как собирать открытые данные из любого публичного источника в интернете — и правильно их описывать для других исследователей.


