Метод опорных векторов (англ. Support Vector Machine, SVM) — это один из ключевых алгоритмов классификации, сочетающий строгое геометрическое обоснование с хорошими обобщающими свойствами.
В отличие от логистической регрессии, которая минимизирует логарифмическую функцию потерь, SVM стремится построить решающую границу с максимальным зазором (margin) между классами. При этом он сохраняет линейную структуру модели, а при необходимости легко обобщается на нелинейные зависимости через так называемый ядровой трюк.
В этом параграфе:
- Мы начнём с постановки задачи SVM в геометрической форме и разберём, как ширина зазора связана с нормой вектора весов.
- Затем последовательно перейдём к двойственной формулировке, где всё выражается через скалярные произведения и матрицу Грама, и на этом фоне станет понятен принцип ядрового трюка.
- В завершении обсудим, как понятие VC-размерности помогает оценить обобщающую способность SVM.
Поехали!
Постановка задачи классификации и её решение
Пусть даны обучающие данные , где — векторы признаков, а — бинарные метки классов. SVM ищет разделяющую гиперплоскость вида:
где:
- — вектор нормали к гиперплоскости;
- — смещение.
На графике ниже показана гиперплоскость и её нормаль . Вектор перпендикулярен разделяющей границе и определяет направление, вдоль которого производится классификация.
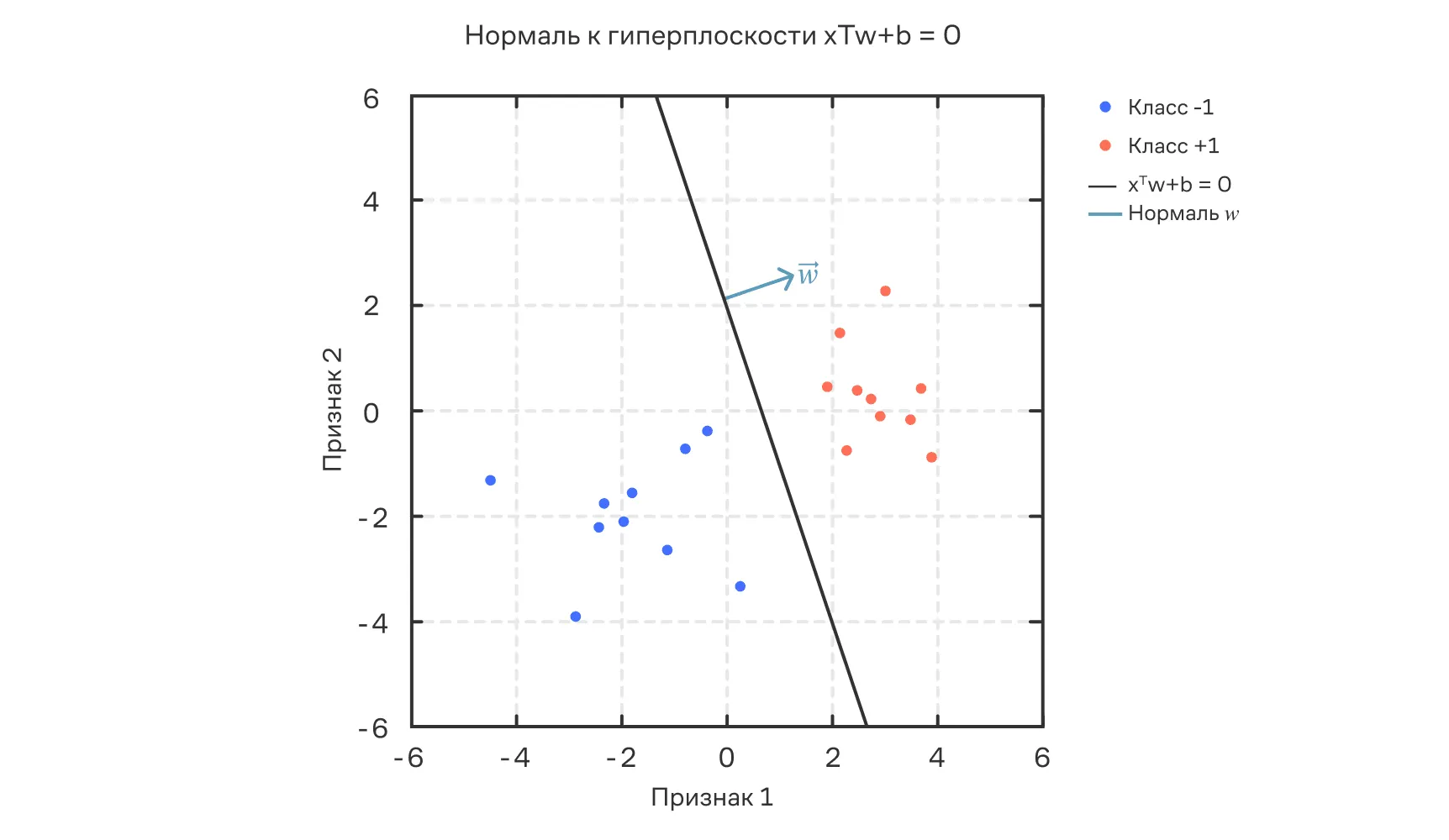
Разделяющая гиперплоскость и её нормаль .
Предсказанный класс для объекта определяется знаком скалярного выражения:
Если результат положителен, объект классифицируется как принадлежащий классу ; если отрицателен — классу .
Цель алгоритма SVM — подобрать такие и , чтобы предсказания совпадали с истинными метками.
Чтобы модель правильно классифицировала объект с меткой , необходимо, чтобы знак предсказания совпадал со знаком истинной метки. Это можно выразить одним условием:
Это условие эквивалентно правильной классификации:
- Если , нужно, чтобы , иначе условие выполнено не будет.
- Если , нужно, чтобы , иначе условие выполнено не будет.
Таким образом, выражение означает, что объект классифицирован правильно, а знак ответа модели согласован с истинным классом.
Это — основа всей геометрии линейного классификатора.
Однако условие допускает бесконечно много решений: если удовлетворяют неравенствам, то и при любом тоже.
Ниже на графике представлено несколько примеров допустимых гиперплоскостей без нормировки. Все разделяют классы правильно, но проходят по-разному. Чтобы выбрать единственную, необходимо зафиксировать масштаб.
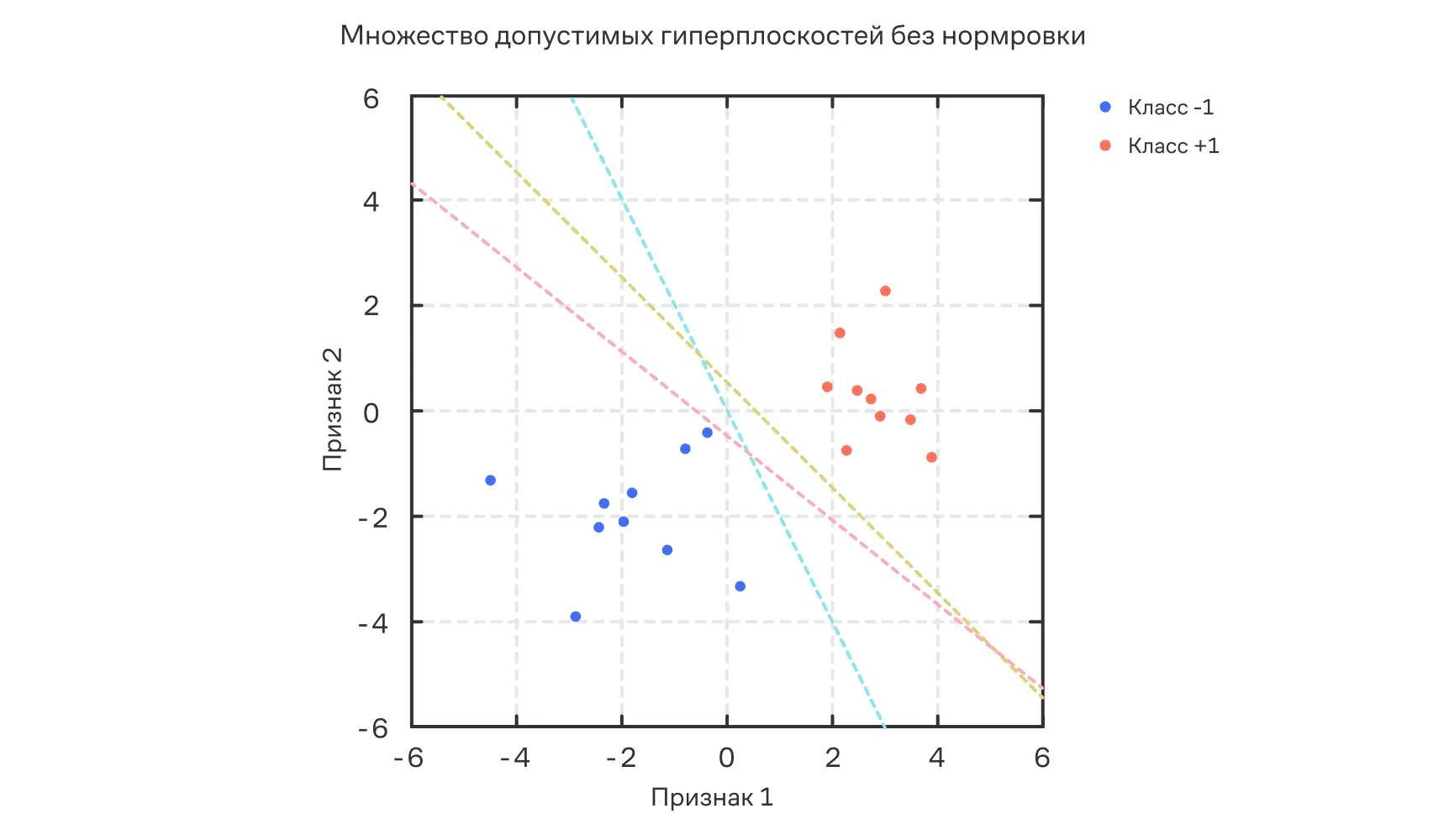
Примеры допустимых гиперплоскостей без нормировки
Чтобы устранить эту неоднозначность, вводится нормировка:
Теперь ближайшие к границе объекты (опорные векторы) лежат строго на гиперплоскостях , а минимальный зазор между ними будет выражен через .
Это ограничение:
- По-прежнему требует правильной классификации.
- Фиксирует масштаб — ближайшие к границе объекты (опорные векторы) должны лежать на уровне , а не где угодно.
- Гарантирует, что зазор можно выразить через .
Теперь выведем определение опорных векторов:
💡
Опорные векторы— это объекты, попадающие на границу или внутрь разделяющей полосы (зазора), а также объекты, попадающие не в свой класс. Они определяют положение разделяющей гиперплоскости в методе опорных векторов (SVM).
Именно опорные векторы удерживают гиперплоскость на месте — любые другие объекты не влияют на модель. Это одна из причин, почему SVM часто считается «разреженным» методом: решение зависит лишь от подмножества обучающих точек.
На графике ниже изображена разделяющая гиперплоскость (чёрная), границы зазора (пунктир), опорные векторы (обведённые). Они определяют решение задачи и лежат точно на границах зазора. Обратите внимание, что опорными векторами являются объекты, которые попали на границы зазора, внутрь него или попали не в свой класс.
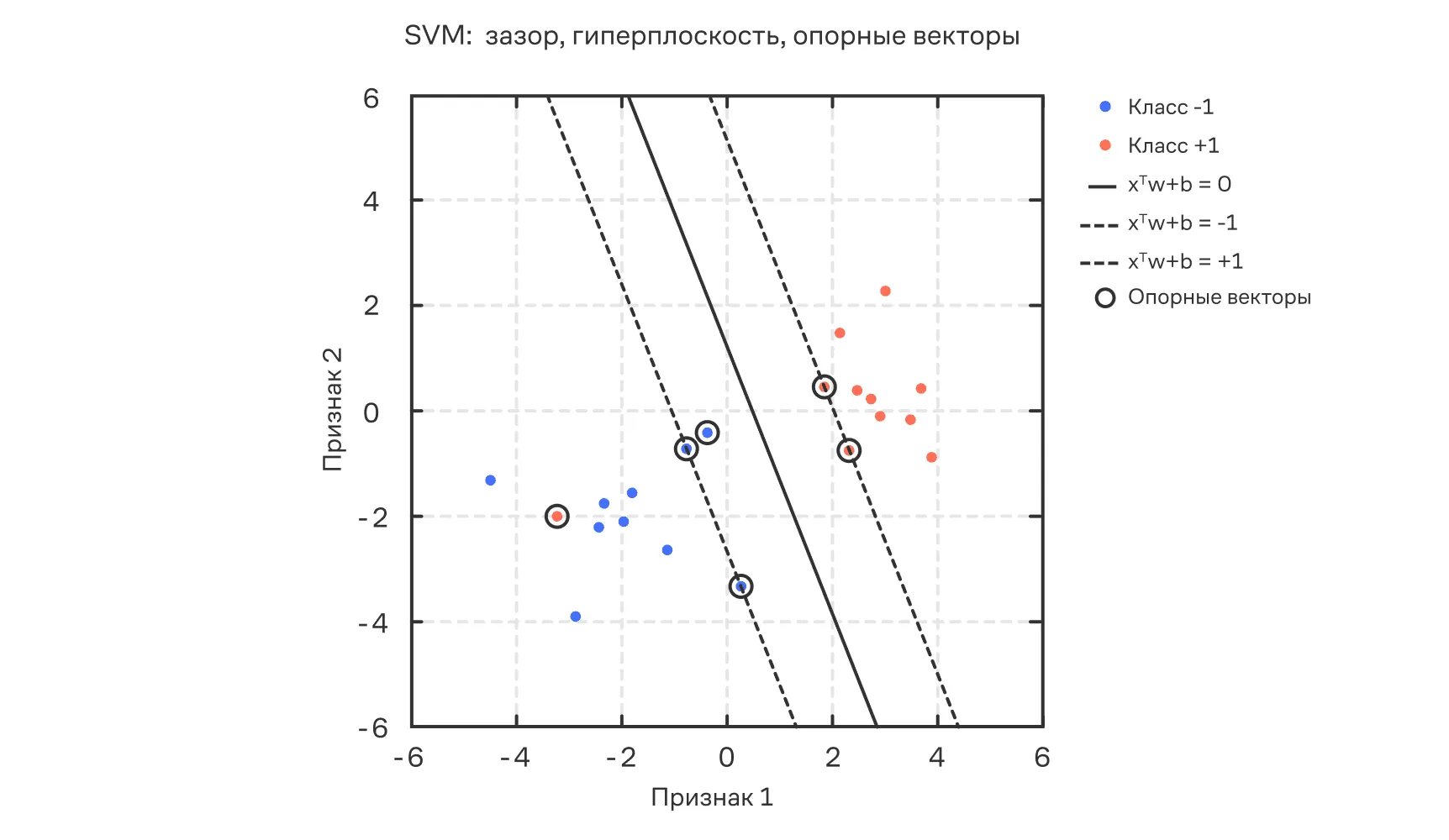
Пример решения задачи бинарной классификации с помощью SVM
Геометрический смысл: расстояние до гиперплоскости
Рассмотрим, почему задача SVM сводится к минимизации нормы вектора . Для этого нужно понять, что такое расстояние от точки до гиперплоскости. Пусть гиперплоскость задана уравнением:
Расстояние от произвольной точки до этой гиперплоскости выражается формулой:
Эта формула выводится следующим образом. Мы ищем проекцию точки на гиперплоскость вдоль нормали . Искомая проекция имеет вид:
Где — такое число, что , то есть:
Раскрывая скобки, получаем:
Теперь мы можем найти проекцию :
Значит, вектор от точки до гиперплоскости имеет длину:
Таким образом, расстояние от точки до гиперплоскости зависит только от значения , нормализованного по длине вектора .
После нормировки ближайшие точки лежат на гиперплоскостях:
Расстояние между этими двумя параллельными гиперплоскостями:
То есть геометрический зазор между классами в модели SVM равен , и задача обучения SVM становится задачей максимизации зазора, что эквивалентно минимизации .
Ниже — график, иллюстрирующий зазор и его размер. Он измеряется как расстояние между параллельными гиперплоскостями вдоль нормали и равен . Это расстояние определяет ширину разделяющей полосы в методе опорных векторов (SVM). Стрелка нормали указывает направление роста скалярного выражения .
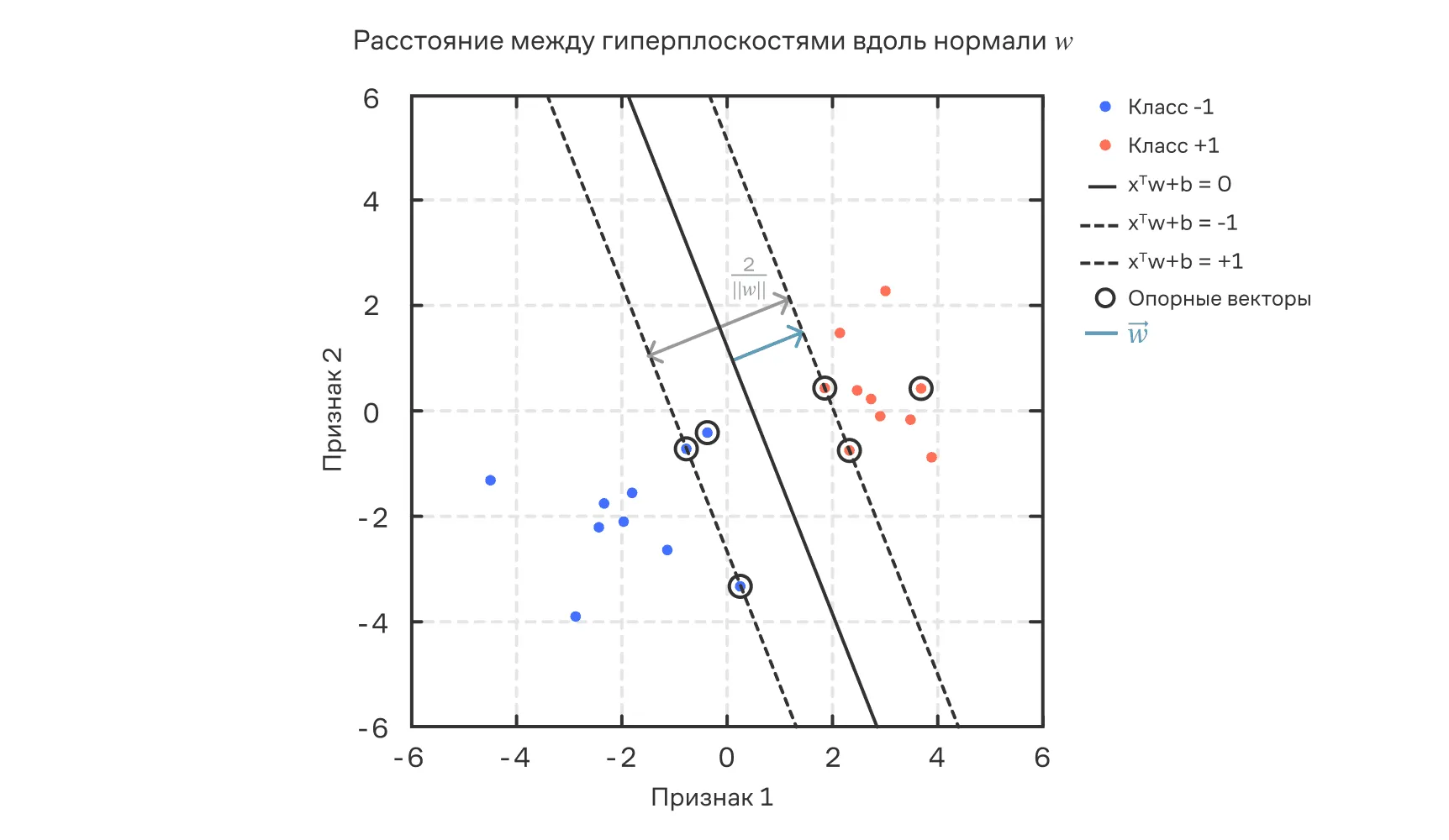
Геометрический зазор как расстояние между вдоль нормали
С учётом нормировки задача SVM записывается как:
Если данные не линейно разделимы, то в задачу вводятся переменные-допуски :
Гиперпараметр управляет штрафом за ошибки классификации: чем больше , тем менее терпима модель к нарушениям и тем более узким получается зазор. И наоборот, чем меньше , тем шире зазор и тем меньше SVM фокусируется на штрафах.
На графиках ниже наглядно показано влияние влияние гиперпараметра на ширину зазора в SVM. Ширина зазора при этом определяет набор опорных векторов. А они, в свою очередь, определяют положение и наклон разделяющей гиперплоскости.
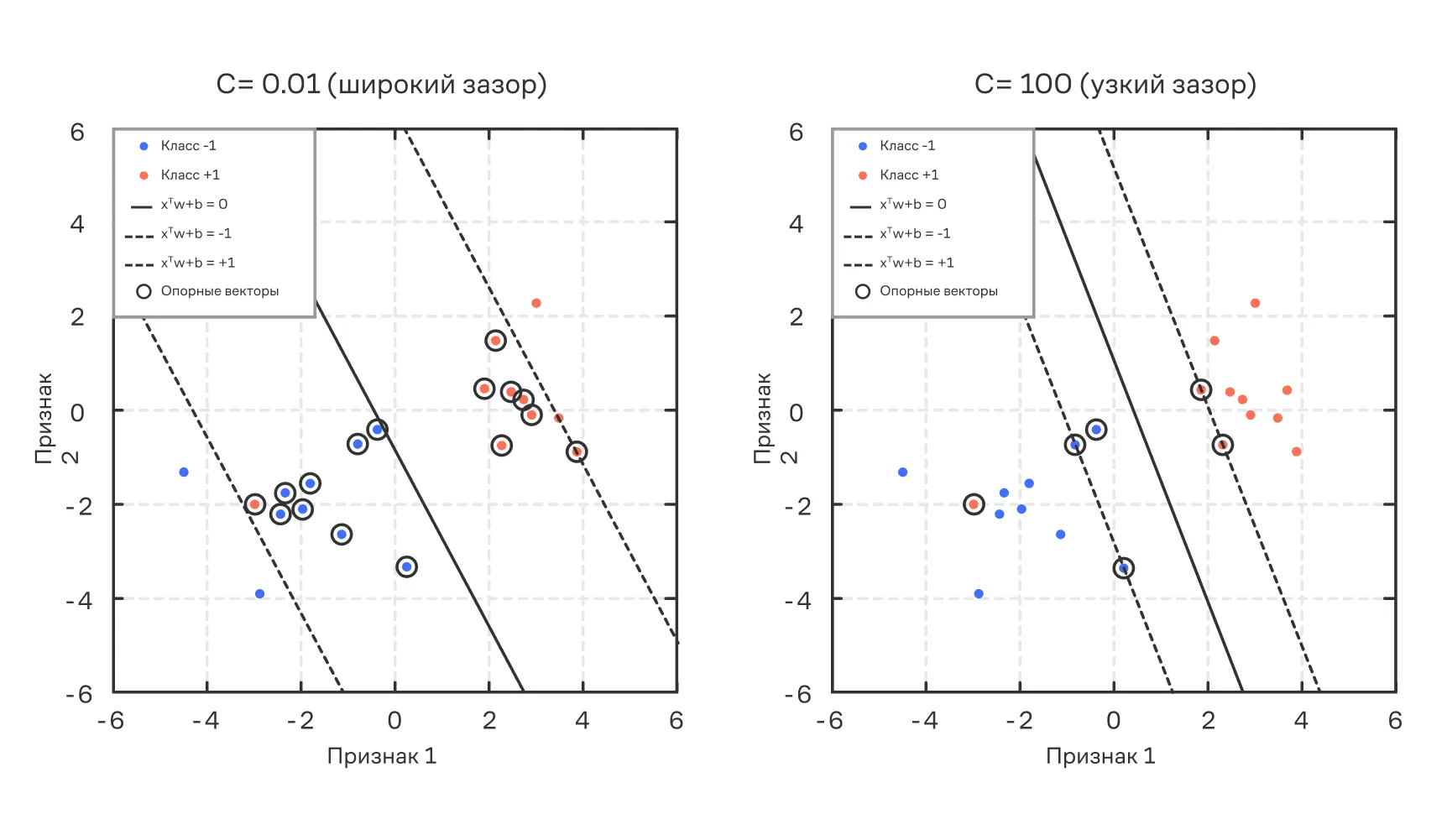
Влияние гиперпараметра на ширину зазора в SVM
Ниже мы подробно разберём, как метод опорных векторов (SVM) формулируется в так называемой двойственной форме — через лагранжиан, скалярные произведения и матрицу Грама. Это необходимо для понимания ядрового трюка, который позволяет обучать нелинейные модели, оставаясь в рамках линейной оптимизации.
Двойственная задача и матрица Грама
Прежде чем начнём, важное замечание.
💡Если вы только начинаете знакомство с SVM, не обязательно вникать во все математические детали: вы всё равно сможете пользоваться SVM и понимать его основные идеи.
Суть метода остаётся той же: мы ищем максимально разделяющую гиперплоскость между классами. Но если вы готовы немного углубиться в теорию оптимизации, этот раздел даст вам более глубокое понимание устройства метода.
Чтобы решать эту задачу эффективно, используют так называемый метод Лагранжа. Суть метода заключается в том, чтобы объединить целевую функцию и ограничения в одну вспомогательную функцию — лагранжиан — и затем искать её стационарные точки.
Вводятся множители Лагранжа для каждого ограничения. Лагранжиан записывается как:
Чтобы перейти к двойственной задаче, мы хотим выразить исходную оптимизацию только через переменные , исключив и . Для этого мы рассматриваем седловую точку лагранжиана: она должна быть минимумом по и при фиксированных и максимумом по при фиксированных :
Минимум по означает, что мы ищем точку, в которой градиент по этим переменным обращается в нуль. Рассмотрим выражение подробнее. Раскроем скобки:
Теперь вычислим градиент по :
Приравниваем производную к нулю (так как ищем минимум по ):
Аналогично по :
Именно эти два уравнения позволяют исключить и и перейти к двойственной задаче, которая зависит только от . Мы нашли выражения для и , при которых достигает минимума. Подставим их обратно в , чтобы получить оптимизационную задачу только по , — это и есть двойственная задача.
Далее рассмотрим линейную часть лагранжиана. Раскрыв скобки, подставим и учтём, что :
Теперь запишем итог, не забывая что линейная часть в лагранжиане была с минусом:
Здесь возникает ключевое наблюдение: вся задача выражена только через скалярные произведения . Это приводит нас к понятию матрицы Грама:
Если все объекты записаны в матрицу , то . Эта симметричная положительно полуопределённая матрица описывает геометрию выборки: углы, длины и взаимные расположения точек.
Предсказание новой точки тоже выражается только через скалярные произведения:
Большинство обнуляется, и только несколько объектов , у которых , влияют на решение — они и являются опорными векторами.
Рассмотрим следующий рисунок, который иллюстрирует ключевые компоненты двойственной задачи SVM — матрицу Грама и геометрию обучающих объектов в пространстве признаков. Советуем открыть его в отдельной вкладке, чтобы он был перед глазами: мы будем разбирать его до конца раздела.
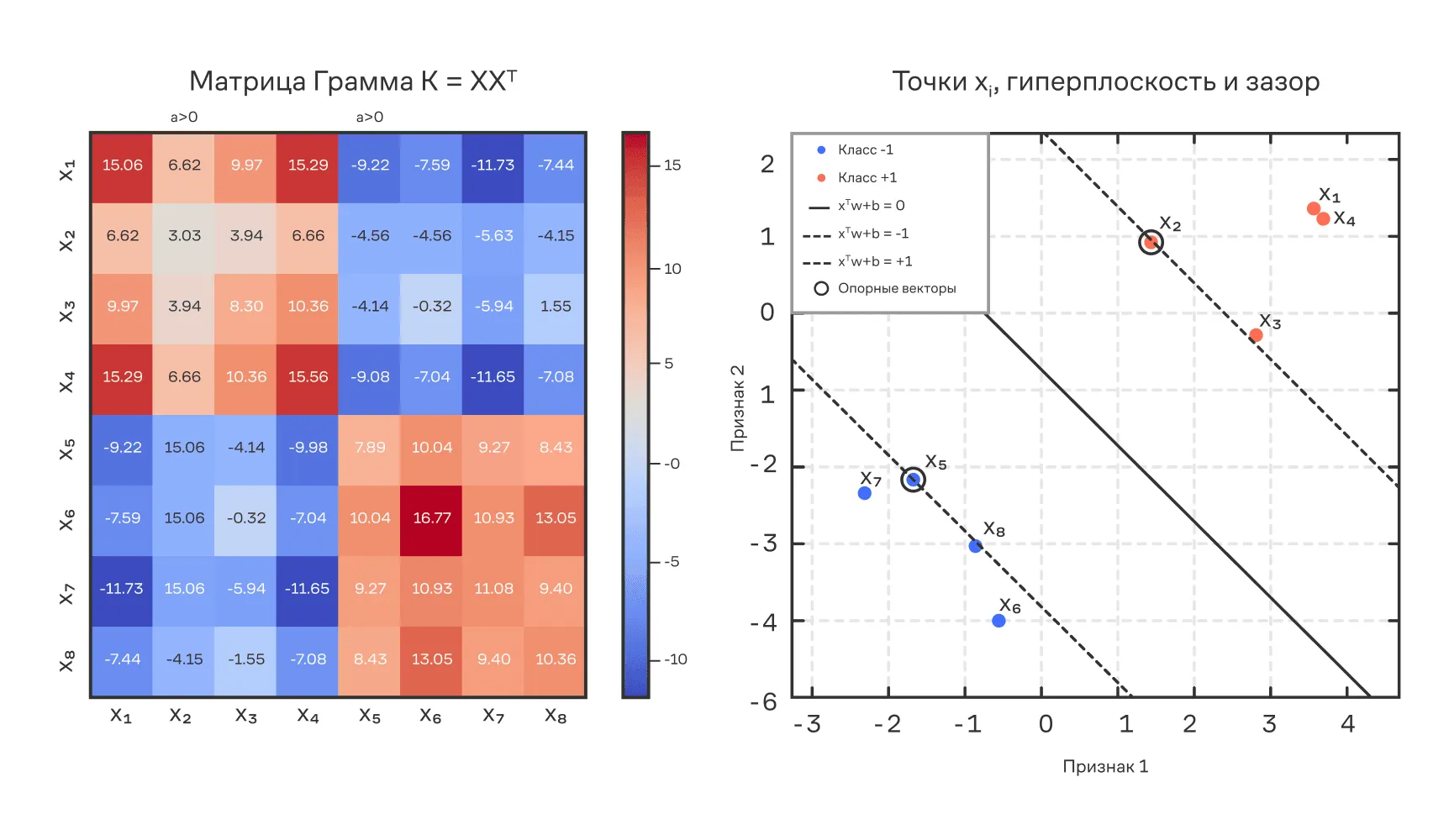
Двойственная задача SVM: матрица Грама (слева) и геометрия обучающих объектов с гиперплоскостью и зазором (справа). Опорные векторы () отмечены на обеих панелях
Слева представлена матрица Грама , а справа — расположение точек в пространстве , разделяющая гиперплоскость и границы зазора.
Каждая ячейка матрицы содержит скалярное произведение между парами объектов:
Таким образом, эта матрица отражает взаимную геометрию объектов: направление и относительную длину их векторов. Положительные значения (оттенки красного) соответствуют близким по направлению векторам, отрицательные (синие) — противоположно направленным. Симметричность отражает симметричность скалярного произведения.
Над отдельными столбцами подписано — это означает, что соответствующий объект является опорным вектором. Только такие объекты получают ненулевое значение в решении двойственной задачи и участвуют в предсказании новой точки :
Где означает, что учитываются только опорные векторы SV (Support Vectors).
Таким образом, левая часть рисунка показывает, что вся двойственная задача выражается через скалярные произведения и только несколько строк и столбцов (опорные векторы) действительно участвуют в модели.
Сопоставляя обе части рисунка, мы можем сделать вывод:
- Какие именно объекты оказываются опорными векторами (в обеих частях рисунка они выделены).
- Как они взаимодействуют с другими через матрицу скалярных произведений.
- Почему в двойственной формулировке SVM мы можем отказаться от явного и и оперировать только , , и .
Таким образом, рисунок подчёркивает центральную идею двойственной оптимизации: всё обучение сводится к манипуляции скалярными произведениями между входными объектами, и только несколько ключевых точек действительно влияют на результат.
Благодаря тому, что вся модель зависит только от , мы можем заменить это выражение на произвольное ядро и тем самым перейти к нелинейным признаковым пространствам, не покидая двойственной формы. Матрица Грама тогда становится ядровой матрицей, а алгоритм — ядровым SVM.
Ядровой трюк: нелинейные разделяющие границы
Если данные неразделимы линейно, их можно отобразить в другое пространство — возможно, гораздо большей размерности — с помощью отображения . Тогда все скалярные произведения заменяются на .
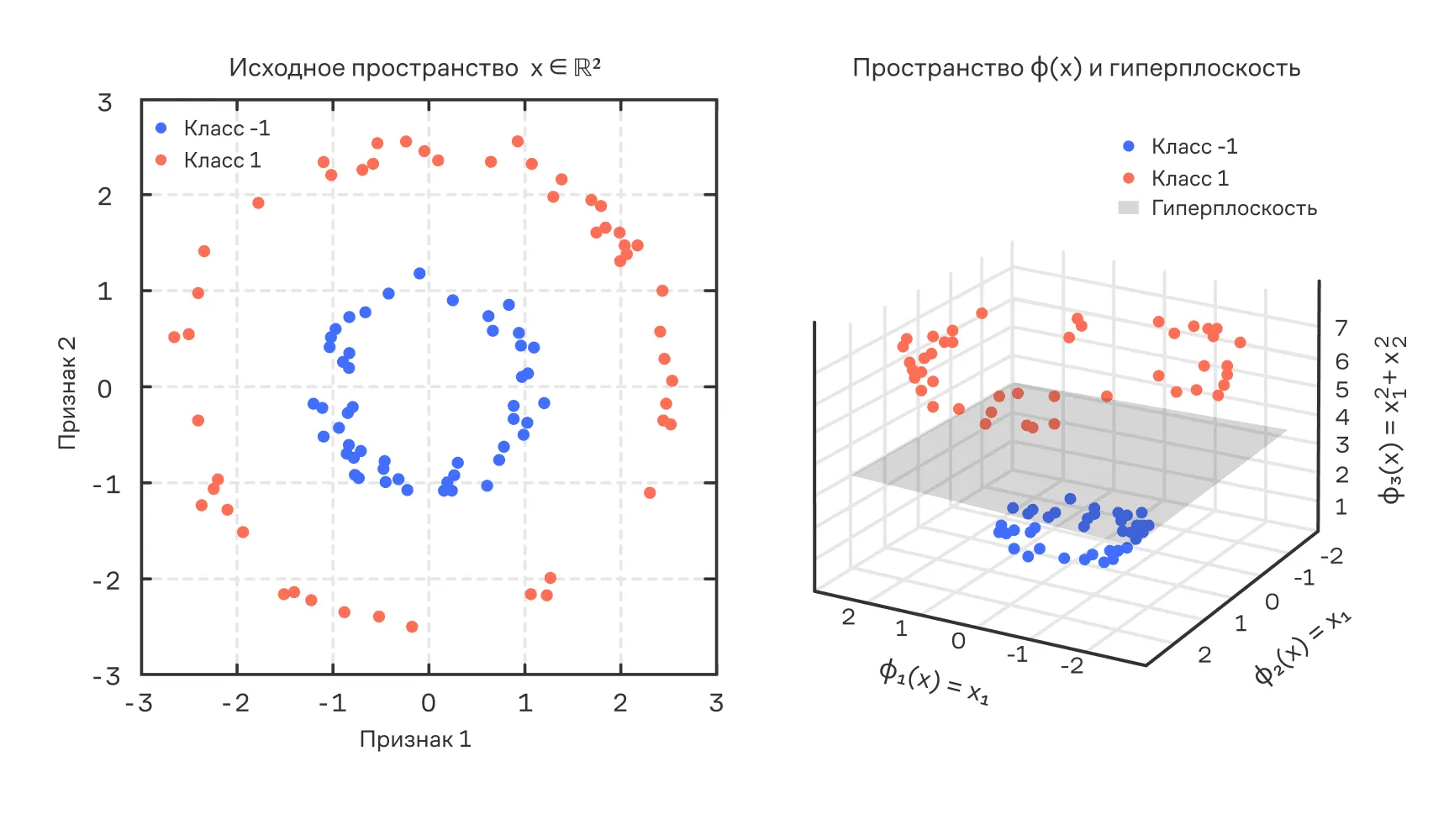
Иллюстрация ядрового трюка: в исходном пространстве классы не разделимы линейно (слева), но после отображения становится возможна линейная разделяющая гиперплоскость (справа)
Но если существует функция , то можно вычислять это произведение напрямую, без знания . Это и есть ядровой трюк.
Где — отображение признаков в более богатое пространство. При этом явно вычислять не нужно: достаточно знать значения .
Типичные ядра:
- Полиномиальное .
- Гауссовское (RBF): .
- Сигмоидальное: .
Модель остаётся линейной в новом пространстве, но может реализовывать нелинейную границу ****в исходном. Все вычисления идут через матрицу Грама , составленную из ядер.
На рисунке ниже представлен пример применения SVM для линейно неразделимых данных с использованием SVM с полиномиальным ядром второй степени. Опорные векторы показаны окружностями, пунктир обозначает границы зазора , жирная линия — границу классов .

Нелинейная граница, построенная SVM с полиномиальным ядром степени 2
Обобщающая способность и VC-размерность
Наконец, важный вопрос: если можно использовать произвольно сложное отображение, не приведёт ли это к переобучению? Теория обобщения отвечает на это с помощью понятия размерности Вапника — Червоненкиса (VC-размерности).
💡
VC-размерность— это мера сложности класса бинарных классификаторов, основанная на том, сколько различных размеченных выборок класс может идеально классифицировать.
Линейный классификатор в имеет VC-размерность Например, любые три точки, не лежащие на одной прямой, в двумерном пространстве могут быть разделены на два класса всеми возможными способами (их всего ). Но не всякие четыре точки в двумерном пространстве могут быть разделены линейным классификатором. Поэтому VC-размерность линейного классификатора в двумерном пространстве равна .
Внизу показана визуализация VC-размерности: три точки можно разделить линейной гиперплоскостью при любой разметке классов (слева), а для четырёх точек (справа) не существует гиперплоскости, корректно разделяющей все возможные разметки.
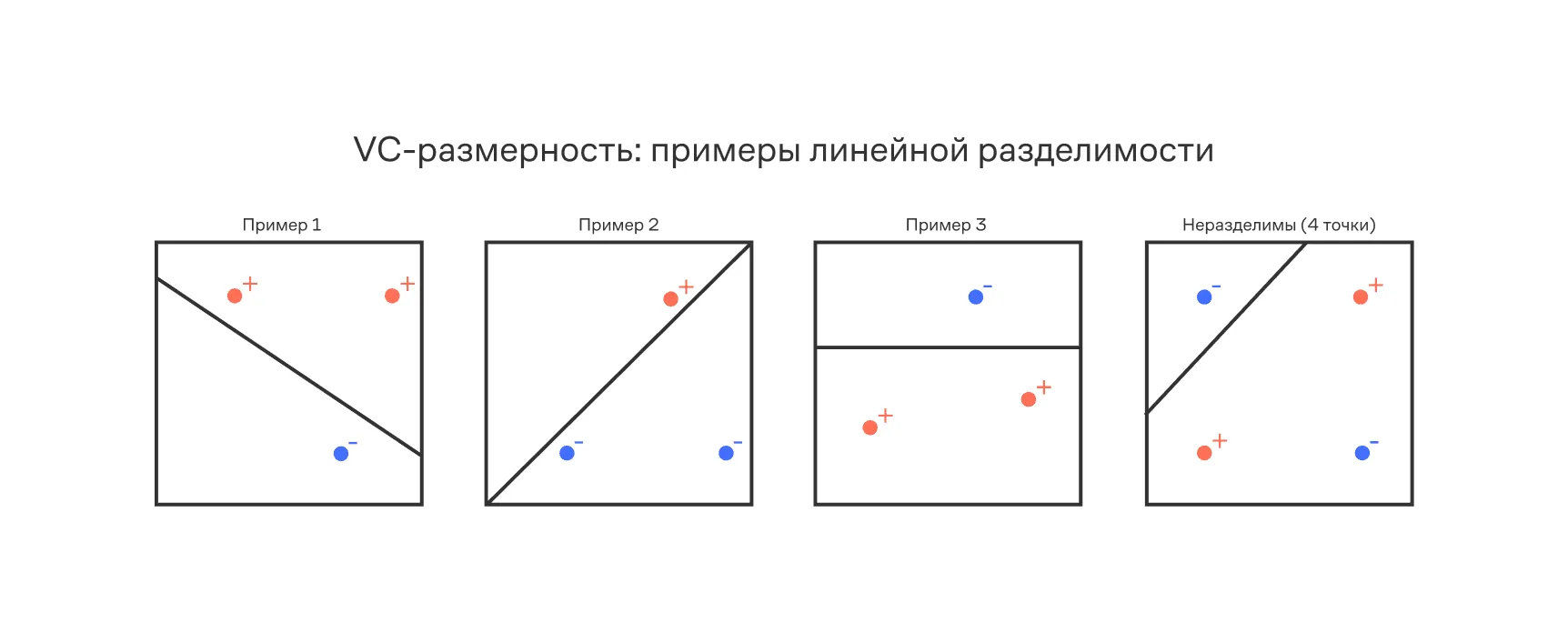
Иллюстрация VC-размерности
VC-размерность отражает способность модели подстраиваться под шум. Чем выше VC-размерность, тем более гибкой (и потенциально более склонной к переобучению) является модель.
Переобучение возникает, когда модель слишком хорошо запоминает обучающую выборку, включая шум или нерелевантные детали, и плохо обобщает на новых данных. Например, полиномиальный классификатор высокой степени имеет огромную VC-размерность и может идеально подогнаться под выборку, но при этом не улавливать общие закономерности.
При использовании ядровых методов мы фактически работаем в пространстве гораздо большей (а иногда и бесконечной) размерности. Это может увеличить VC-размерность. Но SVM остаётся устойчивым к переобучению за счёт максимизации зазора: среди всех границ модель выбирает ту, что наиболее проста геометрически.
То есть максимизация зазора — это форма регуляризации, аналогичная ограничению нормы весов в линейной регрессии. Она снижает эффективную сложность модели, даже если номинальная VC-размерность высокая из-за ядра. SVM в целом не зависит от всей выборки, а только от ее малой части — опорных векторов, и потому он не склонен подгоняться к каждой точке обучающей выборки.
Реализация в Python
Вот как реализовать метод SVM с помощью библиотеки scikit-learn:
1from sklearn.svm import SVC
2import numpy as np
3
4# Пример обучающих данных
5np.random.seed(0)
6X_pos = np.random.randn(10, 2) + [2, 0]
7X_neg = np.random.randn(10, 2) + [-2, -2]
8
9X = np.vstack([X_pos, X_neg])
10y = np.array([1]*10 + [-1]*10)
11
12# Обучение линейного SVM
13model = SVC(kernel='linear', C=1.0)
14model.fit(X, y)
15
16w = model.coef_[0] # Вектор весов
17b = model.intercept_[0] # Смещение
18sv = model.support_vectors_ # Опорные векторы
19
20print(f"w = {w}, b = {b}")
21
22# Предсказание для новой точки
23x_new = np.array([[4, 4]])
24prediction = model.predict(x_new)
25print(f"Предсказанный класс для {x_new} = {prediction[0]}")
Мы увидели, что SVM строит разделяющую гиперплоскость с максимальным зазором, — это эквивалентно минимизации нормы весов. В двойственной форме всё сводится к скалярным произведениям и матрице Грама, а ядровой трюк позволяет получать нелинейные границы, оставаясь в линейной оптимизации. На решение влияют лишь опорные векторы, а сложность модели контролируется параметром и выбором ядра, его параметров.
На практике качество SVM критически зависит от свойств признаков: масштабов, центра и выбросов. Поскольку и скалярные произведения, и ядровые расстояния (например, в RBF-ядре) чувствительны к масштабам, несбалансированные признаки ведут к ухудшению зазора, нестабильному набору опорных векторов и сложной настройке гиперпараметров.
Поэтому следующий шаг — препроцессинг признаков: центрирование и стандартизация, Min-Max и робастное масштабирование, а также их влияние на обусловленность , устойчивость решения и скорость сходимости.
В следующем параграфе мы разберём эти приёмы и покажем, как правильно встраивать их в конвейер обучения, чтобы избежать утечек и получить предсказуемый выигрыш в качестве.


