В этом параграфе мы научимся смотреть на граф не просто как на набор вершин и рёбер, а как на пространство, по которому могут распространяться сигналы подобно тому, как звук распространяется в физической среде. Этот подход, известный как обработка сигналов на графах (Graph Signal Processing), позволяет применять идеи из физики для анализа сложных сетей.
Мы разберём:
- Спектр графа. Введём понятие графового лапласиана и разберёмся, почему его собственные значения можно трактовать как некие «частоты» графа, а собственные векторы — как его основные «моды» колебаний.
- Графовое Фурье-преобразование. По аналогии с классическим анализом сигналов мы научимся раскладывать данные на графе по базису из собственных векторов.
- Диффузионные процессы и случайные блуждания. Мы изучим, как информация растекается по графу со временем и как это связано с такими алгоритмами, как PageRank.
- Графовые фильтры. Мы рассмотрим, как можно обрабатывать сигналы на графах, усиливая или ослабляя определённые частотные компоненты для выделения нужных структур.
Прочитав этот параграф, вы сможете анализировать глобальную структуру графа с помощью его спектра. Например, для оценки связности сети или поиска сообществ. Вы поймёте, как моделируются динамические процессы на сетях: от распространения мнений в соцсетях до ранжирования веб-страниц. Всё это даст вам прочную математическую базу для понимания работы графовых свёрточных сетей (GCN) и других современных методов графового машинного обучения.
Теперь, когда цели ясны, самое время начать!
Спектр графа и диффузионные процессы
Как устроен граф? Насколько он связен? Есть ли в нём сообщества, или, напротив, он весь почти распадается? Представьте, что граф — это музыкальный инструмент, например гитара.
Когда вы играете на инструменте, дёргая струны, он звучит на своем уникальном наборе резонансных частот. Вот и граф, если его представить как колеблющуюся систему, имеет свои частоты вибрации. Эти частоты и есть собственные значения. А вместе они дают спектр графа — как спектр излучения или звука.
И эта аналогия с частотами не просто красивая метафора: на ней построено целое научное направление, которое позволяет анализировать данные на графах так же строго, как инженеры анализируют звуковые или радиосигналы.
В теории графов это направление называется обработкой сигналов на графах (англ. Graph Signal Processing, GSP). Оно расширяет традиционную обработку сигналов на случай, когда данные представлены в виде графов.
Прежде чем погружаться в математику, давайте посмотрим на GSP в действии.
Представьте умный дом с десятками датчиков температуры. Один датчик установлен неудачно и стабильно «шумит» на пару градусов. Если принять его значение за истину, система климат-контроля начнёт ошибаться.
Идея GSP проста: мы доверяем не одному числу, а сети в целом. Значение в узле корректируется с оглядкой на соседей по графу (план дома), поэтому наш выбивающийся датчик мягко подтягивается к согласованной картине. В итоге мы получаем устойчивые оценки и корректное управление.
Кроме того, GSP применяется и в других областях:
- Нейробиология (ЭЭГ/МРТ). Мозг моделируют здесь как граф функциональных/структурных связей. GSP помогает фильтровать шумы в сигналах, выделять сообщества нейронов, образующие паттерны активности, и локализовать источники сигналов.
- Социальные сети. Анализ и моделирование диффузии новостей или мнений, выявление источников и влиятельных пользователей, фильтрация бот-активности, улучшение рекомендаций.
- Транспортные системы. Трафик рассматривается как сигнал на узлах/рёбрах дорожного графа. GSP используют для краткосрочного прогноза пробок, обнаружения аномалий и оптимизации маршрутов или светофорных планов.
Все эти задачи объединяет одна простая идея: чтобы понять сигнал, нужно учитывать структуру сети, по которой он распространяется. Давайте теперь разберём ключевые математические инструменты и принципы, которые позволяют это делать.
В общем случае сигналом на графе будем называть вектор значений на вершинах . Чтобы фильтровать, сглаживать или извлекать структуру из таких сигналов, нужно ввести понятие частот на графе — аналогов синусоид в классическом Фурье-анализе.
Но откуда берутся сами синусоиды в классическом анализе? Они являются собственными функциями оператора Лапласа $\Delta$ — то есть функциями, которые этот оператор лишь растягивает, не меняя их формы. Эта идея даёт нам ключ к решению: чтобы найти частоты на графе, нам нужно сначала определить графовый аналог оператора Лапласа, а затем найти его собственные векторы.
Для привычных нам функций оператор Лапласа интуитивно можно воспринимать как меру отклонения значения функции в точке от её среднего значения в малой окрестности этой точки.
💡Для функции двух переменных , оператор Лапласа (или лапласиан) определяется как сумма её вторых частных производных:
В общем случае для функции переменных он является дивергенцией её градиента и равен сумме всех чистых вторых производных:
Знак лапласиана показывает, как значение функции в точке соотносится со средним по её соседям:
- Если лапласиан в точке большой и положительный, то функция в этой окрестности вогнута, похожа на яму, и её значение в центре меньше среднего по окрестности.
- Если отрицательный — функция выпукла, словно похожа на холм, и значение в центре больше среднего.
Граница между этими случаями — нулевое отклонение. Уравнение Лапласа определяет гармонические функции: в каждой точке их значение совпадает со средним по малой окрестности. В физике это соответствует стационарному режиму — например, из уравнения теплопроводности при остаётся ; аналогично для электростатического потенциала в областях без зарядов.
От этой непрерывной картины перейдем к дискретной. Для неориентированного взвешенного графа с матрицей смежности , где , графовый лапласиан, или матрица Кирхгофа, задаётся как:
здесь — диагональная матрица взвешенных степеней вершин, где .
Действие графового лапласиана на сигнал (вектор значений на вершинах) раскрывает суть самой матрицы:
Эта формула наглядно показывает, что лапласиан измеряет несогласованность значения в вершине со значениями её соседей, взвешенную по силе связей. Это и есть прямой дискретный аналог оператора Лапласа.
Часто в алгоритмах используют и нормализованные варианты лапласиана, которые понадобятся нам в дальнейшем:
Кстати, второе название — «матрица Кирхгофа» — не случайно. Если представить взвешенный граф как электрическую сеть, где вершины — это узлы, а вес ребра — это проводимость (величина, обратная сопротивлению) между ними, то система уравнений, описывающая токи в сети на основе законов Кирхгофа, примет в точности ту же матричную форму, что и лапласиан.
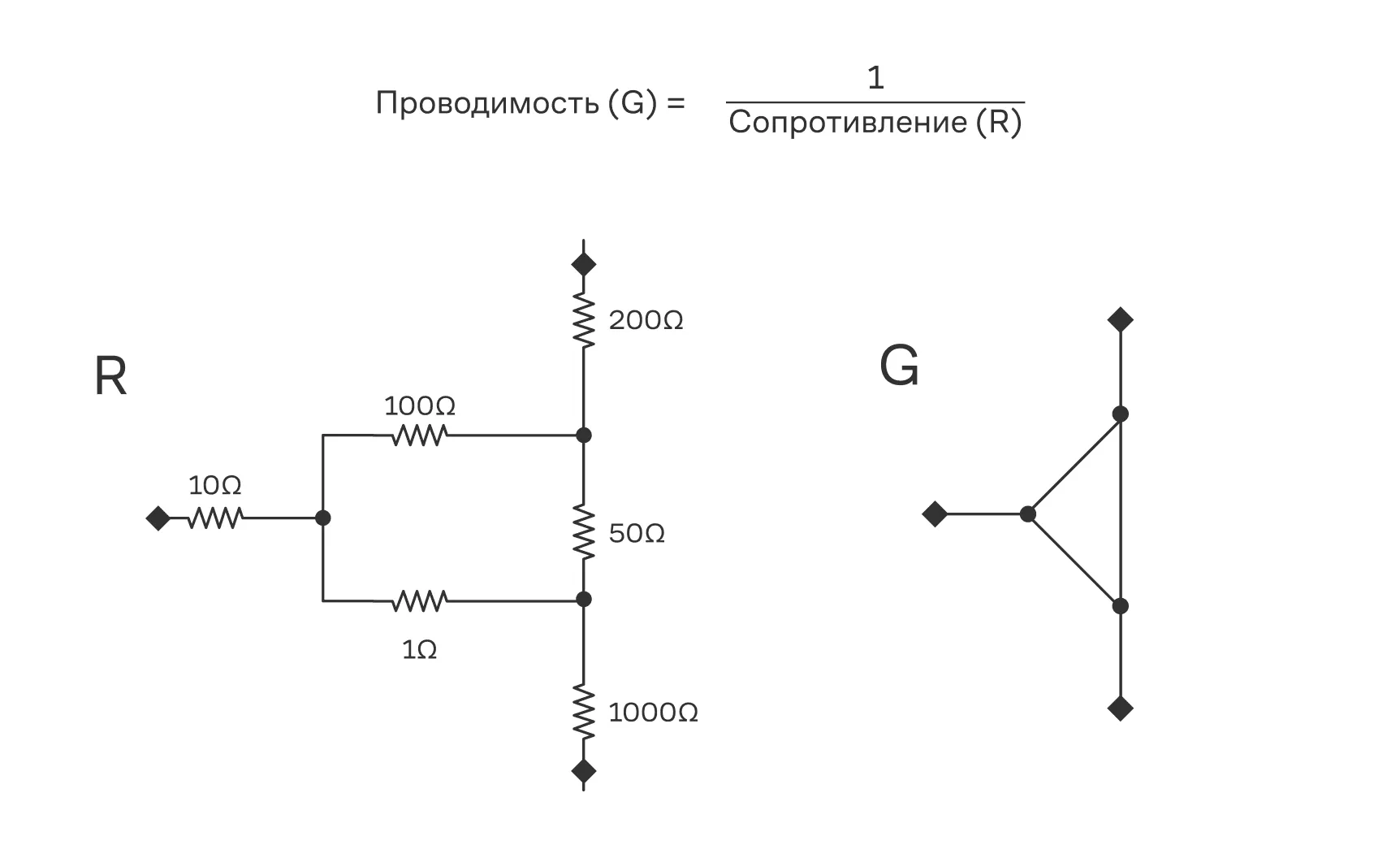
Слева — схема электрической цепи (резистивной сети), справа — её эквивалентное представление в виде графа.
Эта глубокая связь позволяет применять аппарат линейной алгебры к физическим задачам и наоборот.
Связь с физикой и комбинаторикой
Электрические сети. Если веса рёбер — это проводимости, то — узловая матрица проводимостей. Эффективное сопротивление между вершинами и выражается через псевдообратную матрицу : .
Теорема о деревьях. В комбинаторике, по теореме Кирхгофа, любой алгебраический кофактор матрицы — минор с правильным знаком — равен числу остовных деревьев в графе.
Дальше воспользуемся этим и изучим собственные векторы и значения получившейся матрицы:
Здесь назовем модами графа, а — частотами. Именно этот набор собственных значений и составляет то, что формально называют спектром графа.
💡Спектром графа называется мультимножество, или упорядоченный набор, собственных значений его графового лапласиана. Этот набор чисел является своего рода визитной карточкой, которая несёт в себе информацию о ключевых структурных свойствах графа.
Теперь, когда у нас есть формальное определение, давайте разберём ключевые свойства спектра. Для этого упорядочим собственные значения лапласиана по возрастанию:
Вот что они нам говорят о структуре графа:
- Число нулевых собственных значений равно числу компонент связности графа. Если граф связен, то — единственный нулевой элемент спектра.
- Второе собственное значение () — это алгебраическая связность, или число Фидлера. Оно показывает, насколько хорошо граф связан в целом: тогда и только тогда, когда граф связен. Чем больше , тем труднее разрезать граф на две части. Соответствующий собственный вектор (вектор Фидлера) используется для спектральной кластеризации.
Давайте посмотрим, как эти теоретические свойства работают на практике. Рассмотрим на примере Karate Club — классического графа из социологического исследования Уэйна Захари (1977), описывающего взаимодействия членов университетского клуба карате. Вершины представляют участников клуба, рёбра — дружеские связи.
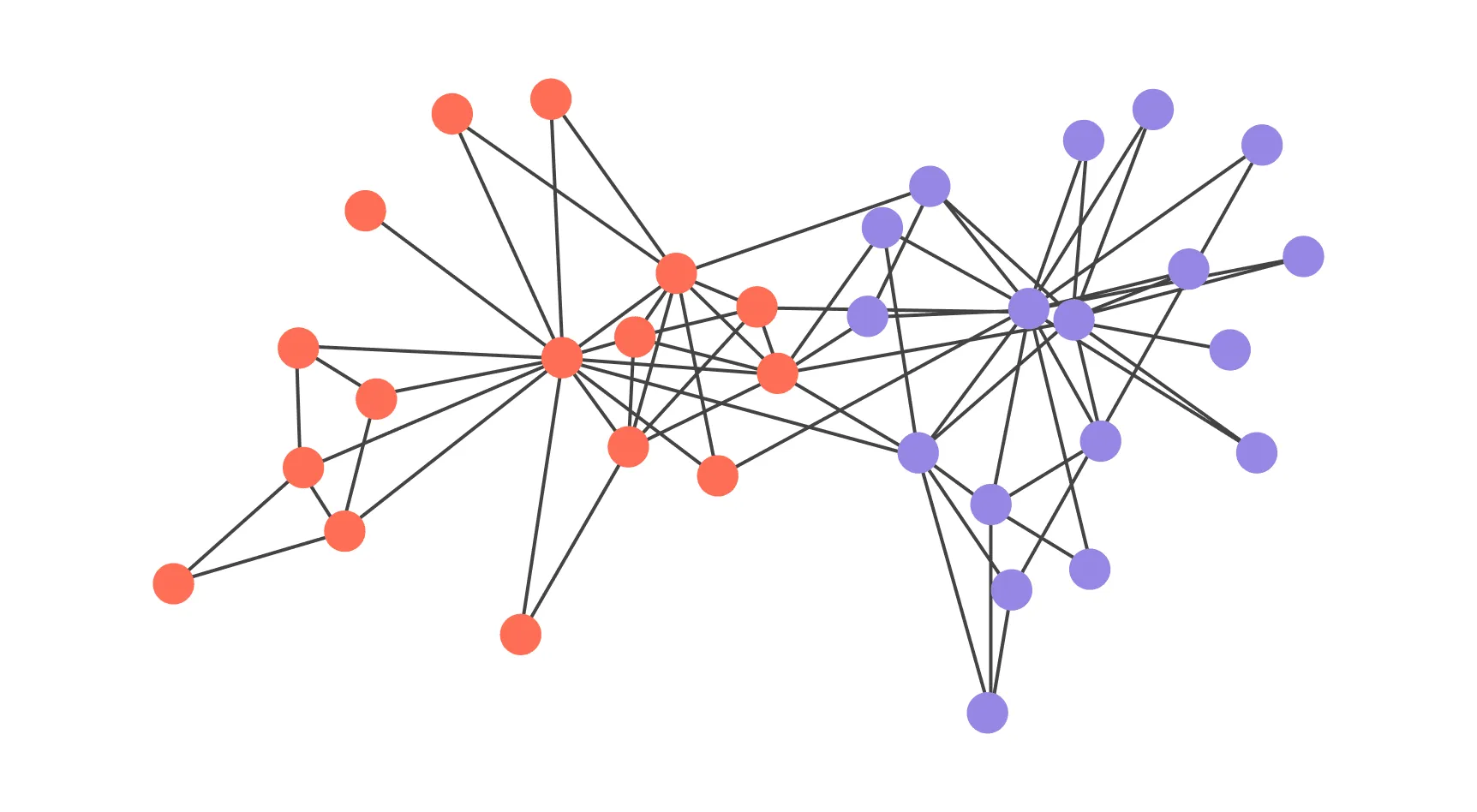
Визуализация спектрального разбиения графа «Клуба карате». Цвета соответствуют двум сообществам, определённым по знаку компонент вектора Фидлера.
В примере:
- Граф связен, поэтому в спектре лапласиана ровно один нуль ( кратности 1).
- Второе собственное значение указывает на общую связность и «хрупкость» разреза: чем оно больше, тем труднее разделить клуб на две большие части.
- Вектор Фидлера даёт одномерную координату для каждой вершины: разделение по знаку (или порогу) компонент разбивает граф на две группы, что хорошо согласуется с реальным расколом клуба, который произошёл в результате конфликта между инструктором и администрацией.
Практически это выглядит так: строим (или ), считаем собственные пары, сортируем , берём и делим вершины по знаку его компонент — получаем разбиение, которое визуально совпадает с историческим разделением в клубе.
Мы только что увидели, как всего один собственный вектор () помог нам понять глобальную структуру графа. Это подводит к логичному вопросу: а что, если использовать не один, а все собственные векторы сразу?
Оказывается, они обладают фундаментальным свойством: собственные векторы лапласиана образуют ортонормированный базис, по которому можно разложить любой сигнал на графе.
Графовое Фурье-преобразование (GFT)
Пусть — спектральное разложение графового лапласиана. Тогда графовое Фурье-преобразование задаётся парой операций:
Здесь — спектральные коэффициенты на частотах . Малые соответствуют гладким (низкочастотным) компонентам (значения в соседних вершинах близки), большие — осциллирующим (высокочастотным).
Гладкость сигнала удобно измерять квадратичной формой лапласиана:
Из формулы видно, что, подавляя компоненты с большими , мы выполняем низкочастотную (low-pass) фильтрацию и тем самым сглаживаем сигнал.
Замечания:
- Для связного графа . DC-компонента: для невзвешенного ; для симметрически нормализованного — .
- Далее, говоря о GFT и фильтрах, будем использовать базис собственных векторов — это удобно для ортонормировки.
- Полная спектральная декомпозиция дорога (), поэтому на практике применяют полиномиальные приближения (например, Чебышёв), к которым мы вернёмся в разделе про фильтры.
Этот аппарат и есть отправная точка для свёрток, фильтров и графовых нейросетей (GNN).
💡
GNN(англ. Graph Neural Networks, графовые нейронные сети) — это архитектура глубокого обучения, которая обрабатывает данные на графах, учитывая как признаки вершин и рёбер, так и их структуру.Подробно о GNN можно прочитать в соответствующей главе хендбука по машинному обучению.
Кроме того, спектральное представление напрямую связывает структуру графа с динамическими процессами на нём. Один из важнейших примеров таких процессов — это диффузия: постепенное сглаживание сигнала за счёт обмена значениями между соседними вершинами.
Диффузия
В классической диффузии (например, теплопроводности) скорость изменения температуры в точке пропорциональна разности между её значением и значениями соседей. На примере с сетью IoT-датчиков можно думать про это так, что в одной комнате включили обогреватель и теперь тепло растекается по нашему графу.
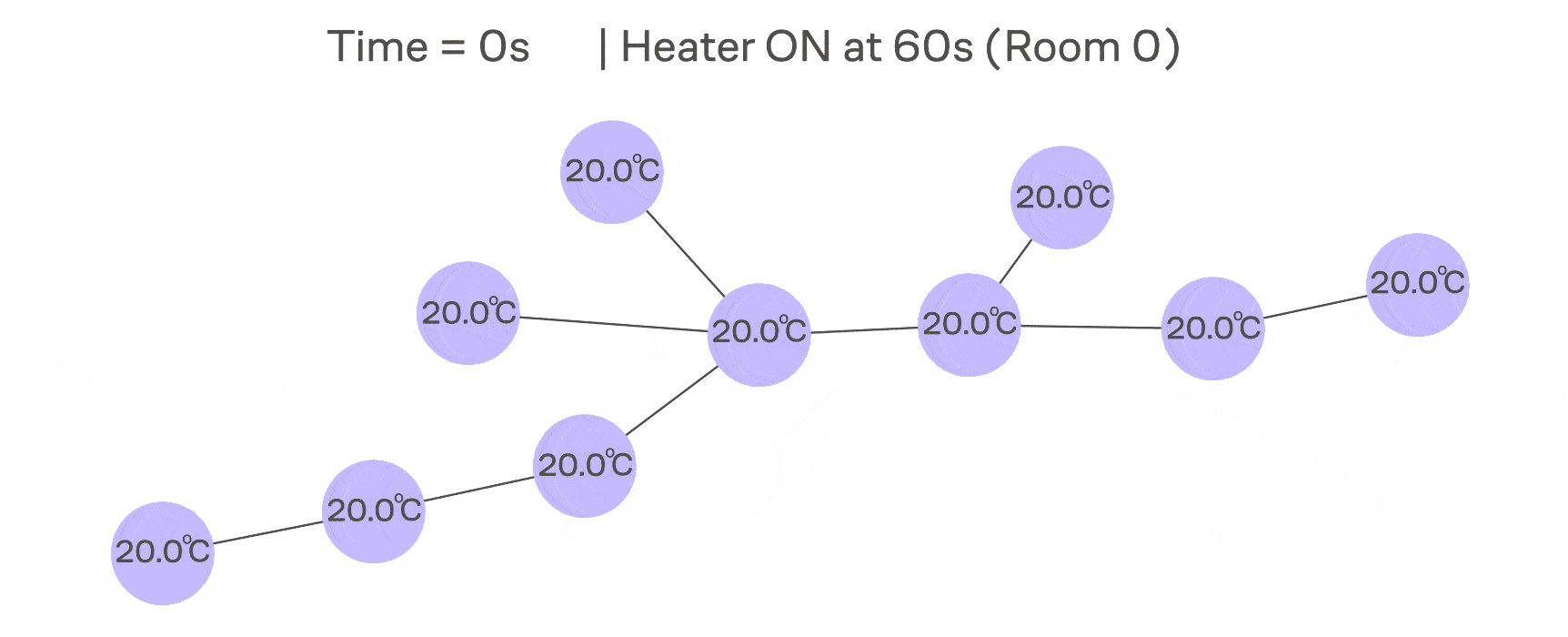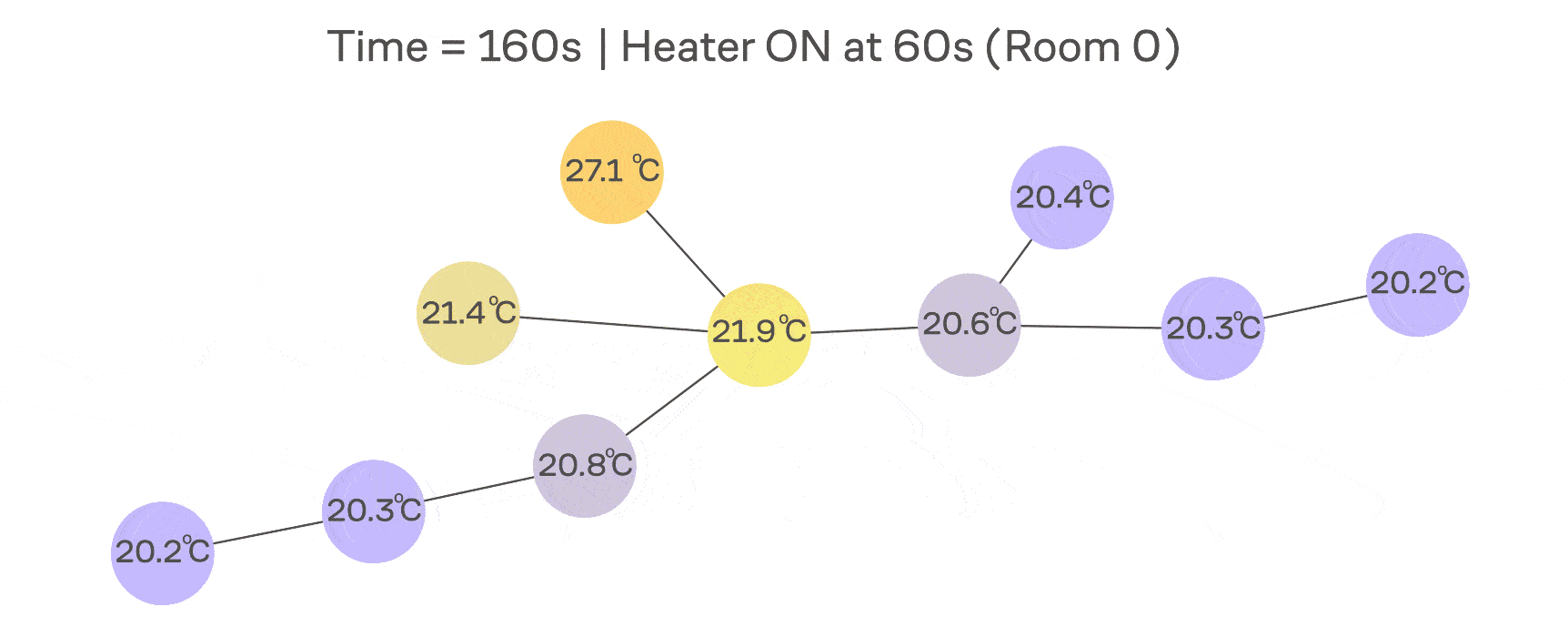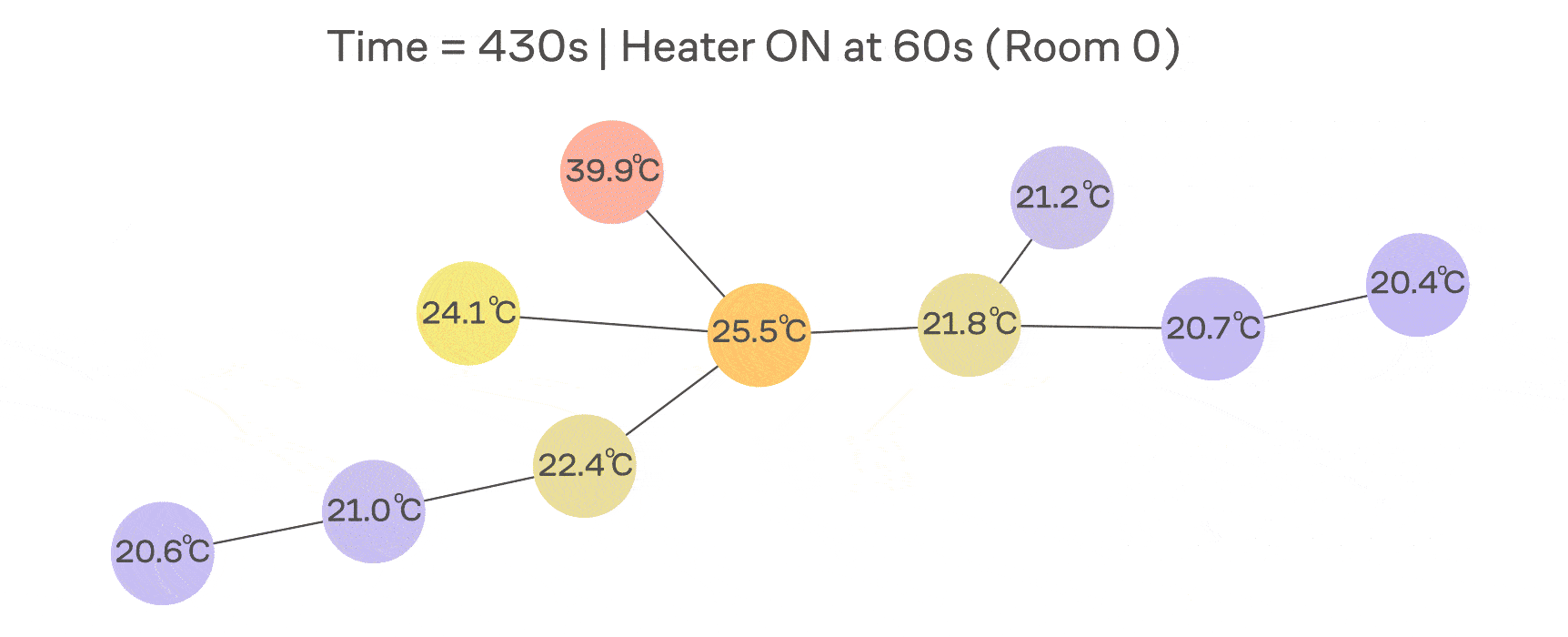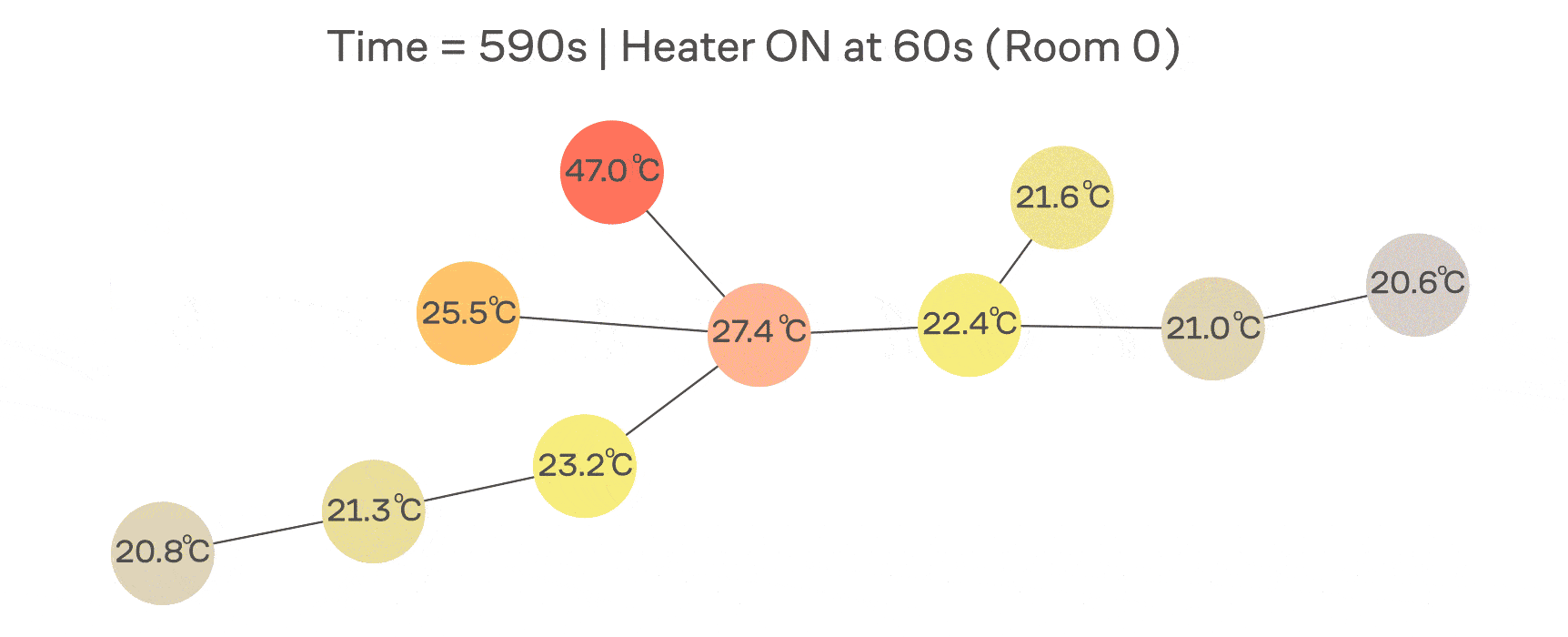
Формализуем эту идею через дифференциальное уравнение:
где:
- — значение вектор-столбца сигнала (температуры) в вершине ;
- — соседи вершины ;
- — вес ребра.
В матричной форме это уравнение элегантно записывается через графовый лапласиан:
Решением этого уравнения будет:
а матрицу называют оператором теплопроводности (англ. heat kernel). Эта матрица является некоторой машиной времени: она берёт начальный сигнал и показывает, как он будет выглядеть после растекания по графу в течение времени .
Полезно взглянуть на решение в спектральной базе. Пусть . Тогда
Эта формула наглядно показывает, что низкочастотные компоненты (где малы) затухают медленно, а высокочастотные (где велики) — очень быстро. Это и есть суть low-pass-сглаживания, которое неразрывно связывает диффузию со спектром графа.
Посмотрим на диффузию с другой стороны — как на усреднение по соседям. Тогда мы хотим, чтобы сигнал в вершине на следующем шаге был средним значением сигналов её соседей, нормированным на их количество. Это приводит к матрице
где каждая строка нормируется так, что . Эта матрица называется матрицей перехода, и она описывает случайное блуждание по графу: — вероятность перейти из вершины в вершину .
Как случайное блуждание может быть полезным
На самом деле случайное блуждание в машинном обучении встречается сплошь и рядом. Во временных рядах ситуацию, когда значение временного ряда предсказывают как значение на прошлом шагу плюс некий случайный шум, тоже иногда называют случайным блужданием.
В графах мы будем использовать случайные блуждания дальше для получения признакового описания графа. В путешествиях вы часто гуляете по городу, чтобы потом описать его друзьям. А чем графы хуже и почему бы по ним тоже не «погулять»?
А как матрица перехода связана с диффузией? Если мы хотим моделировать диффузию дискретными шагами времени, то новое состояние можно получить как:
Это дискретный аналог уравнения . Давайте теперь перепишем в ином виде:
где — единичная матрица. Теперь можно ввести понятие нормализованного несимметричного, или лапласиана случайного блуждания (англ. random walk):
Наш процесс теперь можно переписать в виде:
А при малых шагах и вовсе получим уже известное уравнение:
Остановимся поподробнее на случайном блуждании. В случае достаточно удачного графа, а именно:
- Из каждой вершины можно добраться до любой другой.
- Для дискретных графов блуждание положительно возвратное (вероятность вернуться в это же состояние когда-нибудь в будущем больше нуля) и апериодическое.
- Вероятности переходов между узлами положительные.
Что произойдёт, если мы будем совершать очень много шагов по графу? Если граф связен и не имеет «патологических» периодических структур (является апериодическим), то после множества шагов вероятность оказаться в любой вершине перестанет меняться и сойдётся к стационарному распределению .
Стационарное распределение — это такое распределение вероятности, которое не меняется с течением времени. Такое «вектор-строка»-распределение удовлетворяет уравнению
Иными словами, стационарное распределение — нормированный на 1 собственный вектор матрицы при собственном значении 1.
В случае ненаправленного связного графа с положительными весами получаем
где — степень вершины . Это означает, что в долгосрочной перспективе вероятность оказаться в конкретной вершине пропорциональна её степени. Это естественный результат: если у вас в какой-то узел приходит 5 труб, а в какой-то всего 2, то вероятность оказаться в узле с 5 трубами выше.
Теперь мы можем перейти к одной из самых известных задач на графах — PageRank.
PageRank
Это алгоритм, изначально созданный для ранжирования веб-страниц. Он моделирует поведение случайного пользователя, который случайным образом переходит по ссылкам на страницах.
Представьте себе огромную библиотеку, где миллиарды сайтов ссылаются друг на друга. Как в интернете найти действительно полезную и авторитетную информацию? В 1998 году два аспиранта Стэнфордского университета — Ларри Пейдж и Сергей Брин — предложили простую идею: давайте измерять «важность» страницы по тому, сколько раз на неё ссылаются другие страницы.
И не просто по количеству ссылок, а с учётом того, насколько сами эти страницы авторитетны. Так появился PageRank — алгоритм, положивший начало поисковой системе Google.
Грубо говоря, они применили принцип, распространённый в научном сообществе: у учёных и по сей день одной из важных метрик считается цитируемость — индекс Хирша. Если вы пишете крутые статьи — значит, на вас часто будут ссылаться.
Рассматриваем интернет как ориентированный граф: вершины — страницы сайтов, рёбра — ссылки между ними. Дальше вводим вероятность перехода по ссылкам с текущей страницы . То есть с вероятностью человек перейдёт по ссылкам, а с вероятностью перейдёт на другую случайную страницу. Это сделано для того, чтобы избежать тупиков и периодичности. Как же это связано с диффузией?
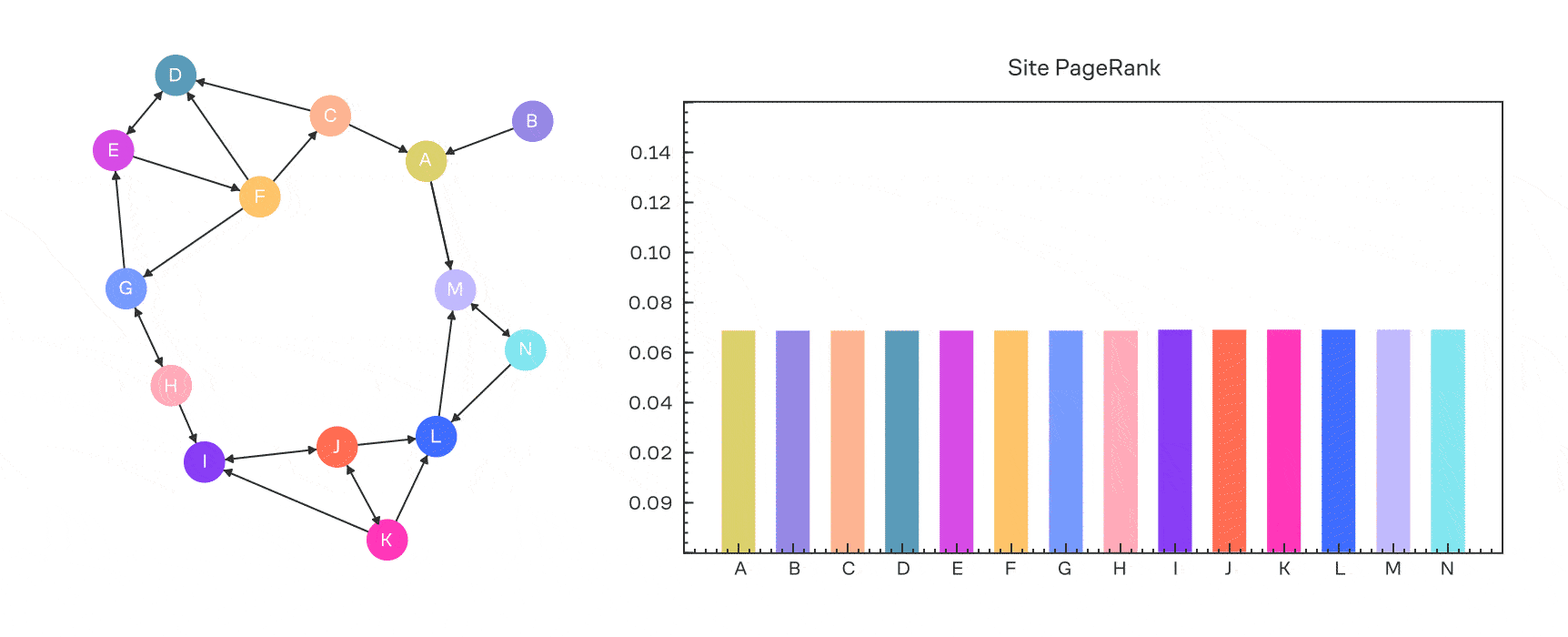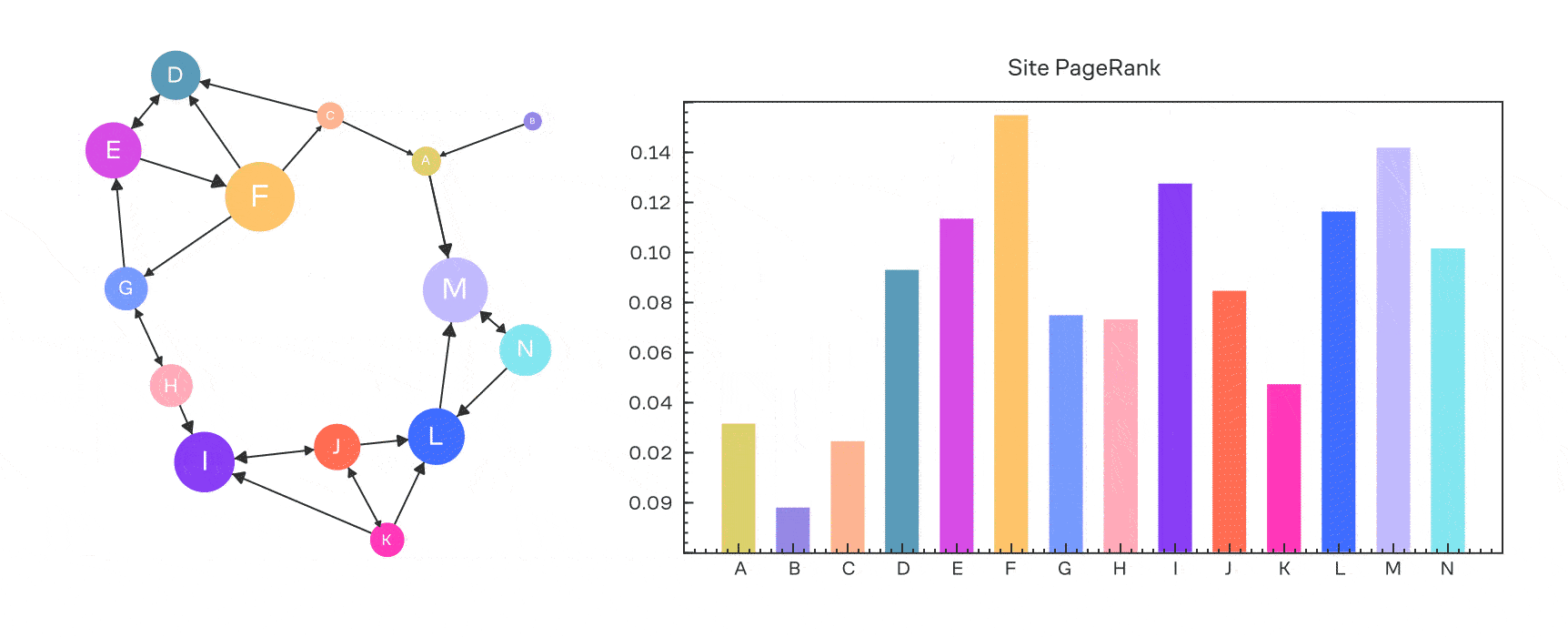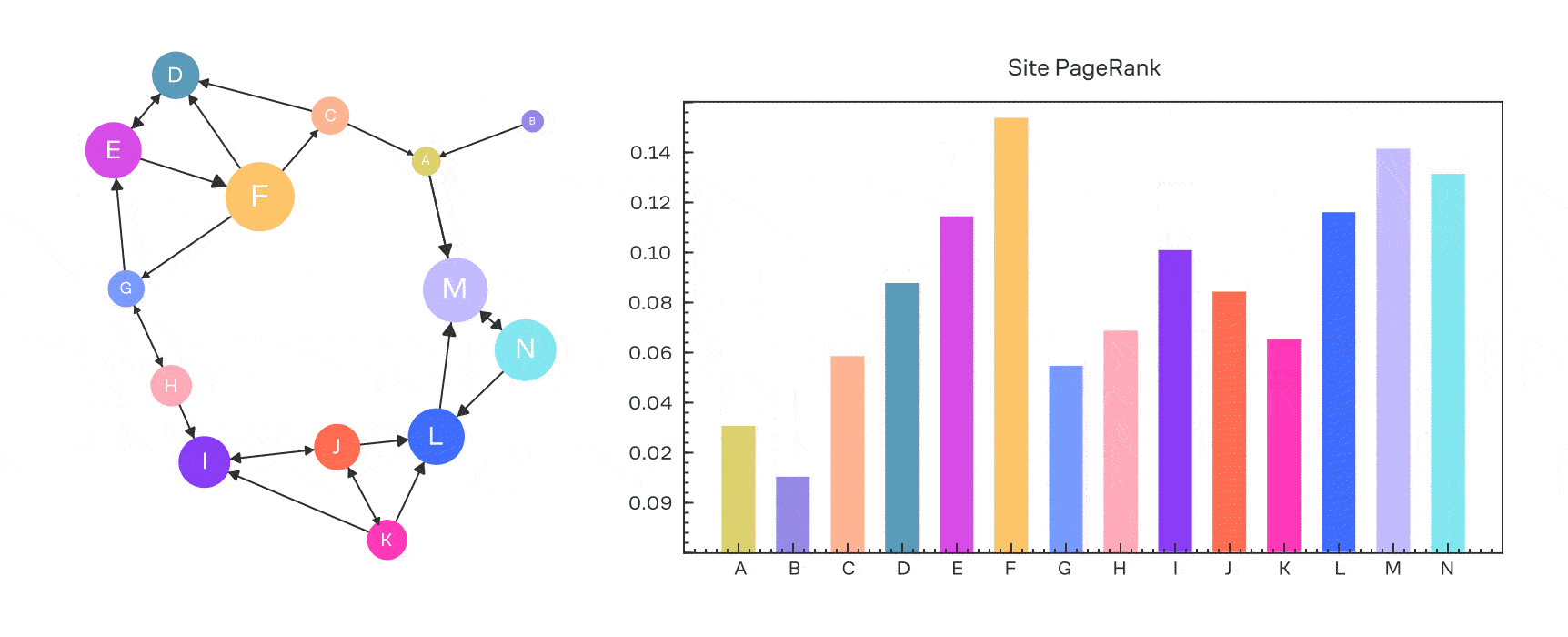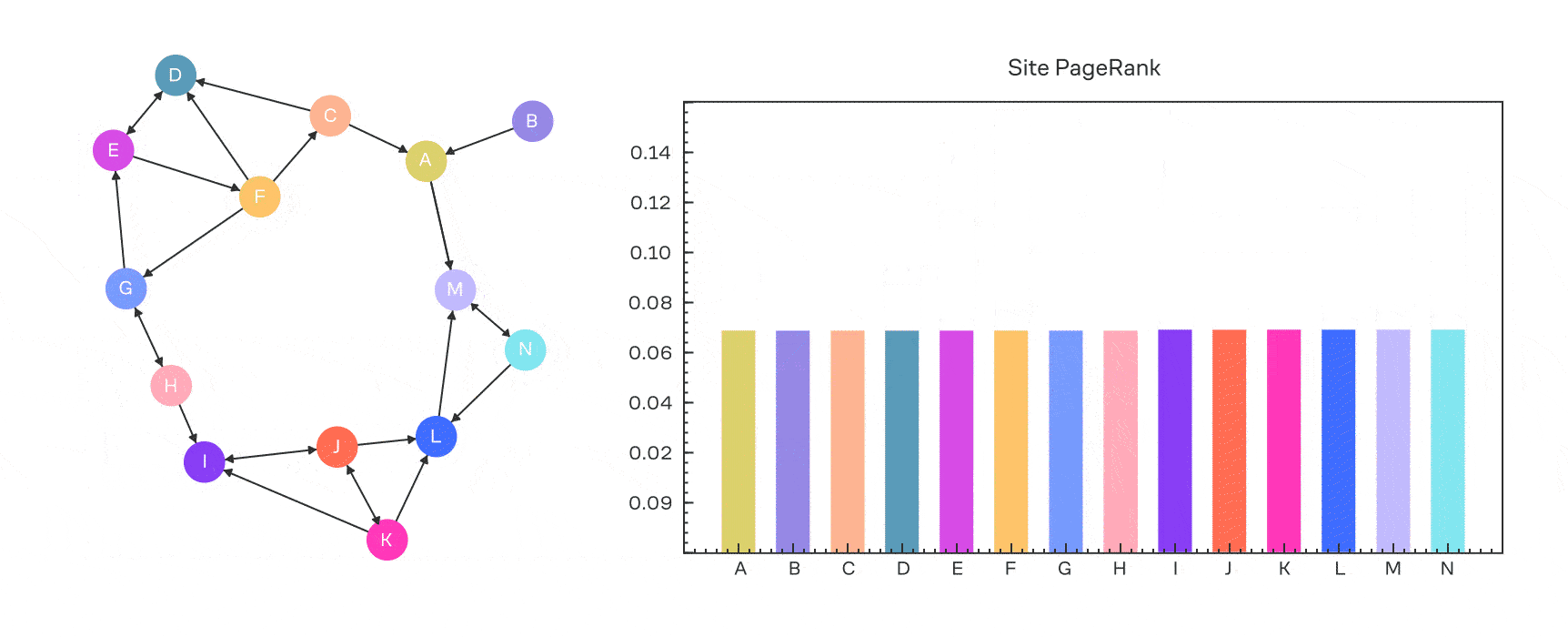
Выше мы получали для вектор-столбца сигнала в задаче диффузии. Давайте применим это к вектор-строке вероятности: .
Вспомним, что в PageRank у нас есть . Можно ли это учесть? Вполне!
где — вектор перехода на случайную страницу; . Если он равномерный (то есть все его значения равны), то получим обычный PageRank.
Но это не обязательно, мы можем сделать его и персонализированным (какие-то значения больше других). Например, пользователь не перейдёт на случайный сайт, а предпочтёт вернуться на сайты с красивым дизайном. Такая модификация называется Personalized PageRank.
Решим задачу PageRank в пределе стационарного распределения :
В последнем действии есть важный нюанс: мы считаем, что обратная матрица существует. Что для этого надо?
- Если у вершины нет исходящих рёбер, то строка в не определена. Надо это исправить, например заменив пустую строку на .
Перепишем задачу PageRank через лапласиан, чтобы увидеть её связь с процессами сглаживания на графе.
Ключ — связь матрицы переходов и нормализованного лапласиана случайного блуждания . Подставим в стационарное уравнение:
- Исходное уравнение:
- Подстановка и группировка:
- Итоговая линейная система:
Эта запись раскрывает PageRank как задачу сглаживания с «якорем»:
- член отвечает за сглаживание (делает значение узла ближе к среднему по соседям);
- член — это «якорь», который тянет решение к вектору телепортации .
Чем выше , тем сильнее влияние структуры графа (сглаживание) и слабее влияние «якоря». Формула с обратной матрицей из предыдущего вывода — это явное решение этой системы.
Уравнение PageRank можно переписать в ещё более компактной форме. Если ввести параметр , то линейная система примет вид:
Эта запись подчёркивает роль как коэффициента гладкостной регуляризации на графе. Она показывает, что итоговый ранг — это некий компромисс между близостью к исходному вектору (за это отвечает ) и гладкостью решения на графе (за это отвечает ).
Столбцовая запись и симметричная форма
В этом параграфе мы использовали строчную запись: — строковый вектор, , а — построчно-стохастическая матрица переходов.
Столбцовая формулировка
Эквивалентная запись со столбцовыми векторами (часто встречается в литературе):
Это даёт линейную систему:
Для узлов без исходящих рёбер («висячие» узлы) соответствующие строки нужно корректировать (например, заменять вектором ), чтобы система была корректно определена.
Симметричная СЛАУ для неориентированных графов
Если граф неориентированный (), то систему можно сделать симметричной. Подстановкой получаем симметричную положительно определённую систему:
что удобно для численных решателей (метод сопряжённых градиентов, разложение Холецкого и другие).
Мы увидели, как PageRank использует диффузионный процесс для распространения «важности» по графу.
Оказывается, этот же мощный механизм можно применить и для совершенно другой задачи — полунадзорной классификации. Вместо того чтобы распространять ранг, мы будем распространять известные метки классов от немногих размеченных вершин ко всем остальным. Этот алгоритм называется Label Propagation.
Label Propagation
Это один из базовых алгоритмов полунадзорного обучения на графах — подхода, при котором для обучения модели используется смесь размеченных и неразмеченных данных.
В нашем случае известные метки распространяются по рёбрам на соседние вершины — как краска, падающая в воду и постепенно окрашивающая всё вокруг. Со временем распределения меток в узлах выравниваются, и вершины с изначально неизвестной категорией получают метку в зависимости от того, какие классы преобладают среди их соседей.
Допустим, что есть граф, в котором у части вершин мы знаем их метки, а у части — нет. Обозначим матрицу исходных меток . Для каждой размеченной вершины соответствующая ей строка в будет вектором из нулей, где на позиции, соответствующей номеру класса, стоит единица (такие векторы называются one-hot). Строки для неразмеченных вершин будут состоять из одних нулей.
Сделаем ещё одну матрицу , в строках которой будет лежать распределение вероятности меток для каждой вершины. Её и будем искать. Запишем задачу через процесс диффузии:
Матрицу инициализируем Не будем подробно останавливаться на расписывании решения, поскольку оно аналогично предыдущему. Отметим, что здесь также нужно перейти к пределу, и тогда можно получить:
Обратите внимание на поразительное сходство этой формулы с решением для PageRank. В обоих случаях ядром является одна и та же матричная структура , что подчёркивает единство лежащего в их основе диффузионного процесса.
Геометрия через диффузию
Мы уже увидели, что и диффузия, и PageRank используют одну и ту же динамику по графу:
- непрерывную, через тепловой оператор (heat kernel);
- дискретную — через матрицу переходов (где связан с .
Но на практике часто нужны не только сглаживание и фильтрация сигнала, а компактные координаты вершин, в которых обычное евклидово расстояние отражает близость по сети.
Диффузионные карты (англ. Diffusion Maps) как раз это и делают: берут оператор диффузии и строят эмбеддинг низкой размерности, где расстояния между точками аппроксимируют вероятность добраться друг до друга за шагов случайного блуждания (так называемую диффузионную дистанцию). Это удобно для визуализации, кластеризации и поиска скрытой геометрии данных — особенно когда прямые расстояния плохо передают структуру графа/многообразия.
Представьте себе парк с дорожками, которые извиваются между деревьев. Люди могут ходить только по этим дорожкам. Если смотреть на парк сверху, то расстояния между людьми можно измерить «по прямой» — так, как летел бы самолет. Но на самом деле люди могут добраться друг до друга только вдоль дорожек, и прямое расстояние не отражает их истинную «близость».
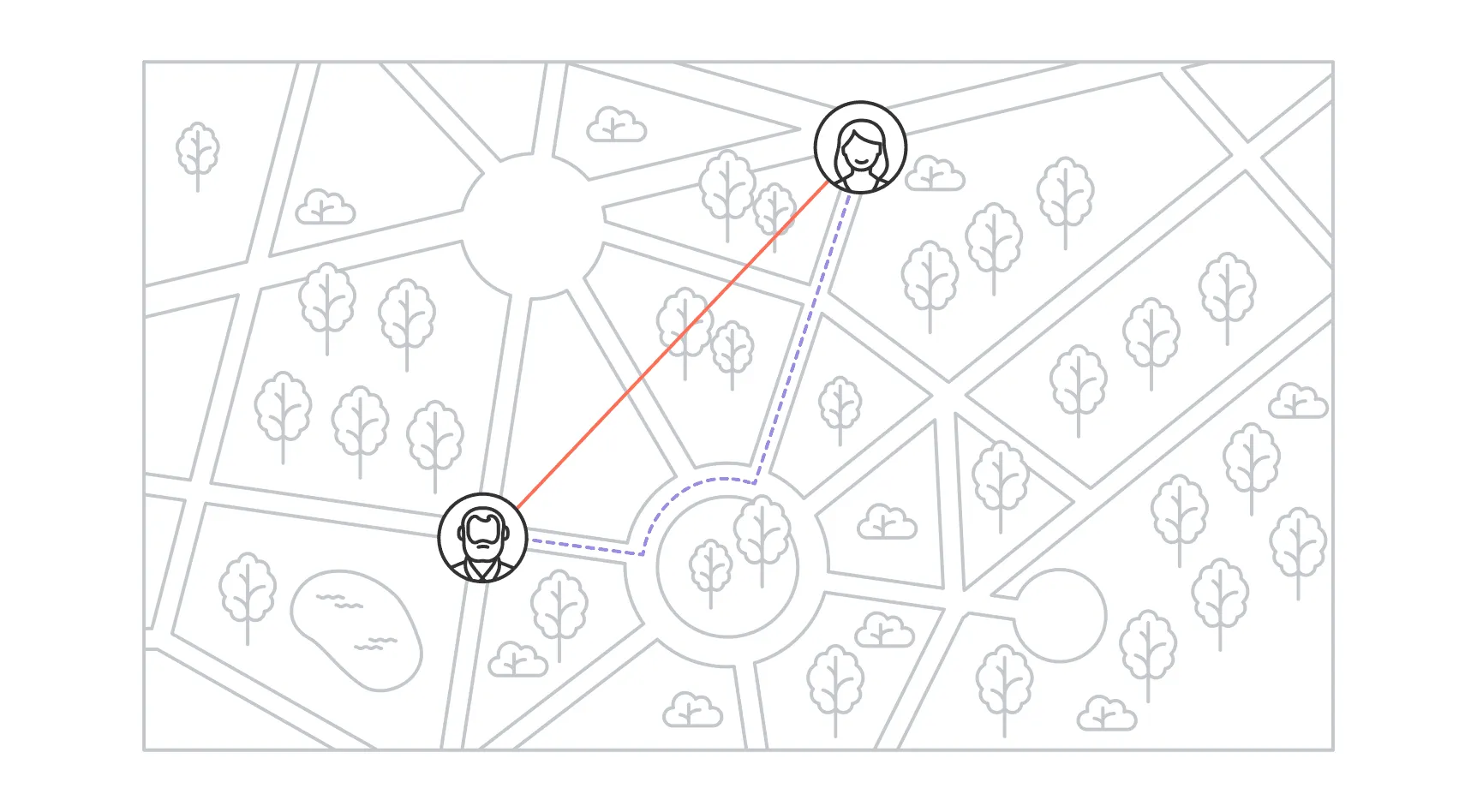
Идею диффузионных карт можно визуализировать так: представьте, что мы запускаем маленького муравья, который бежит по дорожкам (графу) случайным образом. Мы смотрим, насколько быстро он может добраться из одной точки в другую, и эти «времена добегания» формируют новую меру расстояния. Затем мы «сворачиваем» карту парка так, чтобы эти времена (а не прямые линейные расстояния) сохранялись. Ещё одна аналогия: как будто муравей ползет по коктейльной трубочке, а мы по спирали разворачиваем её в линию.
В спектральных терминах это эквивалентно применению низкочастотного фильтра, который подавляет резкие изменения между соседними вершинами и усиливает плавные, согласованные паттерны.
Более формально это делается через спектральное разложение графового лапласиана. Пусть
Тогда координаты Diffusion Maps масштаба задаются как
и евклидово расстояние аппроксимирует диффузионную дистанцию между вершинами и . Параметр — это «масштаб обзора»: малые подчеркивают локальную структуру, большие — более глобальные паттерны. Заметим, что множители играют роль низкочастотного фильтра: чем больше , тем сильнее подавляется соответствующая компонентa.
Эта связь между динамикой диффузии и частотными компонентами приводит нас к более общей идее — графовых фильтров, которые позволяют избирательно усиливать или подавлять определённые частоты сигнала на графе. Именно через такие фильтры строятся многие современные алгоритмы, включая графовые свёрточные сети.
Фильтры
В классическом машинном обучении и обработке сигналов фильтры помогают выделять важные частоты и подавлять шум. Но как фильтровать данные, заданные не на регулярной решётке (например, изображении), а на графе — структуре с произвольной связностью?
Представьте социальную сеть, где у каждого пользователя есть мнение по какому-то вопросу (сигнал на вершинах). Часть мнений шумная или экстремальная. Задача — получить сглаженную картину по сообществам, подавив шум, но не размыв границы между группами.
Графовый фильтр — это как раз такой инструмент: он усредняет сигнал по соседям в графе (друзьям в сети) с регулируемой интенсивностью и локальностью. Слабое сглаживание подавляет одиночные выбросы, а более сильное выявляет устойчивые тенденции внутри сообществ, сохраняя макроструктуру сети.
Пара слов о локальности. Она означает, что влияние фильтра должно распространяться не на весь граф, а только на окрестность вершины (ближайшие соседи, соседи через одного). Это важно для вычислительной эффективности, и кажется логичным, что изменение сигнала в одной вершине должно влиять только на близлежащие вершины, а не на весь граф.
Для построения эффективных фильтров нам снова понадобится нормализованный симметричный лапласиан, который мы уже вводили ранее:
Он обладает парой удобных свойств:
- Он симметричен.
- Все его собственные значения лежат в диапазоне , а максимум достигается тогда и только тогда, когда граф
двудольный, — как мы уже знаем, это граф, вершины которого можно разбить на две доли так, что рёбра соединяют только вершины из разных долей.
Спектральные графовые фильтры
Общая идея графового фильтра — это операция, которая изменяет спектр сигнала на графе. Мы можем усилить или ослабить определённые частоты (собственные значения ), чтобы, например, сгладить сигнал (подавить высокие частоты) или, наоборот, выделить резкие изменения (усилить высокие частоты).
Формально это реализуется через спектральное разложение лапласиана . Графовый фильтр — это оператор , который в спектральном представлении действует как функция на собственные значения:
Здесь — это диагональная матрица, где каждый элемент — это результат применения функции к соответствующему собственному значению, а — параметры, определяющие форму фильтра (например, коэффициенты полинома).
Применение такого фильтра к сигналу выглядит как:
Этот подход красив и понятен:
- Анализ. Переводим сигнал в спектральное представление ().
- Фильтрация. Умножаем на коэффициенты фильтра ().
- Синтез. Возвращаем сигнал обратно ().
То есть для применения фильтра требуется привести матрицу к диагональному виду. Для больших графов этот процесс будет долгим: в общем случае приведение матрицы к диагональному виду имеет асимптотику для матрицы размером . Можно ли как-нибудь обойтись без этого?
Полиномиальные фильтры
Оказывается, что да. Рассмотрим полиномиальный фильтр. То есть такой, где — полином степени :
Это можно переписать в матричном виде:
а применение фильтра сводится к:
Это гораздо проще применять, поскольку нам не требуется приводить лапласиан к диагональному виду. Степень полинома при этом определяет количество соседей, которые участвуют в формировании нового пространства. Из-за этого полиномиальный фильтр получается локальным.
Фильтры Чебышёва и GCN
Чтобы сделать полиномиальные фильтры более гибкими и численно устойчивыми, вместо обычных степеней часто используют базис из многочленов Чебышёва . Их главное преимущество — эффективное вычисление через рекуррентную формулу:
Подробнее о многочленах Чебышёва
Многочлены Чебышёва первого рода обладают рядом уникальных свойств, которые делают их полезными для аппроксимации функций:
- Минимальное отклонение от нуля. Многочлен степени со старшим коэффициентом меньше всего отклоняется от нуля на отрезке .
- Чётность и нечётность. Многочлены чётных степеней являются чётными функциями (содержат только чётные степени ), а нечётных — нечётными. Для лучшего понимания приведем здесь и
Легко заметить, что и .
- Ортогональность. Они образуют систему ортогональных многочленов, что важно для численной стабильности.
Чтобы применить их к графу, спектр лапласиана сначала нужно уместить в отрезок , на котором эти многочлены обладают наилучшими свойствами:
где — максимальное собственное значение .
Тогда фильтр Чебышёва степени определяется как:
При этом мы можем воспользоваться рекуррентным соотношением выше, чтобы посчитать результат применения такого фильтра без необходимости приведения матрицы к диагональному виду.
Иллюстрация графовой свёрточной сети.
Именно этот подход лежит в основе графовых свёрточных сетей (англ. Graph Convolutional Network, GCN). Идея GCN — взять самый простой, но нетривиальный локальный фильтр Чебышёва () и сделать его обучаемым.
Всё, что требуется, — взять и приблизить : действие такого фильтра на сигнал можно свести к выражению с двумя параметрами, и . Чтобы сократить их до одного и получить каноническую формулу GCN, используется трюк с перепараметризацией.
Положим, . Это ограничение позволяет связать два параметра в один и приводит к очень изящному результату. Подставим это в одну из промежуточных форм фильтра:
Раскрыв скобки, получаем уже чистую агрегацию соседей:
Здесь возникает важный нюанс. В такой форме оператор при применении к вектору усредняет значения только по соседям вершины, полностью игнорируя исходное значение в самой вершине. На практике это часто приводит к потере информации.
Чтобы решить эту проблему, в GCN используется простой, но мощный трюк ренормализации: сначала добавляют «петли» (англ. self-loops), а уже потом нормализуют:
Это приводит к финальной, канонической форме слоя GCN:
Вот как теперь работает эта операция:
- добавляет вклад самой вершины (self-loop),
- агрегирует информацию от соседей и самой вершины в устойчивом масштабе,
- умножение на делает фильтр обучаемым.
Теперь у нас в скалярной постановке остался всего один обучаемый параметр на слой, а сама операция интуитивно понятна: она усредняет вектор признаков вершины с векторами её соседей, не теряя собственный сигнал.
На практике GCN работают не с одним сигналом, а с матрицей признаков , где каждая строка — это вектор признаков для одной вершины. Тогда формула обобщается:
Где:
- — матрица входных признаков;
- — выходные признаки;
- — обучаемая матрица весов слоя нейросети (в многоканальном случае она заменяет скаляр ).
Эта операция, по сути, для каждой вершины усредняет её вектор признаков с признаками соседей (и собственной вершины), создавая новое, обогащённое представление.
ARMA-фильтры
Полиномиальные фильтры, включая фильтры Чебышёва, отлично подходят для создания гладких, в основном низкочастотных (сглаживающих) фильтров. Но что делать, если нам нужна более сложная частотная характеристика — например, выделить определённую полосу частот, подавив и низкие, и высокие?
Для таких задач используют ARMA-фильтры (англ. AutoRegressive Moving Average, авторегрессионный фильтр скользящей средней), пришедшие из анализа временных рядов. Их ключевое отличие в том, что функция фильтра задаётся не полиномом, а рациональной функцией (отношением двух полиномов). В спектральной области (для , где ) функция задаётся как:
В операторной форме это:
Рациональная форма позволяет строить избирательные, в том числе полосовые и режекторные, фильтры с меньшим порядком, чем у чисто полиномиальных аппроксимаций. Это полезно, когда требуется выделить средние масштабы структуры и подавить и слишком локальные всплески, и слишком глобальные тренды.
Например, в транспортной сети такой фильтр может помочь подчеркнуть районные паттерны трафика, приглушив как шум отдельных перекрёстков (высокие частоты), так и общефоновую нагрузку города (низкие частоты).
Что следует учитывать?
- Вычисления. Реализация сводится к решению линейной системы или итерационным схемам, а это дороже, чем простая полиномиальная свёртка, например.
- Устойчивость. Для численной устойчивости коэффициенты выбирают так, чтобы знаменатель не обращался в ноль на .
- Выбор. Если важны скорость и простота, берут полиномиальные/чебышёвские фильтры. Если нужна острая частотная селективность — выигрывает ARMA.
Всё, что мы обсуждали до этого, — спектр, диффузию и графовые фильтры — можно рассматривать как способы преобразования исходных сигналов на графе в более удобное представление, подчёркивающее нужные свойства структуры.
Однако фильтры в первую очередь работают с сигналами на фиксированном графе.
Если же задача — сравнивать разные графы между собой или искать похожие вершины или структуры в большом наборе графов, нам нужны другие инструменты.
Здесь на сцену выходят два подхода:
Графовые ядра— позволяют ввести меру сходства между графами или их элементами, что особенно полезно для алгоритмов, основанных на матрицах сходства (например, SVM).Графовые эмбеддинги— представляют вершины, подграфы или целые графы в виде векторов фиксированной размерности, чтобы применять к ним стандартные методы машинного обучения.
Мы рассмотрим эти подходы в следующем параграфе, а пока советуем пройти квиз, чтобы закрепить прочитанный материал.



