Когда мы работаем с графами, часто нужно понимать, насколько похожи два графа друг на друга. Например:
- Похожи ли две молекулы по структуре?
- Похожи ли два человека в соцсети по их связям?
- Можно ли предсказать, появится ли новое соединение в молекуле, если у нас есть похожие?
Чтобы это делать, нужно уметь сравнивать графы. Для обычных векторов достаточно просто сравнить похожесть. Можно, например, посчитать косинус угла между ними, тем самым оценив, направлены они в одну сторону или в разные.
А как быть с графами? Тут дела обстоят сложнее, но существует два мощных подхода, которые мы последовательно рассмотрим: ядра (англ. kernels) и эмбеддинги (англ. embeddings).
Затем покажем, как на их основе решать практические задачи: кластеризацию (алгоритм Ng-Jordan-Weiss), выделение признаков для табличных ML-моделей, а также быстрый поиск похожих объектов (NSW/HNSW).
Начнём с ядер.
Графовые ядра
Это функции, которые измеряют сходство между графами, не переводя их в векторы явно. В этом разделе мы поговорим о трёх ключевых типах ядер:
- Ядро на случайных блужданиях (англ. Random Walk kernel) — оно сравнивает графы по набору случайных путей в них.
- Ядро на кратчайших путях (англ. Shortest-Path kernel) — оно использует расстояния между парами вершин.
- Ядро Weisfeiler-Lehman — это мощный мощный метод, основанный на итеративном сравнении локальных окрестностей вершин.
Ядро на случайных блужданиях
Возьмем два графа. В каждом из них запустим случайное блуждание — представьте пьяницу, который случайно гуляет по улицам-рёбрам города — и посмотрим, как часто встречаются одинаковые «пути».
Как ядро пьяницы записывается формулой? Для блужданий максимальной длины :
где — коэффициент затухания (чем длиннее путь, тем менее он для нас важен), — вероятность пройти путь длиной в графе 1, начиная из вершины . Этот показатель косвенно отражает структуру окрестности вершины.
Если графы помечены (то есть вершины и/или рёбра имеют метки/атрибуты — тип атома, цвет, роль пользователя, тип связи и т. п.), совпадение путей обычно считают по последовательностям этих меток или через небольшое «ядро на метках». Если нет — по самим последовательностям вершин. Для сопоставимости значений часто используют нормировку:
У данного ядра есть два важных недостатка:
- Оно долго считается на больших графах, поскольку требуется перебрать очень много путей (эквивалентная матричная форма приводит к работе с произведением графов размера ).
- Случайные рёбра и топтание на месте (то есть частые возвраты туда-обратно по одному ребру), будут сильно портить результат. На практике это смягчают малым и — запретом мгновенного возврата или переходом к более устойчивым ядрам.
Из-за этих ограничений случайные блуждания в чистом виде используются редко. Однако сама идея исследовать граф через пути легла в основу более современных и эффективных методов, таких как эмбеддинги DeepWalk и Node2Vec, которые мы рассмотрим далее. А пока перейдём к более простому и устойчивому подходу — ядру на кратчайших путях.
Ядро на кратчайших путях
Давайте вместо случайных путей рассматривать кратчайшие. Интуиция такая: если в двух графах много пар узлов с одинаковыми расстояниями, то они похожи.
Пусть — кратчайшее расстояние между вершинами и . Тогда ядро можно записать так:
где обозначают индикатор (также известный как скобка Айверсона), то есть функцию, которая принимает , если условие внутри выполнено, и — если нет. Суммы берутся по неупорядоченным парам , чтобы не считать каждую пару дважды.
Эту же идею удобно переписать через гистограммы расстояний. Для каждого графа мы можем составить функцию , которая подсчитывает, сколько пар вершин находится на расстоянии друг от друга:
Здесь символ означает мощность множества (число его элементов). Для чисел — это модуль, но здесь аргументом является множество.
Тогда формула ядра превращается в простое скалярное произведение этих гистограмм, в некое ядро на кратчайших путях:
Такой взгляд показывает, что мы, по сути, превращаем каждый граф в вектор (гистограмму расстояний), а затем измеряем их сходство через скалярное произведение.
💡Если графы помеченные (вершины/рёбра имеют некие атрибуты), то сравнение можно ужесточить: учитывать только пары с совпадающими метками или добавить «ядро на метках» внутри индикатора.
Для взвешенных графов часто сравнивают не точное равенство расстояний, а близость — например, через или бининг расстояний.
Такое ядро работает быстрее, но содержит меньше информации о структуре, скажем, игнорируем узор окрестностей (сколько и какие соседи, их метки и т. д.). Для более тонкого учёта окружения вершин применяют подход Weisfeiler-Lehman.
Ядро Weisfeiler-Lehman
Это самое сложное ядро, которое мы разберём. Вот его алгоритм:
- Даём метку каждой вершине (по типу атома, по цвету и т. д.).
- Повторяем N раз (обычно 2–5):
- Для каждой вершины собираем метки всех соседей.
- Склеиваем метки .
- Хешируем полученную строку (присваиваем новую метку).
- Считаем, сколько раз одинаковые метки появились в обоих графах.
Формулой это можно записать так:
где — гистограмма меток на шаге , — скалярное произведение.
Интуиция за этим алгоритмом такая: если два узла находятся в похожем окружении (такие же соседи и структура), они получат одинаковые метки. А чем больше совпадений в метках и их истории, тем более похожи графы.
В математике существует тест на изоморфизм. Изоморфизм — логико-математическое понятие, выражающее одинаковость строения (структуры) систем (процессов, конструкций). Графы считаются изоморфными в том случае, если они имеют одинаковую структуру, но различный внешний вид.
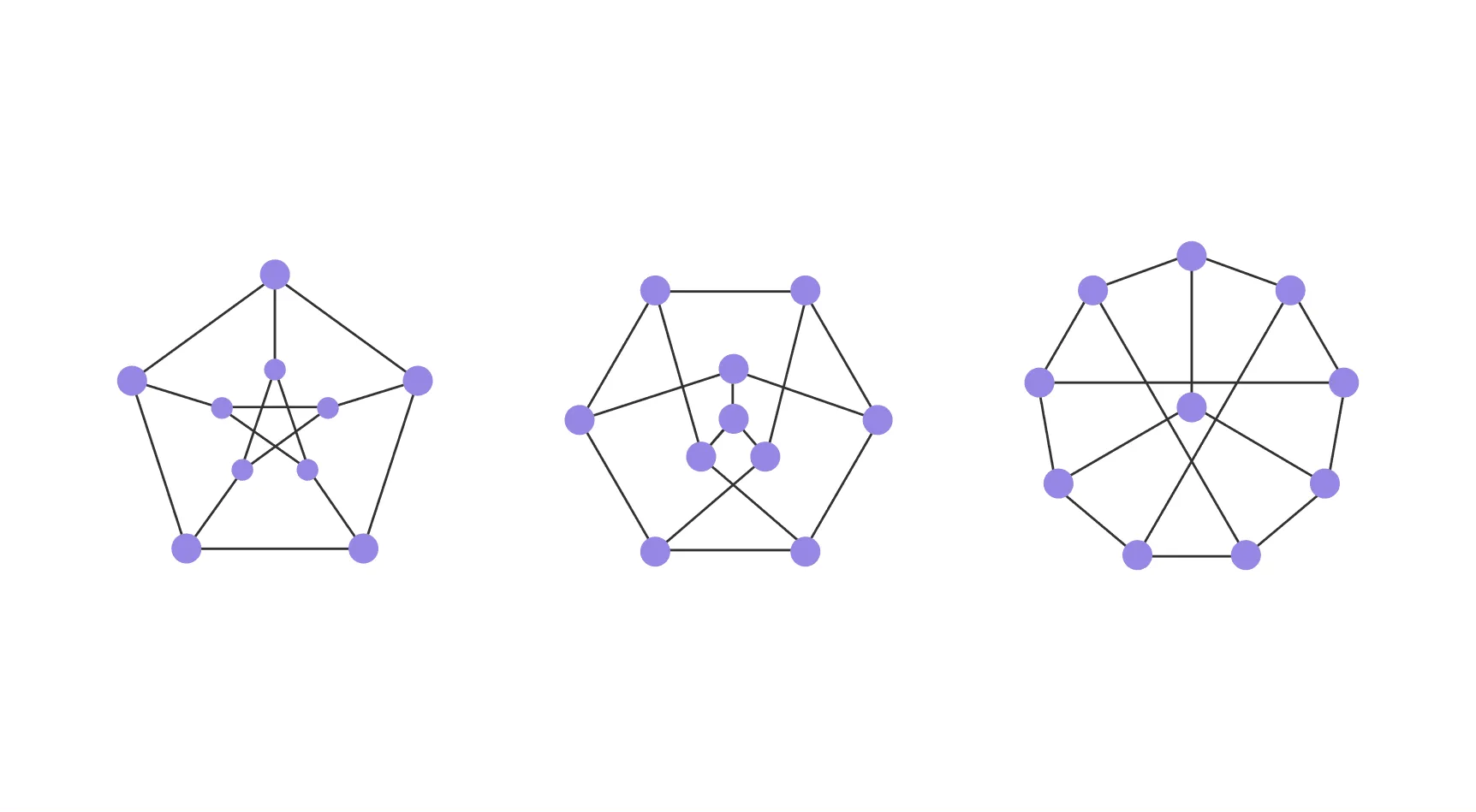
Пример изоморфных графов.
Weisfeiler-Lehman основан на тесте изоморфизма графов: если два графа неразличимы этим методом, то, возможно, они изоморфны (структурно одинаковы). Из этого вытекает, что это ядро ещё и удобный инструмент проверки структурной эквивалентности.
Таким образом, ядра позволяют измерять степень сходства графов, неявно задавая пространство признаков.
Однако иногда полезнее явно построить это пространство — представить вершины или целые графы в виде числовых векторов. Такой подход называется эмбеддингами графов.
Эмбеддинги графов
Эмбеддинг — это способ превратить объект (например, слова в тексте, вершины или целый граф) в вектор чисел, с которым удобно работать в машинном обучении.
Этот подход нужен потому, что классические алгоритмы машинного обучения, такие как логистическая регрессия, бустинг и другие, не умеют работать с графами напрямую. Они ожидают на вход стандартную таблицу признаков. В NLP-задачах похожие эмбеддинги получают слова, встречающиеся в схожих контекстах. А как в графах?
Основной принцип такой: вершины, имеющие схожее структурное положение в графе, должны получить близкие векторные представления.
Рассмотрим на примере графа социальной сети. Пусть вершины — люди, а рёбра — наличие друг друга в списке друзей. Если у двух людей много общих друзей, они занимают похожее место в социальной структуре. Следовательно, хороший алгоритм построения эмбеддингов должен поместить их векторы близко друг к другу в признаковом пространстве.
Представим двух людей, которые сначала учились в одном классе, а потом в одной группе в университете. Логично, что с точки зрения социального контекста они будут похожими, и их эмбеддинги это отразят.
Рассмотрим несколько методов создания эмбеддингов:
- DeepWalk, использующий случайные блуждания;
- Node2Vec, который делает эти блуждания более управляемыми;
- Graph2Vec, обобщающий идею на целые графы.
DeepWalk
Выше уже неоднократно говорили про случайные блуждания. Давайте и здесь ими воспользуемся!
Алгоритм будет такой:
- Запускаем из каждой вершины несколько случайных прогулок (например, длиной 10–80 шагов). Каждая прогулка — это «предложение» из вершин, или последовательность узлов.
- Накопив много таких последовательностей, получаем «текст» на алфавите вершин.
- На этом сгенерированном корпусе предложений обучается модель Word2Vec (CBOW или Skip-Gram с negative sampling). Это популярная нейросетевая модель из NLP, которая получает векторы для слов, предсказывая их контекст в окне размера .
Узлы графа «слова»,
последовательности из случайных блужданий «предложения».
Как видите, идея DeepWalk заключается в использовании хорошо зарекомендовавшего себя алгоритма с модификациями: узлы графа — это слова, а случайные блуждания — это предложения.
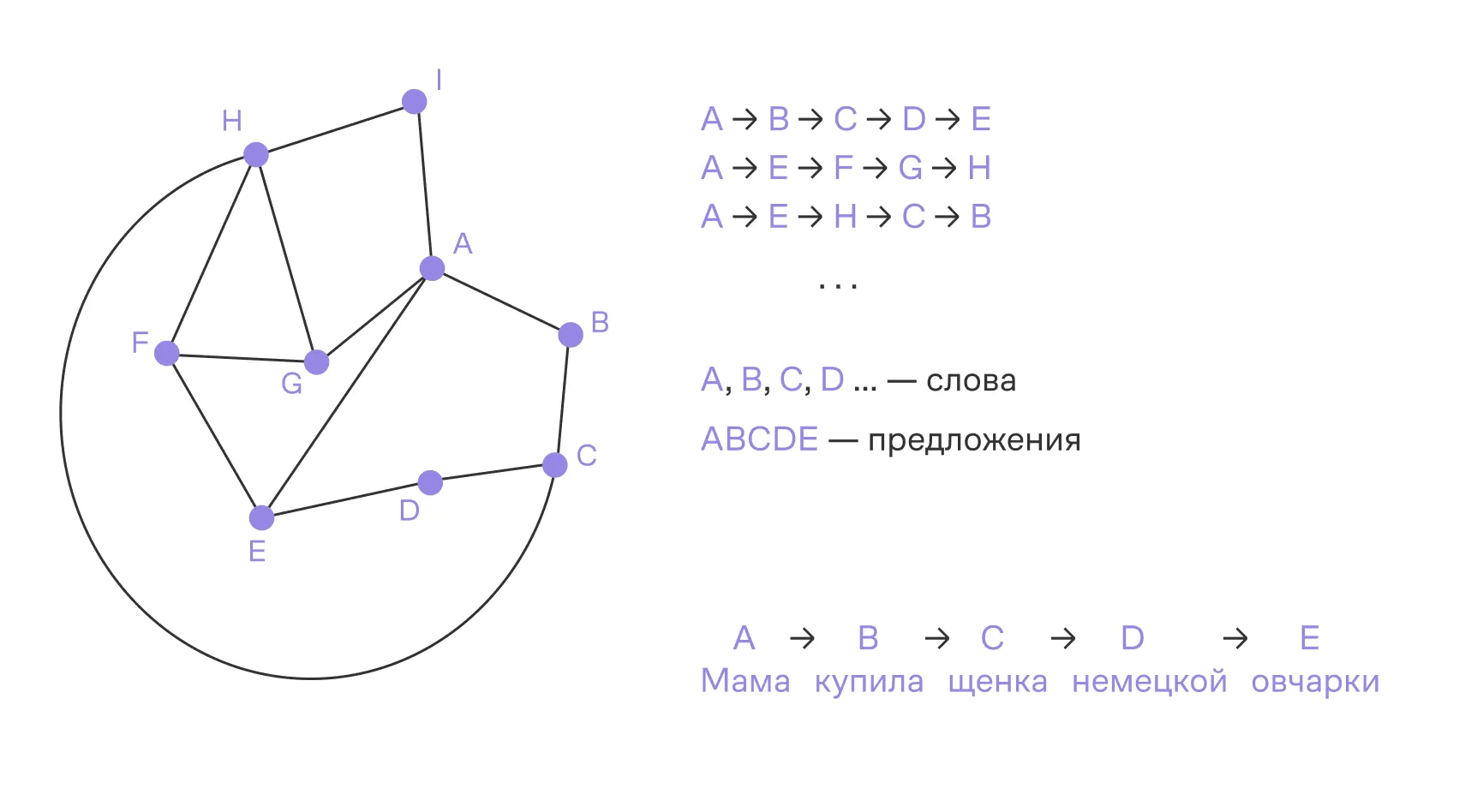
Пример одного случайного блуждания: A → B → D → C → E. Таких нужно собрать много, после чего можно приступать к обучению Word2Vec.
В итоге мы получим матрицу эмбеддингов : у каждой вершины есть -мерный вектор. Вершины, которые часто встречаются вместе в коротких прогулках, то есть находятся в похожем сетевом окружении, получают близкие векторы. Эти эмбеддинги удобно использовать для:
- классификации вершин,
- предсказания рёбер (англ. link prediction),
- поиска похожих узлов и кластеризации (косинусное сходство и т. п.).
Из практических настроек достаточно задать длину прогулки , число прогулок с каждой вершины , размер окна , размерность и число негативных примеров при обучении.
Node2Vec
Разобранный выше алгоритм работает неплохо, но он гуляет случайно и не может отличить разные типы соседей: близких соседей от узлов, которые находятся в одной «роли». Тем не менее зачастую нам хочется сфокусироваться на локальной или на глобальной структуре.
Здесь стоит вспомнить про алгоритмы обхода в глубину (англ. Depth-First Search, DFS) и обхода в ширину (англ. Breadth-First Search, BFS). Возможно ли мотивы из этих алгоритмов применить для подсчета эмбеддингов?
Да, давайте запустим случайную прогулку с модификацией: на каждом шаге выбираем следующую вершину не просто равновероятно из соседей, а с весами, зависящими от того, откуда мы пришли.
Пусть теперь вероятность перехода из узла в узел зависит от предыдущего узла , из которого мы пришли в . Эта вероятность определяется весом:
где — вес ребра между узлами и (в общем случае он необязательно равен ), — bias, или смещение, который рассчитывается следующим образом:
где — кратчайшее расстояние между предыдущим узлом и узлом .
У нас появилось две «ручки», которые можно крутить:
- — параметр возврата:
- : мы избегаем возврата назад (поскольку будет меньше 1)
- : мы поощряем возврат назад (поскольку будет больше 1)
- — параметр исследования:
- : алгоритм напоминает BFS и как бы фокусируется на локальных связях
- алгоритм напоминает DFS и стремится уйти как можно дальше
После построения «предложений» модифицированной версией DeepWalk [обучают](https://education.yandex.ru/handbook/ml/article/nejroseti-dlya-raboty-s-posledovatelnostyami#:~:text=предложили две стратегии%3A-,Skip-gram,-и CBOW (Сontinuous) Word2Vec на графе.
Graph2Vec
Как быть, если мы хотим шагнуть вперед и отойти от вершин к целым графам? Возьмем алгоритм Graph2Vec. Если Node2Vec учит векторы для узлов, то Graph2Vec делает это для целых графов.
Идея Graph2Vec заимствована из модели doc2vec в NLP: каждый граф рассматривается как «документ», а его локальные подструктуры — как «слова». Цель — обучить для всего графа единый вектор, который будет хорошо предсказывать, какие «слова» (подструктуры) в нём содержатся.
Как мы будем это делать:
- Запускаем для каждого графа алгоритм Weisfeiler-Lehman: на каждом шаге вершина переобозначается функцией от своей метки и мультимножества меток соседей, 2–5 итераций дают устойчивые «подписи» локальных окрестностей.
- Обучаем модель Skip-Gram, максимизируя вероятность:
где:
- — эмбеддинг графа;
- — эмбеддинг подструктуры;
- — множество всех возможных подструктур.
На практике эту сумму приближают методом отрицательных примеров (negative sampling): вместо суммирования по всем берут небольшое случайное подмножество «негативных подструктур».
В чём преимущество? Теперь мы можем работать с целыми графами — у нас на руках компактный вектор , с которым можно решать привычные задачи: классифицировать целые графы (например, токсичность молекул), искать похожие графы по косинусной близости, визуализировать коллекции графов. Тот же принцип работает и на уровне вершин (Node2Vec).
Логичный следующий шаг — группировать эти векторы. Далее мы разберём спектральную кластеризацию (Ng-Jordan-Weiss) и покажем, как она выявляет сообщества, опираясь на графовую структуру. Практически полезно L2-нормализовать эмбеддинги и подобрать разумную размерность (часто 32–256), чтобы сбалансировать качество и устойчивость. А для быстрого поиска похожих графов в больших коллекциях удобно использовать приближённые индексы ближайших соседей (например, HNSW/FAISS).
Кластеризация и важность узлов в графах
В этой части узнаем, что даже без использования графовых нейросетей (GNN) можно извлекать информативные признаки из структуры графа и успешно применять их в табличных ML-моделях.
Один из ярких примеров таких методов — Ng-Jordan-Weiss (NJW). Это популярный алгоритм спектральной кластеризации, который особенно хорошо работает с данными в виде графов.
Основная идея NJW заключается в замене задачи кластеризации исходных данных, где могут быть сложные границы между кластерами, на задачу кластеризации в спектральном пространстве, где эти границы становятся проще. Давайте рассмотрим, как работает этот алгоритм:
- Считаем нормализованный симметричный лапласиан в виде:
- Решаем задачу поиска собственных векторов:
- Берем только из них, соответствующие самым большим собственным значениям.
- Собираем векторы в матрицу:
- Нормируем строки:
Результатом этой нормировки становится то, что каждый объект теперь представлен как точка на -мерной единичной сфере.
- К строкам применяем алгоритм .
Классический пример, когда спектральная кластеризация работает гораздо лучше обычного , — это датасет с лунами :
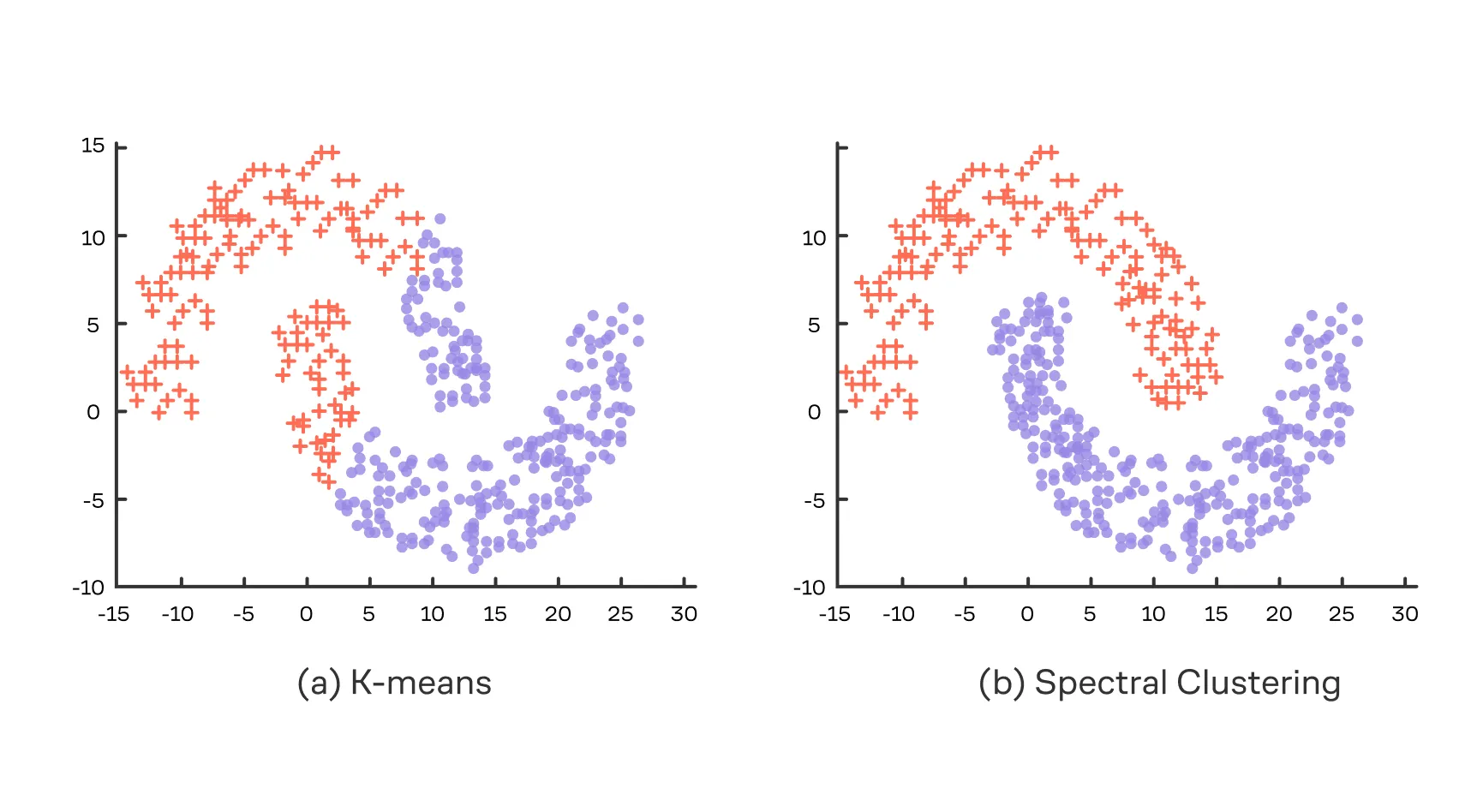
Данный алгоритм достаточно тесно связан с задачей минимального нормализованного разреза (англ. Normalized Cut), в которой мы хотим разбить граф на части так, чтобы между кластерами связей было минимум, но при этом полученные части были большими в смысле суммы степеней. Для двух частей это можно записать вот так:
Разобранный нами алгоритм буквально выдаёт приближенное решение этой задачи.
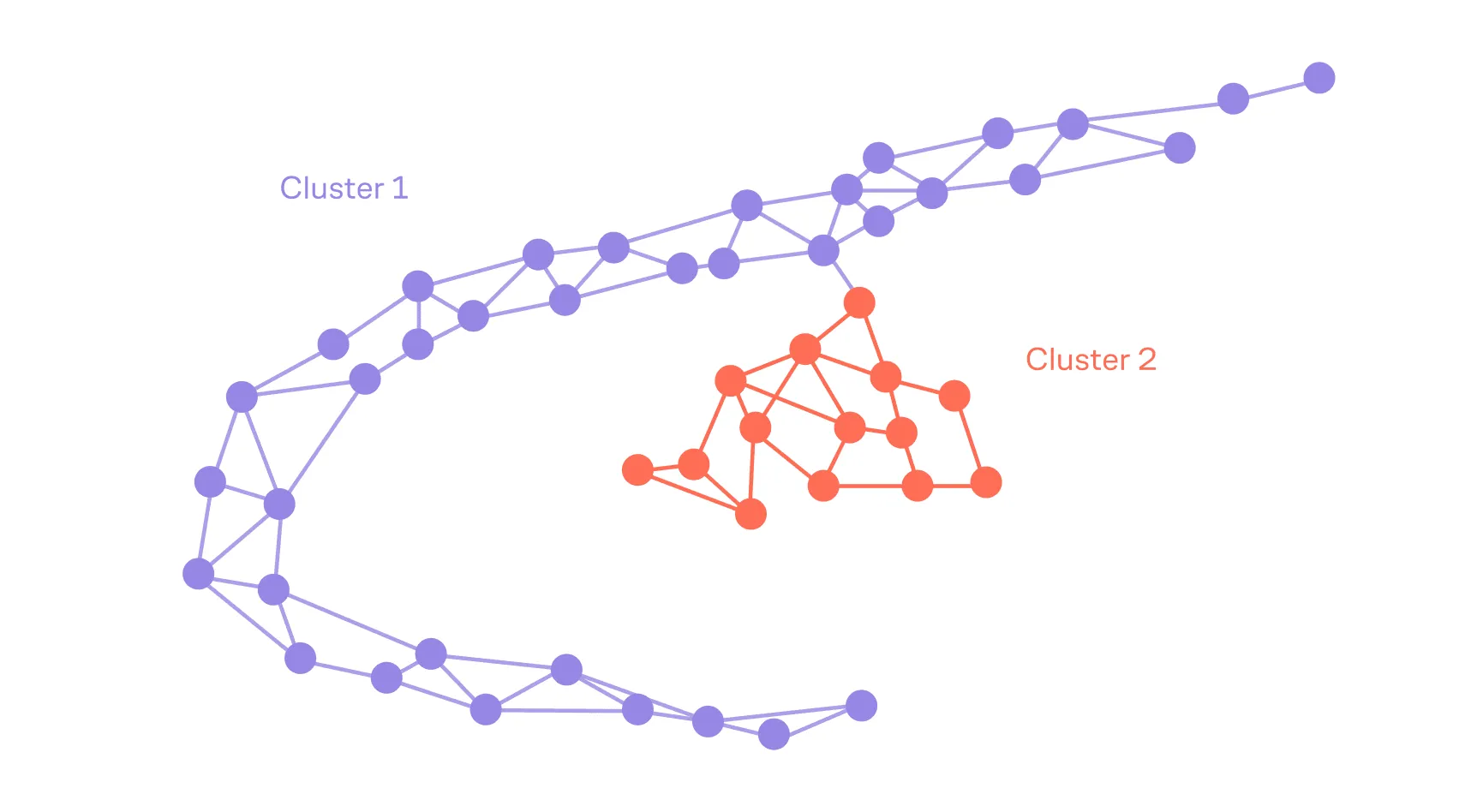
Спектральная кластеризация, запущенная на, например, модифицированном графе социальной сети (вершины — люди, а рёбра обладают весом, пропорциональным частоте общения), выделит сообщества друзей/коллег/одноклассников.
Кластеризация — не единственный способ снять структуру графа. Даже когда мы не хотим разбивать вершины на группы, нам часто нужны осмысленные признаки узлов и рёбер, чтобы подать их в табличные ML-модели. Ниже соберём такой набор.
Признаки из графа для DS-задач
Выше мы разобрались с устройством графов и с некоторыми особенностями работы на них при помощи лапласиана и ядер. Сейчас соберём и чуть расширим набор признаков, которые мы можем извлечь из графа и подать в классические табличные ML-модели (логистическая регрессия, деревья/бустинг — например, CatBoost, XGBoost).
Такой подход нужен потому, что эти модели принимают на вход привычные векторные признаки, а не сырые графовые структуры.
Степень (англ. degree). Количество рёбер вершины. В случае ориентированного графа делят на входящую и исходящую степени.
Коэффициент кластеризации (англ. clustering coefficient). Показывает, насколько плотно связаны между собой соседи вершины. Записывается для вершины c соседями так:
В случае ненаправленного графа стоит считать количество рёбер с коэффициентом два (один раз за входящее и один раз за исходящее ребро), поскольку всего рёбер у таких соседей может быть не как в ориентированном графе, а .
Центральность (англ. centrality). Оценивает важность узла в графе и бывает нескольких видов:
- Центральность по степени (degree centrality): , но иногда нормировку опускают.
- Количество кратчайших путей, которые проходит узел (англ. betweenness): , тут — число кратчайших путей из в , а — число таких путей через .
- Средняя близость к остальным (англ. closeness):
Спектральные признаки. Уже полюбившиеся нам собственные вектора (или их функции) как компактное спектральное описание локальной/глобальной структуры. Обычно берут несколько первых в качестве эмбеддингов.
Эмбеддинги. Полученные методами из прошлых частей нашего рассказа.
Дальше для каждой вершины можно собрать, например, такую конструкцию:
Проделав действия выше для каждой вершины, мы получим таблицу. И уже её можно передать вашему любимому ML-алгоритму для таблиц.
Приведём несколько задач, в которых такие признаки будут полезны:
- Антифрод. Поиск мошеннических транзакций или мошеннических аккаунтов: подозрительные операции и пользователи часто имеют аномальные степени и низкий коэффициент кластеризации.
- Соцсети. Поиск лидеров групп или сообществ с помощью центральности.
- Кредитный скоринг в развивающихся странах. Работает по принципу «скажи, кто твой друг, а я скажу, кто ты»: если у человека много связей с вершинами-банкротами, то вполне вероятно, что такой человек более склонен к банкротству.
Navigable Small World и приближённый поиск
Познакомимся теперь с алгоритмом Navigable Small World (NSW) и его иерархической модификацией (HNSW).
NSW / HNSW — это структуры графа, в которых точки (векторы) соединяются рёбрами с несколькими ближайшими «друзьями», так что «жадный» поиск по графу (следуя к ближайшему соседу) быстро приводит к узлам, близким к запросу.
Про NSW можно думать так: «каждый человек хранит контакты ближайших знакомых». Чтобы найти человека с нужными интересами, ты начинаешь с известного «центра» и шаг за шагом переходишь к знакомым, которые кажутся ближе к цели, и очень быстро подходишь к «кластеру» нужного типа.
Зачем это надо? Если у вас достаточно большой граф, то честный поиск затянется и будет работать очень долго. Но мы с вами знаем, что предоставить быстрый примерный ответ лучше, чем отправить пользователя ждать. Можно ли как-то быстро получить быстрый примерный ответ и потенциально доработать его?
Граф строится итеративно: каждая новая вершина добавляется в уже построенный граф и соединяется с вершинами, ближайшими к ней по локальному поиску, а не по всему множеству.
Алгоритм вставки вершины :
- Выполняется локальный эвристический поиск ближайших к вершин.
- Выбираются ближайших среди найденных.
- Добавляются рёбра между и этими вершинами.
Это создаёт граф, обладающий свойствами малого мира с короткими путями между произвольными вершинами и высокой кластеризацией.
Алгоритм поиска:
- Начинаем с произвольной вершины .
- Если находим соседа — такого, что: , переходим в .
- Иначе возвращаем как результат.
Это локальный жадный поиск (англ. greedy search), останавливающийся в локальном минимуме.
В чем же идея иерархический модификации?
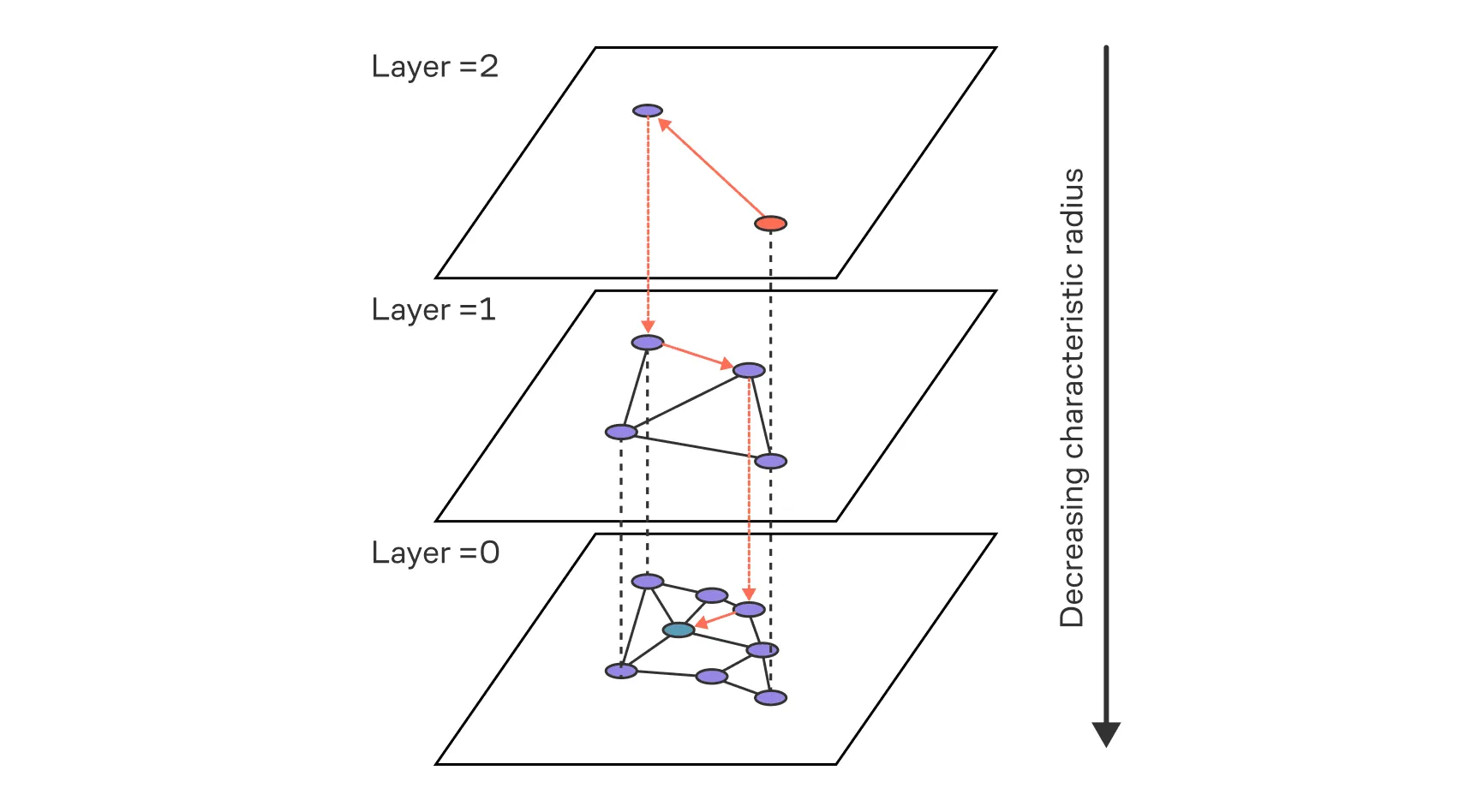
Добавляется иерархия уровней — граф становится многоуровневым. Верхние уровни разрежены, нижние — плотные. Навигация начинается с самого верхнего иерархического уровня и постепенно переходит вниз, улучшая приближение.
Представьте, будто у вас есть несколько вариантов транспорта: нижний уровень будет идти пешком, повыше — автобусом или трамваем, уровень ещё выше — поездом, а самый высокий — самолётом. Пешком вы можете достичь любой точки, но медленно, а самолет позволяет быстро перемещаться, но только между аэропортами.
Алгоритм вставки точки такой:
- Случайно назначаем точке максимальный уровень (геометрическое распределение).
- Стартуем с текущего верхнего уровня и жадно спускаемся до , каждый раз переходя к ближайшим к .
- На каждом уровне выполняем локальный поиск кандидатов и соединяем с «разнообразными» ближайшими узлами (используется эвристика отбора соседей).
- Обновляем верхний уровень при необходимости.
Алгоритм поиска такой:
- Пусть запрос . Начинаем с вершины на верхнем уровне и выполняем жадный поиск по уровню.
- Переходим на уровень ниже, стартуя с лучшего найденного узла.
- Повторяем до нулевого уровня.
- На уровне 0 выполняется расширенный поиск с буфером из нескольких вершин (priority queue), чтобы избежать локального минимума.
В этом параграфе мы изучили, как рассматривать граф как сигнальное пространство: определять его спектр и частоты, моделировать распространение информации через диффузию и случайные блуждания, выделять значимые паттерны с помощью фильтров, а также представлять вершины и целые графы в виде эмбеддингов. Мы познакомились с ядрами и методами кластеризации, которые позволяют выявлять скрытые структуры и сходства, даже не прибегая к нейросетям.
Эти подходы образуют математический фундамент графовых нейронных сетей (GNN). Спектральный анализ задаёт язык сверток на графах, диффузионные процессы описывают передачу сигналов между вершинами, а эмбеддинги обеспечивают компактное кодирование структуры.
А сейчас — пройдите квиз, чтобы закрепить знания, и переходите к заключительному параграфу главы: там мы коротко подведём итоги.



