В предыдущем параграфе мы научились вычислять непростые производные и градиенты функций и даже поняли, как работает бэкпроп (метод обратного распространения ошибки) в нейронных сетях: мы подготовили базу для обучения моделей.
В этом параграфе мы пойдем дальше и поговорим непосредственно о методах, при помощи которых модели обучаются, — это градиентные методы. Разберёмся, зачем мы считали производные функции потерь по весам в нейронной сети и зачем они вообще нам нужны.
Наша основная цель в машинном обучении — получить самую хорошую прогнозную модель, то есть модель, которая делает предсказания с наименьшей ошибкой. Для этого мы обычно минимизируем функцию потерь, то есть решаем задачу:
Здесь — функция потерь (ошибка модели), — веса модели. Значения функции потерь считаем на обучающей выборке . То есть нам надо найти такие веса, при которых значение функции потерь минимально. А как решить эту задачу?
Оказывается, чтобы найти минимумы дифференцируемых функций, можно воспользоваться свойством градиента, которое мы уже знаем: градиент показывает направление наискорейшего роста функции. На этом свойстве основан метод градиентного спуска, который используется повсеместно в машинном обучении для нахождения минимумов различных функций потерь — разберём его подробно.
Градиентный спуск
Далеко не всегда мы можем решить задачу нахождения минимума функции потерь аналитически. На самом деле в большинстве случаев аналитического решения как раз нет. А если и есть, то может быть нестабильным или вычисляться долго.
Отличная альтернатива точному (аналитическому) решению — градиентный спуск. Это итеративный подход, с помощью которого мы можем за несколько итераций с очень хорошей точностью найти решение.
Суть градиентного спуска (англ. — Gradient Descent, или сокращённо GD) состоит в следующем:
Шаг 1. Мы начинаем поиск оптимального вектора весов обычно из некоторой случайной точки.
Шаг 2. Далее действуем итеративно: находясь на -м шаге в некоторой точке , мы вычисляем градиент , который указывает направление наискорейшего роста функции. Чтобы уменьшить значение функции, мы двигаемся в противоположную сторону — по направлению антиградиента. Повторяя этот процесс шаг за шагом, мы постепенно приближаемся к минимуму.
Формула одного шага градиентного спуска:
Шаг 3. В какой-то момент, когда на очередной итерации метода градиент будет около , мы останавливаем метод и получаем итоговый вектор весов — это и есть наш искомый вектор весов, ведь мы (с большой вероятностью) на всём пути шли и пришли в минимум функции потерь. А в минимуме, как мы знаем, градиент равен .
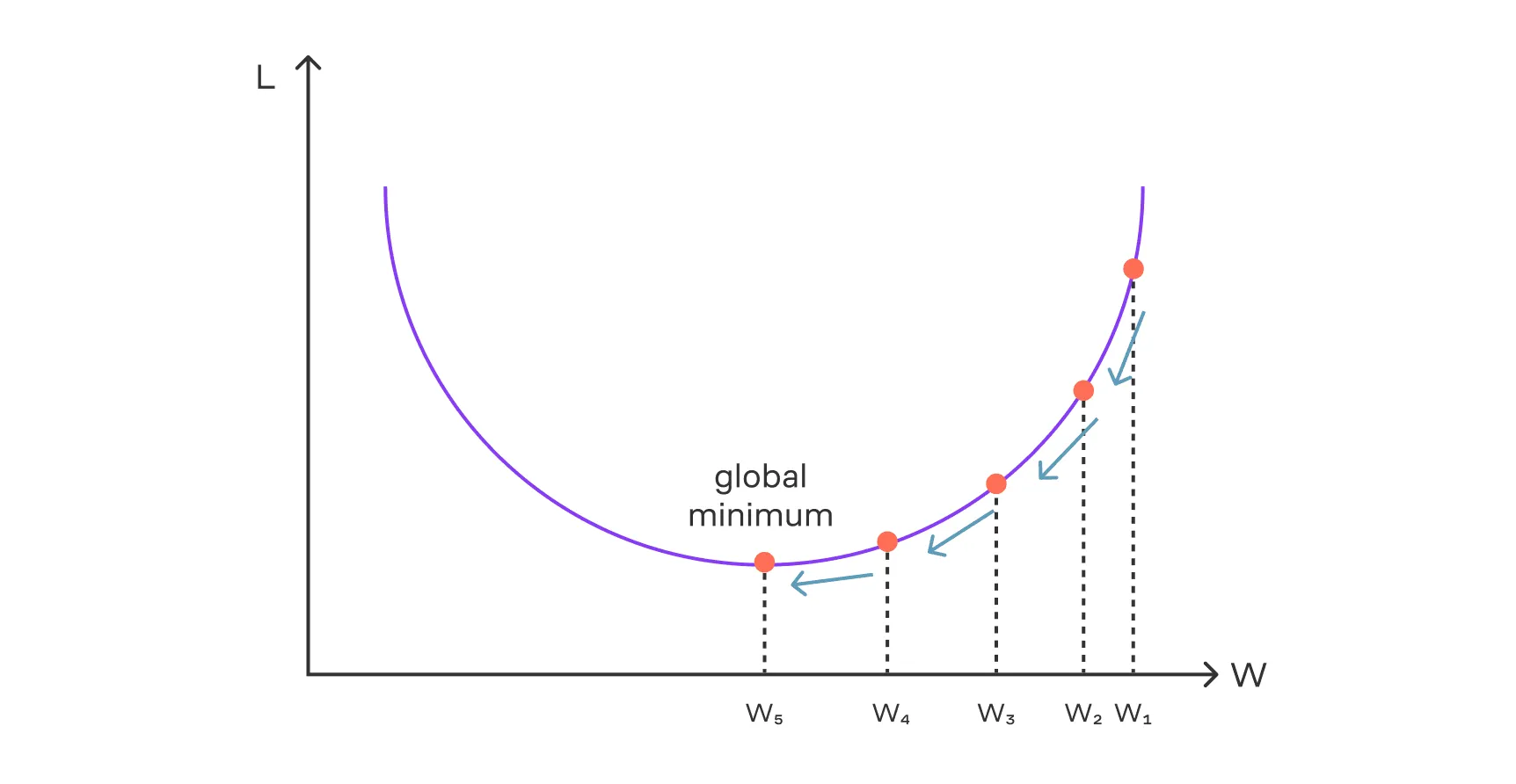
Важный параметр метода — это скорость сдвига вдоль антиградиента, то есть размер шагов по направлению к минимуму. Этот параметр называется скоростью обучения (англ. — learning rate).
В формуле выше мы обозначаем его как . Если шаг слишком большой, модель может перескочить через минимум и начать блуждать. Если же шаг слишком маленький, обучение будет проходить слишком медленно и затянется.
Стохастический градиентный спуск
Сам по себе градиентный спуск — простой метод, но для достижения минимума обычно требуются тысячи или десятки тысяч итераций. При этом на каждой итерации мы вычисляем градиент функции потерь по всей обучающей выборке:
где — объекты обучающей выборки, а — их количество.
При этом каждый градиент — это набор из частных производных по всем весам модели (пусть в модели весов).
То есть на каждом шаге градиентного спуска мы для каждого объекта вычисляем производные по всем весам: другими словами, делаем операций. Это очень много — с учётом того, что в современных глубоких нейронных сетях триллионы параметров (весов) и обучаются они на миллионах обучающих объектов.
У нас нет возможности ждать годами, пока обучится одна модель. Поэтому существуют модификации классического градиентного спуска, которые без потери точности работают значительно быстрее.
Стохастический градиентный спуск
Первая модификация называется стохастическим градиентным спуском (англ. — Stochastic Gradient Descent, сокращённо SGD). Суть метода в следующем: давайте на каждой итерации градиентного спуска вычислять градиент по одному случайно взятому объекту выборки. Получится гораздо быстрее!
Благодаря такому подходу на каждой итерации метода мы делаем всего вычислений, что сильно ускоряет процесс. Однако поскольку на каждой итерации мы выбираем лишь один объект, метод становится шумным, и для сходимости требуется больше итераций.
Мини-батч-градиентный спуск
Лучшим решением будет найти золотую середину между классическим градиентным спуском, где мы считаем градиенты по всей выборке (батч-подход), и стохастическим градиентным спуском — этот вариант реализации метода называется мини-батч-градиентный спуск (сокращённо — mini-batch GD).
В этом методе мы фиксируем размер группы объектов (это и есть мини-батч), а затем на каждой итерации вычисляем по ней градиент. В мини-батче может быть 32, 64 или любое другое количество объектов.
Здесь — сумма по объектам из батча .
Такой подход даёт нам вычислений на каждой итерации метода, где — небольшая константа. Поэтому по сложности он сопоставим со стохастическим градиентным спуском, а по точности гораздо более устойчив и сходится быстрее.
Для наглядности опишем все три метода в виде таблички:
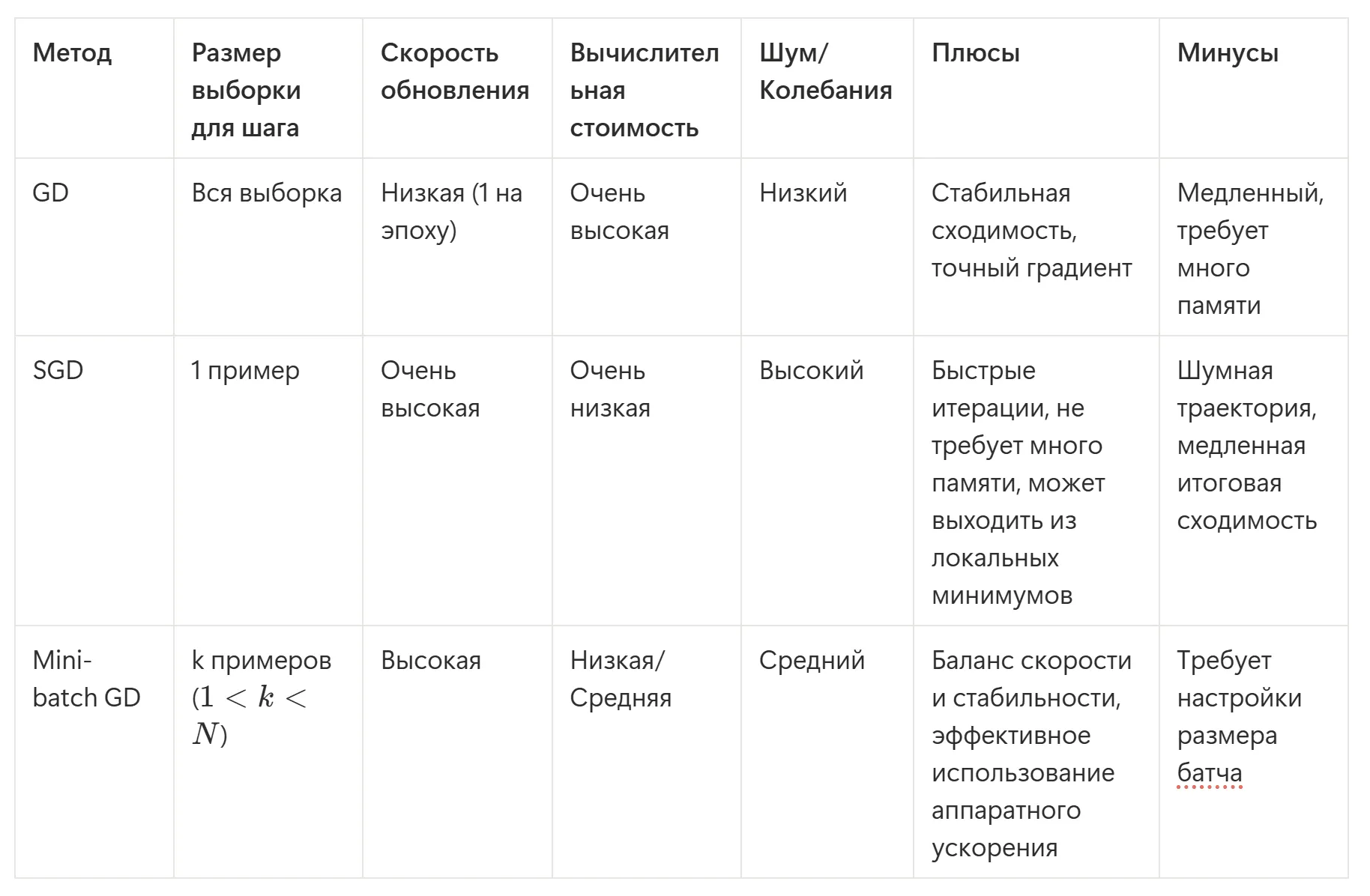
Сейчас для обучения нейронных сетей де-факто используют только мини-батч-подход. Но так как он тоже стохастический (содержит случайность), на практике его часто называют стохастическим градиентным спуском. Имейте в виду и не перепутайте!
Казалось, тут можно бы и закончить с градиентными методами, так как основную задачу — поиск минимума функции потерь — мы вроде бы решили. Но не совсем.
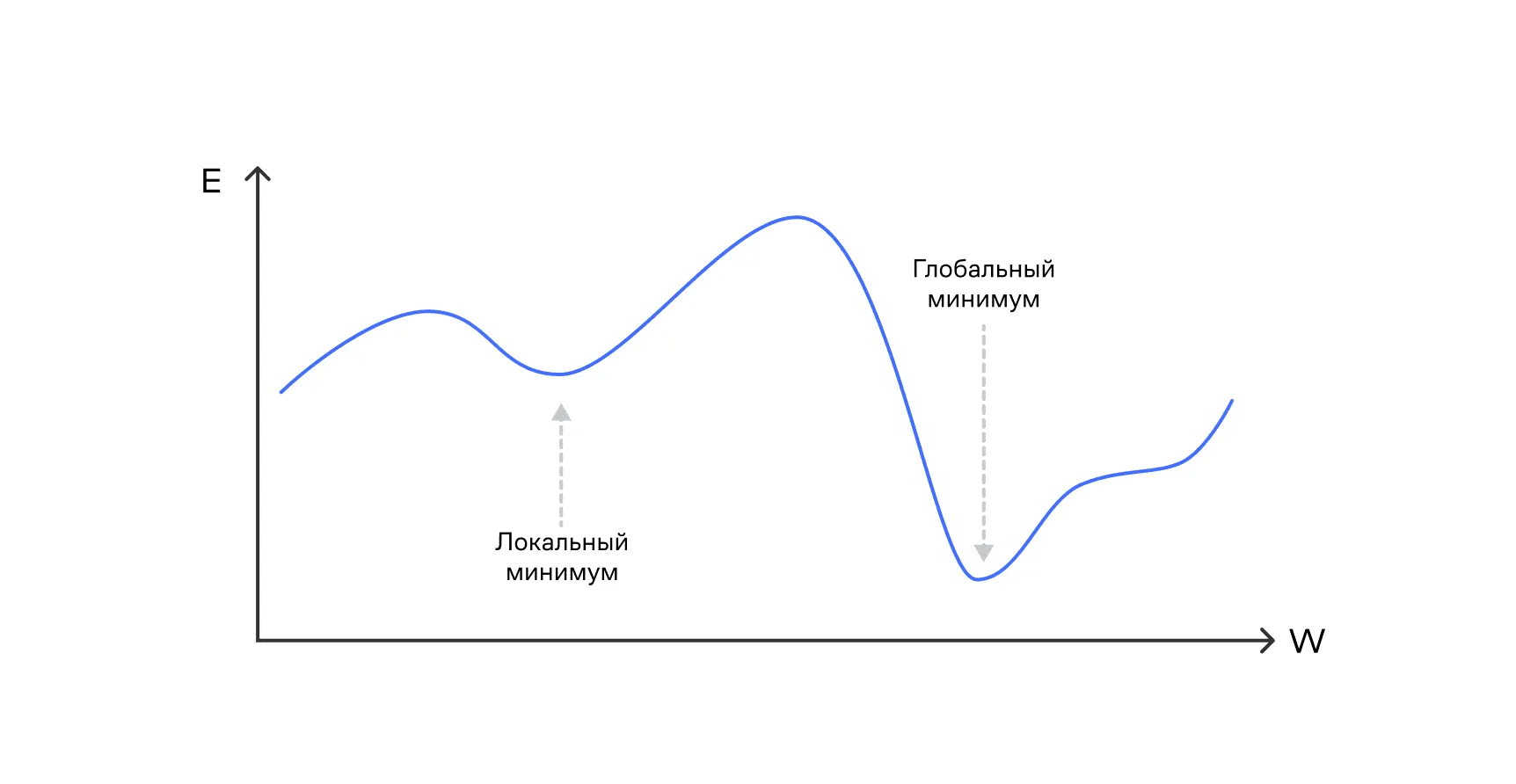
К сожалению, применение SGD не гарантирует нам попадания в минимум функции потерь. Что может произойти в плохом сценарии:
- Мы можем попасть в локальный (но не глобальный) минимум функции потерь — там градиент также равен нулю, и метод остановится.
- Мы можем вообще не дойти до минимума из-за сложности и разнородности ландшафта функции потерь.
Чтобы решить эти проблемы и научиться находить правильный минимум даже у сложных функций потерь, нам придётся немного погрузиться в теорию оптимизации, поговорить про вторые частные производные и затронуть вопросы условной оптимизации.
К слову, условная оптимизация нам пригодится не только для поиска минимумов функций потерь, но и для решения ряда других задач анализа данных — поэтому давайте ненадолго прервёмся и поговорим про оптимизацию.
Экстремумы и оптимизация
В предыдущих параграфах мы часто использовали понятие градиента и строили на этом рассуждения. В частности, градиентный спуск основан на свойствах градиента. Но градиент — многомерное обобщение производной — даёт нам только необходимую информацию о том, попали ли мы в локальный минимум.
К сожалению, значение градиента не отвечает однозначно на вопрос, находимся ли мы в локальном минимуме, локальном максимуме функции или же в точке перегиба — для ответа на этот вопрос нам нужно глубже изучить функцию, применяя вторые частные производные.
Ниже давайте математически точно обозначим нужные нам понятия.
Критические точки
Для функции нескольких переменных точки, в которых градиент обращается в ноль, называются критическими или стационарными:
В этих точках может находиться локальный минимум или максимум функции — или же там может быть точка перегиба. Интуитивно это легко понять. Градиент всегда указывает в направлении наискорейшего роста функции.
Если градиент равен нулю, это означает, что мы находимся на ровном месте. Продолжая «рельефную» метафору — на вершине холма, на дне впадины или на перевале (седловой точке), где нет очевидного направления для мгновенного подъёма или спуска. Именно в таких точках и могут находиться искомые нами экстремумы.
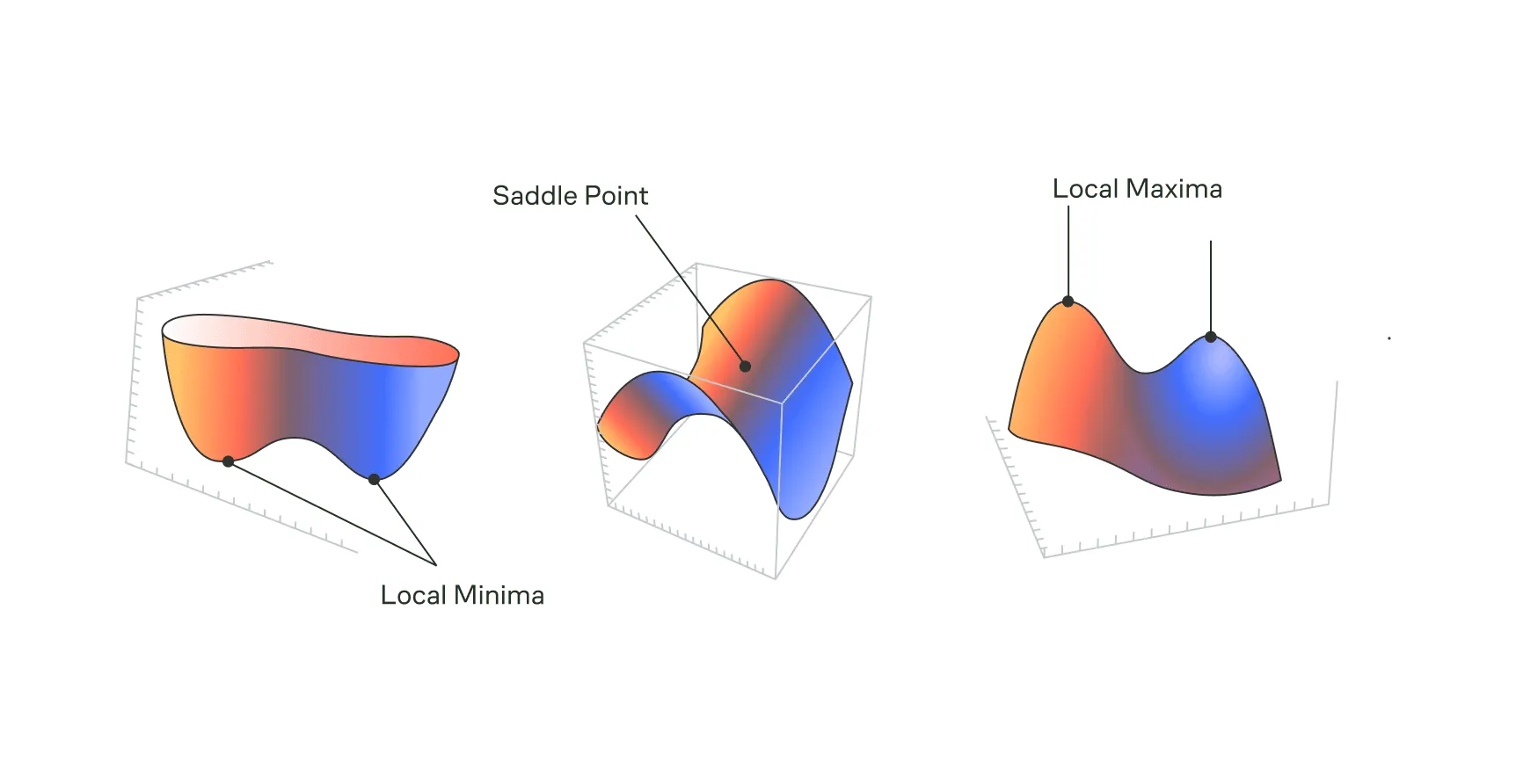
Когда в критической точке градиент функции равен нулю, возникает вопрос: что это за точка — минимум (дно впадины), максимум (вершина) или, может быть, седловая точка (точка перегиба)?
Чтобы ответить на этот вопрос, используют аналог второй производной для функций многих переменных — матрицу Гессе, или гессиан. Это квадратная матрица , в которую входят все возможные вторые частные производные функции.
Пусть функция задана на векторе . Тогда элемент матрицы Гессе на пересечении -й строки и -го столбца вычисляется по формуле:
Матрица Гессе описывает локальную кривизну функции. Гессиан позволяет заглянуть вглубь поверхности функции и оценить её форму в окрестности критической точки, используя информацию не только о наклоне, но и о его изменении.
Градиент и гессиан позволяют сформулировать критерии, которые дают нам точное понимание о точке, в которую мы попали, например, используя метод градиентного спуска.
Критерии второго порядка
Чтобы определить тип критической точки , в которой градиент , необходимо вычислить и проанализировать матрицу Гессе в этой точке. Характер критической точки зависит от матрицы Гессе:
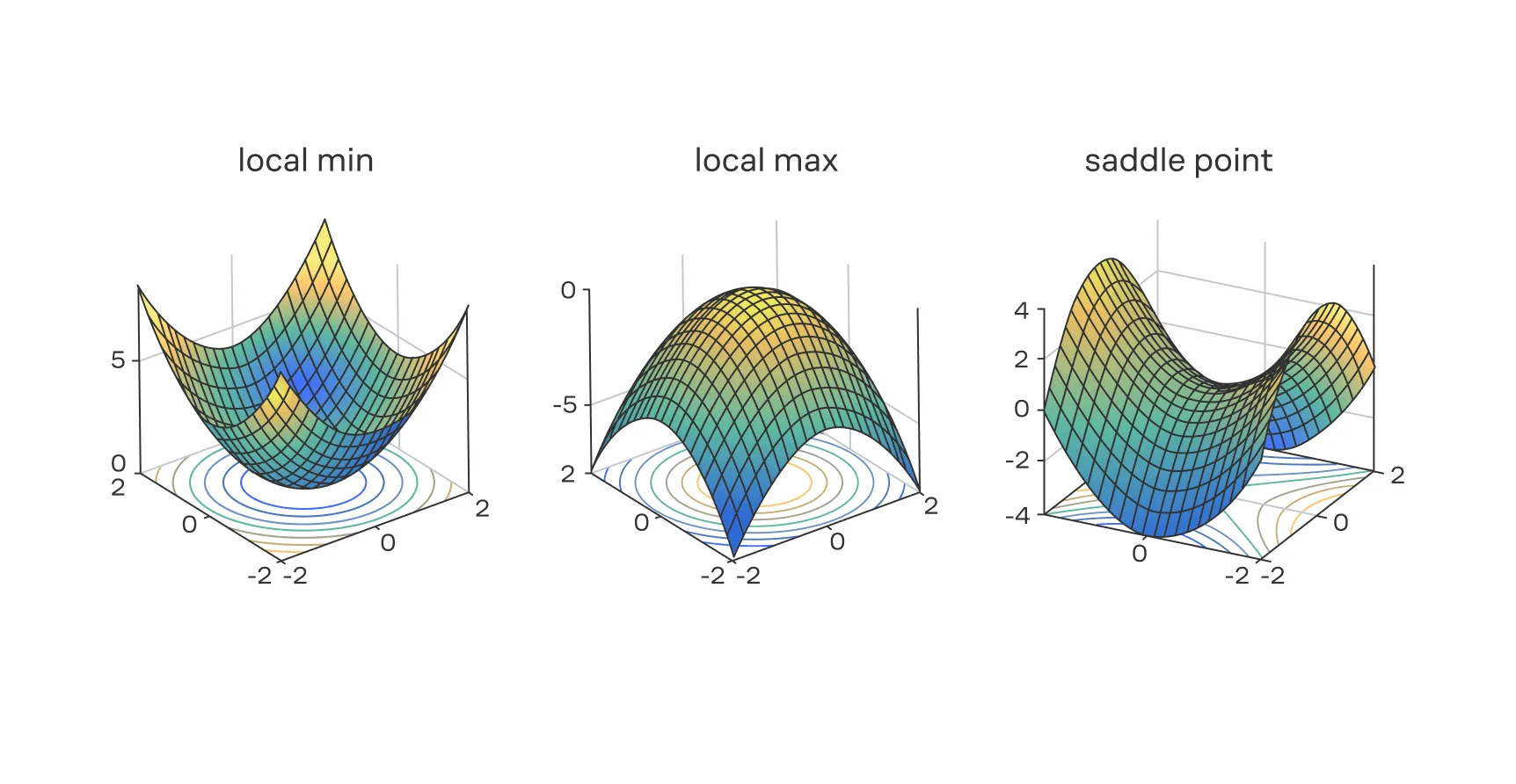
- Если матрица положительно определена (все собственные значения строго положительные), то — это
локальный минимум. Геометрически это означает, что поверхность функции в этой точке изогнута вверх во всех направлениях, как дно чаши. - Если матрица отрицательно определена (все собственные значения строго отрицательные), то точка является
локальным максимумом. Поверхность при этом изогнута вниз, как купол. - Если матрица неопределённая (имеются как положительные, так и отрицательные собственные значения), то точка — это
седловая точка. Вдоль одних направлений функция возрастает, вдоль других — убывает. Форма поверхности напоминает седло. - Если матрица
вырождена(одно или несколько собственных значений равны нулю), то анализ с помощью второй производной не даёт однозначного ответа. В таком случае необходимо прибегнуть к дополнительным методам исследования.
Теперь мы точно знаем, как определить тип критической точки, и это здорово. Но рассматривать гессиан просто как инструмент для теста — значит упускать его истинную мощь.
Глубинное понимание заключается в том, чтобы видеть в нём полную карту локальной геометрии поверхности потерь. Градиент указывает на самое крутое направление, но гессиан описывает саму форму долины или холма, на котором мы находимся. Его собственные векторы указывают на главные оси кривизны, а соответствующие им собственные значения количественно определяют, насколько эта кривизна резкая или плавная в этих направлениях.
Например, большое положительное собственное значение гессиана означает резкий изгиб вверх в направлении соответствующего собственного вектора. Малое положительное собственное значение указывает на очень плоскую, пологую кривую. Это имеет прямое отношение к сложностям оптимизации в машинном обучении.
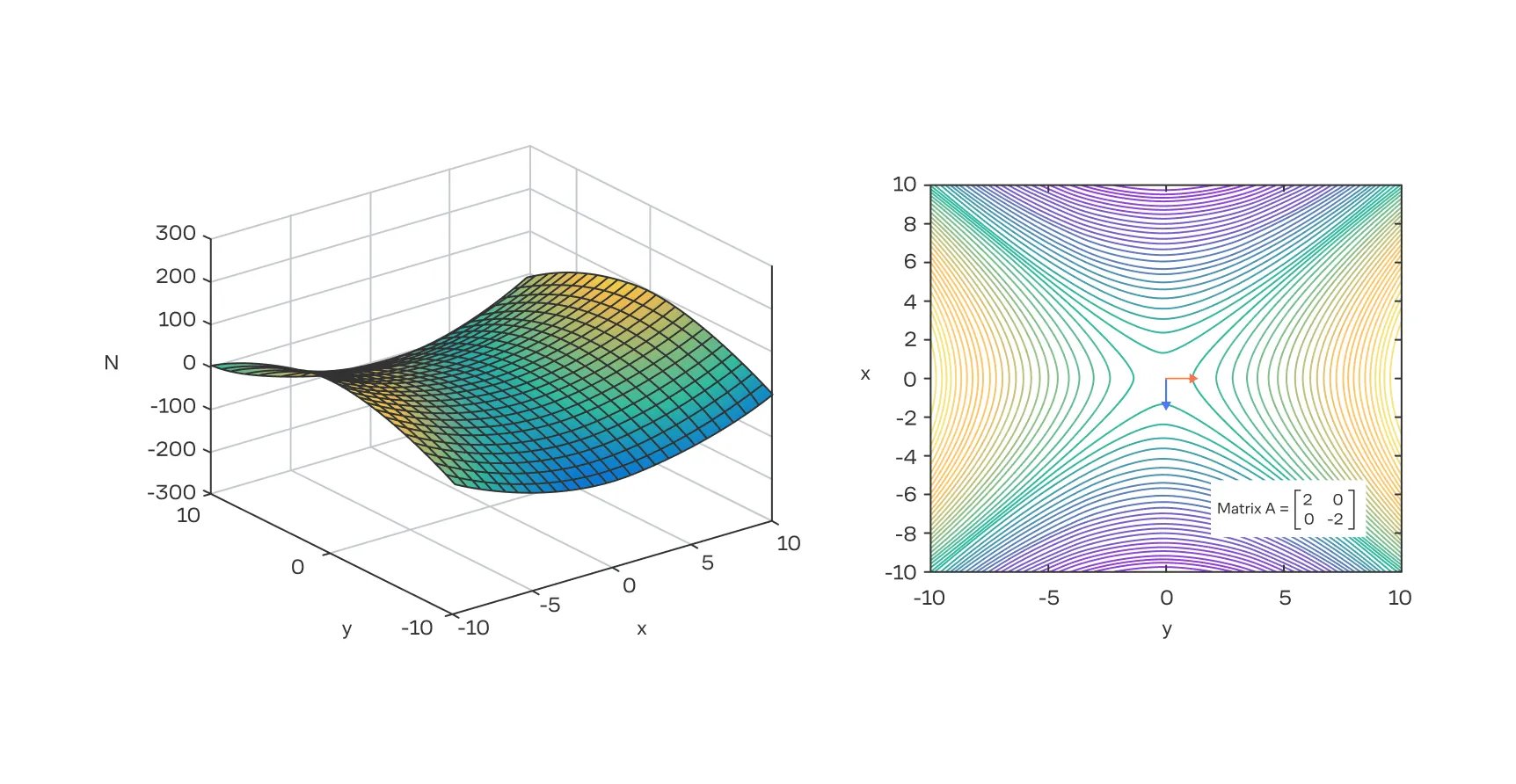
Ландшафт функций потерь в машинном обучении
Анализ поверхности функции потерь с помощью градиента и гессиана — это не просто теоретическое упражнение. Он помогает понять, насколько сложна задача оптимизации для конкретной модели и почему некоторые алгоритмы работают лучше других.
Например, в глубоком обучении, где ландшафты потерь невероятно сложны, седловые точки встречаются гораздо чаще, чем плохие локальные минимумы. Понимание геометрии, описываемой гессианом, объясняет, почему простые методы оптимизации могут застревать на таких плато и медленно сходиться. Это знание мотивирует разрабатывать и использовать более сложные алгоритмы, способные эффективно ориентироваться в таких сложных пространствах.
Далее гессиан пригодится нам в методах второго порядка (таких как метод Ньютона) и адаптивных градиентных методах, которые являются улучшениями классического градиентного спуска — как раз о них и о других модификациях градиентного спуска мы и будем говорить дальше.
Модификации градиентного спуска
Подробно эта тема разбирается в хендбуке по машинному обучению, но здесь расскажем вам, зачем придуманы различные модификации метода и какие проблемы они решают.
У классического градиентного спуска есть две большие проблемы:
Проблема 1: застревание в локальных минимумах функции, ведь когда мы попадаем близко к точке, где градиент равен нулю (а это может быть не глобальный минимум) — веса перестают обновляться.
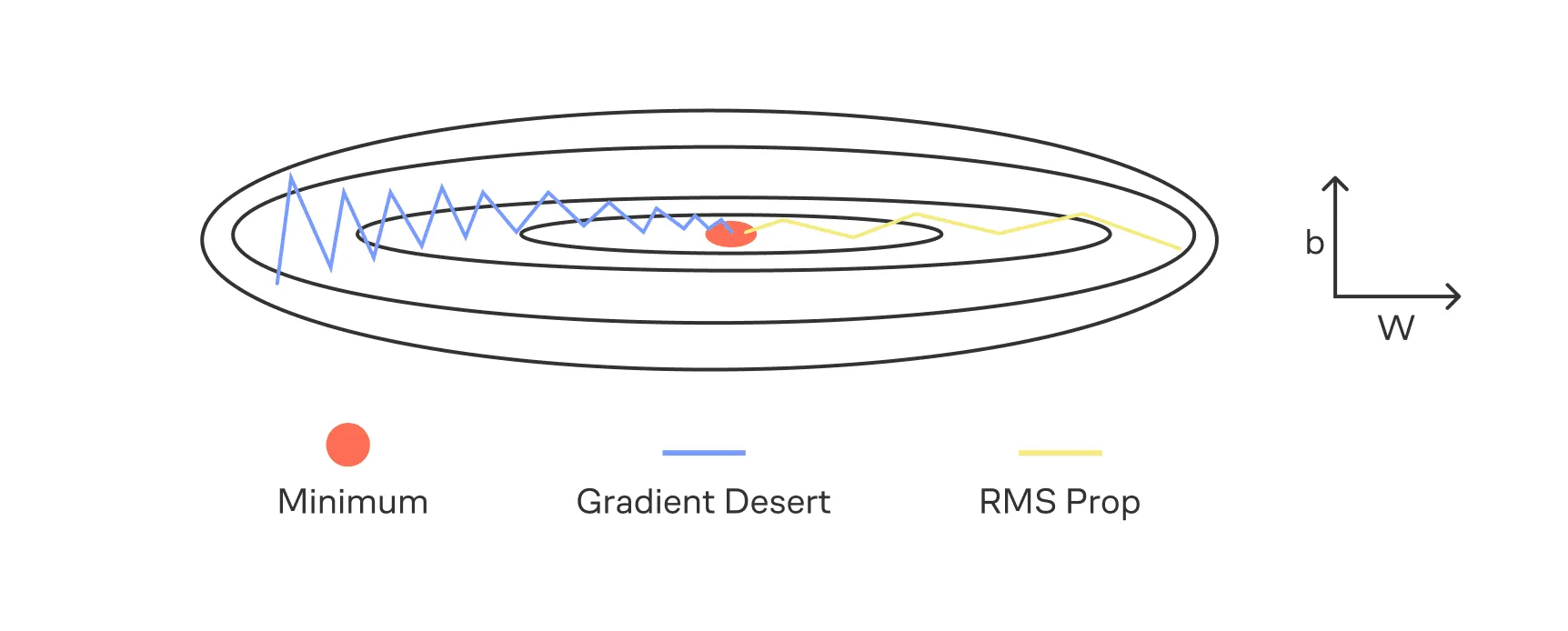
Проблема 2: по разным координатам поверхность функции потерь может сильно различаться. Представьте себе вазу: по одной координате спуск очень пологий, а по другой — очень крутой. И для градиентного спуска с фиксированным градиентным шагом это большая проблема. Если шаг слишком большой, то градиентный спуск разойдётся по «крутой» координате, а при меньших шагах нам может не хватить скорости дойти до минимума по «пологой» координате.

Для решения этих проблем существуют модификации метода градиентного спуска. Самые известные из них — это RMSprop и Adam.
RMSprop
Основная идея метода RMSprop (англ. — Root Mean Square Propagation) — адаптировать скорость обучения индивидуально для каждого параметра. Алгоритм делит шаг обучения на корень из экспоненциально сглаженного среднего квадрата градиентов по этому параметру.
Интуитивно это можно понимать так: если скорость сдвига по некоторой координате (весу) большая, то есть градиент большой, то мы должны замедляться при движении к минимуму, чтобы его точнее искать. В случае малой скорости движения мы, наоборот, хотели бы двигаться быстрее.
Такой подход позволяет справляться со второй проблемой, указанной выше, — с сильными различиями формы поверхности функции потерь по разным координатам.
Adam
Adam (англ. — Adaptive Moment Estimation) — это один из самых популярных и надёжных оптимизаторов на сегодня. Он сочетает в себе две ключевые идеи и решает обе проблемы классического градиентного спуска.
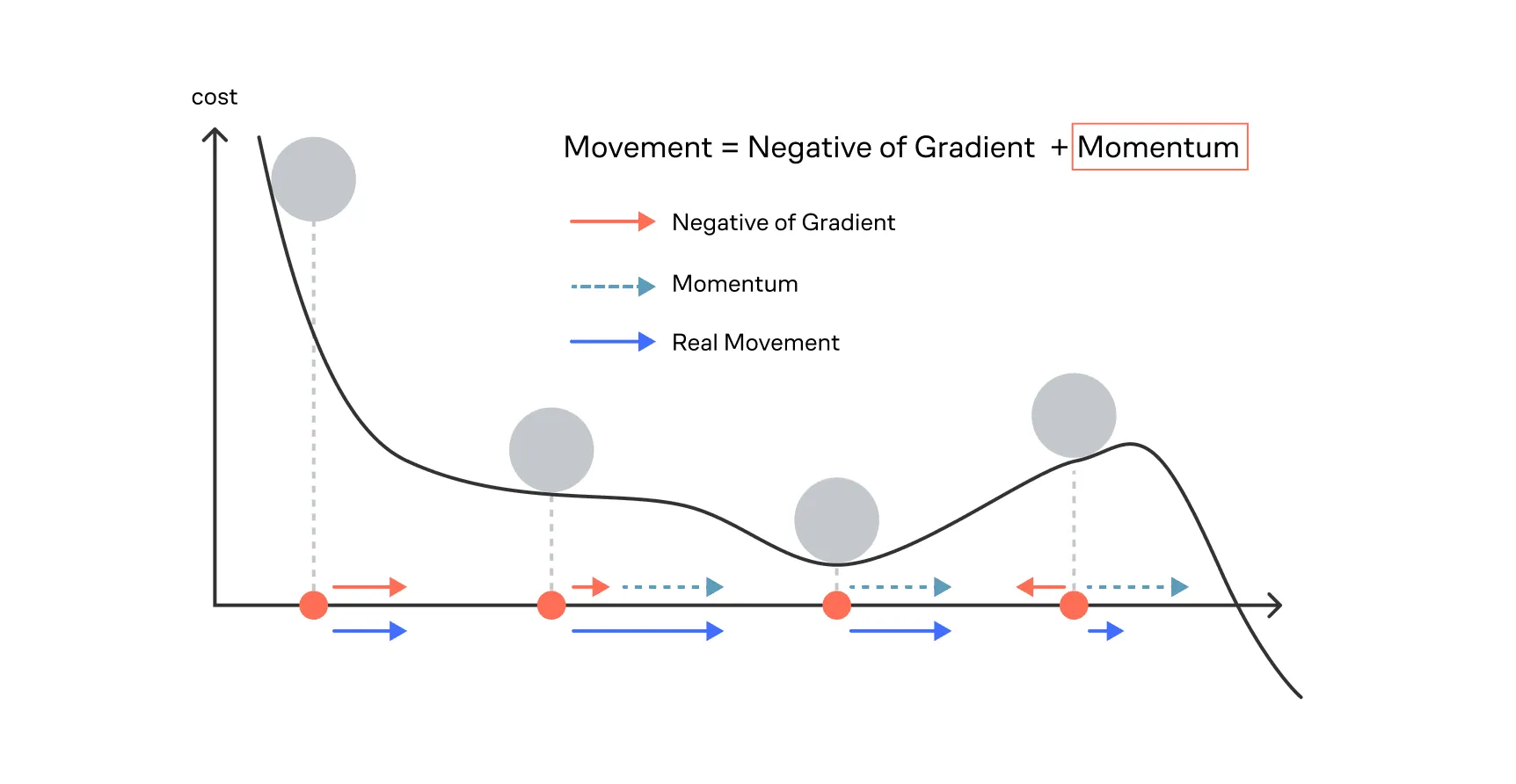
Идея 1: добавление инерции (Momentum)
Алгоритм хранит экспоненциально сглаженное среднее самих градиентов — это первый момент. Простыми словами, это означает, что мы добавляем в метод память о движении, то есть, попадая в локальный минимум, метод не остановится (как в классическом градиентном спуске, так как там градиент равен нулю), а как мячик, попавший в ямку, сможет из неё выпрыгнуть при большой накопленной скорости и покатиться в другой локальный минимум.
Идея 2: использование адаптивного шага (как в RMSprop)
Так же, как RMSprop, Adam отслеживает второй момент — сглаженное среднее квадратов градиентов. Это позволяет корректировать шаг обучения для каждого параметра в зависимости от его поведения.
Иными словами, Adam — это RMSprop с добавлением инерции. Благодаря такому сочетанию он становится чрезвычайно эффективным и надёжным инструментом, особенно при обучении глубоких нейронных сетей.
Cочетание инерции и адаптивного подбора градиентного шага (скорость обучения) под каждый вес позволяет Adam эффективно искать минимумы сложнейших многомерных функций потерь, что и сделало его стандартом в глубоком обучении.
Поэтому сейчас обучение глубоких нейронных сетей, как правило, осуществляется путём минимизации функций потерь с помощью метода Adam или его модификаций (например, AdamW).
Связь вторых частных производных с модификациями градиентного спуска
Когда мы используем обычный градиентный спуск, мы движемся к минимуму функции потерь, опираясь только на градиент — то есть на скорость изменения функции в каждой точке. Но градиент не даёт информации о кривизне поверхности, то есть о том, насколько быстро меняется наклон в разных направлениях.
Адаптивные методы RMSprop и Adam тоже используют градиент, но дополнительно следят за величиной самих градиентов для каждого параметра и корректируют шаг обучения в зависимости от их «разброса» или среднего квадратичного значения.
Соберём всё вместе: вторые производные функции потерь, которые составляют гессиан, показывают кривизну поверхности — то есть то, насколько быстро меняется градиент в разных направлениях. Методы RMSprop и Adam напрямую не вычисляют гессиан, но они адаптируют размер шага для каждого параметра в зависимости от величины градиентов: при больших градиентах шаг уменьшается, при маленьких — увеличивается. Благодаря такой адаптации методы приближённо учитывают кривизну функции, то есть частично используют ту же информацию, что и гессиан, делая обучение более стабильным и эффективным.
Подведём итог. В этом параграфе мы подробнее познакомились с оптимизацией, а именно поняли, что для эффективного решения задач оптимизации в машинном и глубинном обучении нам нужен не только градиент, но и дополнительная информация о ландшафте функции потерь — например, вторые частные производные, описываемые Гессианом функции потерь.
В следующих параграфах вы узнаете об оптимизациях второго порядка, то есть о методах, которые в явном виде учитывают вторые частные производные. Но мы уже сейчас на примере RMSprop и Adam видим, что учёт дополнительной информации о форме функции потерь даёт сильное улучшение в решении задач её оптимизации.



