Представьте, что вы работаете в консалтинге. К вам обратился крупный торговый центр, который хочет оптимизировать маршруты покупателей. Проблема такая: посетители распределяются неравномерно. Где-то их слишком много и возникают заторы, а где-то их совсем нет, и владельцы магазинов жалуются на нехватку клиентов.
Конечно, можно методом проб и ошибок попробовать разные варианты навигации, но это потребует много ресурсов и не факт, что решит проблему. Другой вариант — воспользоваться теорией графов.
Дело в том, что торговый центр можно отлично представить в виде графа: комнаты и коридоры будут узлами, а пути между ними — рёбрами. С такой моделью удобнее проводить вычисления и анализировать данные.
Например, мы можем смоделировать движение покупателей с помощью алгоритмов анализа графов и найти потенциальные точки перегрузок. Или предложить наиболее короткие маршруты для популярных мест из разных точек входа. Или сделать маршрут мимо наименее посещаемых магазинов.
Вариантов много — главное, что методами теории графов можно решать задачи оптимизации, находя оптимальные пути и решения для различных процессов. А наглядная визуализация делает структуру системы более понятной, облегчая восприятие и передачу информации.
В виде графа можно представить и многие другие системы. Главное, чтобы элементы системы были связаны друг с другом. Например, это могут быть:
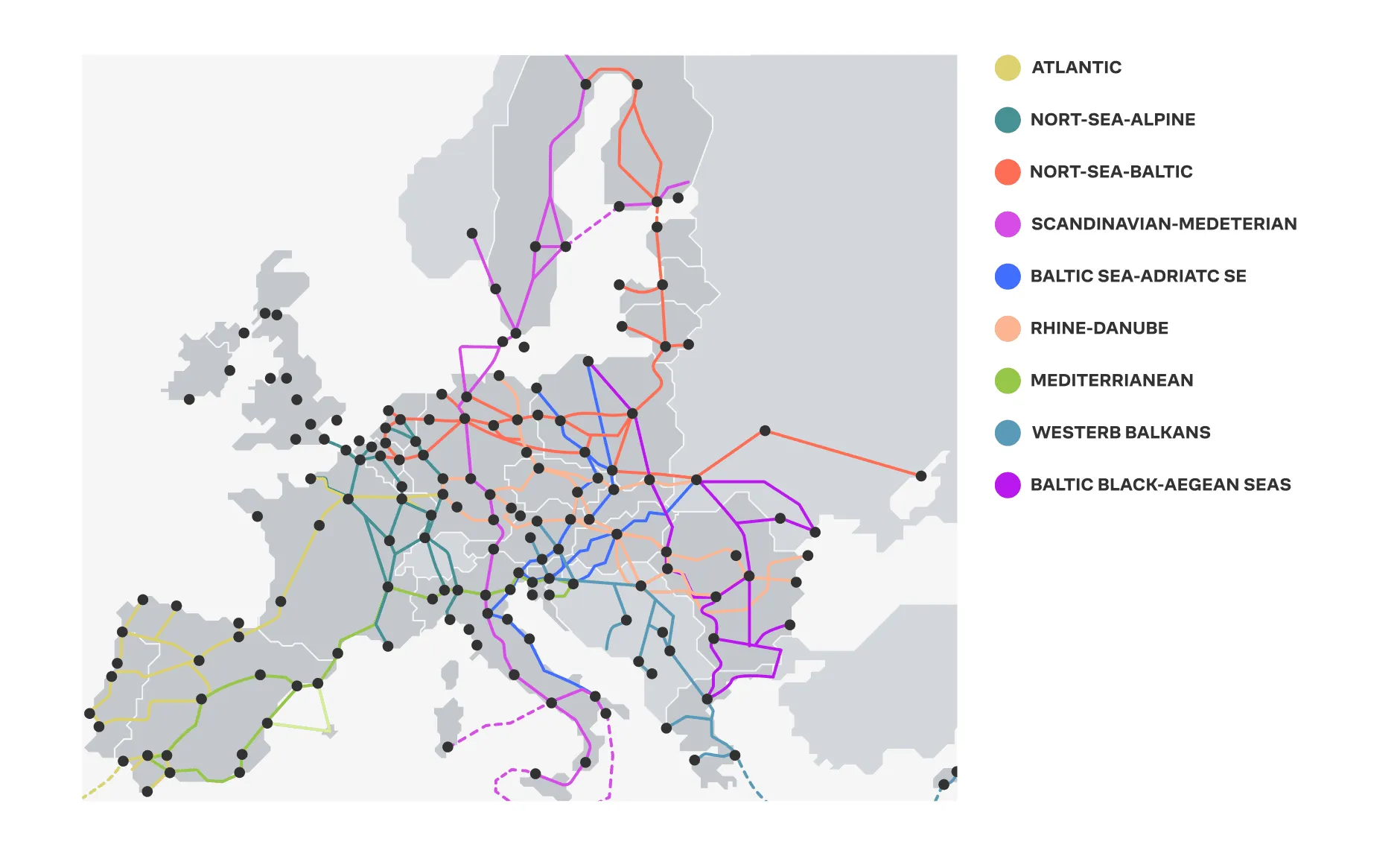
- Транспортные сети. Графы могут моделировать города как вершины и маршруты (дороги, железнодорожные линии) как рёбра.
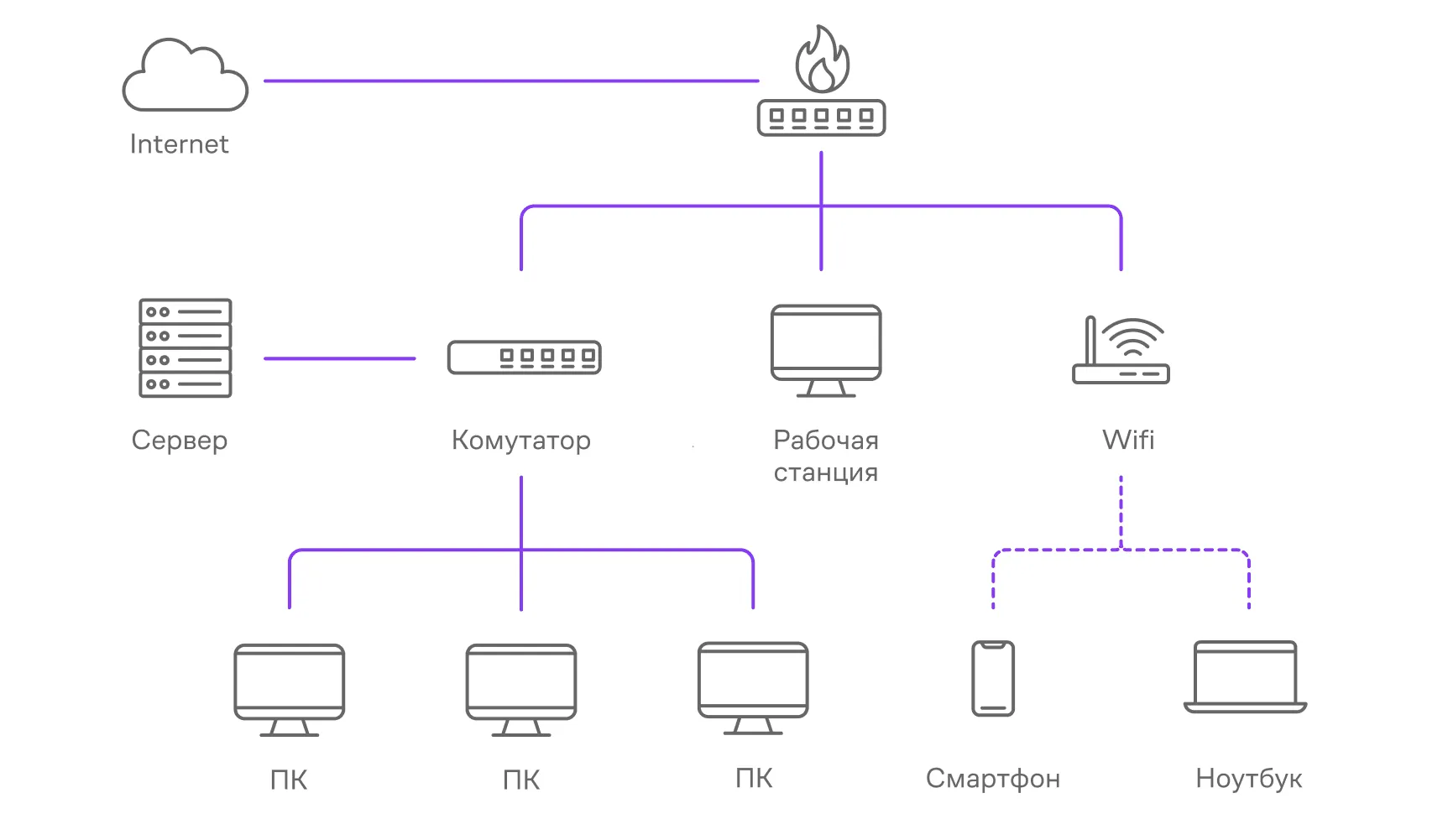
- Компьютерные сети. Компьютеры или серверы представлены как вершины, а сетевые соединения между ними — как рёбра.
- Биологические сети. Графы используются для моделирования нейронных взаимодействий, где вершины представляют собой нейроны, а рёбра — синаптические связи между ними.
А ещё графы помогают выявлять скрытые закономерности и паттерны в данных, что облегчает анализ сложных систем. Например, с помощью графов маркетологи могут сегментировать покупателей — чтобы по добавленным в корзину товарам предложить покупателю вещи, которые могут его заинтересовать, или персональную скидку.
На этом возможности графов не заканчиваются. Модели машинного и глубинного обучения можно адаптировать для работы с данными графовой структуры. Например, графовые нейронные сети позволяют моделям учитывать все переплетения связей между объектами. Это как дать модели не только перечень продуктов, но и рецепты, показывающие, как они сочетаются друг с другом. В результате предсказания становятся более точными и осмысленными.
Вот, теперь вы знаете, зачем нужны графы. Далее разберёмся, что такое граф с точки зрения математики.
Фундаментальные понятия теории графов
Теория графов основывается на нескольких фундаментальных понятиях. В этом разделе мы рассмотрим их детально и приведём примеры, чтобы вы лучше усвоили материал.
Граф — это математическая структура, состоящая из двух множеств: множества вершин и множества ребер . Формально граф записывается как
, где:
- — множество вершин, представляющих объекты или сущности ,
- — множество ребер, представляющих связи или отношения между парами вершин.
Вершина — базовый элемент графа, обозначающий объект или сущность в рассматриваемой системе. Вершины обычно обозначаются заглавными буквами или числами . Степенью вершины обозначают количество рёбер, прилежащих к вершине.
Некоторые свойства вершин
Изолированная вершина. Вершина называется изолированной, если она не связана ни с одной другой вершиной, то есть из неё не выходит ни одно ребро. Изолированные вершины часто символизируют объекты без связей с остальной частью системы.
Висячая вершина. Вершина называется висячей, если из неё выходит ровно одно ребро. Такая вершина всегда является концом только одного ребра, которое соединяет её с другой вершиной, и может служить концом пути или периферийным элементом в графе.
Шарнир. Вершина графа называется шарниром, если её удаление приводит к потере связности графа (граф перестаёт быть единым целым и распадается на несколько частей). Шарнирные вершины являются критическими точками, связывающими части графа.
Ребро — соединение между двумя вершинами, отражающее существование связи или отношения между ними.
Некоторые свойства рёбер
Смежные рёбра. Два ребра называются смежными, если они имеют общую вершину. Это означает, что они делят одну и ту же вершину, сходясь в ней.
Кратные рёбра. Два ребра называются кратными, если они соединяют одну и ту же пару вершин. Такие рёбра позволяют моделировать множественные связи между одними и теми же объектами в графе.
Направленные рёбра. Ребро называется направленным, если оно имеет определённое направление из одной вершины в другую. Такое ребро соединяет упорядоченную пару вершин и направление указывает, из какой вершины ребро выходит и в какую входит. Направленные рёбра позволяют моделировать асимметричные отношения между вершинами.
Петля. Так называют ребро, которое соединяет вершину с самой собой. В таком случае оба конца ребра совпадают с одной и той же вершиной.
Мост. Мостом называется такое ребро графа, удаление которого приводит к увеличению числа компонент связности графа. Иными словами, после удаления моста граф становится менее связным.
Визуализируем понятия на двух графах.
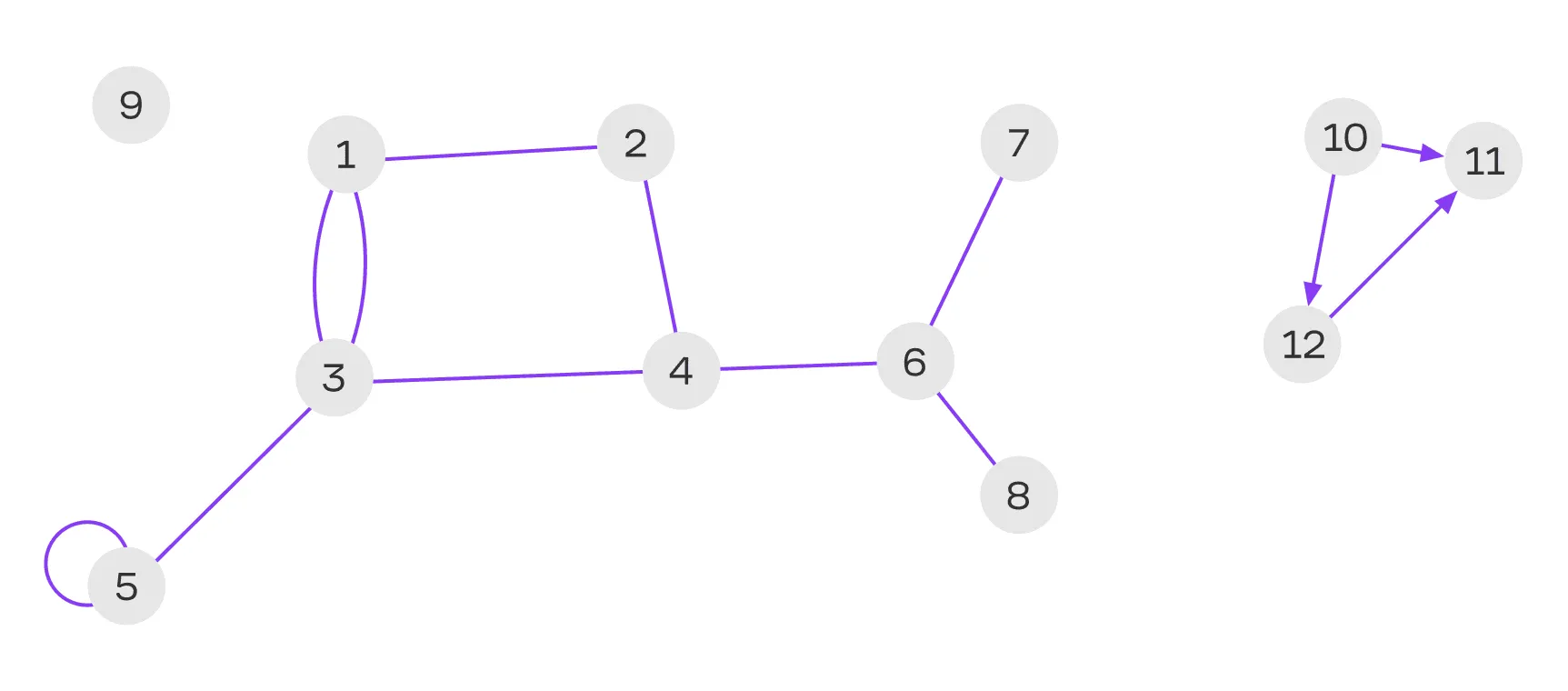
Первый граф можно представить как сеть гиперссылок между веб-страницами: каждая вершина соответствует отдельной странице, а ребро указывает на существование ссылки между ними. В этой модели страница 5 содержит ссылку на саму себя (петля), страницы 1 и 3 имеют по две взаимные ссылки друг на друга (кратное ребро), а страница 9 полностью изолирована — на неё нет ссылок, и она сама ни на кого не ссылается.
Второй граф можно представить как граф финансовых транзакций между тремя людьми — как они переводили друг другу деньги.
Прежде чем двинуться дальше, обратите внимание на визуализацию свойств рёбер и вершин этих графов:
- Петля — ребро 5–5.
- Кратное ребро — 1–3.
- Мост — ребро 4–6.
- Направленные рёбра — 10–11–12.
- Шарниры — вершины 3, 4, 6.
- Висячие вершины — 7, 8.
- Изолированная вершина — 9.
Двинемся дальше. К фундаментальным понятиям также относятся инцидентность и смежность. Они описывают отношения между вершинами и рёбрами в графе.
Вершина и ребро считаются инцидентными, если это ребро соединяет данную вершину с какой-либо другой вершиной.
- Инцидентное (прилежащее) ребро: ребро, которое соединяет данную вершину с другой вершиной.
- Инцидентная (прилежащая) вершина: вершина, которая является концом данного ребра.
Здесь важно отметить, что инцидентность относится исключительно к паре «вершина — ребро». Это означает, что ребро инцидентно своим конечным вершинам и каждая вершина инцидентна всем рёбрам, которые к ней прилегают.
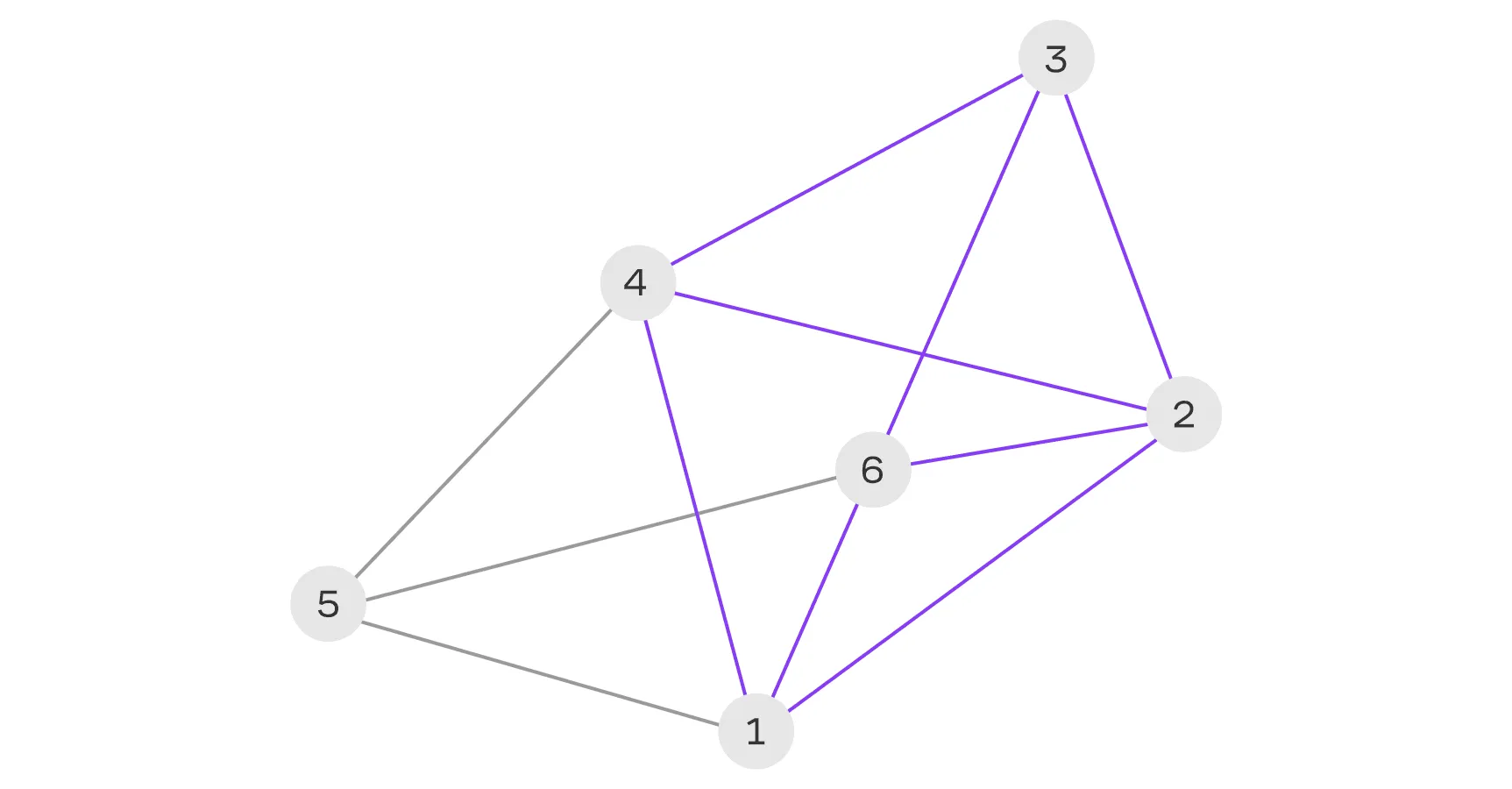
Это может звучать запутанно, разберём на примере. Посмотрите на граф:
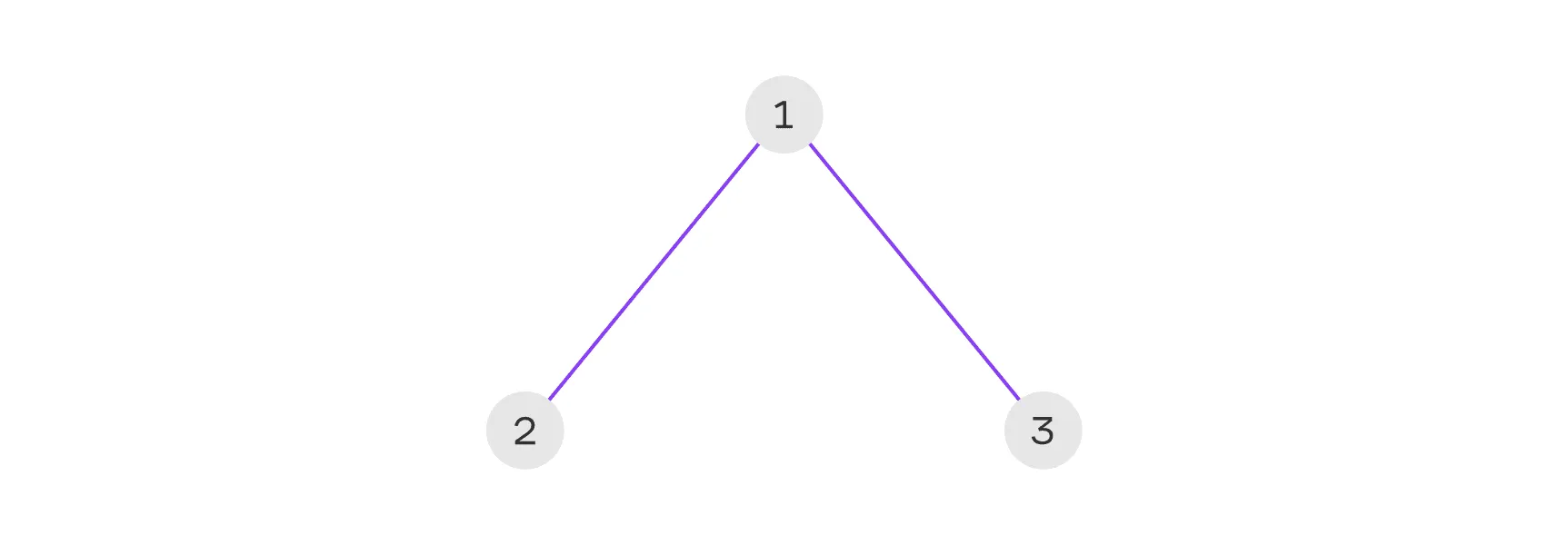
На этом графе:
- вершины 1 и 2 инцидентны ребру 1–2;
- вершины 1 и 3 инцидентны ребру 1–3;
- ребро 1–2 инцидентно вершинам 1 и 2;
- ребро 1–3 инцидентно вершинам 1 и 3.
Смежность, в свою очередь, описывает отношения между двумя вершинами или двумя рёбрами:
- Смежные вершины: две вершины считаются смежными, если они соединены общим ребром.
- Смежные рёбра: два ребра считаются смежными, если они имеют общую вершину, через которую соединяются.
На иллюстрации выше:
- вершины 1, 2 и 1, 3 — смежные;
- рёбра 1–2 и 1–3 — смежные.
Выходит, что инцидентность показывает связь между вершинами и рёбрами, а смежность помогает описать взаимное расположение вершин и рёбер в графе.
Ещё одно понятие — это путь. Путём называют последовательность вершин, в которой каждая пара соседних вершин соединена ребром. Например, в графе можно рассмотреть путь 1 — 3 — 2 — 5, где каждая вершина последовательно связана с предыдущей, ведь, чтобы следовать по пути, нужно двигаться только по существующим рёбрам графа, переходя от одной вершины к другой.
Путь называется простым, если все вершины, кроме начальной и конечной, попарно различны. Это ограничение означает, что в простом пути вершины не повторяются, что может быть важным при анализе графов, где нужно избегать циклов или замкнутых маршрутов.
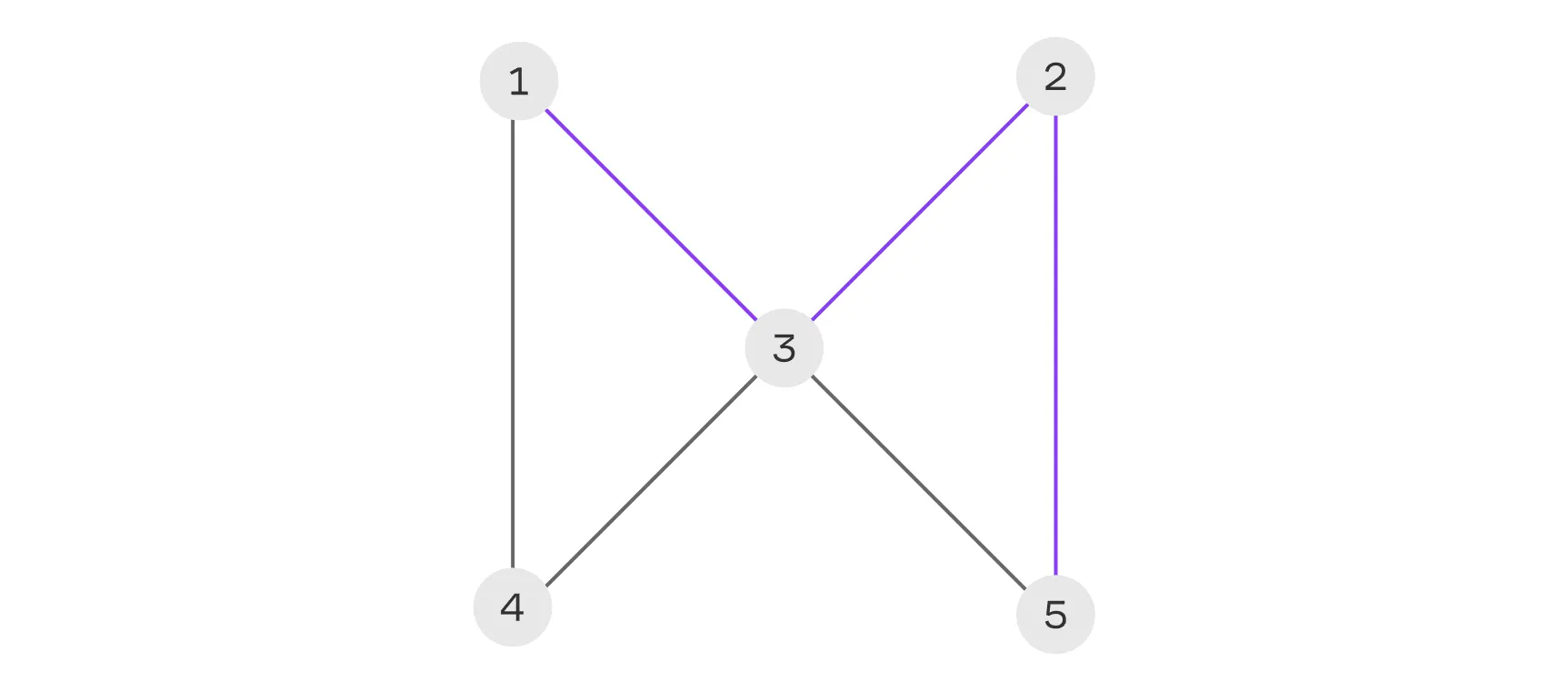
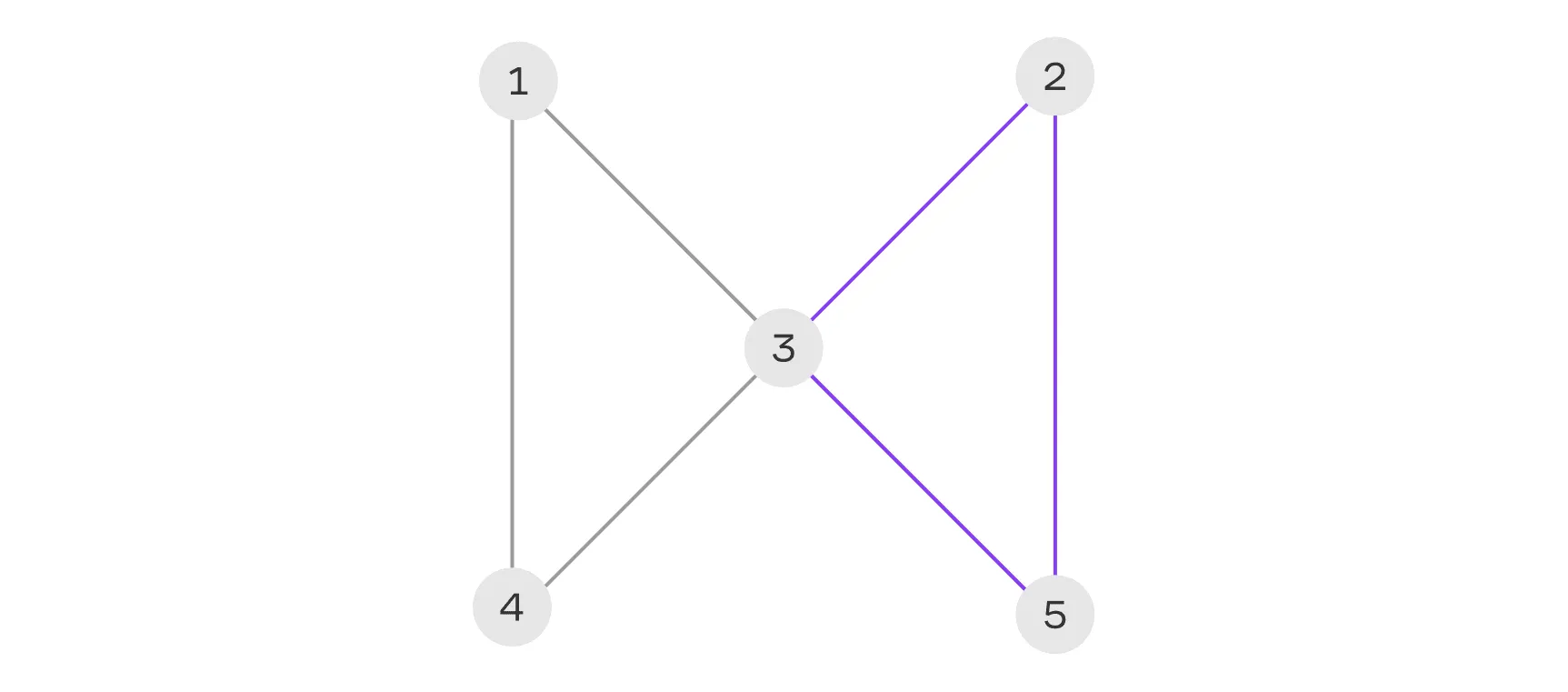
Цикл — это особый тип пути, который начинается и заканчивается в одной и той же вершине. Цикл можно записывать с любой вершины, с которой он начинается. Например, для цикла 2 — 3 — 5 — 2 начальная и конечная вершина совпадают, что делает его замкнутым.
Длина цикла — это количество рёбер, входящих в него, то есть в данном случае длина равна трём. Цикл называется простым, если в его составе все вершины и рёбра различны, за исключением начальной и конечной вершины, которые совпадают.
Продолжим. Граф называется полным, если все его вершины соединены между собой рёбрами. В таком графе для вершин максимальное количество рёбер равно в неориентированном графе и в ориентированном.
Подробнее о неориентированных и ориентированных графах мы поговорим в следующем параграфе. Пока просто запомните эти термины — они означают, есть в графе направленные рёбра или нет.
Плотный граф — это граф, в котором число рёбер близко к максимально возможному. Если же число рёбер значительно меньше максимального, граф называется разреженным.
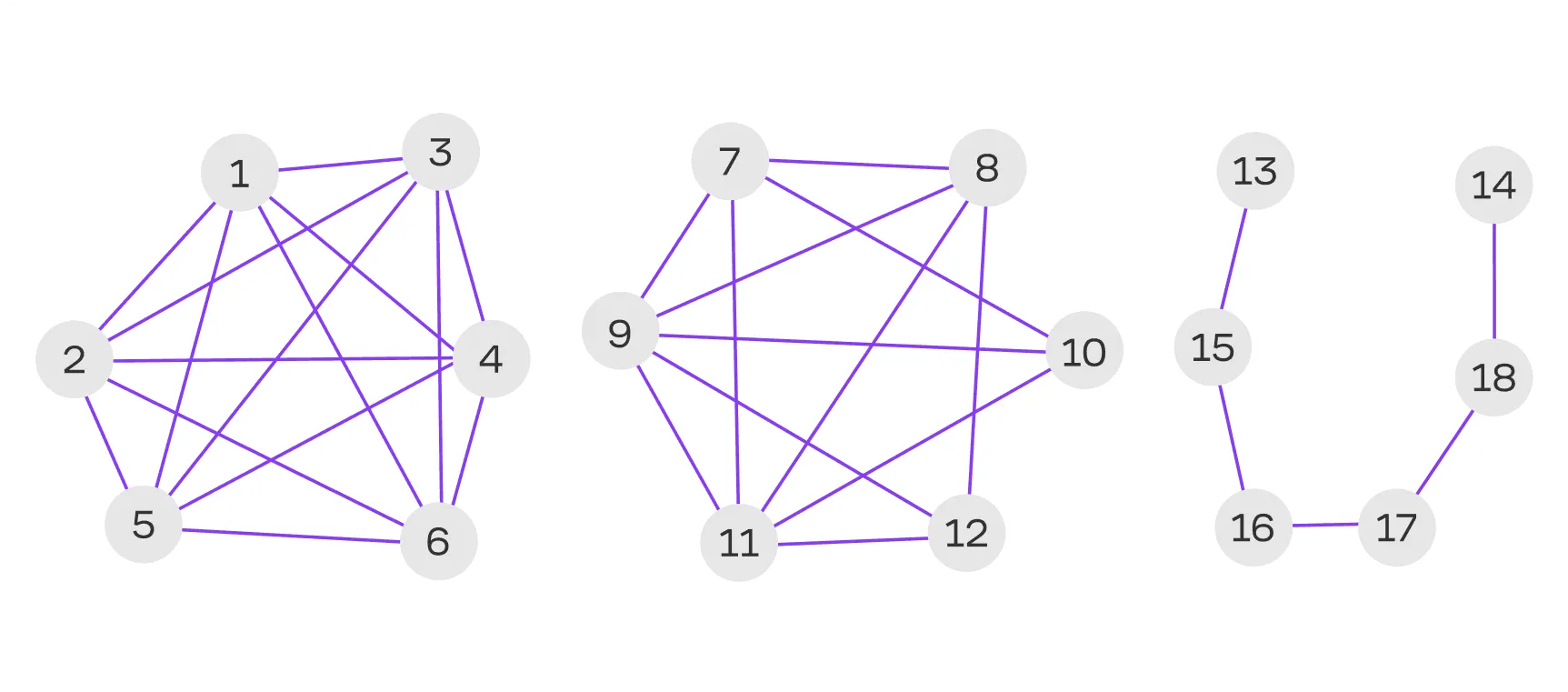
Кроме графов существуют и подграфы. Для начала дадим строгое описание, а потом поясним простыми словами.
Итак, подграф — это граф , вершины и ребра которого являются подмножествами вершин и ребер исходного графа . Если взять множество вершин графа как подмножество вершин исходного графа и множество ребер графа , соединяющих вершины из , как подмножество ребер графа , то такой граф называется подграфом графа .
Проще говоря, если в исходном графе удалить одну вершину вместе со всеми рёбрами, которые её соединяют с другими вершинами (то есть инцидентными ей рёбрами), то получившаяся структура будет подграфом исходного графа.
Подграф можно получить также, выделив несколько вершин и рёбра между ними в исходном графе, что создаст локализованное подмножество связей, сохраняющее структуру и свойства исходной модели. Это бывает полезно для анализа отдельных частей сложной системы, когда необходимо сконцентрироваться на конкретных элементах или изучить локальные закономерности без учёта остальной части графа.
С терминами разобрались. Теперь поговорим о том, как построить граф.
Как задать граф: способы представления
Графы можно описывать разными способами, у каждого из которых есть свои преимущества в зависимости от задачи.
Вот основные методы представления графов:
- список рёбер;
- матрица смежности;
- набор степеней вершин.
Рассмотрим их подробнее.
Список рёбер
Это один из самых простых способов описания графа, где он представляется как набор пар вершин, соединённых рёбрами.
В неориентированном графе рёбра не имеют направления и связь между двумя вершинами двусторонняя. Поэтому каждая пара вершин записывается только один раз. В ориентированном графе, напротив, рёбра имеют направление, что позволяет моделировать односторонние связи. В этом случае каждая пара вершин записывается с учётом направления и указанием, от какой вершины к какой идёт связь.
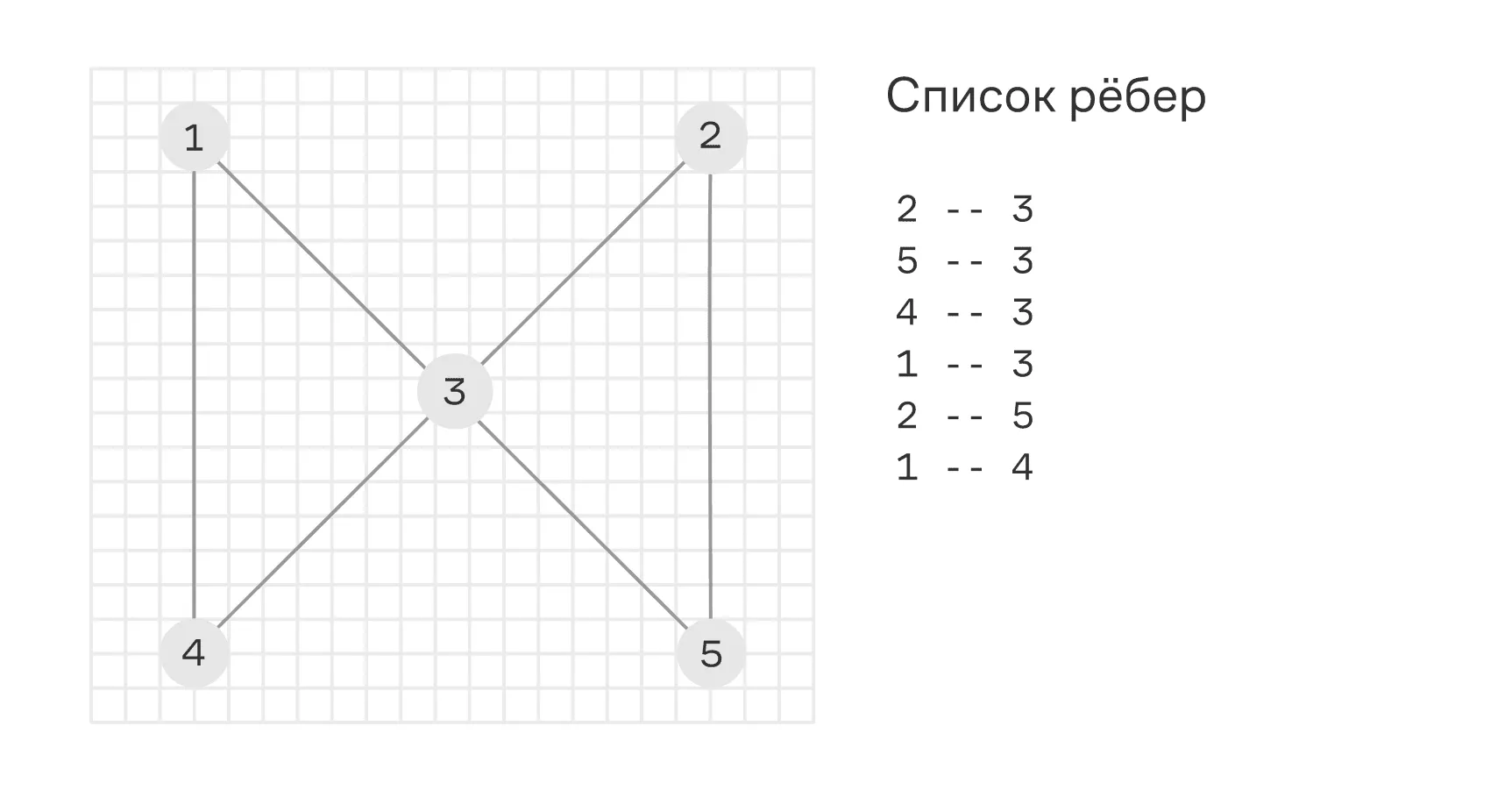
Преимущество представления графа списком рёбер заключается в простоте реализации этого подхода и удобстве его использования при небольшом количестве связей. Этот способ не требует большого объёма памяти и позволяет легко добавлять и удалять рёбра.
Однако он может оказаться неэффективным для задач, требующих частого обращения к информации о степени вершин или быстрого поиска путей между двумя вершинами.
Матрица смежности
Это ещё один способ описания графа, который использует квадратную матрицу, где строки и столбцы представляют вершины. Элемент матрицы равен , если вершины и соединены, и — в противном случае. В неориентированном графе такая матрица симметрична относительно главной диагонали.
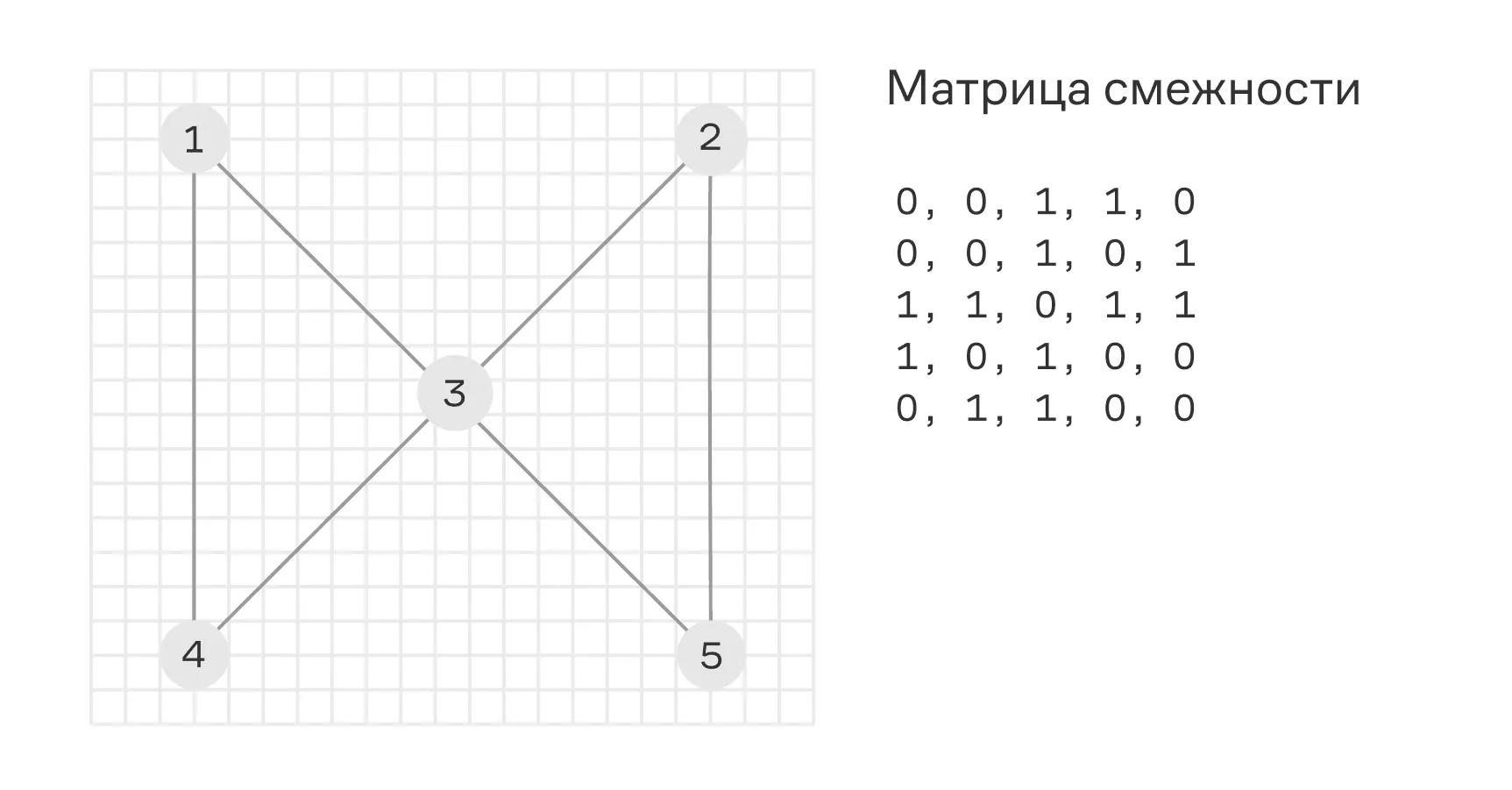
На визуализации выше матрица отображает, есть ли ребро между вершинами. Номера вершин — порядковые номера строк и колонок. То есть в строке №1 в колонках №3 и №4 стоят , что указывает на наличие рёбер, соединяющих вершину 1 с вершинами 3 и 4.
Если у рёбер графа есть вес, то в матрице смежности вместо можно записывать вес ребра, соединяющего вершины и . Это позволяет представлять взвешенные графы и учитывать интенсивность или стоимость связей между вершинами.
Помните, выше мы говорили про плотные и разреженные графы? Так вот, для разреженных графов матрица смежности становится менее эффективной, поскольку большинство её элементов равны нулю.
В таких случаях применяется альтернативное представление — список смежности, где для каждой вершины хранится список индексов вершин, с которыми она соединена. Этот метод значительно экономит память для разреженных графов.
Например, для графа с миллионом вершин, где вершины соединены по кругу, матрица смежности потребовала бы хранения элементов, тогда как список смежности потребует всего миллион записей, в каждой из которых будет всего два индекса.
Набор степеней вершин
В данном случае граф представляется списком степеней каждой вершины, то есть количеством рёбер, которые к ней прилегают. Этот метод удобен для анализа свойств графа, таких как плотность связей или распределение степеней вершин.
На иллюстрации ниже — два графа, в каждом из которых степень каждой вершины равна 2. Однако графы различны: в первом графе вершины соединены так, что образуются две отдельные компоненты, а во втором графе вершины соединены в замкнутый цикл.
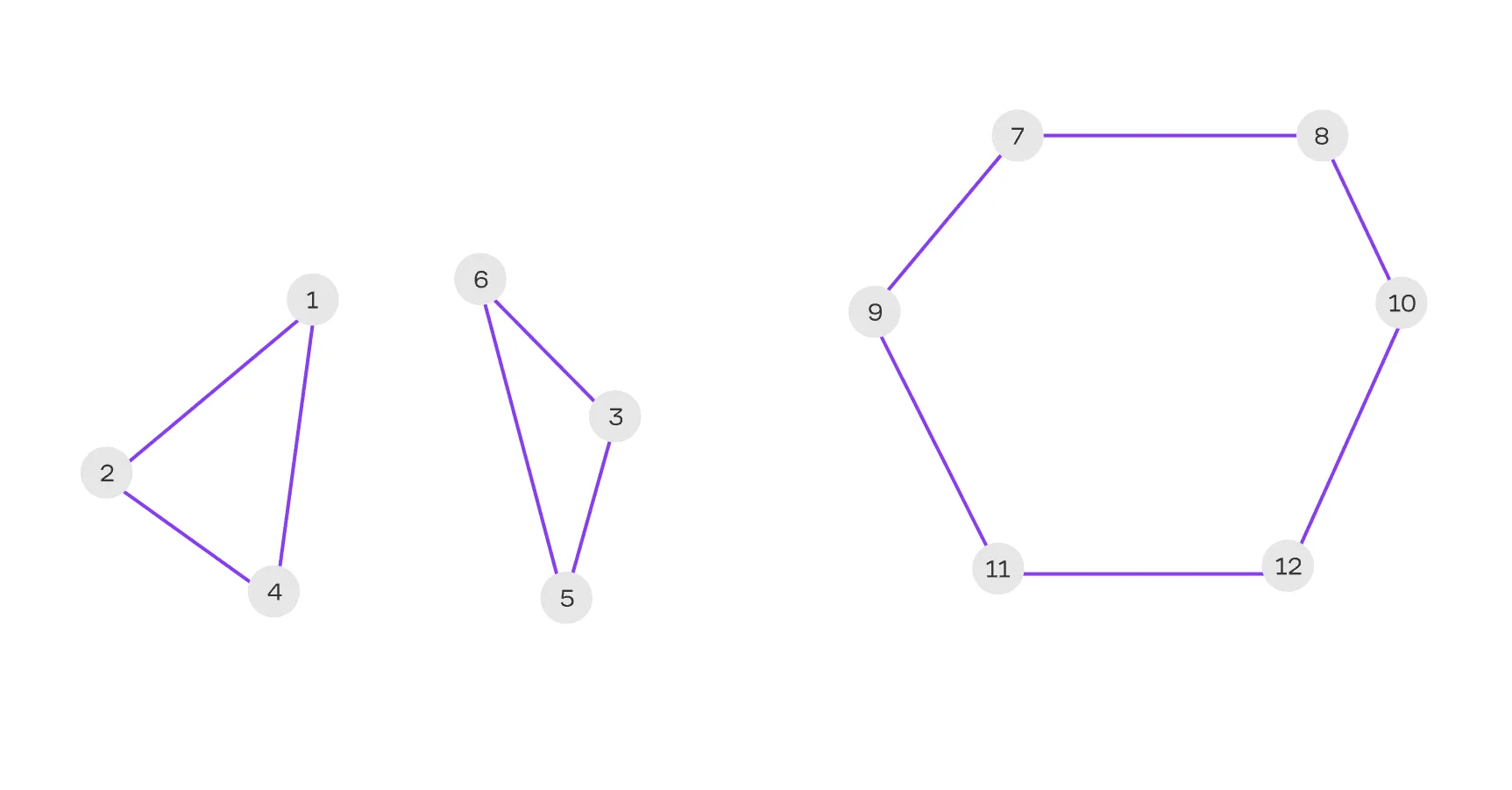
Основное преимущество представления графа через набор степеней — его компактность, особенно если у графа большое количество вершин и небольшое количество рёбер. Однако недостаток этого способа заключается в том, что он не позволяет точно восстановить структуру графа, так как множество различных графов могут иметь одинаковое распределение степеней вершин — как вы могли убедиться на иллюстрации выше.
Визуализация графов с помощью Python
Теперь, когда мы разобрались с основными понятиями теории графов и способами их описания, давайте перейдём к практическим примерам. В этом разделе мы познакомимся с библиотекой networkx, которая позволяет создавать и визуализировать графы разными способами.
Посмотрим на код:
1import networkx as nx
2import matplotlib.pyplot as plt
3import numpy as np
4
5# 1. Создание графа из списка рёбер
6edges = [(1, 2), (1, 3), (2, 3), (2, 4), (2, 5), (3, 5)]
7graph1 = nx.Graph()
8graph1.add_edges_from(edges)
9
10# 2. Создание графа из матрицы смежности
11adjacency_matrix = np.array([
12 [0, 1, 1, 0, 0],
13 [1, 0, 1, 1, 1],
14 [1, 1, 0, 0, 1],
15 [0, 1, 0, 0, 0],
16 [0, 1, 1, 0, 0]
17])
18graph2 = nx.from_numpy_array(adjacency_matrix)
19
20# 3. Создание графа из списка степеней вершин
21degrees = [4, 2, 2, 2, 2]
22graph3 = nx.random_degree_sequence_graph(degrees) # Создание случайного графа с заданными степенями
23
24# Визуализация графов
25plt.figure(figsize=(12, 4))
26
27plt.subplot(131)
28nx.draw(graph1, with_labels=True)
29plt.title('Из списка рёбер')
30
31plt.subplot(132)
32nx.draw(graph2, with_labels=True)
33plt.title('Из матрицы смежности')
34
35plt.subplot(133)
36nx.draw(graph3, with_labels=True)
37plt.title('Из списка степеней')
38
39plt.tight_layout()
40plt.show()
Вот что тут происходит:
- Мы создали три графа, используя разные методы описания графов.
- Затем
plt.subplotразделил график на три части для отображения всех трёх созданных графов. - Для визуализации мы использовали функцию
nx.draw(), которая рисует граф. - Также с помощью параметра
with_labels=Trueмы добавили метки к вершинам.
И вот какая получилась визуализация:
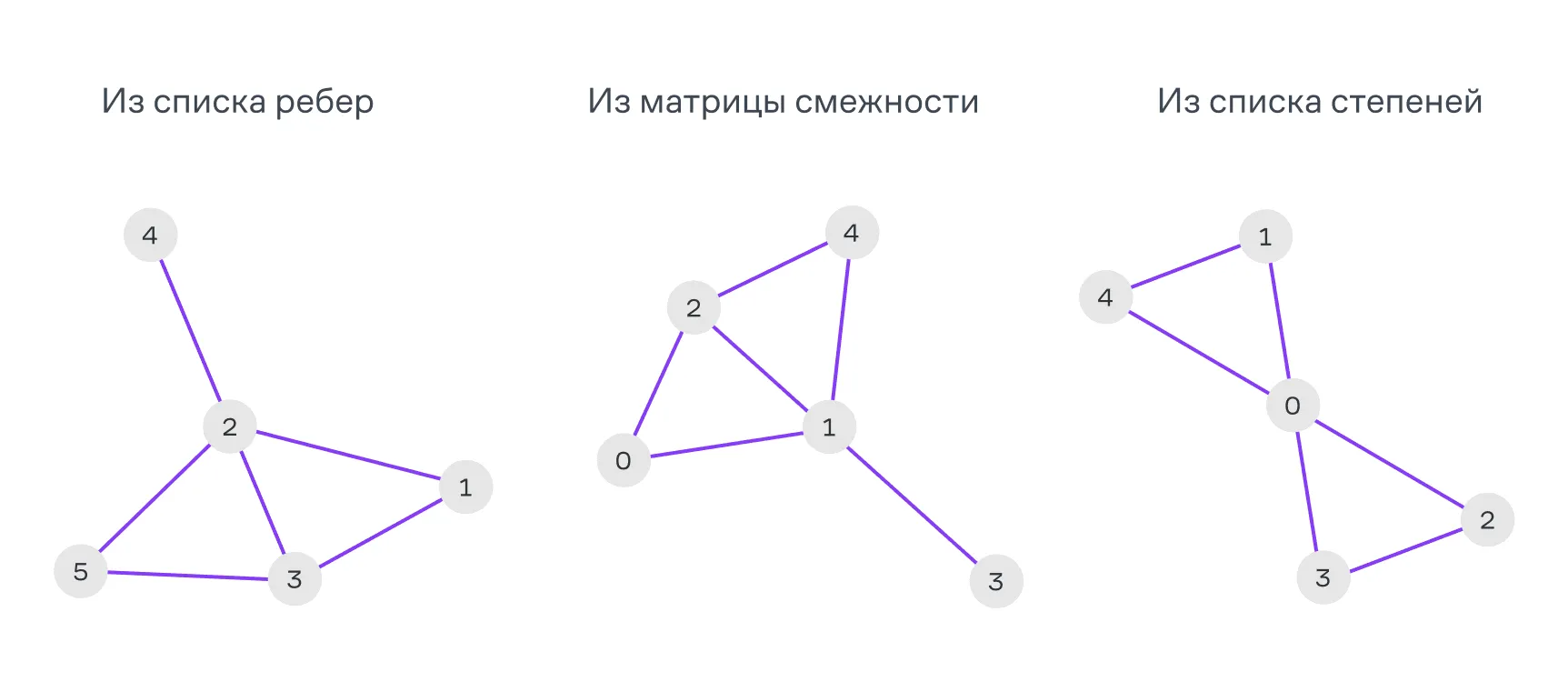
На этом всё — увидимся в следующем параграфе. А чтобы закрепить новые знания, рекомендуем вам пройти квиз и прорешать задачи для этого параграфа. Но прежде чем приступить к ним, советуем сперва взглянуть на небольшой гайд о том, как пользоваться системой проверки заданий.


