В этом параграфе мы вспомним матрицы и увидим, почему они — основа для большинства вычислительных операций в анализе данных и машинном обучении.
В работе с данными строки матрицы часто соответствуют объектам, а столбцы — признакам. В машинном обучении операции с матрицами лежат в основе линейных моделей, нейронных сетей и преобразований признаков.
Мы рассмотрим основные типы матриц, повторим ключевые операции, такие как сложение, умножение и транспонирование, и разберём их практическое применение — от загрузки датасетов с помощью pandas до реализации матричных операций в numpy.
Определение
Матрицей размера называется прямоугольная таблица из элементов, у которой строк и столбцов. Элементы матрицы обозначаются одной и той же буквой с двумя индексами, первый из которых — номер строки, а второй — номер столбца.
Например, элементы матрицы обычно обозначают как , где — номер строки, а — номер столбца.
Примеры интерпретации матриц:
-
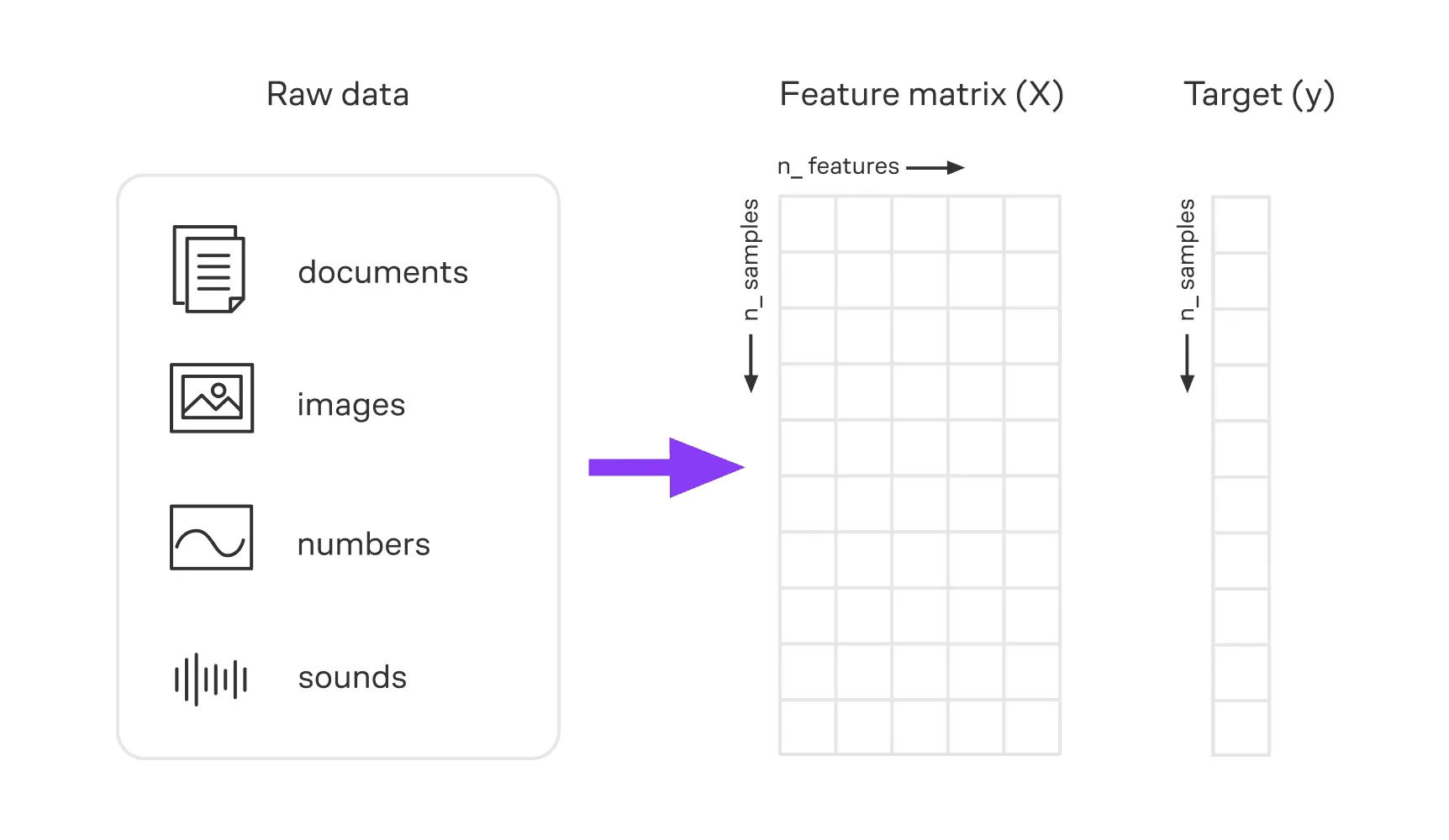
Табличные данные. B машинном обучении, когда у нас есть объектов и признаков, мы храним данные как матрицу .
-
Изображения. Каждый пиксель черно-белого изображения представляет собой число, которое отражает степень насыщенности цвета. Тогда изображение можно представить в виде сетки из пикселей — матрицы чисел.

Для наглядности матрицы яркостей исходное изображение было уменьшено до размера $28 х 28$
Типы матриц
Множество всех матриц с строками и столбцами будем обозначать через .
- Прямоугольная матрица. Матрица , у которой число строк не равно числу столбцов (). Пример:
- Квадратная матрица. Матрица , у которой число строк равно числу столбцов (). Пример:
- Диагональная матрица. Квадратная матрица, у которой все элементы вне главной диагонали равны нулю.
Главной диагональюназывают мысленную линию, которую можно провести через элементы , где . В примере ниже такая линия пройдёт через элементы
Пример:
- Верхнетреугольная матрица. Квадратная матрица, у которой все элементы ниже главной диагонали равны нулю, то есть при . А если все элементы выше главной диагонали равны нулю (), то такая матрица называется
нижнетреугольной.
Пример:
- Единичная матрица. Диагональная матрица, у которой все элементы главной диагонали равны 1. Часто обозначается как или . Пример:
Прежде чем перейти к рассказу о свойствах матриц, давайте ненадолго остановимся и поговорим, как создавать матрицы в Python — и с помощью каких инструментов.
Для работы с матрицами чаще всего используются библиотеки numpy, pandas и scipy. Выбор в пользу одной из них зависит от типа решаемой задачи. Но они в некотором смысле совместимы друг с другом, что позволяет использовать их одновременно.
Для удобства мы сравнили библиотеки в табличке:
|
Название |
Основная цель |
Применение |
Матрицы |
Преимущества |
|
NumPy |
Работа с n-мерными массивами и выполнение быстрых векторизованных операций. |
Базовая матричная математика, численные расчёты, подготовка данных для более высокоуровневых библиотек. |
Предоставляет объект |
Высокая производительность, обширный набор функций для базовой линейной алгебры, статистики, генерации случайных чисел и пр. |
|
Pandas |
Работа с табличными данными (например, данными из CSV, баз данных) с богатым набором средств для фильтрации, агрегации и анализа. |
Анализ и манипуляция данными, где важна структурированность и метаданные, а не только чистые числовые операции. |
Структуры |
Удобная индексация, возможность работы с разными типами данных в одном объекте, интеграция с другими источниками данных и мощные инструменты для группировки и агрегации. |
|
SciPy |
Предоставление расширенного набора алгоритмов для научных и инженерных вычислений. |
Решение сложных задач в области физики, инженерии, статистики и других областях, требующих специализированных методов обработки матриц и численных расчётов. |
Строится поверх NumPy, дополняя его более специализированными модулями, такими как |
Широкий спектр готовых к использованию алгоритмов, оптимизированных для научных задач, которые часто выходят за рамки базовых операций NumPy. |
Чтобы упростить вам задачу выбора, вот короткое и ёмкое саммари, когда и какую библиотеку применять:
- Если нужно работать с массивами и выполнять базовые матричные операции —
numpy. - Если задача — анализ табличных данных с метками и сложной агрегацией, то
pandas. - Если требуются более продвинутые методы обработки матриц, специализированные алгоритмы и работа с разрежёнными матрицами —
scipy.
Для начала рассмотрим, как выглядят матрицы в каждой из этих библиотек.
Матрицы в NumPy
1import numpy as np
2
3# Для создания матрицы с заданными значениями
4# используется функция `np.array()`, как и для векторов,
5# но, в отличие от векторов, матрицы могут быть многомерными
6
7A = np.array([[1, 2], [3, 4], [5, 6]]) # матрица размера 3x2
8print(A)
9
10# Output:
11# [[1 2]
12# [3 4]
13# [5 6]]
Также можно создавать специальные матрицы. Например, матрицу нулей заданного размера, используя функцию np.zeros() по аналогии с векторами (об этом мы говорили в предыдущем параграфе):
1O = np.zeros(shape=(3, 2))
2print(O)
3
4# Output:
5# [[0. 0.]
6# [0. 0.]
7# [0. 0.]]
Аналогично для матрицы единиц:
1E = np.ones(shape=(3, 2))
2print(E)
3
4# Output:
5# [[1. 1.]
6# [1. 1.]
7# [1. 1.]]
И для случайной матрицы:
1rng = np.random.default_rng()
2R = rng.random(shape=(3, 2))
3print(R)
4
5# Output:
6# [[0.47821453 0.28421059]
7# [0.2178972 0.07891322]
8# [0.63259903 0.4502506 ]]
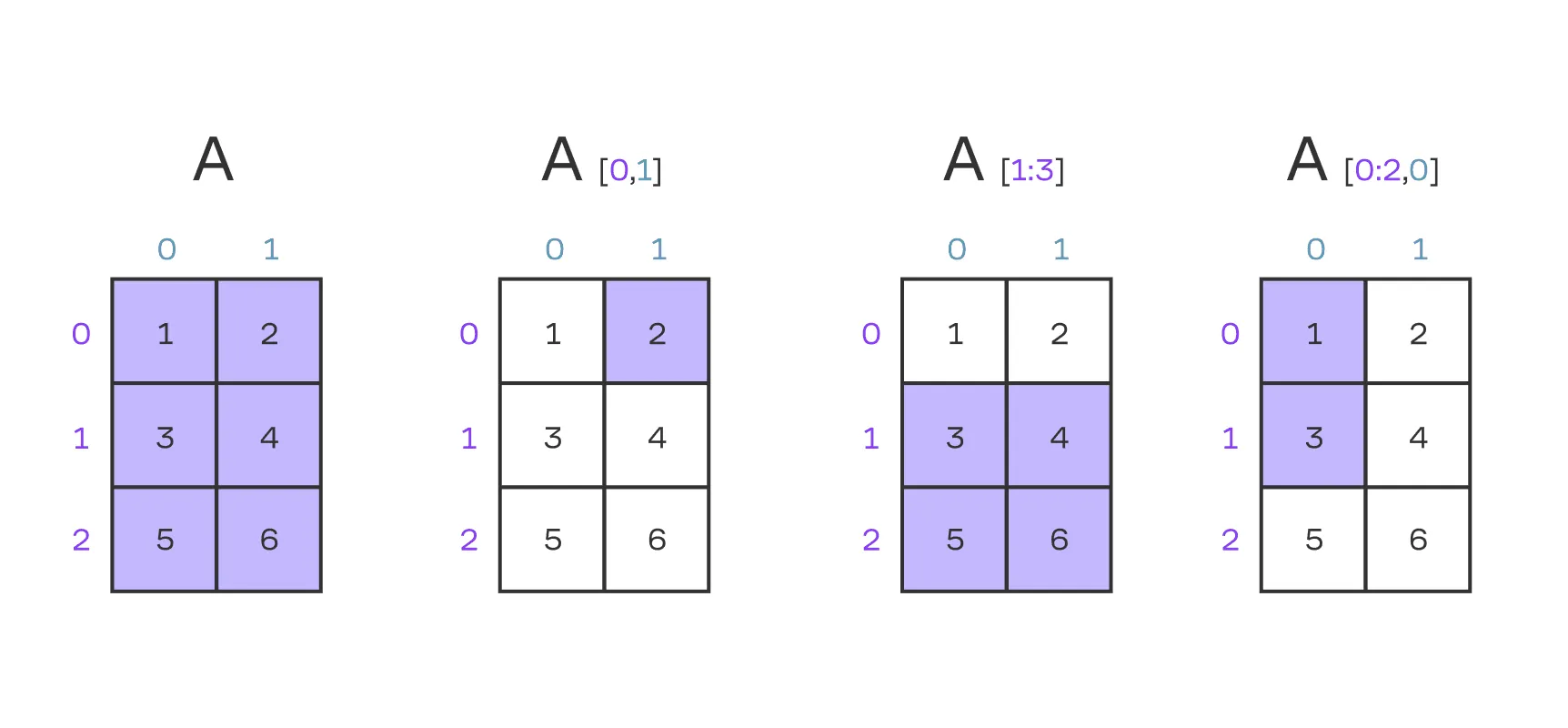
Также полезно знать, как индексируются матрицы:
1print(A[0, 1])
2print(A[1:3])
3print(A[0:2, 0])
4
5# Output:
6# 2
7# array([[3, 4],
8# [5, 6]])
9# array([1, 3])
Теперь рассмотрим, как создавать матрицы в pandas.
Матрицы в Pandas
1import pandas as pd
2
3# Создаём матрицу в виде списка списков
4A = [
5 [1, 2],
6 [3, 4],
7 [5, 6]
8]
9
10# Преобразуем список списков в DataFrame и задаём имена столбцов
11df = pd.DataFrame(A, columns=["Column1", "Column2"])
12
13# Выводим DataFrame (матрицу)
14print(df)
15
16# Output:
17# Column1 Column2
18# 0 1 2
19# 1 3 4
20# 2 5 6
На первый взгляд кажется, что больших отличий с numpy нет. Но использовать pandas намного удобнее, когда мы работаем с табличными данными, так как мы можем более гибко манипулировать ими.
1import pandas as pd
2
3# Группировка и агрегация данных по категориальному признаку
4# Допустим, у нас есть данные о зарплатах по отделам
5data_group = {
6 'Отдел': ['HR', 'IT', 'HR', 'IT', 'HR'],
7 'Зарплата': [40000, 70000, 45000, 72000, 42000]
8}
9df_group = pd.DataFrame(data_group)
10# Группируем по столбцу 'Отдел' и
11# вычисляем среднюю зарплату в каждом отделе
12grouped = df_group.groupby('Отдел').mean()
13print("Средняя зарплата по отделам:")
14print(grouped)
15
16# Output:
17# Средняя зарплата по отделам:
18# Зарплата
19# Отдел
20# HR 42333.333333
21# IT 71000.000000
Библиотека pandas — очень мощный инструмент, используемый в анализе данных, и в рамках линейной алгебры мы будем иногда обращаться к нему. Теперь рассмотрим библиотеку scipy.
Матрицы в SciPy
Выше мы выделили пять типов матриц, но на практике часто встречается ещё один тип матриц — разрежённые.
Разрежённая матрица — это матрица, в которой большая часть элементов равна нулю. В таких случаях хранение и обработка исходной матрицы может быть неэффективной по памяти и времени. Для разрежённых матриц используются специальные форматы хранения, которые сохраняют только ненулевые элементы и их индексы.
Библиотека scipy как раз содержит методы для хранения таких матриц и работы с ними. Далее мы ещё более плотно поработаем с такими матрицами, а сейчас лишь поймём, как их можно задавать. Создадим разрежённую матрицу в формате COO (Coordinate format), он позволяет задавать ненулевые элементы матрицы через координаты (индексы строк и столбцов) и значения.
1import numpy as np
2from scipy.sparse import coo_matrix
3
4# Определяем ненулевые элементы: их значения и позиции (строки и столбцы)
5rows = np.array([0, 1, 2, 0])
6cols = np.array([1, 2, 0, 2])
7data = np.array([10, 20, 30, 40])
8
9# Создаём матрицу размером 3x3
10sparse_coo = coo_matrix((data, (rows, cols)), shape=(3, 3))
11
12print("Исходная матрица:")
13print(sparse_coo.toarray())
14
15print("\nРазрежённая матрица в формате COO:")
16print(sparse_coo)
17
18# Output:
19# Исходная матрица:
20# [[ 0 10 40]
21# [ 0 0 20]
22# [30 0 0]]
23
24# Разрежённая матрица в формате COO:
25# (0, 1) 10
26# (1, 2) 20
27# (2, 0) 30
28# (0, 2) 40
Важно заметить, что NumPy, Pandas и SciPy — это взаимодополняющие инструменты, где объект ndarray служит общей основой.
1import numpy as np
2import pandas as pd
3from scipy.sparse import coo_matrix
4
5# Шаг 1: Создаём базовый NumPy array
6data = np.array([[0, 0, 3],
7 [4, 0, 0],
8 [0, 5, 6]])
9print("Исходный NumPy array:")
10print(data)
11
12# Шаг 2: Преобразуем NumPy array в разрежённую матрицу в формате COO
13sparse_matrix = coo_matrix(data)
14print("\nРазрежённая матрица (COO формат):")
15print(sparse_matrix)
16
17# Шаг 3: Преобразуем разрежённую матрицу обратно в плотный NumPy array
18dense_array = sparse_matrix.toarray()
19print("\nПлотный NumPy array, полученный из разрежённой матрицы:")
20print(dense_array)
21
22# Шаг 4: Создаём DataFrame Pandas на основе плотного массива
23df = pd.DataFrame(dense_array, columns=['Column1', 'Column2', 'Column3'])
24print("\nDataFrame (Pandas):")
25print(df)
26
27# Output:
28# Исходный NumPy array:
29# [[0 0 3]
30# [4 0 0]
31# [0 5 6]]
32
33# Разрежённая матрица (COO формат):
34# (0, 2) 3
35# (1, 0) 4
36# (2, 1) 5
37# (2, 2) 6
38
39# Плотный NumPy array, полученный из разрежённой матрицы:
40# [[0 0 3]
41# [4 0 0]
42# [0 5 6]]
43
44# DataFrame (Pandas):
45# Column1 Column2 Column3
46# 0 0 0 3
47# 1 4 0 0
48# 2 0 5 6
В задачах линейной алгебры использование библиотеки NumPy выглядит более удобным и эффективным, так как данная библиотека предоставляет оптимизированные функции для работы с многомерными массивами. В то время как Pandas и SciPy ориентированы на структурированный анализ данных и специализированные численные методы соответственно.
Также полезно понимать, что в NumPy можно работать не только с векторами и матрицами, но и с объектами произвольного размера, которые называются тензорами.
Тензор — это математический объект, который обобщает понятия скаляров, векторов и матриц. Можно представить его как многомерный массив чисел, где:
- тензор нулевого порядка — это скаляр (одно число);
- тензор первого порядка — это вектор (одномерный массив);
- тензор второго порядка — это матрица (двумерный массив);
- тензоры более высокого порядка — это массивы с тремя и более индексами.
Отлично, с этим разобрались. Теперь поговорим про операции над матрицами.
Операции над матрицами
Сложение
Пусть , тогда сумма определяется поэлементно, то есть , где , или
Пример:
Важно: складывать можно только матрицы одинакового размера. При этом на практике можно выполнять арифметические операции над объектами уже разного размера, автоматически «расширяя» меньший объект так, чтобы его размеры стали совместимы с размерами большего объекта.
То есть мы «выравниваем» размеры матриц, чтобы они по факту стали одинакового размера. В NumPy данный механизм называетсяbroadcasting.
Умножение на скаляр
Пусть и , тогда произведение определяется поэлементно, то есть , где , или
Пример:
Умножение
Пусть и , тогда произведение определяется как , где , или
Проще говоря, чтобы получить значение , нужно из матрицы взять -ю строку, а из матрицы — -й столбец и скалярно их перемножить.
Важно: произведение двух матриц определено только тогда, когда их размеры согласованы, а именно когда число столбцов первой матрицы равно числу строк второй.
Пример:
Вычисление по шагам
- Вычислим :
- Вычислим :
- Вычислим :
- Вычислим :
В нейронных сетях, особенно в полносвязных (fully-connected), каждый слой можно рассматривать как матричное преобразование.
Например, если на вход слоя приходит вектор размерности , он умножается на матрицу весов и складывается со смещением (bias) , в результате чего получается новый вектор размерности .
Схематично:
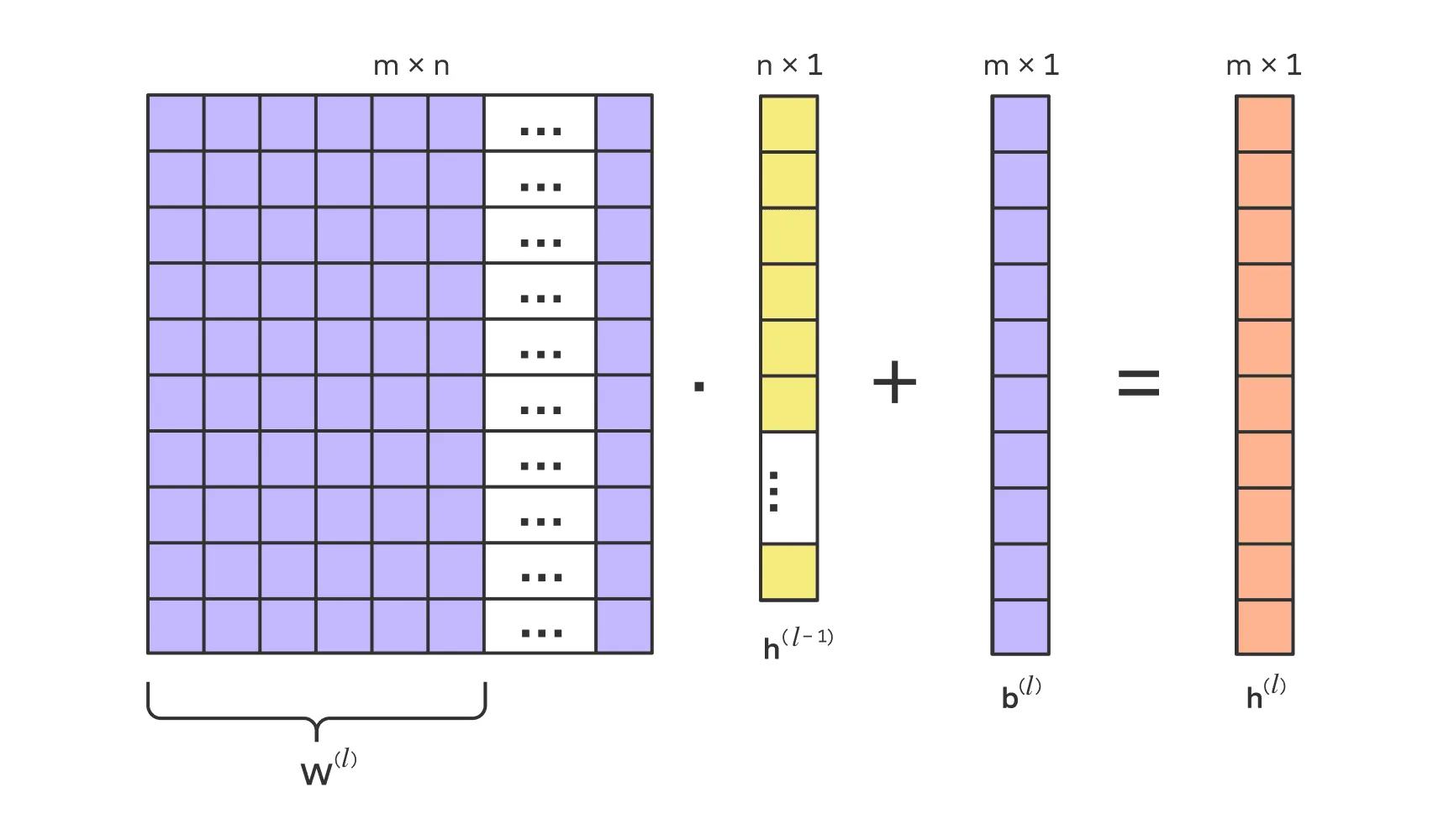
Таким образом, в нейронных сетях матричные операции играют ключевую роль при обработке данных, где веса и смещения (bias) обновляются в процессе обучения, что позволяет сети обучаться на данных.
В процессе обучения для эффективного вычисления и обновления параметров используются специализированные алгоритмы и библиотеки глубокого обучения (например, PyTorch, TensorFlow), которые могут распараллеливать вычисления на графических процессорах (GPU), значительно ускоряя обработку матриц.
Интересные особенности матричного умножения
После освоения базовых операций над матрицами становится ясно, что их умножение обладает рядом уникальных свойств, отличающих его от обычного умножения чисел. Давайте рассмотрим эти свойства.
-
Умножение матриц некоммутативно.
-
Пусть и , при этом . Тогда определено произведение , но произведение уже не определено из-за несогласованности размеров матриц.
-
Пусть и . Тогда определено как произведение , так и . Однако матрицы и имеют разные размеры, следовательно, не могут быть одинаковыми.
-
Пусть . Тогда определено как произведение , так и , и у матриц совпадают размеры. Однако даже это не даёт им быть одинаковыми. Пример:
-
-
В матрицах есть
делители нуля.
То есть существуют ненулевые матрицы и , такие, что: . Пример: -
В матрицах есть
нильпотенты.
То есть можно найти такую ненулевую матрицу , что . Пример:
Транспонирование
Пусть , тогда определим транспонированную матрицу следующим образом:
То есть строками транспонированной матрицы служат столбцы матрицы , а столбцами — строки матрицы . На уровне элементов это выглядит так: .
Примеры:
Как вы думаете, чему равно ?
Ответ (не открывайте сразу; сначала подумайте сами!)
- После первого транспонирования получаем матрицу , где элементы становятся .
- После второго транспонирования получаем матрицу , где элементы становятся .
- Таким образом:
След матрицы
След — это сумма диагональных элементов матрицы. Пусть , тогда определим след матрицы так:
Отметим важные свойства следа матрицы:
- Для любых матриц верно .
- Для любой матрицы и выполнено .
- Для любых матриц и выполнено .
Третье свойство особо важно в анализе данных и линейной алгебре. Например, при упрощении выражений в оптимизационных задачах: регуляризация в линейной регрессии или оценка суммы квадратов через произведение матриц.
Пример №1
Посмотрим на регуляризацию в классической постановке линейной регрессии. В текущем примере мы продемонстрируем, как L2-регуляризация (или ridge-регрессия), которая добавляет штраф за большие значения весов, используется в контексте матричных выражений и как свойство следа помогает упрощать записи для аналитических и численных методов.
Пусть:
- — матрица признаков (строки соответствуют объектам, столбцы — признакам),
- — вектор весов (параметры модели),
- — вектор целевых значений.
Тогда вектор предсказаний:
При L2-регуляризации к функционалу суммы квадрата ошибки добавляется член :
где .
Иногда, когда эта регуляризация записывается в матричном (или «следовом») виде, мы можем встретить выражения наподобие:
и снова свойство позволяет объединять такие слагаемые с другими матричными выражениями в удобной форме. Например, при анализе функций потерь или выведении их градиентов.
Пример №2
Иногда (особенно в задачах, связанных с статистикой и PCA) появляется сумма вида где — строки некоторой матрицы .
Записав целиком, мы можем перейти к выражениям наподобие:
А затем использовать:
Здесь чётко видно, как перестановка факторов под следом (из-за ) упрощает анализ ковариационных матриц или при поиске оптимальных .
Данное свойство также крайне удобно при дифференцировании «следовых» выражений. В теории оптимизации часто встречаются производные вида , а благодаря свойству мы можем свободно переставить множители, что даёт в итоге более лаконичную формулу для градиента:
Это упрощение позволяет легко получать результат без разворачивания сумм по индексам, что крайне полезно в машинном обучении и методах оптимизации, особенно при работе с большими матрицами и векторно-ориентированными библиотеками вроде pytorch, numpy и другими.
После того как мы изучили, как задаются матрицы и выполняются над ними операции (сложение, умножение, транспонирование и так далее), рассмотрим свойства этих операций. Они определяют их алгебраическую структуру и играют ключевую роль в решении как теоретических, так и практических задач.
Свойства операций
- Ассоциативность сложения
для любых . - Существование нейтрального элемента для сложения
Существует единственная матрица , такая, что: для всех . Такая матрица целиком заполнена нулями. - Коммутативность сложения
для любых . - Наличие обратного по сложению
Для любой матрицы существует матрица , такая, что: . Такая матрица единственная и состоит из элементов . - Ассоциативность умножения
Для любых матриц и верно . - Существование нейтрального элемента для умножения
Для каждого существует единственная матрица , такая, что для любой матрицы верно . У такой матрицы , а . - Дистрибутивность умножения относительно сложения
Для любых матриц и верно (. Аналогично для любых и верно . - Умножение на числа ассоциативно
Для любых и любой матрицы верно . Аналогично для любого и любых и верно . - Умножения на числа дистрибутивно относительно сложения матриц и относительно сложения чисел
Для любых и верно . Аналогично для любого и верно . - Умножение на скаляр нетривиально
Если , то для любой матрицы верно . - Умножение на скаляр согласовано с умножением матриц
Для любого и любых и верно . - Транспонирование согласовано с суммой
Для любых матриц верно . - Транспонирование согласовано с умножением на скаляр
Для любой матрицы и любого верно . - Транспонирование согласовано с умножением
Для любых матриц верно .
А теперь мы можем посмотреть, как операции над матрицами реализованы в Python.
Операции над матрицами в Python
Обычно для выполнения арифметических операций с матрицами они должны быть одинакового размера. Однако, как мы сказали выше, в NumPy можно оперировать матрицами различного размера за счёт механизма broadcasting. При этом действуют следующие правила:
- Если объекты имеют разное число измерений, к объекту с меньшим числом измерений добавляются измерения длины 1 слева.
- Для каждого соответствующего измерения длины должны совпадать или одна из них должна быть равна 1.
Например, если один тензор имеет размер , а другой , то размер первого тензора при операциях будет приведён к . При этом если их сложить, то размер получившегося тензора будет уже : по каждому из измерений тензоров мы взяли максимальное значение длины. Это позволяет писать компактный и эффективный код, не прибегая к явному копированию данных для согласования размеров объектов.
Рассмотрим несколько примеров.
1import numpy as np
2
3r = 4 # скаляр
4v = np.arange(3) # вектор
5a = np.arange(9).reshape(3, 3) # матрица
6
7# Сумма скаляра и вектора
8print(r + v)
9
10# Сумма вектора и матрицы
11print(v + a)
12
13# Сумма векторов разного размера
14print(v.reshape(3, 1) + v)
15
16# Output:
17# array([4, 5, 6])
18
19# array([[ 0, 2, 4],
20# [ 3, 5, 7],
21# [ 6, 8, 10]])
22
23# array([[0, 1, 2],
24# [1, 2, 3],
25# [2, 3, 4]])
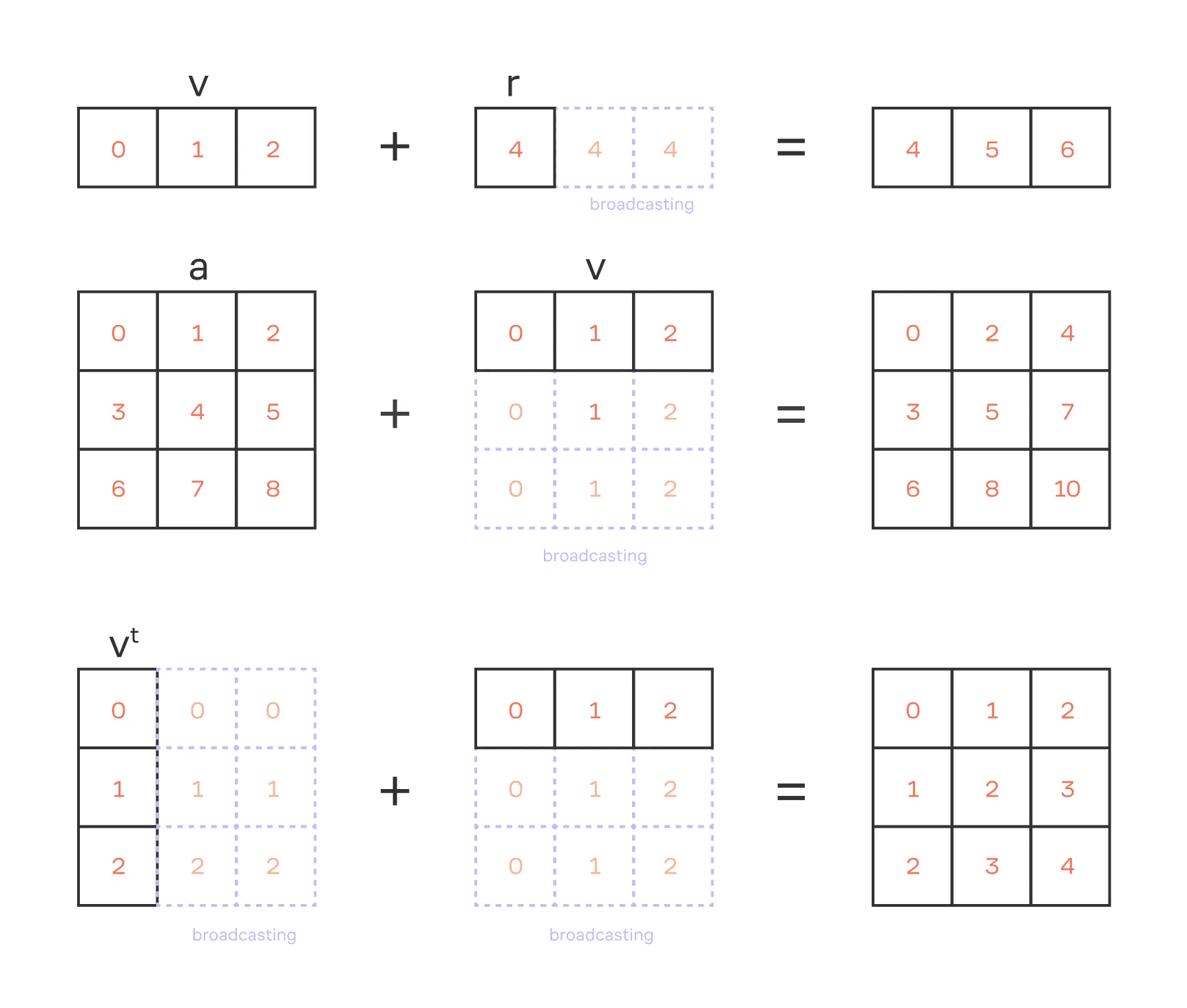
Иллюстрация механизма broadcasting
Отдельно стоит рассмотреть, как устроено умножение матриц и векторов в NumPy. Можно выделить два основных способа умножения, которые выглядят похоже, но выполняют совершенно разные операции.
1.Поэлементное умножение (*)
Оператор * выполняет поэлементное умножение двух тензоров, которые должны иметь совместимые размеры (согласно правилам broadcasting). То есть если у вас есть два тензора одинакового размера (или они могут быть «расширены» до одного размера), то операция a * b перемножает соответствующие элементы:
Пример:
1import numpy as np
2
3# Задаём два вектора
4a = np.array([1, 2, 3])
5b = np.array([4, 5, 6])
6
7# Поэлементное умножение: возвращает массив тех же размеров
8elementwise = a * b
9print("Поэлементное умножение a * b:")
10print(elementwise)
11
12# Задаём две матрицы
13A = np.array([[1, 2], [3, 4]])
14B = np.array([[5, 6], [7, 8]])
15
16# Поэлементное умножение: перемножаются соответствующие элементы
17elementwise = A * B
18print("Поэлементное умножение A * B:")
19print(elementwise)
20
21# Output:
22# Поэлементное умножение a * b:
23# [ 4 10 18]
24# Поэлементное умножение A * B:
25# [[ 5 12]
26# [21 32]]
2.Матричное умножение (@ или np.dot/np.matmul)
Оператор @ (введённый в Python 3.5) предназначен для матричного умножения согласно правилам линейной алгебры. При этом для двух векторов и операция a @ b вычисляет их скалярное произведение:
А для матриц и (при условии, что число столбцов равно числу строк ) результатом будет матрица , где:
Пример:
1import numpy as np
2
3# Задаём два вектора
4a = np.array([1, 2, 3])
5b = np.array([4, 5, 6])
6
7# Матричное умножение: возвращает скаляр
8dot_product = a @ b # Результат: 1*4 + 2*5 + 3*6 = 32
9print("Скалярное произведение a @ b:")
10print(dot_product)
11
12# Задаём две матрицы
13A = np.array([[1, 2], [3, 4]])
14B = np.array([[5, 6], [7, 8]])
15
16# Матричное умножение (стандартное): используется оператор @
17matrix_product = A @ B
18print("Матричное умножение A @ B:")
19print(matrix_product)
20
21# Output:
22# Скалярное произведение a @ b:
23# 32
24# Матричное умножение A @ B:
25# [[19 22]
26# [43 50]]
Если массивы имеют более двух измерений, оператор * всё равно делает поэлементное умножение, а @ или np.matmul применяют матричное умножение к последним двум осям с поддержкой broadcasting для остальных осей.
1import numpy as np
2
3# Создаём два 3D массива (тензора)
4X = np.random.rand(2, 3, 4)
5Y = np.random.rand(2, 4, 5)
6
7# np.matmul (или оператор @) умножает X и Y по последним двум измерениям
8matmul_result = X @ Y
9print("Форма результата матричного умножения:", matmul_result.shape)
10
11# Поэлементное умножение (*) здесь не сработает напрямую,
12# т. к. размеры (2,3,4) и (2,4,5) несовместимы для
13# поэлементного умножения без явного преобразования.
14elementwise_result = X * Y
15
16# Output:
17# Форма результата матричного умножения: (2, 3, 5)
18# ValueError: operands could not be broadcast together with shapes (2,3,4) (2,4,5)
Теперь потренируемся с операциями над матрицами.
Ранее мы уже видели, как с помощью матрицы задаётся изображение. Давайте рассмотрим на наглядном примере, как операции с матрицами могут влиять на практический результат. Для этого возьмём изображение и определённым образом изменим его матрицу.
1import numpy as np
2from PIL import Image
3import matplotlib.pyplot as plt
4
5# Путь к изображению
6image_path = "image.jpg"
7
8# Считываем изображение и переводим его в оттенки серого
9image = Image.open(image_path).convert("L")
10image_np = np.array(image, dtype=float)
11
12# Фильтр понижения яркости: отнимаем константу от всех элементов матрицы
13brightness_offset = -50
14result_brightness = np.clip(image_np + brightness_offset, 0, 255)
15
16# Фильтр инверсии: вычисляем отрицательное изображение
17result_inversion = 255 - image_np
18
19# Пороговая фильтрация: если значение пикселя больше порога, ставим 255, иначе 0
20threshold = 128
21result_threshold = np.where(image_np > threshold, 255, 0)
22
23# Создаём фигуру с заданными параметрами
24fig, axes = plt.subplots(2, 2, figsize=(15, 8), dpi=200)
25
26axes[0, 0].imshow(image_np, cmap='gray')
27axes[0, 0].set_title("Исходное изображение")
28axes[0, 0].axis('off')
29
30axes[0, 1].imshow(result_brightness, cmap='gray')
31axes[0, 1].set_title("Понижение яркости")
32axes[0, 1].axis('off')
33
34axes[1, 0].imshow(result_inversion, cmap='gray')
35axes[1, 0].set_title("Инверсия изображения")
36axes[1, 0].axis('off')
37
38axes[1, 1].imshow(result_threshold, cmap='gray')
39axes[1, 1].set_title("Пороговая фильтрация")
40axes[1, 1].axis('off')
41
42plt.subplots_adjust(wspace=-0.35, hspace=0.1)
43plt.show()

Как видите, матрицы — это мощный инструмент не только для чисто теоретических преобразований в линейной алгебре, но и для прикладных задач анализа данных и машинного обучения.
В каждой задаче, где нужно компактно описать и эффективно обработать многомерные данные, матрицы позволяют переводить реальную постановку в форму линейного или нелинейного уравнения.
В следующем параграфе мы обсудим, как с помощью матриц формулируются системы линейных уравнений и почему умение эффективно их решать столь важно для построения современных моделей машинного обучения и анализа больших датасетов.
А пока советуем пройти квиз.
